细辨差异求概率

姜华

我们可以通过列表法或画树状图法不重复、不遗漏地列出所有等可能发生的结果。概率问题看似很简单，其实并非如此，如果不认真审题，稍不留神就会出错。

易错警示1：对基本事件的理解有误

例1 大双、小双的妈妈申购到一张进博会的门票，兄弟俩决定分别用标有数字且除数字以外没有其他任何区别的小球，设计这样一种游戏确定谁去：口袋中放着分别标有数字1、2、3的三个小球，且已搅匀，大双、小双依次蒙上眼睛有放回地摸1次，大双摸到偶数就记2分，摸到奇数记0分;小双摸到奇数就记1分，摸到偶数记0分，积分多的就得到门票（若积分相同，则重复第二次）。请问这个游戏方案对双方是否公平？

【错解】P（大双摸到偶数）=1/3，积分为1/3×2=2/3;P（小双摸到奇数）=2/3，积分为2/3×1=2/3。

所以这个游戏方案对双方都公平。

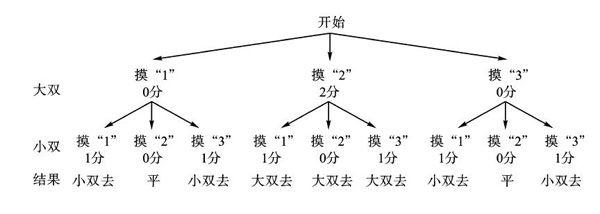
【分析】可能出现的所有等可能结果列树状图如下：

【正解】这个游戏方案不公平。P（大双去）=1/3，P（小双去）=4/9，所以这个游戏方案对小双有利。

易错警示2：未能区分放回与不放回

例2 一个不透明的盒子中放入四张卡片，每张卡片上都写有一个数字，分别是-2，-1，0，1，卡片除数字不同外其他均相同。从中随机抽取两张卡片，抽取的两张卡片上数字之积为负数的概率是（ ）。

A.1/4 B.1/3 C.1/2 D.3/4

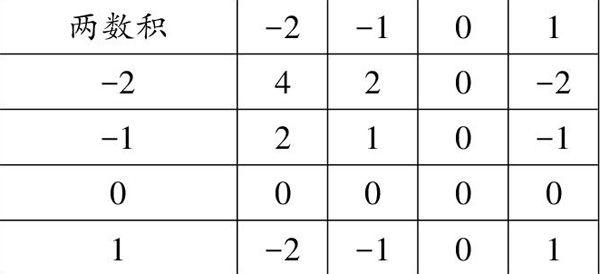
【错解】列表如下图，故所抽取两数的积为负数的概率为4/16=1/4，选A。

【分析】从中随机抽取两张卡片，相当于先后抽两次，第一次抽过后不放回，再抽第二次。需要注意区分的是：抽卡片、扑克牌，摸袋中球等要看清题目条件的叙述是“有放回”还是“无放回”。对于“无放回”，一是题目条件中交代是无放回，二是同时抽两张暗示无放回;“掷骰子”“抛硬币”“摇转盘”只有一种，第一次出现的，第二次还有可能出现，相当于“抽”“摸”中的有放回。

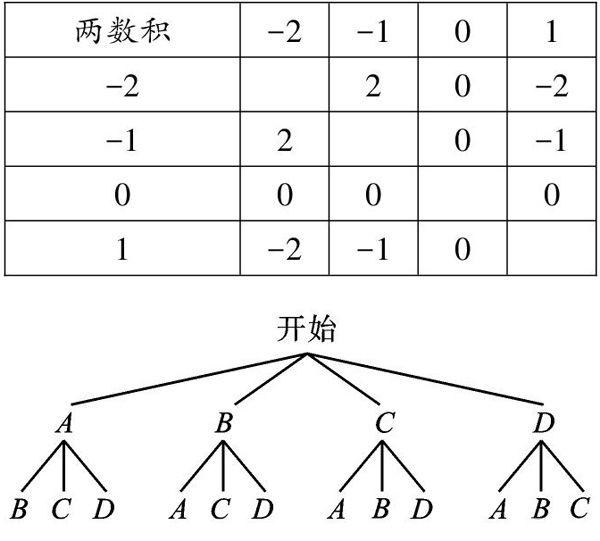
【正解】列表如圖，故所抽取两数的积为负数的概率为4/12=1/3。选B。

易错警示3：思考不周有遗漏

例3 某单位A、B、C、D四人随机分成两组赴北京、上海学习，每组两人。求A、B分在同一组的概率。

【错解】根据题意画树状图得：

共有12种等可能结果，A、B分在同一组的结果有两种，因此P（A、B分在同一组）=2/12=1/6。

【分析】树状图画得不错，共有12种等可能结果也不错，错在考虑问题不细致。树状图中，当C、D分在同一组时，意味着A、B分在另一组，A、B在另一组也是分在同一组，因此错解遗漏了这两种等可能结果。

【正解】根据题意画树状图得：

由树状图共有12种等可能结果，列表如下：

由表格中的12种方案知：A、B分在同一组有4种方案，分别是方案1、4、9、12，

所以P（A、B分在同一组）=4/12=1/3。

【点评】我们根据题意画出树状图后，切不可急不可耐地去求概率，应放慢脚步，写出所有等可能结果，认真看清楚题目要求，读懂每一句话的含义，从中找出所求事件的结果数。如本题在画树状图时，不能忘记树状图中没有出现的A、B被分在另一组的情况。