领悟统计思想 正确估算总体

徐向荣

我们从总体中抽取样本是为了认识总体，通过抽样调查了解总体的情况。用样本估计总体是一种重要的数学思想。通过对数据的分析，根据统计结果，我们可以做出合理的判断和预测。

一、用样本的平均数和中位数分析总体

例1 下表是随机抽取的某公司部分员工的月收入资料。

（1）请计算以上样本的平均数和中位数：

（2）甲、乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平，请你写出甲、乙两人的推断结论;

（3）指出谁的推断比较科学合理，能真实地反映公司全体员工月收入水平，并说出另一个人的推断依据不能真实反映公司全体员工月收入水平的原因。

【分析】（1）根据平均数、中位数的定义即可求解;

（2）甲、乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平，根据（1）中的结论可直接写出;

（3）乙的推断比较科学合理，用平均数来推断公司员工的月收入易受极端值影响。

解：（1）样本平均数=1/26×（45000+18000+10000+5500×3+5000×6+3400+3000×11+2000×2）=6150（元），中位数：3400+3000/2=3200（元）。

（2）甲：由样本平均数6150元，估计全体员工月平均收入大约为6150元。乙：由样本中位数为3200元，估计全体员工中大约有一半的员工月收入超过3200元，有一半的员工月收入不足3200元。

（3）乙的推断比较科学合理，用平均数来推断公司员工的月收入易受极端值45000的影响，这里只有3个工人的月收入超过平均水平。

二、用样本的频数分布状况分析总体

例2 为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下（成绩得分均为整数）：

根据表中提供的信息解答下列问题：

（1）频数分布表中的a=__，b=__，C=__;

（2）已知全区八年级共有200个班（平均每班40人），用这份试卷检测，108分及以上為优秀，预计优秀的人数约为

，72分及以上为及格，预计及格的人数约为__，及格的百分比约为__：

（3）补充完整频数分布直方图。

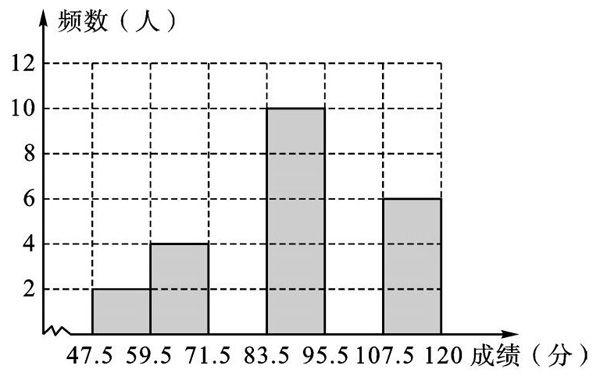
某班数学成缩分布盲方图

【分析】（1）由第一组的频数和频率，结合频率=频数/总数，可求出总数，继而可分别得出a、b、c的值;

（2）首先明确样本中优秀的频率、及格的频率和及格的百分比，然后利用样本估计总体的思想，根据频率=频数/总数的关系分别求出总体中优秀的人数、及格的人数、及格的百分比;

（3）根据（1）中a、b的值即可补全图形。

解：（1）∵被调查的总人数=2÷0.05=40（人），

∴a=40×0.2=8，b=40-（2+4+8+10+6）=10，c=10÷40=0.25。

（2）预计优秀的人数约为200×0.15×40=1200（人），

预计及格的人数约为200×（0.2+0.25+0.25+0.15）×40=6800（人），

及格的百分比约为（0.2+0.25+0.25+0.15）×100%=85%。

（3）补全频数分布直方图如下：

在统计里，我们通常从总体中抽取一个样本，通过研究样本的某些特性（如平均数、众数等）来估计总体的相应特性，这种用样本估计总体的方法是行之有效的，有一定的科学性。但同时我们需要注意的是：为了获取较为准确的调查结果，抽样时要注意样本的代表性和广泛性。