复合材料层合板应力分析逐层辛元法

刘艳红，张 正

（中国民航大学航空工程学院，天津 300300）

由于复合材料层合板的各向异性，在工程结构设计中准确地确定这类结构在载荷作用下的应力值至关重要。复合材料层合板的精确解[1-2]只适应于简单载荷、简单几何形状和简单边界条件，为解决工程实际中各种复杂问题，研究人员提出了不同的有限元法。传统位移有限元法可较准确地预测位移、面内应力和面外应力中的法向应力，但面外应力中两个横向剪切应力的预测结果精度较差[3-4]。

通常情况下，基于逐层理论的位移有限元的精度比传统的位移有限元法的精度更好[5-7]。但位移有限元法的应力结果是通过位移的解得到的，基于逐层理论[5]的位移有限元法很难满足层间面外应力的连续性。部分杂交应力元[8]通过假设面外应力变量建立单元刚度矩阵。尽管部分杂交应力元可以减少传统杂交应力元的计算量，但其结果精度仍然取决于面外应力场的选择。此外，这类部分杂交应力元的刚度矩阵计算涉及到单元矩阵的求逆运算，比较耗时。

基于修正的H-R 变分原理，文献[9-10]提出了部分混合元法，其中包括全部位移变量和面外应力的2个横向剪应力变量，这2 类变量采用了相同的插值函数。因此，面外应力的2 个横向剪应力可以直接求解，其他应力按位移有限元模型进行计算。此类部分混合元能够满足层合板界面2 个横向剪切应力的连续性要求和上下表面横向剪切应力的边界条件，这2 个应力结果精度较高，但不包含法向应力变量，无法保证界面间法向应力的连续性。

根据修正的H-R 的混合变分原理，文献[11]提出了一种8 结点非协调混合元，其单元列式中包含了3个位移变量和3 个面外应力变量。其中，3 个位移变量采用了非协调的插值函数。基于该单元的模型可同时求解位移和全部面外应力，且在网格划分较稀疏的情况下结点的面外应力精度高。

在辛元方法[11-12]基础上，基于逐层理论给出辛元两类变量的插值函数，推导逐层辛元列式并进行数值验证。

1 基础理论

1.1 势能原理

忽略结构的体积力，且假设位移边界u-u¯=0，则势能原理可表示为

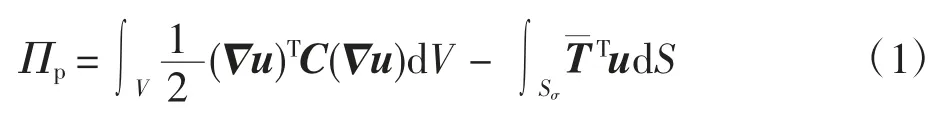
其中：u=[u1u2u3]T为位移向量；Δ为微分操作矩阵；C为材料矩阵；V 为体积；S 为表面积；为作用在Sσ上已知的表面力。

1.2 修正的H-R 变分原理

修正的H-R 变分原理[12-15]可表达为

其中，LM为Reissner’s 能密度函数，即

其中：σo=[σ13σ23σ33]T为面外应力；Φ11、Φ21和Φ22为材料参数矩阵；Δ1、Δ2和Δ3为算子矩阵。

面内应力可由面外应力与位移表示，即

其中，σi=[σ11σ22σ12]T。

2 逐层辛元插值函数

2.1 位移场插值函数

Reddy 等[5]提出了可分离插值函数的逐层单元，如图1所示。

位移场插值函数为

图1 逐层元Fig.1 Layerwise element

其中：u1j，u2j，u3j表示结点3 个方向的位移；n 为厚度方向的结点数。如图1所示，厚度方向子层数为Ne=（n-1）/2，厚度方向的全局插值函数Hj（x3）可表示为

其中：k=1，2，…，Ne；hk为第k 层的厚度；表示第k 层的底部坐标。对应式（6）的等参形式为

根据式（7），可直接给出3 个位移变量插值函数表达式，即

其中，Ni为平面内的等参插值函数，即

其中：ξ0=ξiξ，η0=ηiη（i=1，2，…，8），ξi和ηi为结点i的局部坐标。

2.2 面外应力插值函数

与文献[11-12]中辛元方法的思想相同，面外应力的插值函数与位移的插值函数相同，即

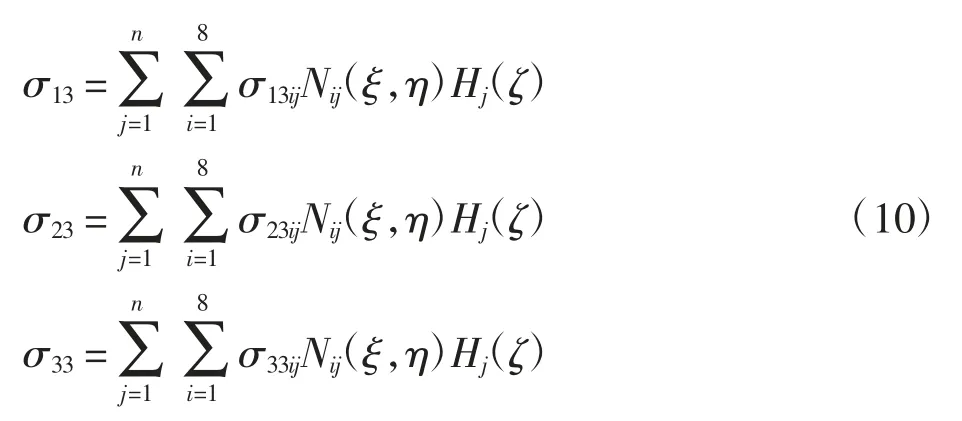
3 逐层辛元列式推导

3.1 位移元子层列式

将式（8）代入式（1）中，考虑位移的变分，则位移元子层的列式为

其中：qe=[u1eu2eu3e]T表示子层结点的位移向量；Dqq=，这里的N 代表子层的等参插值函数矩阵。

3.2 逐层辛元子层列式

将式（8）和式（11）同时代入式（2）中，可得修正的H-R 变分原理的离散形式为

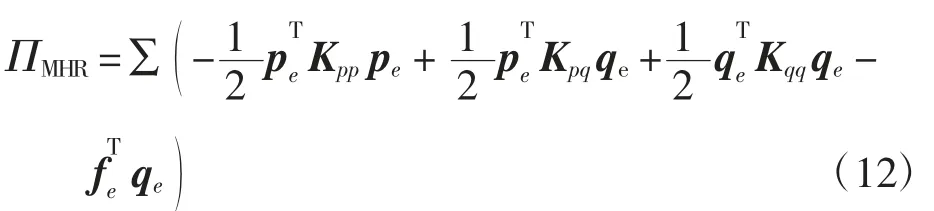
其中，pe=[σ13eσ23eσ33e]T为子层结点的面外应力向量，fe的积分式与式（11）中fe的积分式相同，另外有

将pe和qe视为相互独立的变量，由δΠMHR（pe，qe）=0 可得逐层辛元子层的列式为

需要说明：式（13）中Kqq的主对角线上含有0元素（由于微分算子矩阵Δ2的主对角线上有0 元素）。实践表明，与传统的混合元一样，如果简单用式（13）求和后所得到的控制方程来求解具体问题，位移和应力结果并不随网格的增加而稳定收敛。

为了消去式（13）中主对角线上的0 元素，将其与式（11）合并，则有

其中，Rqq=Kqq+Dqq。

交换上式的行并变形，可得

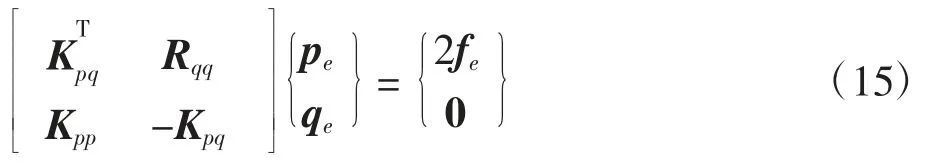
显然，式（15）的形式与文献[14-15]中非协调辛元完全相同，满足辛空间Hamiltonian 矩阵的定义，因此，这里称式（15）为等参形式的逐层辛元子层列式。

3.3 逐层辛元列式

根据逐层元中各子层共用结点的关系，对式（15）求和可得到逐层辛元列式，即

将所有单元的式（16）叠加且交换行后，则结构的整体线性系统为

其中，K11=-∑Kpp，K12=∑Kpq，K22=∑Rqq，f=2∑fe，q=∑qe，p=∑pe。

4 数值算例

4.1 收敛性分析

考虑3 层的层合板[0°/90°/0°]，几何尺寸b=a=1.0，总厚度h=1.0，每层厚度相同。边界条件：在x1=0和x1=a 处，σ11=u2=u3=0；在x2=0 和x2=b 处，σ22=u1= u3= 0。假设上表面施加垂直向下载荷p = q0×sin（πx1/a）sin（πx2/b），下表面3 个面外应力分量为0。材料参数为：E11= 25E22= 25E33，G12= G13= 0.5E33，G23=0.2E33，μ12=μ13=μ23=0.25。

逐层辛元收敛情况如图2所示，其中，横坐标为有限元模型的网格划分情况：2 表示2 × 2 × 12；3 表示3×3×12，依此类推。图中给出的误差为12×12×12 模型与精确解的误差，即

其中：Present 为逐层辛元解；Exact 为由文献[2]方法给出的精确解。

可以看出，逐层辛元的结果收敛情况良好。当有限元模型网格划分为12×12×12 时，各类变量的结果接近精确解。

4.2 应力分析

图2 逐层辛元收敛速度Fig.2 Convergence rate of layenise symplectic element

图3 各参数沿厚度方向的分布Fig.3 Parameter distribution along thickness direction

各变量沿厚度方向的变化趋势如图3所示。图中应力结果是根据材料的本构关系计算所得高斯点应力，然后用外推方法得到结点上的应力，最后对相邻单元同一个结点应力值取平均值得到。图3（d）～图3（i）中各应力分量的结果采用如下无量纲公式，即

其中：q0表示载荷；S 表示长厚比，S=a/H=10。

网格模型相同的情况下，图3（a）～图3（c）表明，8结点非协调位移元（NC3D8）、逐层辛元的位移结果与精确解的精度相差不大。非协调位移元的结果更贴近精确解，但逐层辛元结果的最大误差仅为0.504%。图3（d）～图3（f）表明，逐层辛元的面外应力和的结果比非协调位移元更接近精确解。图3（g）～图3（i）表明，两个面内法向应力和沿厚度方向的非线性分布特性并不显著，两种方法的精度基本一致。

5 结语

1）在推导逐层辛元的列式时，其面外应力变量和位移变分量采用相同的逐层插值函数，缺少非协调项的消去过程，与文献[14-15]中建立8 结点非协调辛元的过程比较，推导过程简便；

2）联合最小势能原理和H-R 变分原理所建立的逐层辛元列式系数矩阵对角线没有0 元素，故对应线性系统的解稳定可靠；

3）逐层辛元有限元线性系统包含位移和面外应力两类变量，便于引入面外应力边界条件。因此，逐层辛元面外应力和非协调位移法相应变量的结果更贴近精确解。