跨声速空腔声学特性数值模拟

马丽璇，李恩义，孙书霞，杨庆祥

（安阳工学院飞行学院，河南 安阳 455000）

在航空应用领域中，空腔流动是空气动力学的研究热点之一，例如飞机起落架舱和飞行器武器舱等。当高速气流流经空腔时，空腔外部剪切流与内部流动相互作用，经常会出现自持振荡现象，会产生剧烈的压力、速度脉动，进而引发强烈的噪声。该问题涉及到流体动力学中的非定常分离流、自由剪切层的不稳定性、涡动力学、湍流剪切层中相干结构（拟序结构）、声与流动的相互作用等前沿问题。对于武器舱来说，高于170 dB 的压力脉动可能会损害飞行器结构和导弹及防碍导弹的正常分离。

对于空腔流动，相关学者已进行了大量理论分析、实验测量和数值计算。Rossiter[1]引入边缘声调分析理论并推导出用于估算空腔流场自持振荡频率的半经验公式，即著名的Rossiter 半经验公式。随着技术发展，大量先进的非接触式高精度测量方法[2-3]应用于空腔流动中，如粒子图像速度场仪（PIV）、激光多普勒测速仪（LDV）。由于流激噪声在流场和声场的长度、尺度存在巨大不一致性，准确计算声场特性具有一定难度。在低雷诺数瞬态粘性流场中采用直接数值模拟（DNS）[4-5]是可行的，但对于高雷诺数流动则不可行，工程实践中多采用雷诺平均N-S 方法、大涡模拟方法（LES）、混合RANS/LES 方法。Temmerman 等[6]采用URANS 方法分析了均流和单音模态及时间步长对噪声预测的影响。Aybay 等[7]采用LES 方法研究了湍流流场空腔近场噪声，并将计算结果同实验值和高精度格式计算值进行了对比分析。Peng[8]采用分离涡模拟（DES）方法研究了空腔内压力脉动和流经空腔上方的混合层及腔内涡运动对后壁附近混合层的影响。王显圣等[9]对空腔可压缩流致噪声问题的研究进展进行综述，分析空腔流激振荡及其产生噪声的机制、参数影响规律与噪声控制技术发展趋势。刘瑜等[10]使用延迟分离涡模拟方法研究了来流马赫数为0.85 的矩形开放腔体气动声学环境。余培汛等[11]基于耦合湍流速度生成模型与线化欧拉方程，建立了气动噪声混合预测方法，对空腔标模M219 的气动噪声进行了预测。

为改善空腔流场内的声学环境，可采用一些措施对流场进行控制，常用方法包括：主动控制和被动控制，如几何修型、底部泄压管、前缘立齿、前缘射流。Bastrzyk 等[12]通过在空腔前缘位置处放置圆杆来削减剪切层，达到降低噪声的目的，并考虑了不同圆杆位置的降噪效果。Lada 等[13]通过分析3 种不同微射流速度工况，得出射流改变了剪切层的稳定性和空腔内的反馈回路，可实现降噪及减小腔内阻力。Soemarwoto 等[14]分析两种不同几何形状工况，得出修形后可使谐振频率增大但振幅减小。Wilcox 等[15]通过在空腔底板开泄压腔，使空腔后部的高压区向前部的低压区流动，从而达到平衡压力的目的，进而有效地改善空腔流场特性。Ukeiley 等[16]采用在空腔前缘添加立齿的方法对空腔流动进行控制，结果表明仅将空腔前缘边界层抬高并不能很好地降低腔内噪声。吴继飞等[17]在高速风洞中对空腔流场气动声学特性进行实验研究，对空腔后壁进行倒角，以降低气流在该处的撞击强度，从而达到抑制空腔流场气动噪声的目的。周方奇等[18]通过开展高速风洞实验研究跨超声速来流条件下前缘直板装置对空腔（长深比为6）流动和噪声的控制机理，通过对比多种前缘直板控制条件下的腔内噪声声压级分布，确定直板控制参数的优化选择方法及最优参数；利用静态／动态压力传感器和油流实验采集腔内静压、脉动压力和壁面流谱，着重分析前缘直板对腔内流动结构、声压级和声压频谱的影响规律。张群峰等[19]利用基于SST k-ω 湍流模型的改进延迟分离涡模拟方法，对开式空腔气动声学特性进行数值模拟研究，在腔体尾缘采用后壁开孔板加耗能腔的方法进行流动控制。

由于声波频率范围很宽，高频和低频的声波波长尺度相差很大，为能捕捉到最大频率波，要求声场计算网格要很密，时间步长取值要很小，声场的计算时间较长。上述研究中，为取得良好的噪声数值模拟结果，大多都采用DES 或LES 湍流模型，甚至于DNS 模型，所需计算网格分辨率要求高，数值计算代价大，不利于工程实践应用。为此，提出一种基于CFD/CAA 方法来求解声学信息，即Cubic k-ω 湍流模型结合非线性声学求解器方法（NLAS, nonliner acoustic solver）。首先，通过与实验对比验证了该方法的有效性。然后，为了降低噪声，对比分析了4 种不同构型，得到最优结构，该方法减少了网格需求量且精度较高，有利于工程实践应用。

1 数值计算方法

1.1 湍流方程

采用Cubic k-ω 湍流模型[20]，其湍动能k 和耗散率ε 的输运方程为

其中：ρ 为流体密度；t 为时间；ui为速度在i 方向上的分量；xi为笛卡尔坐标系下i 方向的位移；Tt为时间尺度；μ 为粘度，μt为涡粘度；Pk为速度梯度产生的湍动能；E 为内能；常量Cε1=1.44，Cε2=1.92，σk=1.0，σε=1.3。

1.2 非线性声学求解器

小尺度湍流运动产生的噪声源在一定程度上可较好地模拟。然而，对于影响相干拟序结构或辐射噪声的大尺度结构模拟不太理想，对此Batten 等[21]提出了非线性声学求解器的基本原理。

NLAS 计算噪声的产生和传播基于初始的统计稳态湍流，数据可由传统的RANS 模型提供。初始步提供了平均流场基本特征和强制设定的湍流脉动统计描述。NLAS 通过对统计结果的重构获得噪声源来模拟压力脉动传播。

其中

其中

式中，cp为定压比热容。

NLAS 可以运行由原始RANS 计算结果截断得到减小的子域，截断的边界被定义为远场吸收边界。该边界不仅提供湍流统计，还可以提供变化的平均场数据，且外边界更接近能表现流场重要特征的区域。此外，还可以进一步放宽对网格的要求。这是因为稳态RANS 解可以插值到用于后续瞬态模拟中较粗糙的网格。所以，非线性声学计算求解器在求解时对网格的需求较小，与DNS、LES、Hybird RANS/LES 的需求量对比如图1所示。

1.3 湍流人工重构

图1 DNS、LES、Hybird RANS/LES、NLAS 所需近壁网格分辨率Fig.1 Required near-wall mesh resolutions with DNS,LES,Hybrid RANS/LES and NLAS

在NLAS 方法中，大尺度脉动可被直接描述；对于小尺度压力脉动采用人工重构方法。Smirnov 等[22]基于雷诺应力张量的相似变换张量嵌入尺度概念，使其成功的应用于各向异性湍流中。傅里叶模式方程[23]如下

其中：αik为应力张量的Cholesky 分解；n 为模态阶数；N 为阶数上限；pni和qni分别为余弦和正弦的系数；ω 为湍流频率；di为波矢。

2 NLAS 方法验证

2.1 几何模型

验证算例采用文献[24]中的M219 矩形开式空腔，其尺寸长：宽：深（L：W：D）=5：1：1，空腔深为0.101 6 m，在空腔底部设有10 个压力传感器（K20～K29），如图2所示。计算域：进口到空腔前缘的距离是7.75 D，空腔尾缘到出口的距离是5.25 D，空腔开口到顶部边界的距离是17 D，两侧边到空腔的距离均为1 D，如图3所示,其中箭头为自由来流方向。

图2 空腔结构及传感器位置Fig.2 Cavity structure and sensor location

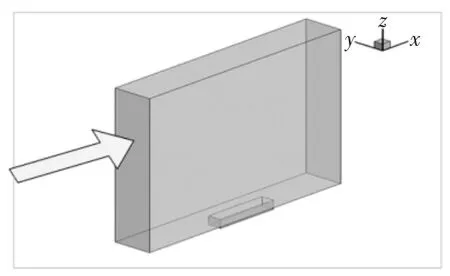
图3 空腔流动计算域Fig.3 Calculation domain of cavity flow

2.2 边界条件和求解方法

自由来流流动条件为：马赫数Ma∞=0.85，静压P∞=62 096 Pa，静温T∞=266.53 K，基于空腔长度的雷诺数Re=6.8×106。对于流动边界，进口施加1 个稳态湍流边界层，在空腔前缘的边界层厚度为0.37×Re-0.2，即10.16 mm；空腔壁面采用绝热无滑移壁面；其余为基于流动特征的边界并设置3 层远场吸收层。对于声学边界，外部来流设为NLAS 外部边界并设置3 层远场吸收层，以抑制声波在远场边界反射；空腔壁面采用绝热无滑移壁面。

基于有限体积法离散控制方程，空间离散采用具有二阶精度的TVD 格式，TVD 限制器为Min-mod，时间积分采用双时间步长隐式方法。同时采用多重网格法加速收敛和并行计算减小计算代价。时间步长Δt=2×10-5s，共计算20 000 步，考虑到压力的时间序列和时间均化，为获得平均流动特性将前5 000 步数据舍弃。

2.3 M219 空腔声学预测

空腔噪声的主要特征：空腔开口处混合层的不稳定性和空腔内部瞬态涡运动。不稳定性是由于剪切层与空腔后部壁面碰撞造成自持振动。在文献[24]实验中，测量了空腔底部10 个位置（K20～K29）的压力脉动，其被均匀地分布在空腔底部X/L=0.05 ～0.95 位置上。

功率谱密度（PSD）无法直接测得，可通过Burg 方法将采样压力脉动转化为功率谱密度，而声压级(SPL)可通过功率谱密度计算得到，即

其中，pref=2×10-5Pa 是最小可听声压，也是基准声压。

图4分别给出了位置点K20、K22、K29的计算声压级，对比实验数据，NLAS 方法可与其很好地吻合，验证了该方法在求解气动噪声的合理性。在图5中，SADES[25]和NLAS 方法计算所得功率谱密度幅值大部分情况下均大于实验值，可知两种方法对压力脉动的预测有些偏高。此外，SA-DES 方法求解获得曲线较平滑，NLAS 方法求解获得曲线的波动较大，可见NLAS方法能更好地捕捉到压力脉动。

谐振频率可用Rossiter 经验关系式评估

其中：U∞和M∞分别为自由来流速度和马赫数；γ 为压力波与空腔尾缘碰撞后产生的相位移，取0.29；L 为空腔长度，α 和κ 分别为相位延迟量和对流涡与自由流流速比，κ 取0.57。基于Rossiter 公式，Larcheveque 等[26]提出，诱导谐振与混合层涡在下游的移动速度和压力波在空腔上游声速相关。

图4 空腔底部K20、K22、K29 位置点的声压级对比Fig.4 SPL comparison at locations K20，K22 and K29 on cavity floor

表1给出了K29处模态频率的实验值、Rossiter 公式估算值、4 阶高精度格式算值[27]和NLAS 计算值。将NLAS 方法计算所得的1～4 阶模态频率与实验值对比，可知1 阶、2 阶、4 阶模态频率略高于实验值且误差分别为2.6%、3.2%和2.7%，3 阶模态频率与实验值吻合良好，误差仅为0.3%。然而，4 阶高精度格式的1 ～3阶模态频率计算值均偏低和4 阶模态频率偏高，误差分别为-13.2%、-10.3%、-8.6%和2.7%。可知，NLAS 方法可以很好地预测空腔噪声的模态频率。

表1 K29 处的模态频率对比Tab.1 Modal frequency comparison at K29

3 被动控制

为抑制空腔噪声，改善空腔流场环境，采取3 种不同结构：①前缘壁面改为45°斜边（Case 1）；②尾缘壁面改为45°斜边（Case 2）；③前缘和尾缘壁面均改为45°斜边（Case 3）。对于初始模型算例标记为Original。

图6给出了K20、K22、K293 个位置点4 种工况下的声压级对比。可以看出，在Case 2、Case 3 工况下，声压级有所下降，实现降噪目的。对于Case 1 工况下，特别是空腔中部（K22），其声压级有所增大，未实现降噪目的。对于Case 3 来说，由于具有Case 1、Case 2 的构型，因而一方面实现了降噪目的，另一方面又增大了空腔中部压力脉动，使空腔中部声压级提高。此外还使其几何结构变得复杂，不利于机械加工。造成这种现象的原因是，由于前缘斜壁改变了气流方向，自由剪切层向空腔底部移动，造成压力脉动增大；尾缘斜壁使剪切层对空腔后壁的撞击减缓，进而使压力脉动减小，声压级降低。

时间平均总声压级计算如下

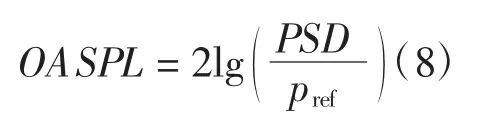
由图7对比实验值和NLAS 计算值（Original）可知，从K20到K21测量点总声压级稍微下降，然后沿着流动方向（从K21到K29）总声压级增大，即压力脉动增大。实验值与计算值趋势一致，且计算值相比实验值被过高预测约5 dB。

由于湍流剪切层的Kelvin-Helmholtz 不稳定性会产生多种不稳定性现象，如旋涡的破碎和运动涡核等[28]。为更好地显示旋涡特征，可采用准则方法[29]。根据Hunt 理论，如果涡张量对流体变形的贡献大于应变率张量认为该区域有涡存在，准则定义如下

其中：Sij和Ωij分别为Δu 的对称分量和反对称分量。根据速度梯度张量具有广义Galilean 不变性，可知其值与坐标系的选取无关。Q>0 时表示有涡存在，等值面包围的区域定义了一个涡核，反之则无。图8给出了4种结构下空腔附近流场旋涡结构（Q 准则）。Powell[30]和Howell[31]从涡动力学角度考虑流体发声机理，建立涡声理论，认为气动噪声主要源于流场中涡系的拉伸与破裂。后缘斜面起到涡流发生器的作用。

图6 4 种工况下空腔底部K20、K22、K29 位置点的声压级对比Fig.6 SPL comparison at locations K20,K22,and K29 on cavity floor under four conditions

图7 沿空腔底部总声压级Fig.7 OASPL comparison along cavity floor

由于涡结构图不能直观的表示噪声的大小，故引入VLamb的模。图9为不同结构下的VLamb模大小对比图，其中VLamb=u×Ω，即速度叉乘以涡量，其可以反映声源的大小。结合上述分析，由图可知：①对于Original 结构，剪切层脱落涡撞击空腔尾缘壁面产生一次声波并向前传播至前缘，引起剪切层扰动，造成二次声波以及涡脱落，完成1 个反馈回路，进而形成自持振荡；②对于Case 1 结构，结合图5可知，由于前缘壁面变为倾斜使气流方向改变，造成空腔中部压力脉动增强，噪声增大；③对于Case 2 结构，由于尾缘壁面变为倾斜，降低了壁面对一次声波的反射，进而降低了二次声波的辐射，实现了降低噪声的目的；④对于Case 3 结构，由于前、尾缘壁面均变为倾斜，使其一方面降低了一次声波反射，减小了噪声，另一方面空腔中部压力脉动增大，噪声变大。此外，当采用斜壁面时，增大了空腔的长度，使空腔流场特性由开式向闭式过度。

图8 湍流结构等值面（Q ＝7×106）Fig.8 Iso-surface of turbulence structure（Q ＝7×106）

图9 不同构型VLamb 的模大小Fig.9 Magnitude of VLamb with different configurations

4 结语

基于CFD/CAA 方法对三维可压缩开式跨声速空腔M219 进行了数值分析可知，声压级风洞实验值与数值计算值可以很好地吻合；对比风洞实验值、NLAS 和SA-DES 计算值的功率谱密度，可知NLAS 方法可更好地捕捉到压力脉动；分析对比Rossiter 经验关系式、4 阶高精度格式与实验值的模态频率的误差率；验证了非线性噪声求解器方法（NLAS）可以很好地预测空腔噪声。

采取被动控制措施几何修型以实现降低空腔气动噪声的目的，分析和对比4 种工况下，其声压级、总声压级、Q 准则等值面、Lamb 矢量。可知，前缘修型造成空腔中部压力脉动增大，噪声也随之增大；尾缘修型降低了壁面对一次声波的反射，进而降低了二次声波的辐射，实现了降低噪声的目的，即Case 2 降噪效果最好，大约降低5 dB，可应用在实际工程中。