基于航班网络的受扰航班一体化恢复模型

彭连锁，王梓旭，王兴隆

（1.中国国际航空股份有限公司，北京 100621；2.北京大兴国际机场，北京 102604；3.中国民航大学空中交通管理学院，天津 300300）

航空公司大面积受扰航班恢复包括分阶段恢复与一体化恢复。分阶段恢复是将整个恢复问题分为飞机恢复、机组恢复、旅客恢复3 个阶段逐步求解；一体化恢复则是综合考虑飞机、机组、旅客因素进行求解。两者相比，一体化恢复模型复杂度高、结果更准确。

Lettovsky[1]于1997年提出一体化恢复方案，包括机组人员、飞机、旅客流的一体化恢复，开辟了一体化恢复的先河。乐美龙等[2]综合考虑飞机、航班、机组和机场的动态时空衔接，建立了飞机和机组的优化恢复模型，并设计了一种GRASP 算法求解。朱博等[3]分析了飞机和机组运行计划的异同，建立了飞机和机组一体化恢复的约束规划模型，利用混合集合规划设计搜索算法求解。Bisaillon 等[4]设计大型邻域搜索方法求解飞机与旅客一体化恢复问题。Sinclair 等[5]认为在未来的研究应考虑解决较大实例的方案，例如将列生成算法嵌入滚动时间窗中，解决扰动次数更多的情况。Teodorovic 等[6-9]在先后使用分支定界、动态规划、启发式算法对旅客恢复和机组恢复问题进行了求解。吴刚等[10]提出一种改进列生成算法，每次迭代过程中加入多个列，并对加入的多个列需满足的条件进行了分析，算例验证了该方法的正确性和有效性。田倩楠等[11]改进了时空网络算法，给出占优准则，有效减少了可恢复航线的组合数量，提升了计算效率。

已有文献多采用时空网络进行建模，需考虑航班边、机场节点和时间节点，一体化模型过于复杂。Hanif等[12]系统介绍了航班网络的使用，所用算法相比时空网络模型复杂度低，但不能表现飞机维修约束、机组执勤时间约束、客票取消等时间和地点属性。Akturk等[13]在飞机恢复问题中首次使用巡航速度控制，并分析了该思路的优势。Ugur 等[14]基于此研究进一步将旅客行程加入模型，但均未达到真正的一体化恢复。

采用改进的航班网络进行问题建模，能够降低复杂度，并可避免航班网络不易表达飞机维修约束、机组执勤时间约束等属性类约束的缺陷[15]。

1 航班网络改进与算法设计

1.1 航班网络的改进

传统航班网络中包括3 类节点、3 类弧，改进航班网络中有4 类节点、5 类弧，新加入必经节点、必经弧和添加弧，如图1所示。

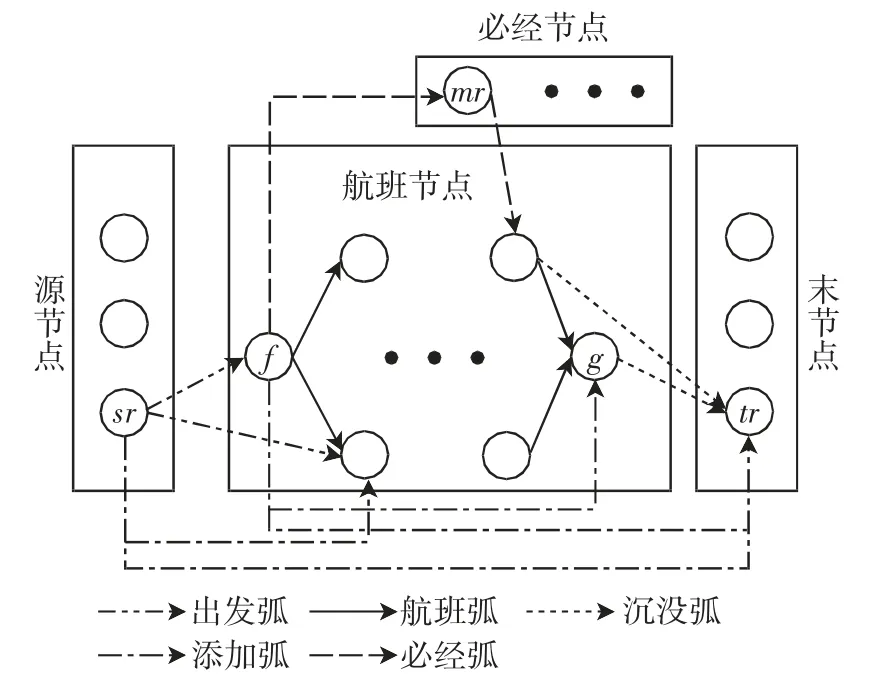
图1 改进后的航班网络Fig.1 Improved flight network

源节点（sr）表示飞机、机组或旅客的初始状态点，有时间、地点属性；

末节点（tr）表示飞机、机组或旅客的中止状态的点，有时间、地点属性；

航班节点表示飞机、机组执行的航班或旅客在其行程中要乘坐的航班；

必经节点（mr）表示飞机在特定时段在特定机场维修的节点，或机组规定在特定机场休息；

出发弧连接源节点与航班节点的弧，表示飞机、机组、旅客执行首个航班；

沉没弧连接航班节点与末节点的弧，表示飞机、机组、旅客执行完最后1 个航班；

航班弧航班节点之间的弧，表示飞机、机组、旅客执行完上游航班后执行下游航班；

必经弧连接航班节点与必经节点之间的弧，表示飞机维修、机组休息等；

添加弧表示航班恢复的特殊操作，如加机组、调机操作，乘客客票取消操作。

1.2 航班网络的算法设计

一体化恢复包含飞机、机组、旅客3 种子网络，用r 表示。算法参数及含义如表1所示。

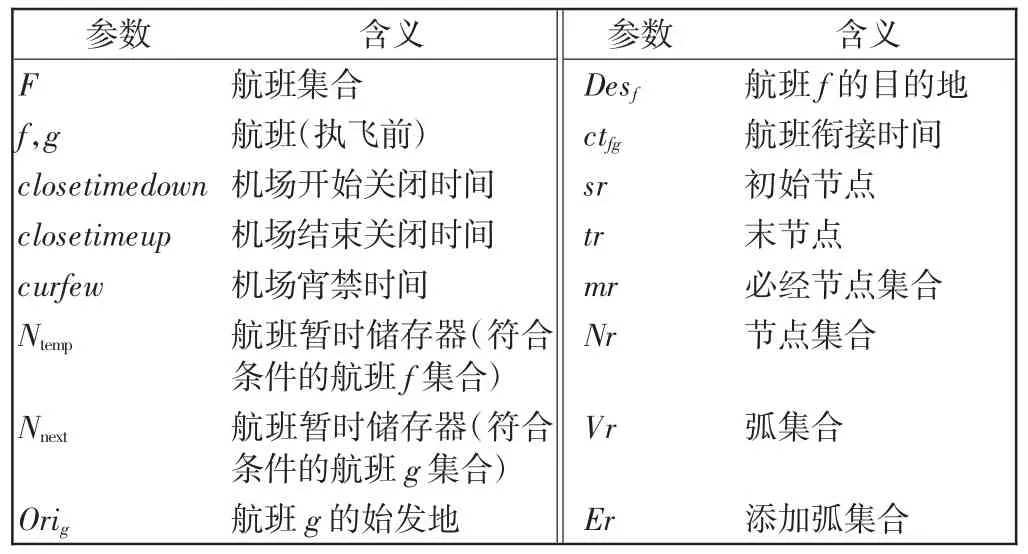
表1 算法参数及含义Tab.1 Algorithm parameter and meaning

航班网络生成算法由Generatesubnetwork（r），Generatepath（Ntemp），Insert（Ntemp）3 部分组成。具体步骤如下：

Step 1初始化节点集合Nr，弧集合Vr，Ntemp=sr；

Step 2Generatesubnetwork（r），航班网络生成主程序；

Step 3Generatepath（Ntemp），基于广度优先搜索可衔接航班，即航班网络路径中的节点；

Step 4Insert（Ntemp），得到航班网络中的所有弧与节点；

Step 5对Vr 进行分类得到出发弧、沉没弧、航班弧、必经弧、添加弧；对Nr 进行分类得到初始节点、航班节点、沉没节点；

Step 6如果是机组子网络，额外删除不满足机组执勤时间和飞行时间的弧与节点。

2 航班扰动一体化恢复模型

2.1 集合

F：航班集合，F = {f|f1，f2，…}，f 为任意1 个航班，|F|为航班总量；

R：飞机路径集合，R ={r|r1，r2，…}，r 为任意1个飞机路径，|R|为路径总数量；

A：飞机集合，A={a|a1，a2，…}，a 为任意1 架飞机，|A|为飞机总数量；

K：机组配对集合，K={k|k1，k2，…}，k 为任意机组配对，|K|为机组配对总数量；

C：机组集合，C={c|c1，c2，…}，c 为任意机组，|C|为机组配对总数量；

Q：旅客行程路径集合，Q={q|q1，q2，…}，q 为任意旅客行程路径，|Q|为路径总数量；

P：旅客行程集合，P={p|p1，p2，…}，p 为任意旅客行程，|P|为旅客行程总数量；

FC：联程航班对集合{f1，f2，f3}，f1、f2代表联程航班，f3表示联程航班拉直。

2.2 参数

参数及含义如表2所示。

表2 参数及含义Tab.2 Parameter and meaning

2.3 变量

模型将成本分解为航班延误运营成本、航班取消成本、旅客延误成本、旅客客票取消成本和机组空闲成本5 部分。中国民用航空局《航班延误经济补偿指导意见》规定，延误8 h 以上给出的赔偿标准接近于取消航班的赔偿，故令航班取消成本为航班延误8 h的运营成本；航班取消还导致旅客客票取消，这部分成本算为客票取消成本；模型中规定航班最多延误8 h，目标函数如式（1）～式（2）所示。

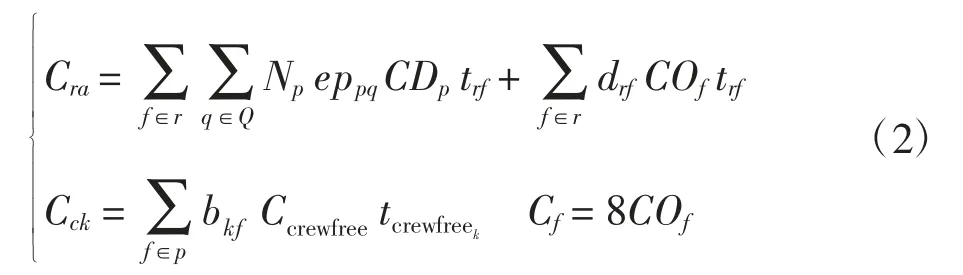
其中，epp为旅客行程p 分配给路径q 的人数比例。

在3 种航班网络中，飞机、机组两种网络需满足航班如果被执行则必然有飞机、机组执行该航班，否则航班被取消，称作航班覆盖约束，即

飞机与机组网络，从源节点到末节点只能执行1条路径，称作流平衡约束，如约束（5）与约束（6）。而旅客行程网络没有此约束，旅客行程可以将旅客分配到任一或多个旅客行程路径，或者取消行程，但是其人数和应等于该旅客行程人数，如约束（7）。一个航班如果被执行，则航班上被分配的各种行程的旅客人数之和不能大于执行该航班飞机的座位数，即

其中，cpp为旅客行程p 取消旅客人数比例。

将旅客分为普通旅客、中转旅客和联程旅客。令中转旅客最多中转1 次。图2为联程旅客在航班网络中的表示。

图2 联程航班在航班网络中的表示Fig.2 Connecting flights represented in flight network

联程航班如果两段都不取消，则两段必须使用同1 架飞机，并且继续联程；模型规定只有当中间机场出现问题时才可以进行联程拉直，否则两段飞行都被取消，即

飞机与机组的每1 个路径中的航班为满足限制条件都有不同的出发和到达时间，应满足机组最早可用时间比飞机的最早可用时间早，保证飞机可以起飞时一定有机组可以执飞，即

约束（11）表示取消行程旅客数为整数。约束（12）和（13）表示旅客行程p 分配给行程路径q 的旅客人数或取消人数比例小于1，约束（14）和约束（15）为变量的取值约束，即

3 DW 分解子问题设计

Dantzig-Wolfe（DW）分解算法是求解特定结构、不能使用标准单纯形法进行求解的大规模线性规划问题。由于该方法具有运行时间快、运算求解速率高等优点，故尝试运用该算法对模型进行求解。以顺延航班计划作为初始解构造增广约束矩阵，以路径变量表示的模型作为主问题，λi（i=1，2，…，8）分别对应约束（3）～约束（10）的对偶变量值。构建子问题的目的是不断发现简约成本为负的路线，子问题可分为飞机子问题、机组子问题、旅客子问题。算法参数及含义如表3所示。

表3 DW 算法参数及含义Tab.3 Parameters and meanings of DW algorithm

子问题可表示为

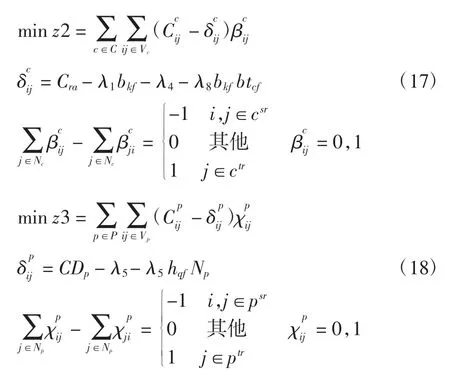
子问题求解过程是一个单源最短路问题。由于飞机、机组、旅客的航班网络结构稀疏，长度短，采用SPFA 算法求解子问题的最短路径，同时对路径包含的最多节点数进行限制，1 架飞机1 天最多执行的航班数设为6；1 个机组每天最多执行航班数设为4。模型求解流程如下：

Step 1根据顺延航班计划给出初始解构造主问题；

Step 2求解步骤1 得到的主问题，并返回约束的对偶变量λi（i=1，2，…，8）；

Step 3使用对偶变量分别修改飞机、机组、旅客子问题中的边的权值；

Step 4分别求解每个子问题当前边权值下的最小成本路径，将子问题的解以路径变量代入主问题求解其影子价格；

Step 5选择简约成本最小的路径，判断是否为负，若为负则加入主问题中继续求解，回到Step 3；否则问题已达到最优解。

其中，求解子问题最短路径SPFA 算法流程如下：

Step 1将子模型航班网络图中源节点sr 与每个节点f 之间的距离储存在路由表d（f），备用节点储存在先进先出队列Q 中，w（f，g）表示边（f，g）的权值；

Step 2遍历图中每个节点f，如果f≠sr，d（f）=∞；否则d（f）=0；

Step 3Q=Q∪sr；

Step 4如果Q 不是空集，删除其中第1 个节点f；

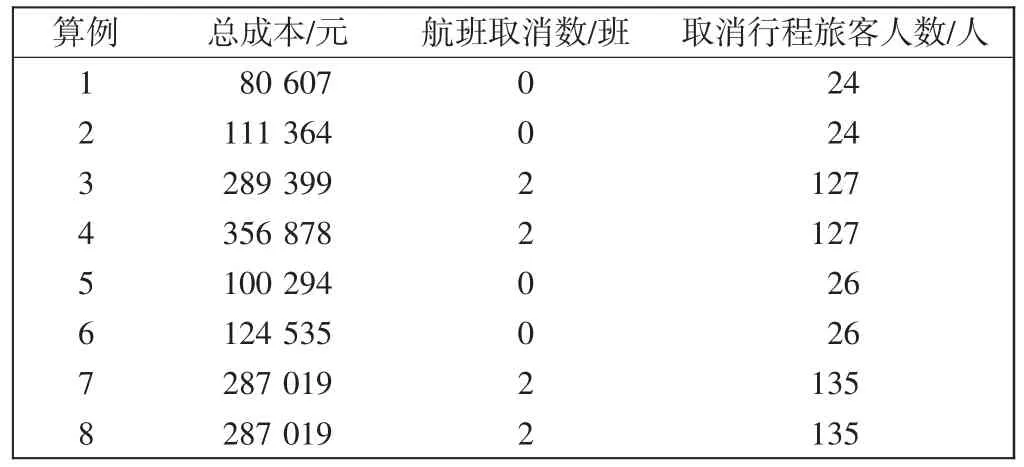
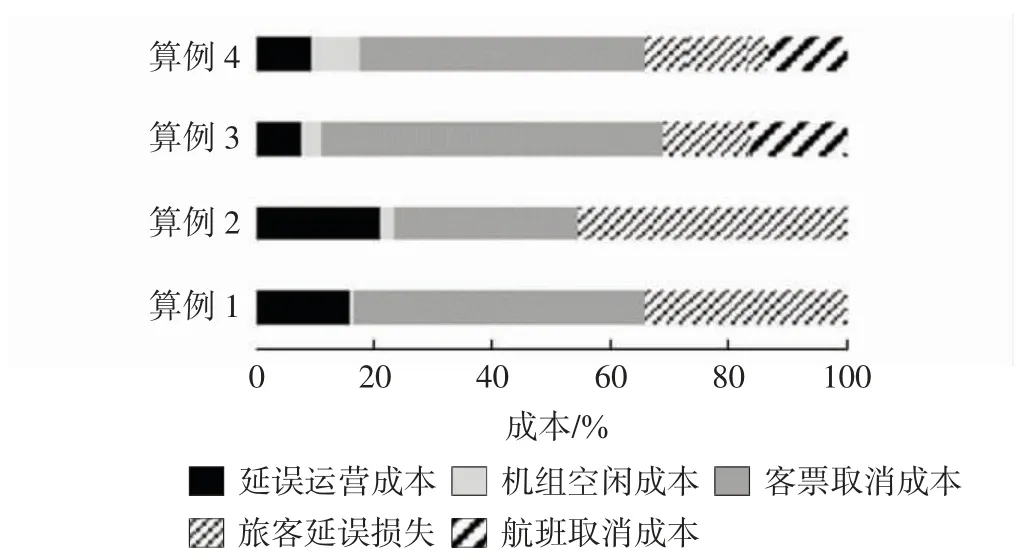
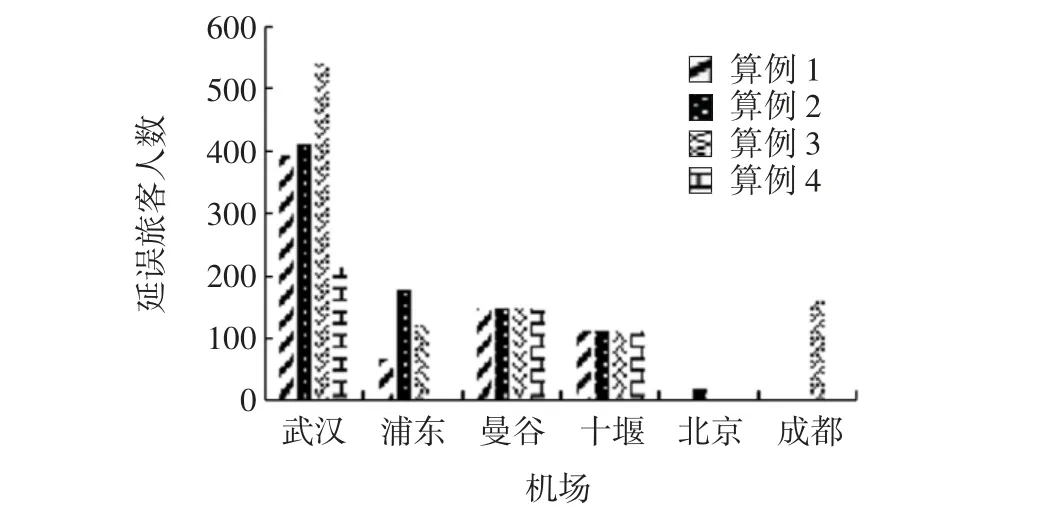
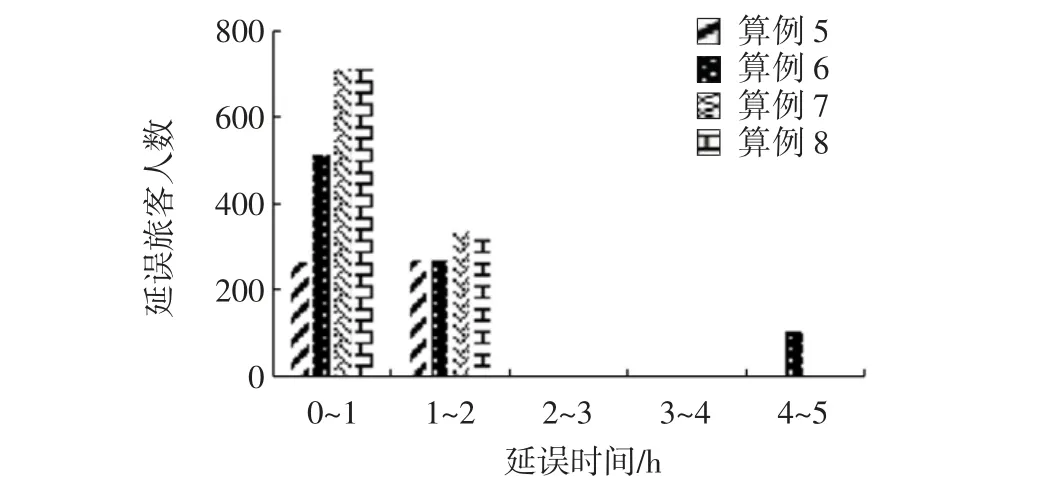
Step 5遍历所有从f 出发的边，如果d（f）+w（f，g）

Step 6转到Step 3，直到Q 为空。

4 算例分析

采用某航空公司一天的运营数据，构建两类共8个算例进行计算分析。包括机场关闭、飞机故障两种运营中最常见的场景，算例信息如表4所示。规定航班最长延误时间为8 h；机组最长执勤时间为14 h，最长飞行时间为8 h；航班之间最短衔接时间为40 min；航班单位运营延误成本按机型尾流强度分为，重型机4 167 元/h，中型机2 916 元/h，轻型机208 元/h，算例中包含中型机24 架，重型机2 架；旅客单位延误经济损失，国内旅客50 元/h，国际旅客100 元/h；机组空闲成本以50 元/min 计算。

表4 场景算例信息Tab.4 Scenario computational instance information

求解结果如表5所示，场景1 中4 个算例编号分别为1～4，场景2 中4 个算例编号分别为5～8。

表5 求解结果Tab.5 Solution results

随着机场关闭时间和飞机不可用时间变长，恢复成本随之增长，由于时刻表的灵活性，当扰动在一定范围时，可以做出相应调整使航班不被取消，当时间较长时依然会出现航班取消。从模型来看，出现航班取消的时间阈值取决于航空公司所能接受的航班最长延误时间，最长延误时间不同构造出的航班网络不同，如本算例设置为8 h，在航空公司实际应用中可以自行设置模型中的航班最大延误时间，使恢复效果更好。

机场关闭场景的旅客延误分布如图3所示，当机场关闭时间变长时，旅客的延误时间会变长。算例3比算例2 旅客延误分布所在时间段变小，这是由于航班的取消使飞机执行更少的航班，有更大的灵活性保证没有被取消的航班延误程度更小，但是在恢复成本上是不利的。图4显示前4 个算例的成本分布，算例1与算例2 中的客票取消成本显示，一体化恢复模型在不必要取消航班时尽量减少客票取消成本。算例1 ～算例2 的延误损失所占比重大，算例3 ～算例4 中客票取消成本达到近50%，这是由于航班取消导致旅客行程的可行路径减少，取消人数增多。

图4 成本分布Fig.4 Cost distribution

图5～图6对恢复结果中受干扰机场的延误人数与累计延误时间进行统计。算例中设置浦东机场关闭，所采用的航班时刻表中受到影响的航班，其出发机场与目的机场都是武汉或浦东机场，而恢复结果中受影响机场不限于武汉与浦东机场。模型求解中的初始解是顺延方案，不涉及其他机场，一体化恢复模型求解后将两个机场导致的延误分摊到其他机场，降低总成本。

图5 各机场延误人数Fig.5 Delay-passenger number of each airport

图6 各机场累计延误时间Fig.6 Cumulative delay of each airport

飞机故障场景算例旅客延误分布与成本分布如图7～图8所示。飞机故障6 h 与8 h 总成本变化一样，这是因为出现取消航班操作后，被取消航班的后续航班的起飞时间大于故障飞机的最早可用时间。当故障时间变为10 h，总成本会变成301 095 元。客票取消成本与旅客延误损失仍然是主要部分，算例7 与算例8 故障时间较长，但航班取消后，其他航班延误时间比算例6 有所减缓。

图8 成本分布Fig.8 Cost distribution

5 结语

以航班恢复成本为目标函数，摒弃以往分阶段恢复的问题分析方法，综合考虑飞机、机组、旅客建立一体化恢复模型。模型易于理解、算法易实现，扰动场景模拟表明，该模型可在短时间内获得调整方案，并通过机场延误人数、机场累计延误时间、旅客延误分布、恢复成本分布4 个指标说明恢复效果，对航班延误恢复问题具有实际意义。