基于蒙特卡罗算法的管内智能封堵器减振结构优化设计
2020-12-02苗兴园
苗兴园,赵 弘
(中国石油大学(北京) 机械与储运工程学院,北京 102249)
管道运输方式在石油、天然气运输中起着重要的作用。随着使用时间的增长,管道性能逐渐下降,会出现腐蚀、泄漏等现象,对环境造成严重污染,甚至引发重大安全事故[1-3]。近年来,管内智能封堵技术发展较快,许多企业和高校都致力于这方面的研究。张仕民等[4-6]完成了管内智能封堵器的整体结构设计,并对其连接机构、密封特性和锚定性能进行了改进,使封堵器的总体性能更加完善;中油管道检测技术有限责任公司的李振北等人研究了橡胶筒和卡瓦齿形角对封堵和锚定特性的影响[7-8],同时设计出了单节双封型封堵器[9],提高了封堵器的密封特性;赵弘等[10-11]针对封堵器周围流场进行了模拟分析,并在此基础上对封堵器端面的形状和结构进行了优化,同时研究了封堵器不同长度、直径以及长径比对管内流体的影响[12-13],根据模拟结果做出了相应的改进。
在管内智能封堵器工作过程中,周围流场会产生较大的压力脉动,尾部流体区域出现漩涡,造成大量的能量损失,引起封堵器的振动,甚至导致封堵失败。通过对扰流板结构的分析,发现扰流板的角度和面积对管内流场存在较大影响。因此,采用响应面法设计试验方案,建立扰流板角度、面积与封堵前后压力差的数学模型。利用强化学习中的蒙特卡罗算法,用封堵前后的压力差对应封堵器流场环境,将得到的数学模型作为流场环境与扰流板角度、面积之间的映射关系。根据该映射关系,在设定的参数范围内进行迭代搜索,获得压力差最小时对应的扰流板角度和面积,并根据得到的参数建立优化模型,进行数值模拟。
1 管内智能封堵器减振结构模型的建立
1.1 减振结构及工作原理
管内智能封堵器主要包括滑块、挤压碗、承压头、执行器盘、密封圈和推筒等,如图1所示。封堵开始时,封堵器接收到电磁脉冲信号,在管内介质的作用下沿管道向前行进,到达指定位置后由动力系统驱动推筒运动,使滑块沿挤压碗表面滑动,其表面螺纹嵌入管道内壁,使整个机构固定[14-15]。密封圈在受到挤压力时径向膨胀,与管道形成过盈配合,实现管道的密封。针对封堵器的尾部结构进行了改进,在原有结构的基础上设计了3块可折叠控制扰流板,α角为扰流板与底盘的夹角,工作时由动力系统带动弹簧压缩,支撑杆推动扰流板翻转控制α角的大小。
1.2 控制方程的建立
为了方便分析计算,假设管内介质为单相不可压缩流体,且工作过程中温度不变。对于绝大多数流动情况,都需要质量守恒方程和动量守恒方程来进行计算[16-17]。
质量守恒方程:
(1)
式中:ρ为液体介质的密度,kg/m3;ux、uy、uz为微元体在x、y、z方向上的速度分量,m/s。
动量守恒方程:
(2)
(3)
(3)
式中:X、Y、Z为作用在微元体的质量力在x、y、z三个方向上的分量,N;v为运动黏性系数,m2/s。

1—压缩弹簧;2—底盘;3—推筒;4—执行器盘;5—滑块;6—挤压碗;7—密封圈;8—承压头;9—扰流板。
管内流场雷诺数较高,将液体视为不可压缩流体,采用压力-速度耦合方法。为了使流场情况更加贴近实际,选择标准k-ε湍流模型,利用Simple算法进行计算。该湍流方程包括湍流动能k方程和湍流耗散率ε方程:
(5)
(6)
式中:μ为流体动力粘性系数,Pa·s;ε为耗散率;κ为湍动能;μt为湍流粘度系数;其中σk、σε、c1、c2为常数,分别为1.0、1.3、1.44、1.92。
1.3 封堵器周围流场模型
管内智能封堵器周围流场模型如图2所示。
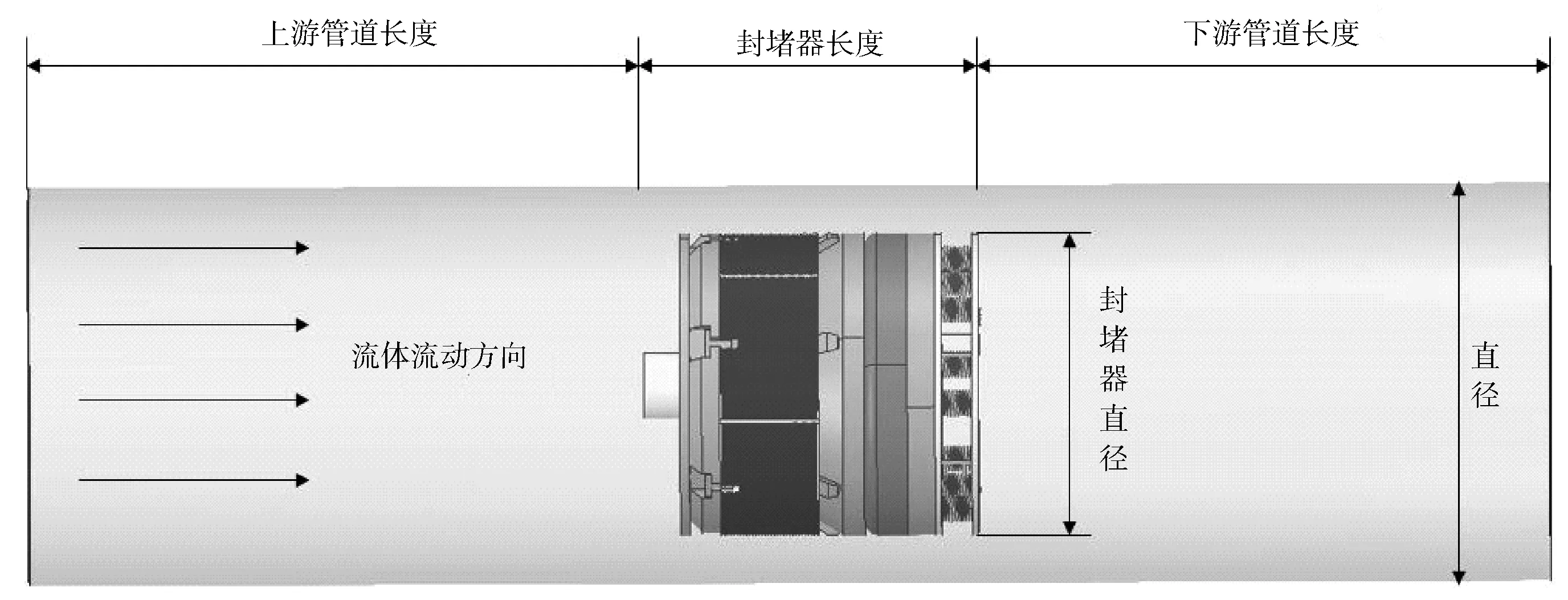
图2 管内智能封堵器周围流场模型
为了方便建模,管道模型选择直管形状,长度为10 m,封堵器中心轴线与管道中心轴线重合,利用ANSYS中的SpaceClaim模块建立三维简化模型,参数如表1所示。数值模拟时管内介质为液态汽油,且为单相流体,其密度为830 kg/m3,黏度系数为0.332 mPa·s。入口边界条件为速度入口,流速为3 m/s,水力直径为0.6 m。出口边界条件为压力出口边界,管壁和封堵器壁面为选择无滑移壁面边界条件。管内操作压力设置为5 MPa,考虑重力影响,方向设为z轴负向。

表1 管内智能封堵器周围流场模型参数 mm
2 封堵器周围流场数值模拟
本次数值模拟选择ANSYS中的Meshing模块进行网格划分,此模块操作简便,精度较高,适用于复杂几何模型。网格形状为四面体结构,将封堵器设置为固体域,管内其它部分设置为流体域,网格类型为CFD网格,设定结点数量后生成体网格,如图3所示。

图3 管内智能封堵器网格模型
为了更加清晰地观察管内流场的分布,选择管道中心截面(z=0的平面)为观测面。当封堵完全时管道将被封死,无法模拟管内流体的流动情况,因此选择封堵状态为99 %时进行研究。封堵过程中会发生压力脉动,在封堵器尾部出现回流和漩涡现象,使封堵器能量损失严重,在封堵时发生振动现象,无法保证封堵的稳定性。为了减少封堵器的能量损失,需要对封堵前后的压力差进行控制,以降低封堵时的压力脉动。由于封堵器尾部流场变化剧烈,因此选择封堵器尾部截面压力的绝对平均值作为观测量。
管道中心截面的压力分布如图4所示,未开始封堵时管道上游压力变化剧烈,呈现明显的梯度分布。封堵器前后端面的压差较大,为封堵器在管道内前进提供了动力。封堵即将结束时管内流场的压力分布比较均匀,封堵器前端面所受压力达到20 MPa,会对封堵器产生一定的冲击,低压区域主要集中在封堵器尾部,这与流场中形成的漩涡有关。封堵即将结束时的压力远远大于未开始封堵时的压力,且低压区范围逐渐增大,压力脉动明显,使得封堵器能量损失严重,封堵时产生振动。

图4 管道中心截面的压力分布
图5为封堵器表面的压力分布图。随着封堵比例的增大,封堵器受力逐渐增大,且表面各部分的压力分界比较明显。封堵器尾部与前端面的压力差距逐渐增大,封堵即将结束时前端面的压力要比尾部压力高1个数量级,这是由于封堵进行过程中密封圈直径增大,到达封堵器尾部的流量逐渐减小。封堵器在封堵前后的受力也存在较大差距,这会导致封堵器状态不稳定,封堵时出现振动现象,影响封堵的稳定性。

图5 封堵器表面的压力分布
管道中心截面的速度分布如图6所示。可以看出,未开始封堵时管内流场的速度变化剧烈,在0~6 m/s波动。由于封堵器的阻隔,使封堵器前端面出现驻点,流体动能损失较大。流体在高压作用下沿封堵器与管壁之间的狭长缝隙高速流过,到达下游后速度降低,且下游区域流体流动情况复杂,封堵器尾部附件有明显的回流和漩涡现象,这会对封堵器造成一定的冲击。封堵即将结束时管内流场速度分布均匀,流速较低,此时管内流体流动较为平稳。

图6 管道中心截面的速度分布
3 基于蒙特卡罗算法的管内智能封堵器减振结构优化设计
通过分析管内流场的分布规律,发现流体的流动情况与扰流板的面积及所处的角度有关,因此可以调整扰流板的角度和面积来使封堵器在管道内部工作状态达到最佳。
3.1 试验设计与结果分析
针对管内智能封堵器扰流板结构的优化问题,选择扰流板的角度和面积为自变量,以封堵前后的压力差为响应量,利用CCD中心试验法设计试验方案。封堵前后的压力差可以反映出封堵过程中的压力脉动,压差越大,说明管内流场的压力脉动就越大,这会导致封堵器尾部的漩涡和回流现象增多,封堵器受到的冲击力变大,在管内工作时的能量损失增加。因此选择封堵前后的压力差来衡量管内流场的稳定性,变量的范围和响应面试验方案分别如表2~3所示。

表2 设计变量
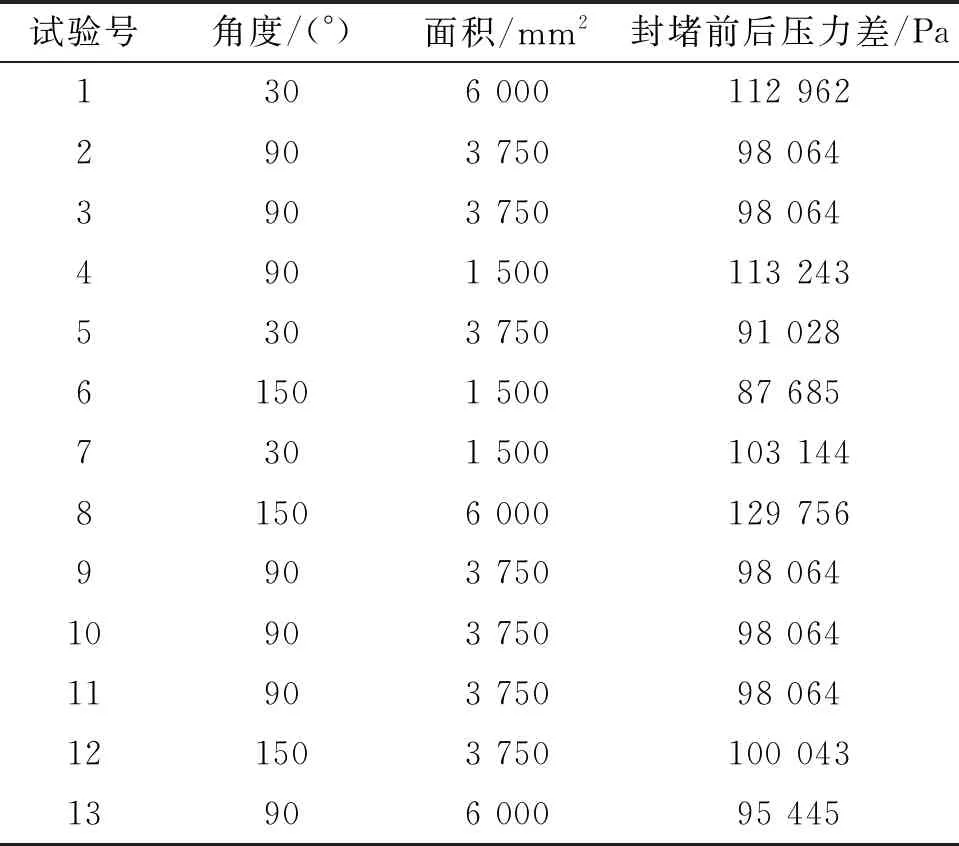
表3 CCD中心试验方案
根据设计的试验方案建立模型,进行数值模拟试验,边界条件与上述相同。在响应面试验中会出现多组中心点,其目的是提高误差估计的准确性[18-19]。由于本次试验没有外界环境影响,因此中心点得出的结果相同。从试验结果可以看出,各组试验物理量的分布情况基本相同,加入扰流板后的压力差相比于原始模型明显降低,说明扰流板可以有效降低封堵时的压力脉动,减少能量损失。但扰流板处于不同角度和面积时,封堵前后的压力差也存在较大差异,这表明扰流板的角度和面积对封堵器的减振效果存在较大影响,通过优化扰流板的参数对于封堵器的减振具有较高的可行性。
封堵前后的压力差与扰流板角度、面积的关系如图7所示。由图7可以看出,关系曲面大致呈抛物面的形状。从角度来看,当扰流板面积较小时,随着角度的增大,压力差逐渐下降;当扰流板面积较大时,随着角度的增大,压力差呈上升趋势。从面积来看,当扰流板角度较小时,随着面积的增大,压力差先减小后增大;当扰流板角度较大时,随着面积的增大,压力差呈上升趋势。因此,扰流板的角度和面积对封堵前后压力差的影响较为显著。
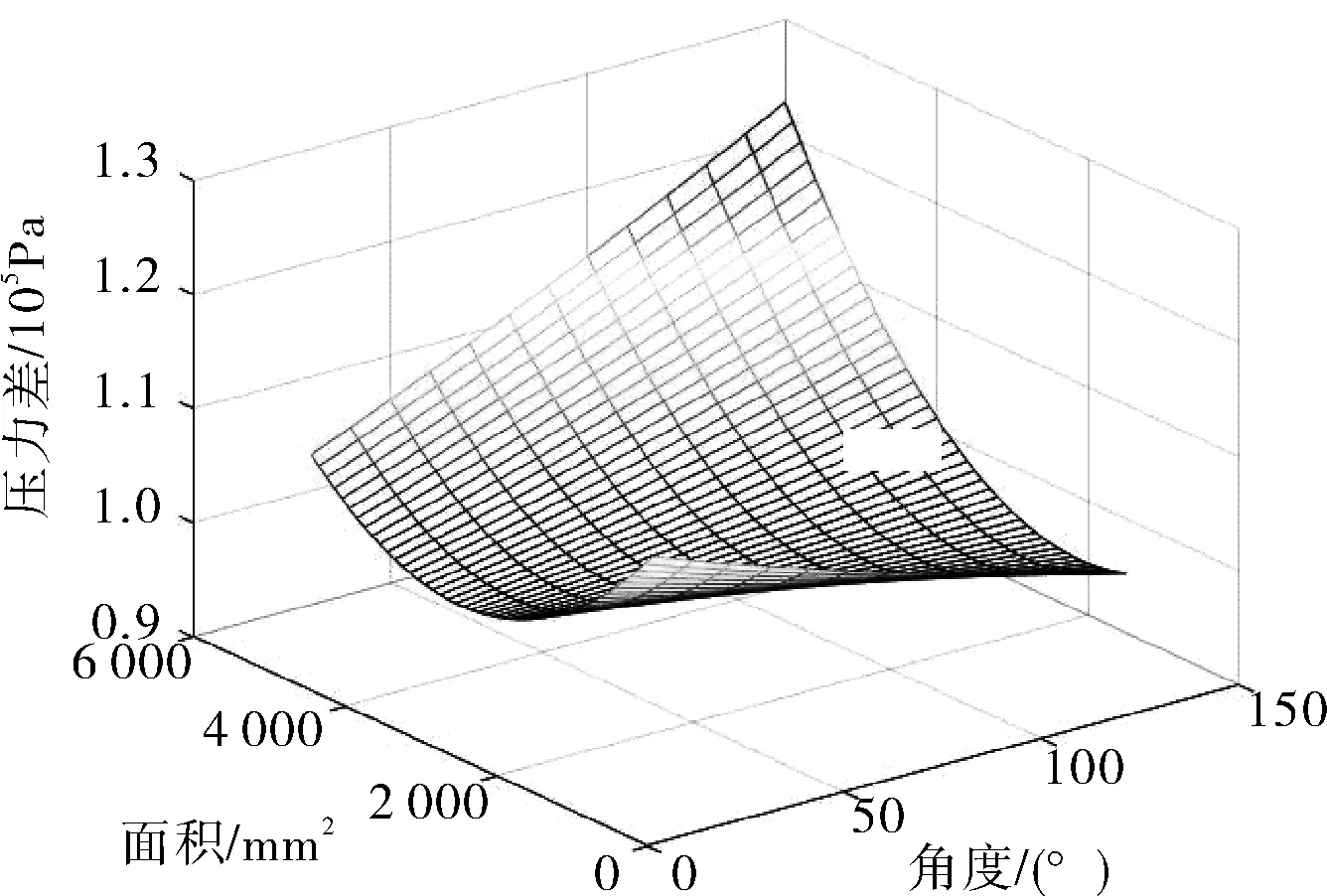
图7 压力差与扰流板角度和面积的关系
利用响应面法对数值模拟试验得出的数据进行拟合,得到Δp与α、S之间的数学模型。
Δp=1.329 63×105-227.424 63×α-
16.853 44×S+0.059 727×α×S+
0.178 89×α2+1.867 11×10-3×S2
(7)
式中:α为扰流板的翻转角度;S为扰流板的面积;Δp为封堵前后封堵器尾部截面的压力差。
通过对数学模型进行方差分析,发现其与试验数据的拟合程度为97.92 %,说明该模型可以较好地预测试验结果,具有较高的可靠性,可以作为目标函数进行封堵器减振结构的优化。
3.2 管内智能封堵器扰流板参数优化
蒙特卡罗算法是一种统计模拟方法,这种方法可以在随机采样的基础上得到近似的结果,并且采样数越多,得到正确结果的概率就越大。它的基本思想是用某个事件出现的频率来估计此事件的概率[20-21],主要步骤为:首先构造概率过程,对于随机问题来说,需要准确描述该过程,对于不是随机性质的问题,则需要构造一个随机的概率过程,将其转化为随机性质的问题;其次就是要实现从概率分布中抽样,已知的概率模型都是由各种概率分布组成的,而随机变量就是蒙特卡罗方法的基本手段。对于均匀分布,随机数就是随机变量,从变量范围内产生随机数就是从均匀分布抽样的问题,随机数是蒙特卡罗方法的基本工具;最后在完成抽样的前提下,需要确定一个变量作为问题求解的对象,通过观察结果,得到问题的解。蒙特卡罗算法适应性强,可以求解模型复杂和计算困难的问题,方法简单,便于编制程序,计算准确性较高,且计算速度快。
管内智能封堵器扰流板参数的优化相当于求解多变量、有约束的非线性最小化问题,其目标函数为:
minΔp=f(α,S)
(8)
约束条件为30°≤α≤150°,1 500 mm2≤S≤6 000 mm2。采用蒙特卡罗算法进行最优化参数求解,其优化流程如图8所示,利用Python语言进行算法程序的设计。将α和S看作指定范围内的均匀分布,生成随机数作为程序的试验点,实现概率分布中的抽样。不断代入随机数求解目标函数值,并将求得的值与上一次的值进行对比,保留最小函数值。为了保证计算的精度,迭代次数设置为108。迭代完成后,得到的最优解参数为α=150 °,S=2 117 mm2。代入到式(7)后,得到此时封堵前后的压力差为Δp=84 529.86 Pa。
4 优化模型与原始模型对比
根据得到的优化参数建立模型,将封堵器扰流板角度设置为150 °,面积为2 117 mm2,设置相同的边界条件进行数值模拟,计算后的响应量明显低于各个试验组,说明优化后的模型可以很好地实现封堵器的减振。按照同样的方法建立管内智能封堵器的原始模型,将优化模型与原始模型进行对比,结果如表4所示。可以看出,优化模型的压力差比原始模型小64.1%,最大压力下降了47.8%,而最大湍动能比原始模型减少了将近1倍。这表明利用蒙特卡罗方法优化的模型可以有效减少封堵过程中的压力脉动,降低管内流体对封堵器的冲击,使流场变得更加稳定,同时减少了漩涡和回流现象,降低封堵器的能量损失,达到减振的目的。
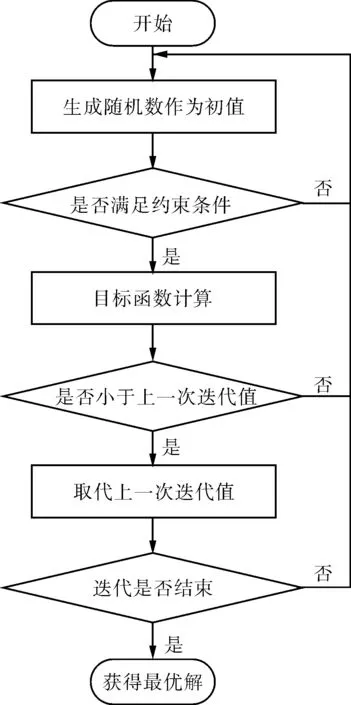
图8 蒙特卡罗算法流程
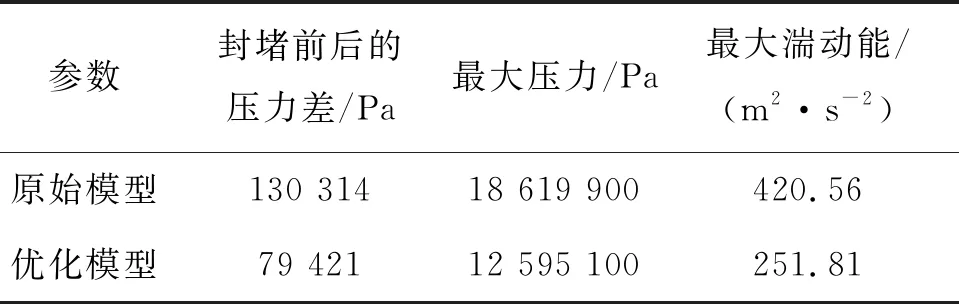
参数封堵前后的压力差/Pa最大压力/Pa最大湍动能/(m2·s-2)原始模型130 31418 619 900420.56优化模型79 42112 595 100251.81
图9~10分别为原始模型与优化模型封堵前后的压力分布图,从图中看出优化模型管内流场的压力比原始模型小,且压力的分布情况大致相同,未封堵时优化模型的压力梯度范围相对较小,因此对封堵器的影响相比于原始模型要小。封堵即将结束时管内流场的压力分布都比较均匀,但从数值上看,优化模型封堵器前端面受力比原始模型小48 %左右,说明蒙特卡罗算法优化后的模型对封堵器产生的压力小,有利于保证封堵的稳定性。
为了更加清晰地对比原始模型与优化模型管内智能封堵器在流场中的受力情况,绘制了不同封堵进度下封堵器尾部所受的压力对比曲线,如图11所示。由图11可以看出,随着封堵的进行,封堵器受力不断增大。从初始状态到封堵70 %过程中,封堵器受力增长的速度比较缓慢,且原始模型与优化模型受力相差不多;封堵70 %以后,封堵器受力的增长速度变快,优化模型与原始模型的差距逐渐增大,表明随着封堵过程的进行,优化模型表现出的作用越来越明显,扰流板对于减少封堵器受力的作用也越来越大,优化后的模型可以减少能量损失,实现封堵器的减振。
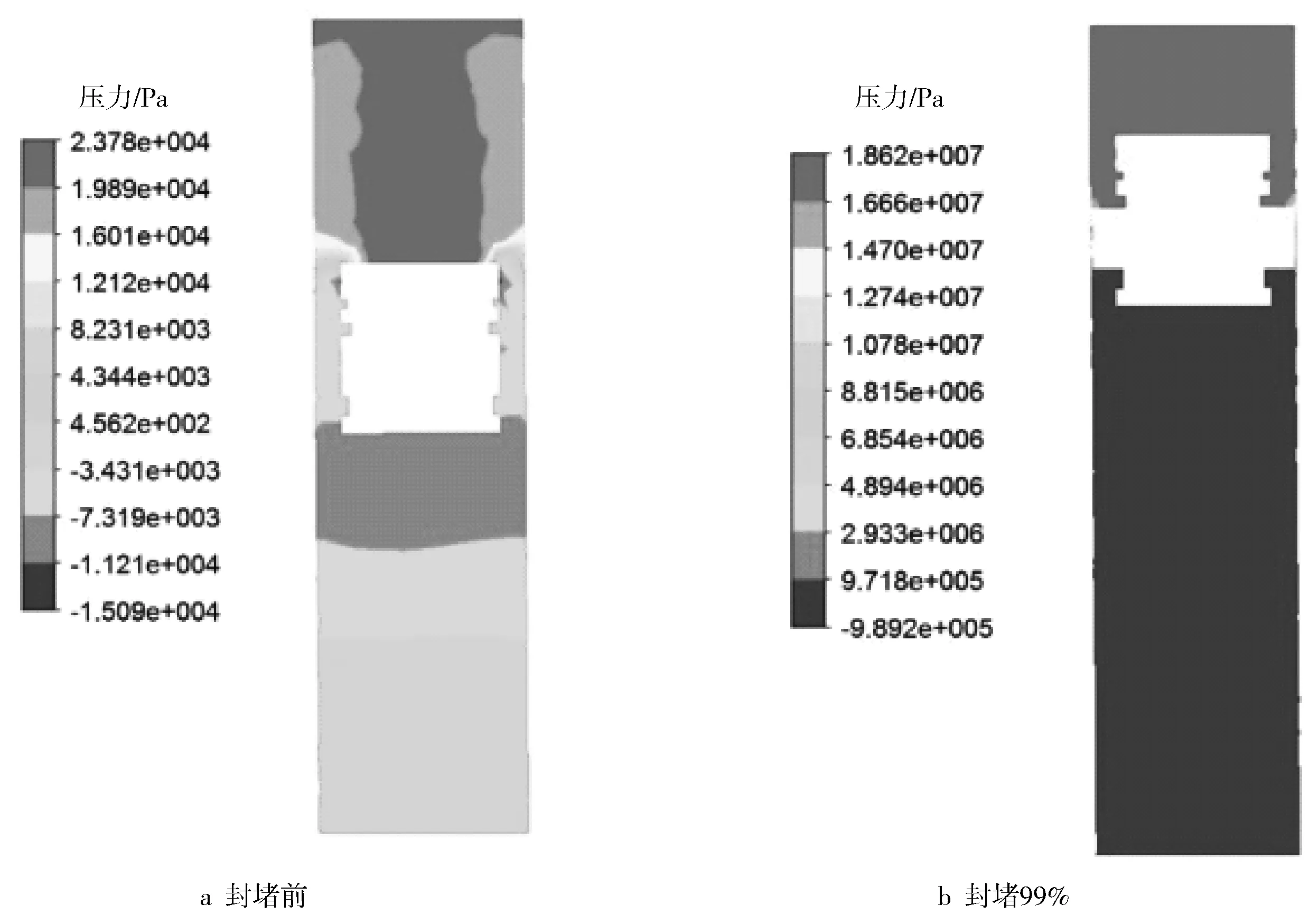
图9 原始模型压力分布云图

图10 优化模型压力分布云图

图11 原始模型与优化模型封堵器受力对比曲线
5 结论
1) 为了解决管内智能封堵器工作过程中的振动问题,在封堵器尾部结构设计3块可折叠扰流板。通过数值模拟发现该结构对管内流场有一定的改善。
2) 利用CCD中心试验方法设计试验方案,建立扰流板角度、面积与封堵前后压力差的数学模型。采用蒙特卡罗算法将压力差作为目标函数,以角度和面积作为参数变量,从中进行抽样、产生随机数。通过不断迭代求解出使目标函数最小的参数,并根据得到的参数建立封堵器模型,进行数值模拟。
3) 优化后的模型相比原始模型封堵前后的压力差明显降低,且最大压力和最大湍动能也显著减少,说明用蒙特卡罗算法优化模型的管内流场的压力脉动降低,封堵器的能量损失减少,有效改善了管内流场,使封堵过程更加稳定,对于减少封堵器的振动具有重要意义。
