受限航路空域自主航迹规划与冲突管理技术

陈雨童，胡明华，杨磊，张昊然，赵征

南京航空航天大学 民航学院，南京 210000

目前，世界范围内空中交通系统正处于全面转型升级阶段，以应对不断增长的飞行需求、复杂庞大的体系结构和多元多变的运行环境。为了缓解日益增长的运输总量与日趋饱和的空域容量间的矛盾，基于航迹运行(TBO)[1]与自由航线空域(FRA)[2]概念应运而生。中国也于2019年发布了基于中国空情的TBO运行概念[3]。TBO的应用得益于星基导航与监视技术的发展以及四维飞行管理系统的完善，这同时也将促进管制员与飞行员情景意识的共享[4]。与当前结构性空域相比，FRA允许用户在空域中按需规划偏好飞行路径，大大提高了航迹运行灵活性，从而促进运行效率和空域容量提升。然而，高密度FRA中的航迹运行，管制员工作负荷成为制约空域容量和整体运行性能进一步提升的关键因素[5]。尤其在空域受限、容量降级情况下，航空器轨迹的强关联性往往引发冲突多米诺效应，导致管制员认知难度和工作负荷的爆发式增长，从而大幅增加运行风险[6]。因此，迫切需要建立一种新型的自主航迹冲突探测与解脱技术，以实现自由航线空域四维航迹运行[7]。

自主空中交通管理技术最早由美国提出，即自由飞行(Free Flight)[8-9]，旨在有效降低额外的燃油消耗的飞行时间，并减少空域拥堵。而针对TBO的战术级自主四维航迹运行技术的研究仅刚起步。尽管大部分自由飞行的研究并不面向TBO，但相关成果依然能够为基于航迹的自主空中交通管理技术的研究提供重要参考和有力支撑。在自由飞行的研究中，根据控制模型，主要分为两类：集中式控制和分布式控制。

集中式控制的优点在于能够基于全局信息求解全局最优解，随之而来的缺点是计算成本较高，难以满足实时运行需求。因此，集中式控制模式下的自由飞行技术往往用于预战术阶段。起初，主要通过线性规划方法建立冲突解脱模型，并运用最优化控制理论进行求解[10]。在此基础上，优先权概念的引入使涉及多机冲突群的航空器能够根据优先次序先后进行解脱，同时，微分对策理论被用来解决因不确定性所引发的冲突[11]。随后，遗传算法[12]、免疫遗传算法[13]等人工智能算法逐步被应用到自由飞行冲突解脱中，并且多种智能算法组成的集成算法的解脱效果被证明优于单一算法[14]。多个实验证明，对冲突航迹的多次规划[15]或分步骤解脱[16]效果要好于一次性的解脱。另外，对空间进行离散化处理使冲突模型的复杂性大幅降低，从而能够有效提升计算速度[17]。除了常态下的自由飞行研究外，基于受限空域的研究也逐步进入了研究者的视野[18]。

与集中式控制相反，分布式控制的优点是计算成本较低，但缺点是无法保证求得全局最优解。因此，分布式控制往往用于战术阶段(在空中交通管理中的分布式控制通常是指将部分管制职能转移到机载端)。混杂动力学的发展与成熟推动了分布式控制在空中交通管理中的发展[19]，且分布式人工智能被广泛运用于其中[20-22]。实验表明，分布式控制在高密度条件下的空域中具有更强的鲁棒性和更少的冲突[23]。由于分布式控制具有更高的不确定性，不确定性这一因素在分布式控制的研究中被更多地考虑[24]。空间的离散化方法在分布式控制中同样得到了很好的运用[25]，并且引入了元胞自动机的方法[26]，为求解带来了便利。

在TBO方面，研究者们对基于TBO的运行环境[27]、管理系统[28]、复杂性分析[29]、冲突概率[30]、容流管理[31]等方面开展了一些研究。而国内的TBO研究主要面向的是终端区的运行[32-33]，并多聚焦于航迹预测[34-36]。总体来看，面向自由飞行的TBO研究鲜见报道。

纵观近20年来有关自由飞行的学术研究，虽然其为空管自动化发展提供了一个潜力巨大的方向，但是空管系统尤其是管制活动仍然处于所谓的“以人为本”的模式，即将人放在控制系统的核心位置。即使在低密度空域中，也没有能够真正地实现自由飞行。因此，为了推动空管自主运行的进展，在系统设计中应当充分考虑人机协作的关键问题[37]：① 人在任何情况下都能够安全地接管操作；② 机器的机制必须是透明且易于人理解的；③ 人机意识应当高度同步；④ 自动化程度允许动态调整；⑤ 最重要的是人和技术都要适应这一管理理念。有鉴于此，在本文中，我们借助几何模型提出了应用于受限FRA中的两阶段实时自主四维航迹冲突探测和解脱技术，以增加管制员、飞行员和自动化系统之间的决策透明度，为TBO下的自主空中交通管理变革提供新思路和新方法。

为了实现这一愿景，本文开展了如下工作：

1) 引入了基于栅格的空域离散化概念，以提高计算效率。

2) 提出了一种使用可视图(Visibility-Graphic)理论和Dijkstra算法来避免多个限制区域的期望轨迹(Desired Trajectory)[38]的自主规划方法。

3) 通过解析几何辅助实现改航可达时空域可视化，建立了“后到先调整”(Later-Entry-First-Adjust, LEFA)原则下的实时自主四维航迹冲突探测和解脱模型，以增强战术运行态势的空地协同感知。

4) 以中国西部的某航路扇区为例，通过快速仿真验证了该方法的可行性和有效性,并对栅格尺寸和探测距离这2个关键参数进行了灵敏度分析。

1 基于栅格的空域离散化

FRA是一种由欧控(EUROCONTROL)提出的新型空域，正被逐步应用于实践之中，旨在提高空中交通运行效率和成本效益等。在FRA运行中，用户可以自行规划其在扇区的进入点和出口点之间的航线，无需受到固定空中交通服务航线网络的限制。需要说明的是，考虑到采用上升或下降高度进行冲突解脱，其经济性较差，且空地四维认知复杂度较高，自主运行模式下潜在风险较大，因此，本文以FRA单高度层为研究对象开展自主航迹运行问题的初步探索。

在TBO背景下，航空器需要在关键航路点满足受控到达时间(CTA)要求，即当航空器遭遇冲突时，自动化系统需要搜索合适的改航航路点和相应的速度，以使航空器在扇区的进入点和出口点尽可能满足CTA要求。由于在连续空间中搜索精确最优改航航路点非常耗时，因此，本文将空域划分成一系列整齐排列的正方形栅格对空域进行离散化。考虑到实时决策的时间限制，必须在寻优精度和计算速度之间进行权衡。这种权衡将由一系列关键运行参数决定，如栅格大小、导航精度、航空器性能、扇区尺寸等。另外，基于栅格的空域离散化另一个优点是栅格可以直观地区分空域中不同区域的状态，如图1所示。

基于经(X轴)纬(Y轴)度，空域被划分为若干栅格。每个栅格都有其对应的栅格坐标(为了便于区分，本文将用以指示栅格排列位置的坐标称作“栅格坐标”，用以指示位置点实际位置坐标称作“实际坐标”)，如C(X,Y)表示栅格坐标为(X,Y)的栅格。定义3种基本类型栅格，分别是：限制栅格、保护栅格、可用栅格。其中，限制栅格指受限空域(因恶劣天气、军事活动等影响导致不可飞行)所占用的栅格，需要特别说明的是，基于安全考虑，该栅格内只要存在限制空域，无论是否被完全占据，均认定为限制栅格，如图1中C(2,4)和C(3,4)；保护栅格是指与限制栅格邻接的一层或数层栅格，如图1中C(1,4)，当栅格尺寸大于等于航空器与限制区的安全间隔，则仅设置一层保护栅格，反之，设置多层保护栅格，层数为该安全间隔除以栅格尺寸的商向上取整，即确保保护栅格的厚度不小于该安全间隔，显然栅格尺寸越小，形成的限制栅格与保护栅格越精确；可用栅格指空域内可用于航空器飞行的栅格，即空域内除限制栅格和保护栅格以外的栅格，如图1中C(0,4)。此外，将限制栅格和保护栅格统称为不可用栅格。

图1 基于栅格的空域离散化Fig.1 Grid-based airspace discretization

对于任意栅格，均具有5个主要位置点，即中心点、左上点、右上点、左下点、右下点，如图2所示。假设栅格边长为S，坐标系原点的实际坐标为(x0,y0)，那么C(X,Y)的5个主要位置点的实际坐标可以表示为

(1)

式中：PC、PTL、PTR、PBL和PBR分别表示中心点、左上点、右上点、左下点和右下点的实际坐标。

总的来说，基于栅格的空域离散化主要为实现以下3个功能：① 通过栅格分类使航空器仅能在可用栅格中飞行，从而确保航空器不会因为意外闯入限制区而造成危险；② 在航空器规划期望航迹时，不可用栅格凸边界的顶点的可用栅格的中心点将被用作改航路径的备选航路点；③ 航空器自主冲突避让的改航航路点亦为栅格中心点。可见，以栅格中心点为航迹状态变更点是下文自主航迹规划与冲突解脱策略生成的核心规则之一。

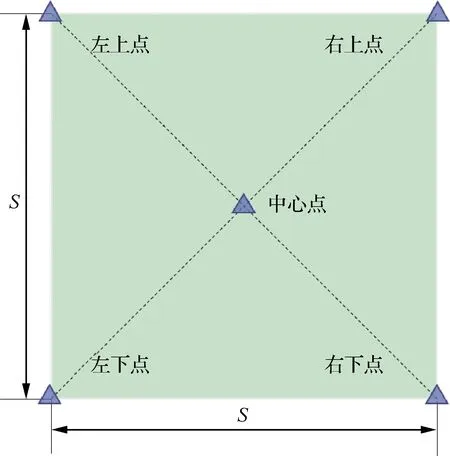
图2 栅格主要位置点Fig.2 Main positional points of grid

2 阶段1：多限制区约束下的期望航迹自主规划

TBO的愿景是通过持续滚动的航迹协商，在起飞前生成满足机场及空域容量限制的无冲突四维轨迹。然而，在实际运行过程中，受临时性和动态性的恶劣天气和军事活动影响，飞行过程航迹实时协商调整不可避免。因此，在航空器进入受限扇区之前，将既有商定航迹[38]更新为满足限制区约束的期望航迹(称这一过程为“调整过程”)是至关重要的。应当指出的是，为所有即将进入空域的航空器集中规划满足各自偏好的全局优化无冲突航迹(Conflict-free Trajectory)[39]是耗时且低效的。因此，提出了一种2阶段自主航迹运行方法，即基于网络的期望航迹重规划方法(阶段1：调整阶段)和基于时空棱锥的实时自主四维航迹冲突探测解脱方法(阶段2：实时阶段)。

阶段1的自主期望航迹规划需要依托“空-地”共享空域数据，特别是限制区位置和几何构型。根据空域信息、飞行器性能和飞行员的个人偏好，在限制区约束下有效规划最短飞行路径及相应的飞行速度。为了便于展开，本文假设飞行员具有一致性偏好，即以经济速度沿最短路径飞行。

基于此，将“可视图法”[40]引入路径规划，以期有效且直观地搜索限制区约束下的最短飞行路径。可视图构造方法如下：将待搜索路径的起点、终点以及不可用栅格凸边界的顶点的可用栅格的中心点作为点，这些点两两相连所连成的未穿过不可用栅格的线段作为边，以此形成的无向图即为可视图[41],如图3所示。

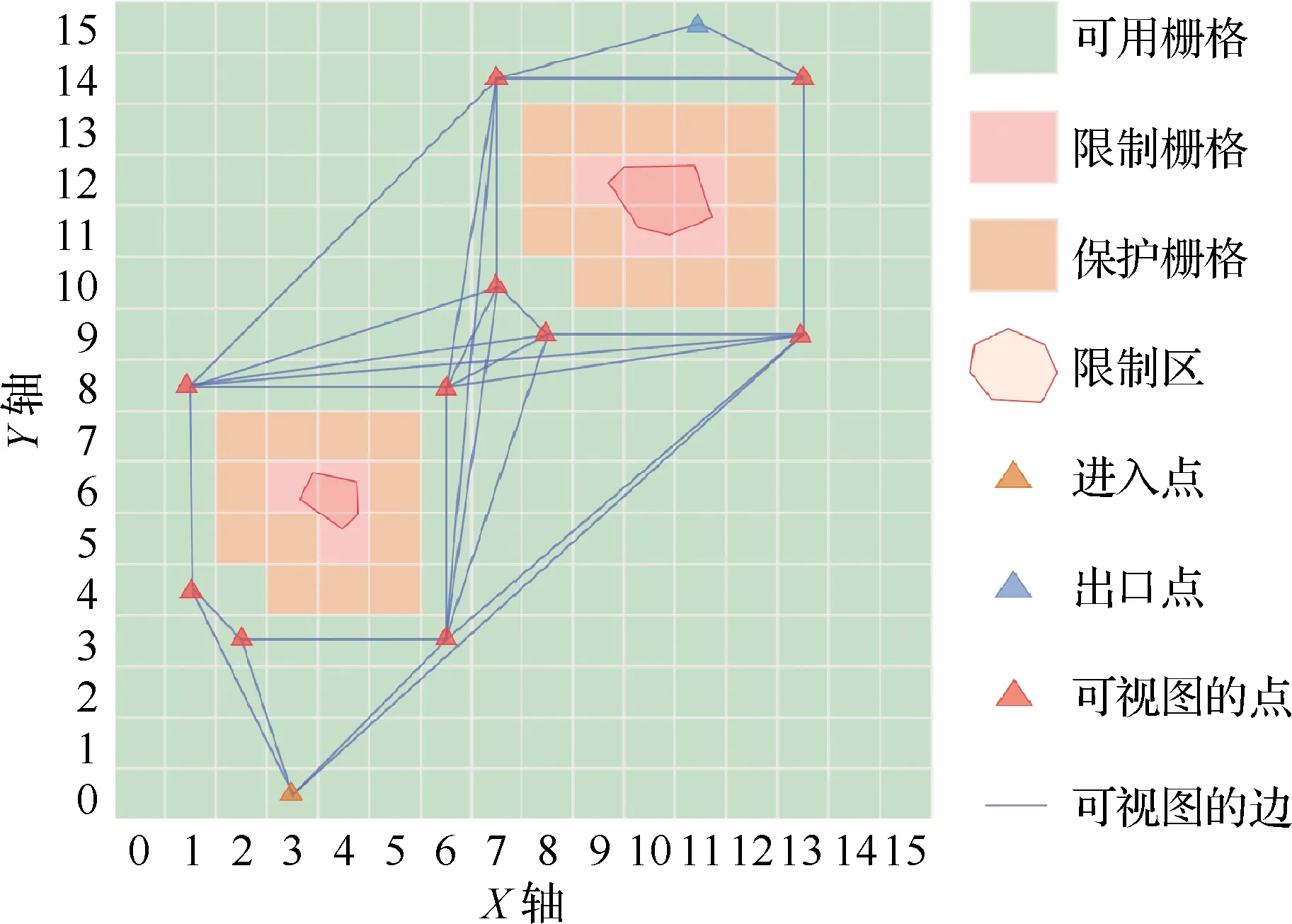
图3 可视图Fig.3 Visibility graphs

G(V,E,φ)表示基于限制区约束的可视图结构，其中，V表示图中所有点的集合，E表示图中所有边的集合，φ为点和边的对应法则。基于可视图理论和空域离散化的特点，令

V1=

(2)

V2={v|Pv=PI或PO}

(3)

V=V1∪V2

(4)

E={e|φ(e)=vi,vj,vi,vj∈V}

(5)

φ(e)=vi,vj,∀C(X,Y)∩|vivj|=∅,

C(X,Y)∈Rl,l∈L

(6)

式中：v为图中的点；Pv为点v的实际坐标；Rl为限制区l形成的不可用栅格的集合;L为所有限制区l的集合;PI和PO分别为该航空器在该空域中的进入点和出口点的实际坐标；e为图中的边；|vivj|为点vi和点vj的连线。

可视图的边为无向边，边的权值为连接该边两点间的实际距离。基于可视图，运用Dijkstra算法[42]在所生成无向加权图中搜索出最短路径，并基于经济速度假设，航空器即可在空域受限信息共享支撑下，快速重新规划在空域内的期望航迹，从而在进入空域后更加专注于与其他航空器之间的冲突探测与解脱，从而提高实时运行效率。

3 阶段2：基于时空棱锥的实时自主四维航迹冲突探测解脱

航空器在进入目标空域后将沿期望航迹飞行，依据空地共享的空域交通态势和航空器飞行意图信息，持续探测潜在航迹冲突，适时规划无冲突航迹。因此，阶段2中航空器自主航迹管理行为包括空间位置推测、潜在冲突探测和实时冲突调解。

3.1 空间位置推测

为了实现高效的冲突探测和解脱，将时间进行离散化处理且航空器位置推测的取样间隔为T，即每T个单位时间更新一次航空器位置信息，如图4所示。

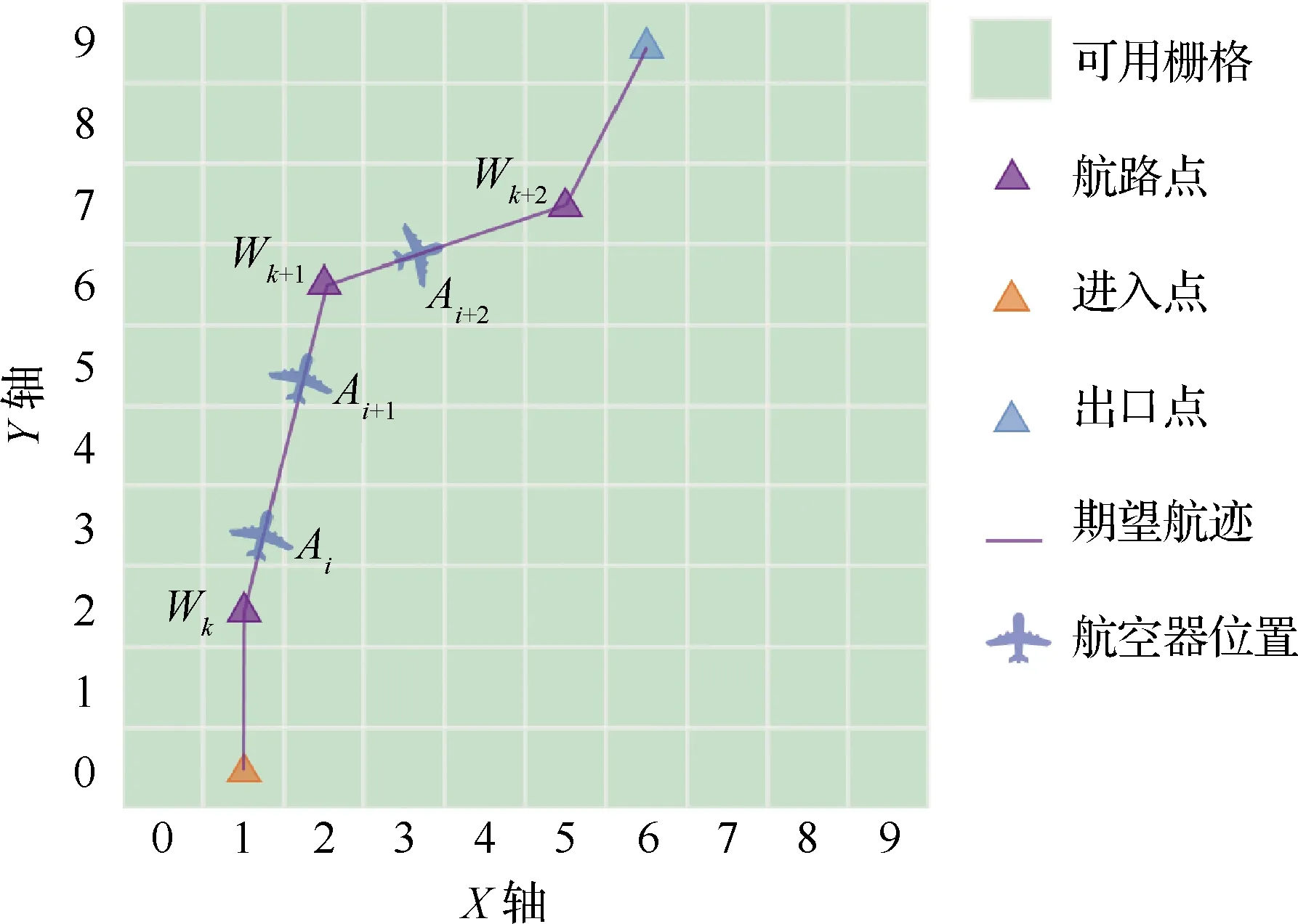
图4 航空器实时位置更新Fig.4 Aircraft real-time position update

例如，某航空器沿其期望航迹飞行，途径3个航路点，分别为Wk、Wk+1、Wk+2,与之对应的实际坐标分别为(xk,yk)、(xk+1,yk+1)、(xk+2,yk+2)，CTA分别为Tk、Tk+1、Tk+2。图中的3个航空器位置点Ai、Ai+1、Ai+2分别表示该航空器在ti、ti+1、ti+2时刻的实时位置。其中，ti表示航空器进行第i次冲突探测的时刻。因为每次更新的时间间隔为T，所以有

ti+1=ti+T

(7)

假设该航空器在ti、ti+1、ti+2这3个时刻的位置的实际坐标分别是(xi,yi)、(xi+1,yi+1)、(xi+2,yi+2)。在此模型下，假设航空器的运动状态为匀速直线运动，根据航空器位置更新后是否仍然处于当前航段，共有2种情况。

情况1位置更新后航空器仍然处于当前航段，如图4中从ti推测至ti+1。此时，

(8)

式中：P(t)为t时刻该航空器位置的实际坐标，且x(t)和y(t)分别对应其横坐标和纵坐标。

情况2位置更新后航空器已处于下一航段，如图4中从ti+1推测至ti+2。此时，

P(t)=(x(t),y(t))=

(9)

3.2 潜在冲突探测

基于航空器周期性位置推测，考虑空域内航迹意图执行的不确定性，为提升冲突探测的鲁棒性，提出一种局部冲突探测方法,如图5所示。定义RC表示航空器主动性冲突探测半径,航空器仅探测该距离范围内的潜在冲突。

图5中，探测航空器是指主动执行冲突探测的航空器；在探测范围内的航空器被称为被探测航空器；在外部的航空器则被称为未被探测航空器。这里仅考虑探测航空器与被探测航空器之间的潜在冲突。采用局部探测的优势在于它可以有效节省计算资源以提高计算速度，这对于自主航迹运行中的安全性和效率至关重要。并且，在实际运行中，航迹位置的不确定性随着时间提前量的增加而增加，探测一定范围内的潜在冲突可以有效降低虚警率和漏警率[43]。因此，无论是仿真还是现实运行，探测半径设置的合理性将显著影响航迹效率。

本文主要以巡航阶段运行为例，因此定义航空器之间最小水平安全间隔为SS。显然，当且仅当在飞行过程中的某个时刻任何2架航空器之间的最小水平间隔小于SS时，即可判定航空器间存在潜在飞行冲突。如3.1节中所述，航空器位置每次更新都有2种情况，那么2架航空器每次位置更新后的相对位置表达式就有4种情况,如图6 所示。

图5 局部冲突探测Fig.5 Local conflict detection

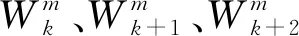
(10)

可见，航空器在每一个航段均为匀速直线运动，所以航空器的位置是随时间线性变化的。航空器之间距离的平方是关于t的分段函数，每个分段都是二次函数。第i段可以表示为

(11)

(12)

经上述推导易得，在当前航段飞行过程中，2架航空器之间的最小距离为

mins(t)=min{minsi(t)}

(13)

3.3 实时冲突调解

3.3.1 基于时空棱锥的航迹可达时空域图形建模

在冲突解脱中，为了强化航空器自主运行中管制员、飞行员和辅助决策系统之间的认知同步，引入了时间地理学中的时空棱锥(STP)理论[44]。通过基于CTA的STP模型，可以推导出航空器的潜在改航路径存在于一个特定的椭圆形可达时空域范围内(如图7所示)。

(x,y)=PC(X,Y)

(14)

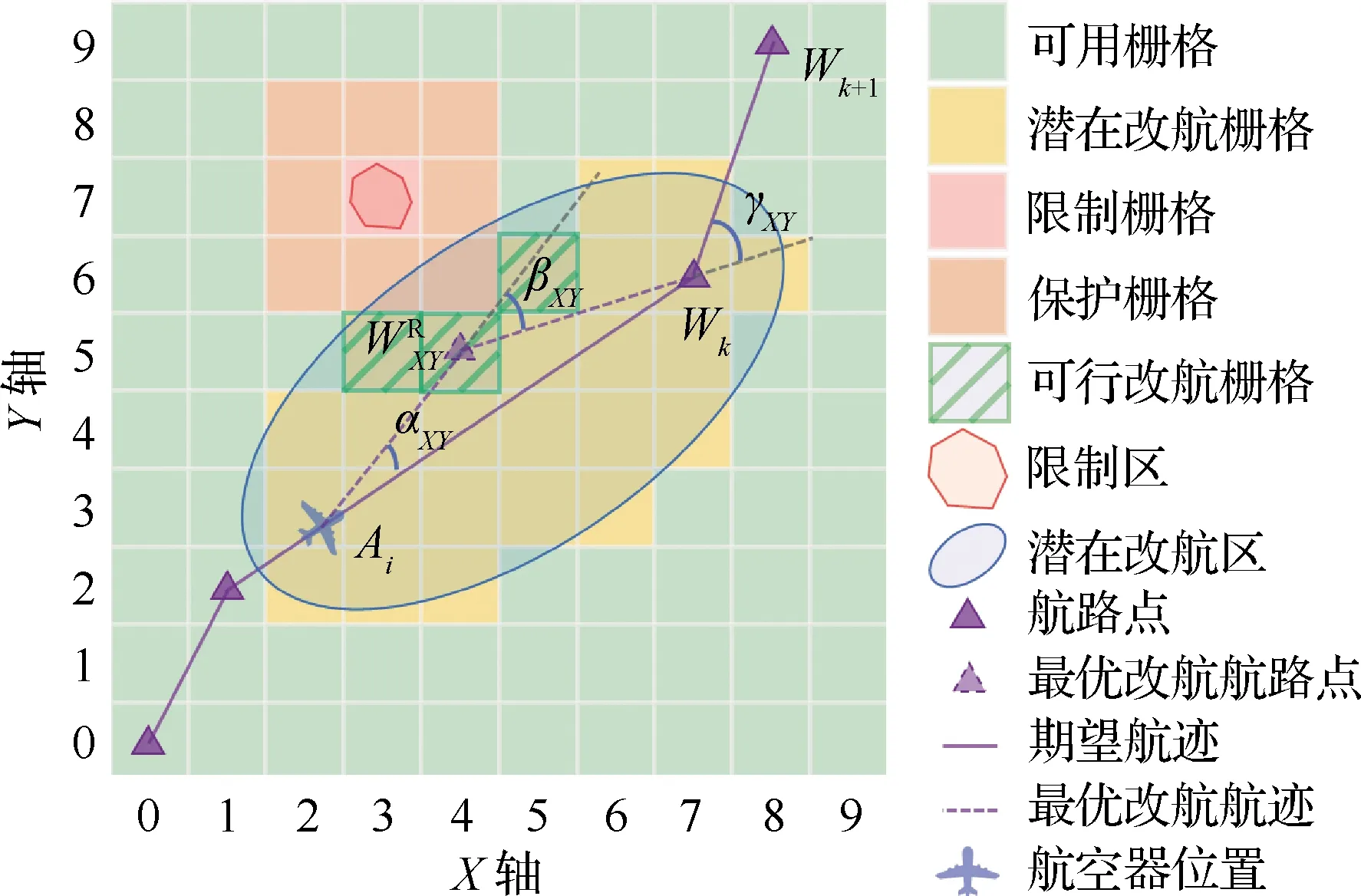
图7 基于时空棱锥的改航Fig.7 Digram of STP-based rerouting optimization

考虑到CTA约束，可以得到以下约束：

(15)

其中：

Δt=Tk-ti

(16)

即

(17)

式中：vmax为航空器的最大航速。

由式(15)可知，所有可行的改航航路点(x,y)均处于一个椭圆之中，即

(18)

其中：

(19)

由此，可为每个航空器生成可达时空域图形，如图7所示，并与空域态势相融合，为驾驶舱和管制员提供一致的、友好的航迹冲突显示，亦能提升自动化无冲突航迹规划策略的透明度和可理解度。

3.3.2 最短无冲突航迹规划

依据航迹可达时空域，椭圆内除不可用栅格外的栅格集合即为该航空器无冲突改航航迹的搜索空间。为了简化问题，遵循“后到先调整”原则，即当航空器之间存在潜在冲突时，后进入该空域的航空器优先进行航迹调整。该LEFA原则与“先到先服务”原则(First-Come-First-Served, FCFS)等价，都遵循着先到者具有更高优先级的原则。

1) 目标函数

本文航迹优化将CTA纳入考量范围，即在规划冲突解脱航迹时，应尽可能通过调速满足受制到达时间限制。由于航迹可达域内的改航航路点均能满足CTA要求，故本文的优化目标为改航航迹最短，记为

minZ=f(X,Y)

(20)

式中：f(X,Y)为当航空器以PC(X,Y)为改航航路点时改航航段的飞行距离。

2) 约束条件

(1) 限制区约束。改航航路点应为可用栅格的中心点，即改航航路点不应处于不可用栅格内：

C(X,Y)∉Rl,l∈L

(21)

同时，改航航迹不能穿越限制区，即

(22)

(2) 转弯角约束。考虑到航空器性能限制，潜在改航航路点需要满足航空器转弯角度的限制。假设最大转弯角度为TA，则有

αXY,βXY,γXY≤TA

(23)

式中：αXY、βXY、γXY分别为出航角、归航角和航迹恢复角，如图7所示。

(3) 最小安全间隔约束。基于局部冲突探测中提到的冲突探测方法，改航航迹应满足最小安全间隔：

mins(X,Y),d≥SS,d∈D

(24)

式中：mins(X,Y)为当该航空器以PC(X,Y)为改航航路点时，其与被探测航空器d的最短距离;D为被探测航空器的集合。

综上，最短无冲突航迹规划模型为

minZ=f(X,Y)

(25)

特别地，当所有潜在改航栅格均不能完全满足约束(即以当前CTA要求无可行解)时，航空器采用适应性过减速机制(即允许延误，适当推迟后续航路点CTA)。由式(16)、式(18)、式(19)可知，推迟CTA将使Δt变大，进而使椭圆的参数a和b增大，从而增大潜在改航区的范围，增大解空间，如图8所示。

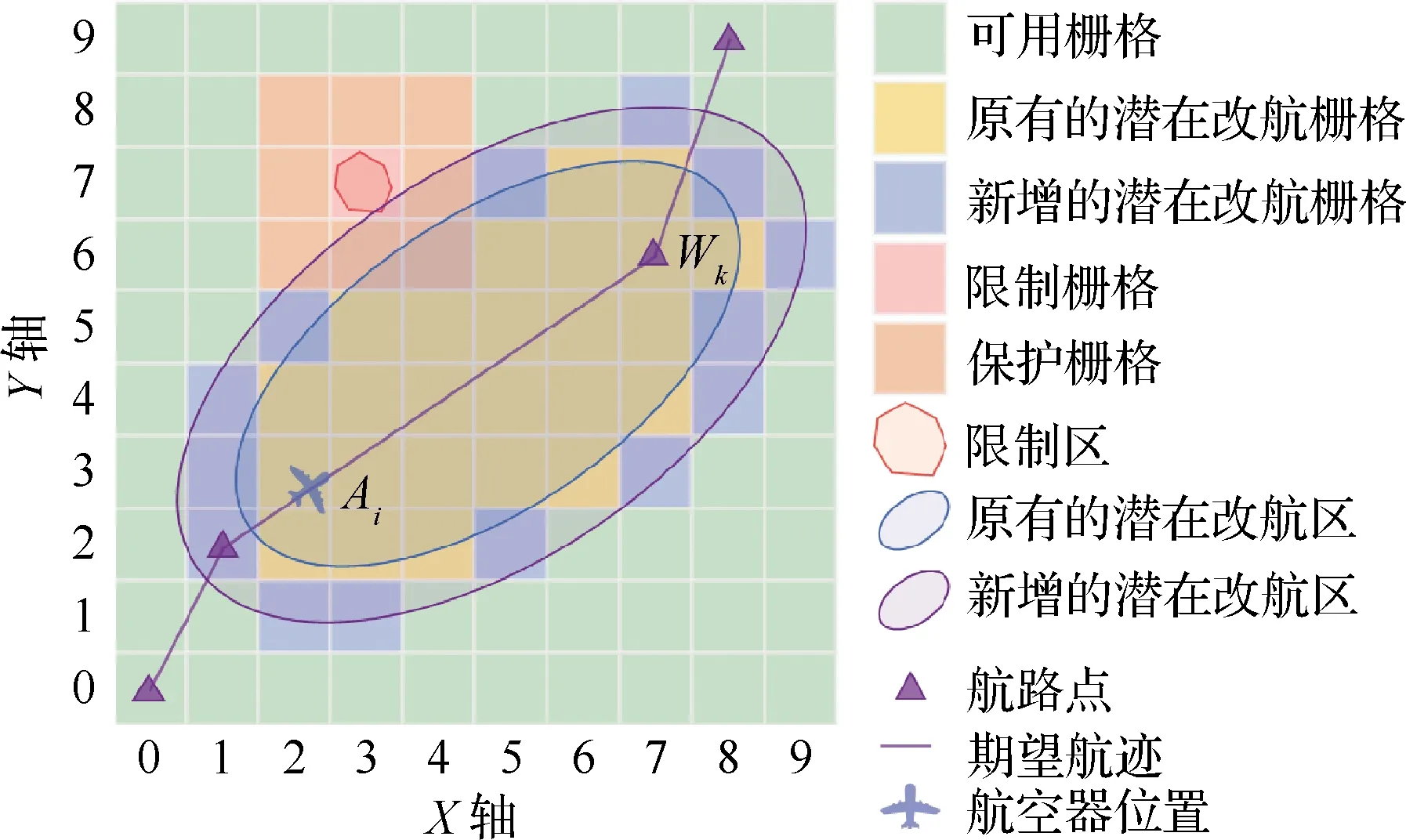
图8 拓展潜在改航区范围Fig.8 Expansion of potential rerouting space

3) 求解算法

由上述优化模型可知，该模型为非线性整数规划模型，然而由于该模型仅有2个决策变量，即X和Y，且在栅格尺寸不是非常小时待搜索的潜在改航栅格数量非常有限，故采用枚举法，遍历所有潜在改航栅格，通过上述约束条件筛选出可行改航栅格，从中选取最优改航栅格，即可得到最优改航航路点及相应的改航航迹。需要进一步说明的是，采用枚举法旨在增加自主系统的透明性，使其在实际运行中更好地适应人机交互需求，即在人机交互界面中不仅显示可达域中每个潜在改航航路点是否可行，亦能够显示每一个可行改航航路点的收益(如飞行距离、飞行时间、燃油消耗等)，这样不但更好地实现了人机意识同步，也能够在某些情况下管制员或飞行员需要人工选择非最优改航航路点时，为其提供更多的辅助决策信息。

冲突探测和解脱的总体流程图如图9所示。可以预期，基于航迹时空可达域的无冲突航迹实时规划不仅能够支撑自由航线空域内自主航迹运行，亦提供了一致的情景意识和透明友好的人机接口，尤其是发生特情时，管制员或飞行员可以安全无缝地接管空域或航空器运行，有效降低自主运行潜在风险。

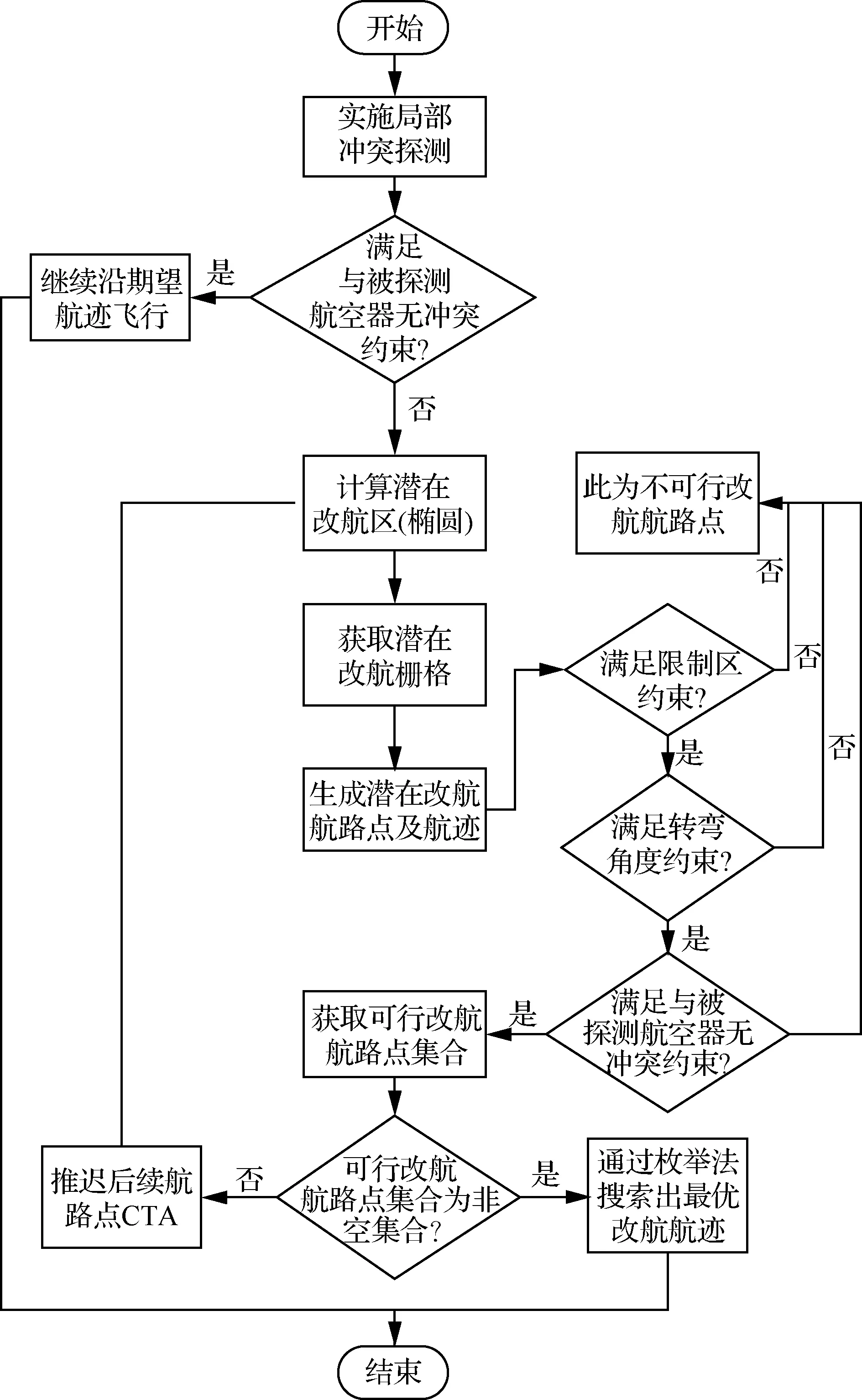
图9 冲突探测和解脱流程图Fig.9 Conflict detection and resolution flow chart

4 仿真算例

4.1 场景构建

本算例选取中国西部典型高空航路扇区兰州7扇(ZLLL07)为仿真场景。为了验证本文提出的自主航迹规划技术，研究了飞行密度最高的飞行高度层(FL310)的运行情况。首先使用米勒(Miller)圆柱投影法[45]将扇区边界的顶点的经纬度坐标转换为平面坐标，如图10所示。

基于TBO的运行概念，随机生成了100条波音737机型航空器的无冲突商定航迹，飞行器进入空域的时间间隔是60 s。随后生成了数个限制区(1个军事活动区和2个危险天气区)，限制区与62%的商定航迹存在冲突，故需要在航空器进入前生成各自期望航迹。考虑现实运行规则，将航空器最小水平安全间隔设置为10 km，同时将栅格边长也设置为与其相同的数值。需要说明的是，从长期运行看，应考虑危险天气的动态变化情况，如通过增加安全间隔裕度，或将其作为缓慢移动物体进行处理，能够直接融入本文所提出的模型中。然而，考虑到危险天气区域(如雷暴)移动速度一般小于1 km/min，其移动对已进入空域的单架航空器的影响相对较小。因此，为简化问题，本文对限制区作出静态假设。

基于BADA数据库波音737机型的性能参数，无风环境下航空器经济航速与最大航速分别设置为828 km/h和876 km/h；航空器允许实施的最大转弯角度设置为90°。航空器在进入该空域后，每10 s执行一次自主冲突探测和解脱，探测距离为50 km，即探测范围为以探测航空器为圆心，50 km为半径的圆区域。

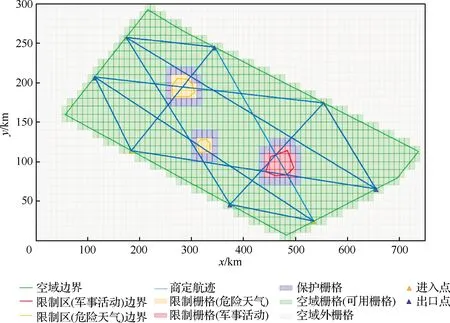
图10 无冲突商定航迹Fig.10 Agreed conflict-free trajectories

4.2 仿真结果

基于仿真场景及其基本参数，生成了所有航空器以经济航速飞行、且满足限制区约束的期望航迹，如图11所示。整个空域内自主运行过程中，共探测到35次潜在冲突，涉及潜在冲突的航空器共46架，其中43.5%发生了超过1次的潜在冲突。最终的无冲突执行航迹[38]如图12(平面维度)和图13(时空维度)所示。考虑到TBO下的冲突探测和解脱规则，在运行阶段，当因改航产生额外飞行距离时，航空器将通过加速来尽可能满足CTA要求。然而，如果航空器以最大飞行速度运行尚且不能满足CTA要求，那么航空器自主计算生成一个新的CTA，即延误产生。

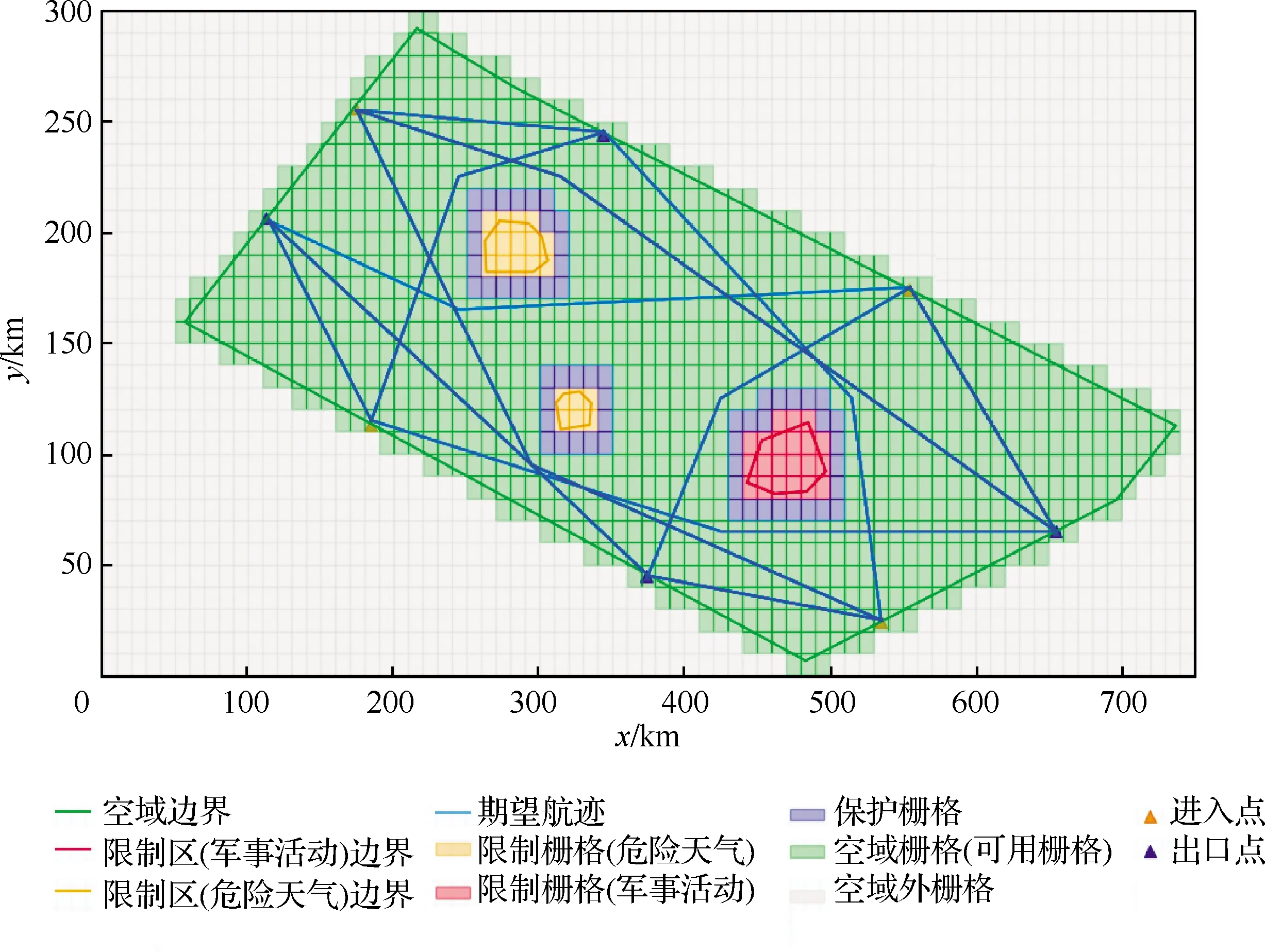
图11 期望航迹Fig.11 Desired trajectories

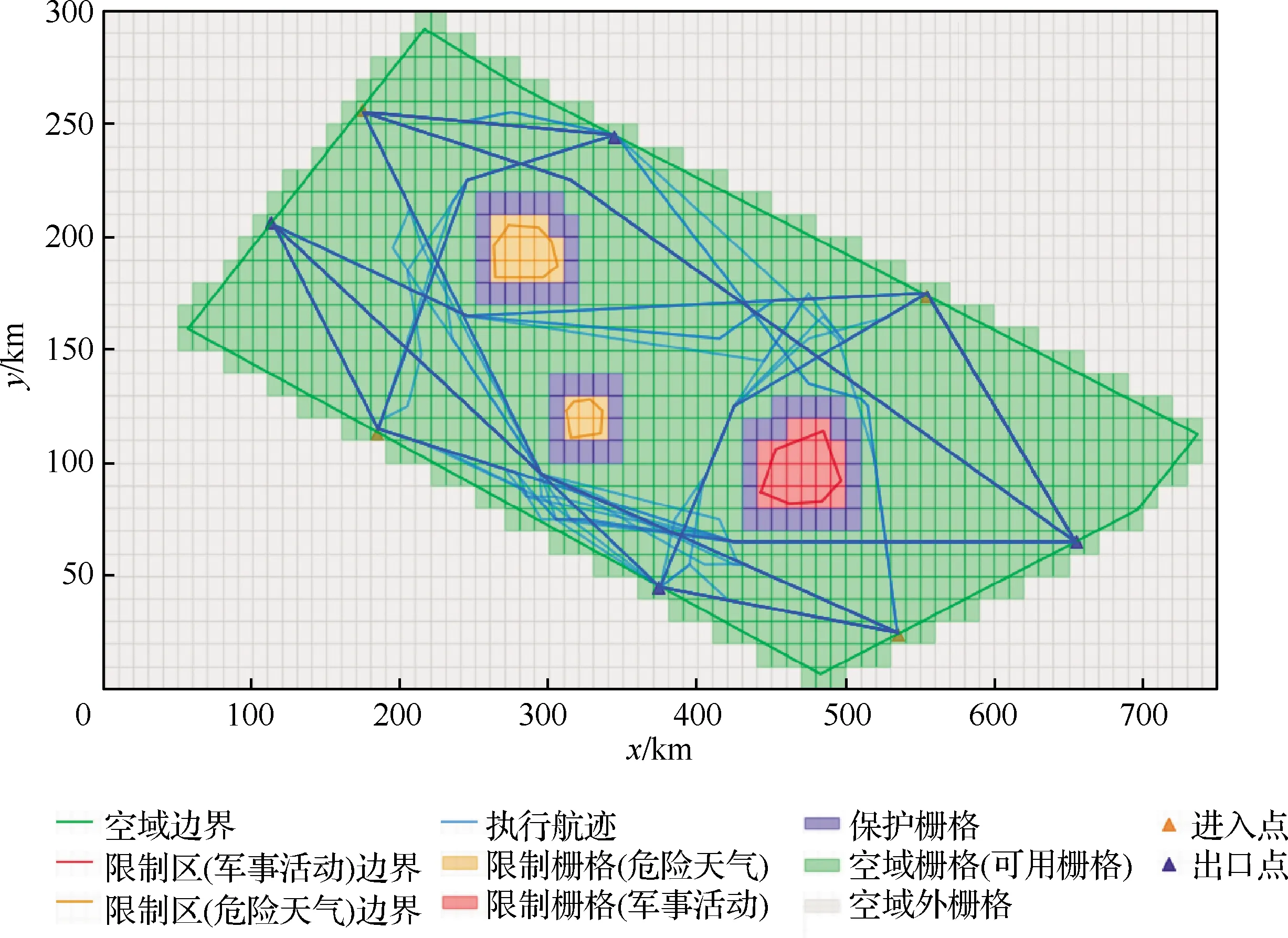
图12 执行航迹(平面维度)Fig.12 Executed trajectories (planar)

具体来说，图14展示了整个仿真过程中的每10 s的冲突数量与该空域中的瞬时交通量。为了规避与限制区以及其他航空器的冲突，部分航空器产生了一定程度的延误，这使得实际运行中的流量(期望航迹、执行航迹)要略高于计划的流量(商定航迹)。在运行过程中，交通流稳定在22架左右，最大为24架。绝大多数潜在冲突发生在空域中航空器数量超过20架的时候。显然，航空器数量的增加仍然是导致自主运行中产生潜在冲突的重要因素之一。

如上所述，因为受到航空器速度性能的限制，在复杂的运行中不可避免地会产生额外的飞行时间和距离。图15和图16展示了额外飞行时间分布，图17和图18展示了额外飞行距离分布，表1展示了仿真期间的统计数据。为了便于讨论，定义了如下参数，相关参数定义如表2所示。

图13 执行航迹(时空维度)Fig.13 Executed trajectories (temporal-spatial)

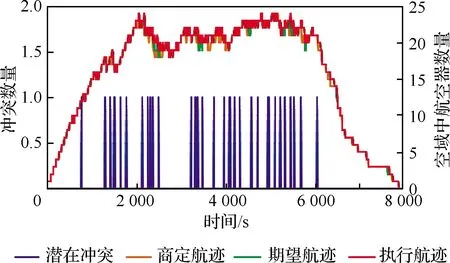
图14 冲突频率与瞬时交通量Fig.14 Frequency of conflicts and instantaneous traffic volume

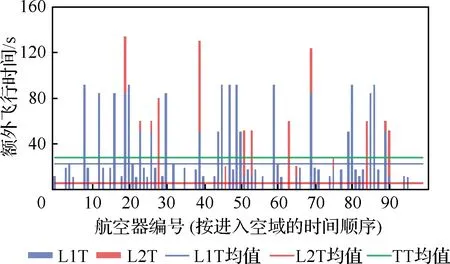
图15 额外飞行时间分布(数值)Fig.15 Extra flight time distribution (value)

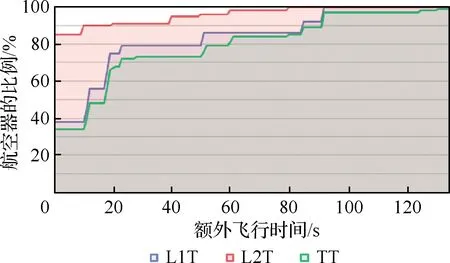
图16 额外飞行时间分布(累积)Fig.16 Extra flight time distribution (accumulation)

图17 额外飞行距离分布(数值)Fig.17 Extra flight distance distribution (value)

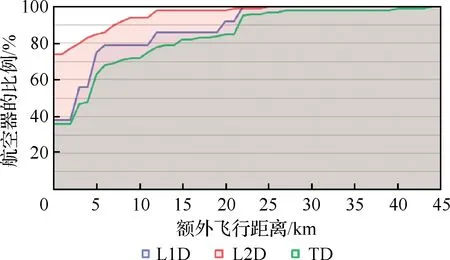
图18 额外飞行距离分布(累积)Fig.18 Extra flight distance distribution (accumulation)

L1T=tD-tA

L2T=tE-tD

TT=L1T+L2T=tE-tA

L1D=dD-dA

L2D=dE-dD

TD=L1D+L2D=dE-dA

(26)

需要说明的是，表1中，“均值”指所有航空器计算参数的均值，“数量”指受影响的航空器数量。所谓受影响航空器就是对应参数非零的航空器。例如，有62架航空器发生了L1T，那么关于L1T的受影响航空器的数量就是62。

在受影响的航空器中，73.3%的存在L2T的航空器发生了L1T。显然，因为商定航迹是无冲突的，航空器之间的潜在冲突是由限制区引起的。另一方面，这意味着只有17.7%的存在L1T的航空器发生了L2T。可能的原因有2个，一个是在运行中，当改航产生额外飞行距离时，航空器会通过加速来尽可能满足CTA要求。由数据可知，53.3%的存在L2D的航空器通过加速避免可能产生L2T。另一个原因，也从反方向证明了在调整阶段中航迹规划的有效性，即在航空器进入空域前，提前生成满足限制区约束的期望航迹不仅可以提前规避与限制区的冲突，而且也不会因此在运行阶段造成过多不可避免的延误。另外，关于受影响的航空器数量，L1T与L1D是相同的，TT与TD也是相同的。前者是因为商定航迹与期望航迹是基于相同的速度(经济航速)，L1D必定导致与之对应的L1T,而后者仅仅是因为巧合。

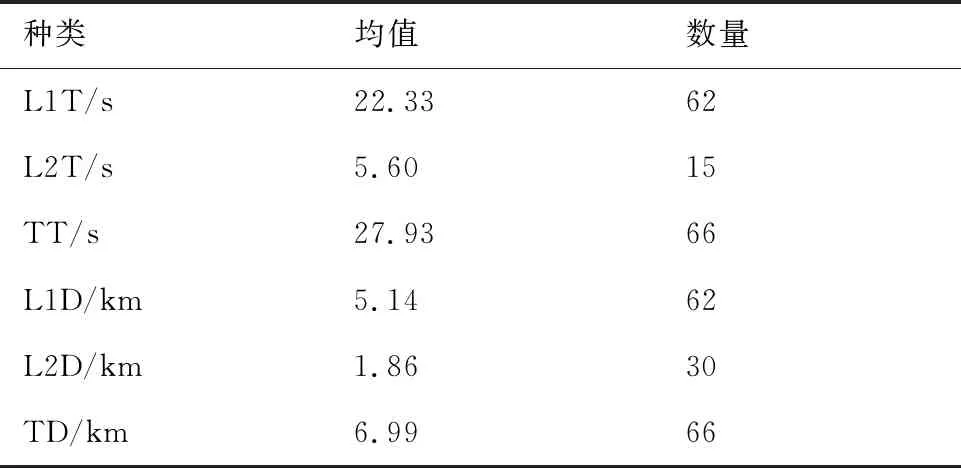
表1 数据分析Table 1 Data analysis

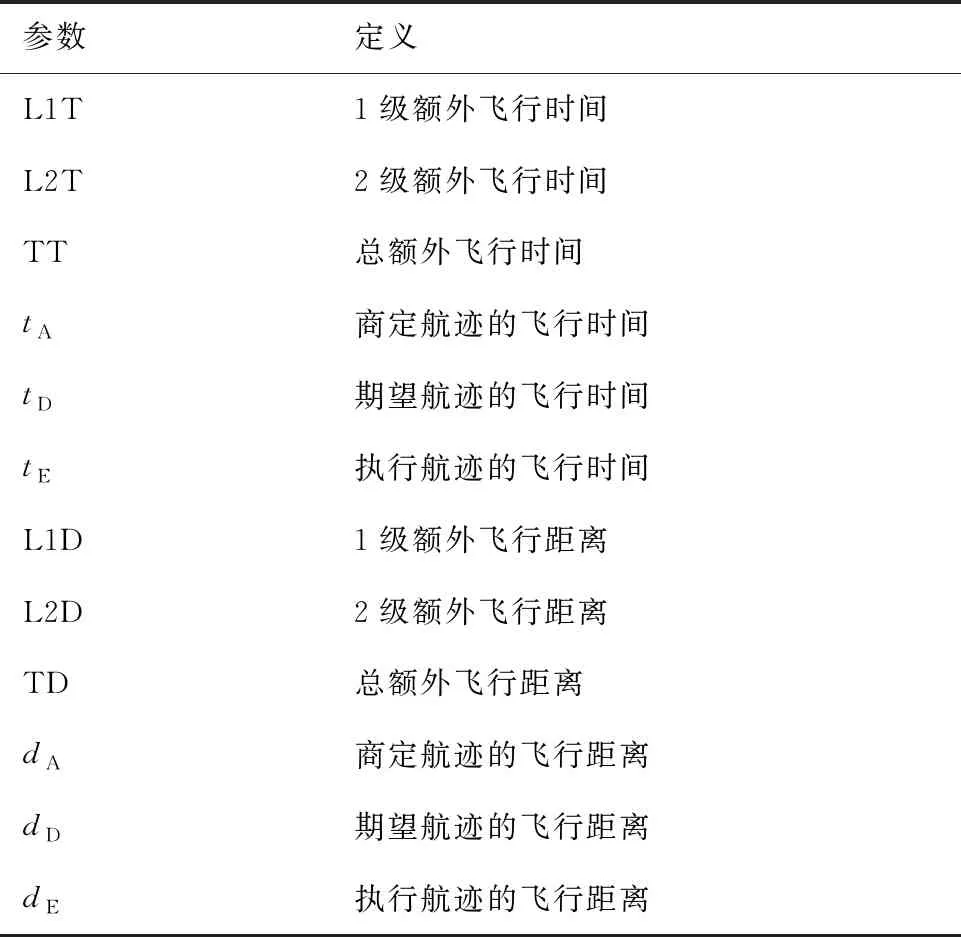
表2 参数定义Table 2 Parameter description

由于空域资源紧张，在高密度运行环境下，冲突解脱往往会导致额外的冲突产生，即多米诺效应(Domino Effect)。在解脱原理上，本文的解脱方法实际上是一对多的解脱，即在搜索改航路径时，确保可行改航路径是对探测范围内所有航空器的无冲突航迹，这从局部避免了多米诺效应的产生。从全局来看，研究中通常用多米诺效应指数(Domino Effect Parameter, DEP)来表征冲突解脱方法对空域稳定性的影响程度[46]。该指数表达式为

(27)

式中：C1为不执行冲突解脱时(本文中即按期望航迹飞行)空域中产生的冲突次数，C2为执行冲突解脱时(本文中即按执行航迹飞行)空域中产生的潜在冲突次数。本文中，C1为39，C2为35，故DEP为-0.10，其中C1与C2中相同的冲突有32个。一般来说，DEP为正数，本算例中DEP为负数，意味着该冲突解脱方法产生的额外潜在冲突的数量小于其在解脱前序潜在冲突时无形中消解的本该发生的后续潜在冲突的数量(本文中，前者为3次，后者为7次)。

事实上这是因为调整阶段是采用基于可视图的航迹规划，相同进出点的航空器得到的期望航迹的路径是相同的，故空域中的冲突多发生在各期望航迹的路径交汇点，相对集中。当一架航空器在同一交汇点附近先后与多架航空器存在潜在冲突时，当其第一次解脱后，就在一定程度上避开了这一交汇点，这使得其能有一定的概率避免随后本该出现在该交汇点附近的潜在冲突。

图19展示了本算例中全部3次额外潜在冲突。其中，原生冲突指由调整阶段的改航操作导致的潜在冲突；次生冲突指由运行阶段的改航操作导致的额外的潜在冲突；冲突时刻指该潜在冲突被探测到的时刻；进入时刻指该航空器进入本空域的时刻。例如，在2号额外潜在冲突中，39号航空器因探测到与35号航空器存在潜在冲突(该冲突在期望航迹中就已存在)，故进行改航操作，而此操作导致了其与46号航空器间产生了额外的潜在冲突(该冲突在期望航迹中不存在)。总的来说，本文方法不但从方法本身保证了局部不发生多米诺效应，也在全局保持一个较低的多米诺效应水平，甚至在某些情况下，前序冲突解脱无形消解了后续冲突。显然，从模型方法上，全局多米诺效应与探测范围具有直接关系，因此，如何动态根据空域内交通态势自适应调控探测范围是提升自主航迹运行稳定性的重要内容。

图19 多米诺效应分析Fig.19 Domino effect analysis

另外，航空器的机动频次亦是考察要素之一，因为过多的机动不但会增加运行风险和燃油消耗，亦会降低旅客舒适性。本文中，航空器改航由避让限制区和避让潜在冲突产生。阶段1基于可视图和最短路的航迹规划所产生的额外转弯次数主要由限制区尺寸和空间分布决定，本文设计的仿真场景较为复杂，仿真平均额外转弯次数为1.86；阶段2的额外转弯次数是由于冲突避让所产生，本文采用的是在保证航迹恢复情况下机动动作最少的解脱方法，即在一次冲突解脱中仅一架航空器进行一次改航规划，每次改航对应3个机动动作(出航、归航、航迹恢复)，阶段2平均额外转弯次数为1.05。由实验数据可知，在近2 h仿真过程中，在运行阶段，除了22,26,65,71,75这5架航空器进行了2次改航，其他进行解脱机动的航空器仅进行了1次改航。所以，本文方法以最少的机动解脱单次冲突，同时考虑到全局的多米诺效应也保持在较低水平(即全局冲突次数较少)，从而保证了航空器个体与总体的机动次数都处于较低水平。

除了上述有效性验证之外，计算成本也是衡量所提算法的效率和实用性的关键指标之一。图20 和图21分别展示了调整阶段中航迹调整的计算时间和运行阶段中冲突解脱的计算时间。本次仿真基于Intel(R) Core(TM) i7-10510U CPU @1.80GHz 2.30GHz和64位Windows10处理系统，采用了python3.8编程语言。在此计算环境下，航迹调整的平均计算时间为0.17 s，标准差为0.014 934 s；冲突解脱的平均计算时间为1.12 s，标准差为1.134 67 s。尽管冲突解脱的计算时间分布更为分散，但从统计角度来看，冲突解脱的计算时间与扇区的瞬时流量无关。但是，从优化算法的角度来看，当航空器遭遇潜在冲突时，计算时间对搜索空间的大小(潜在改航栅格数量)更为敏感。搜索空间越大，生成最优改航航路点所需要计算资源越多。

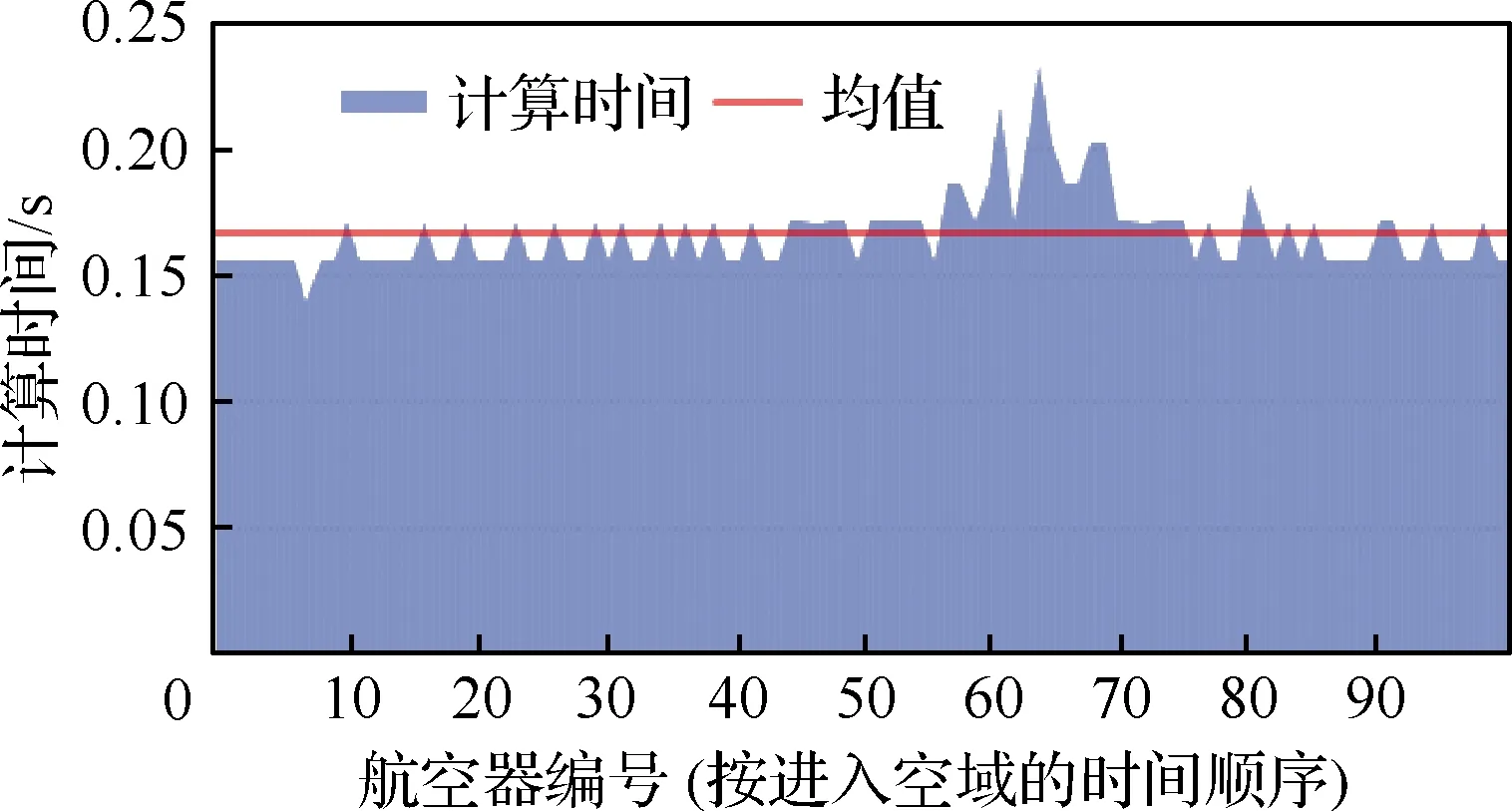
图20 航迹调整的计算时间Fig.20 Calculating time for trajectory modifications

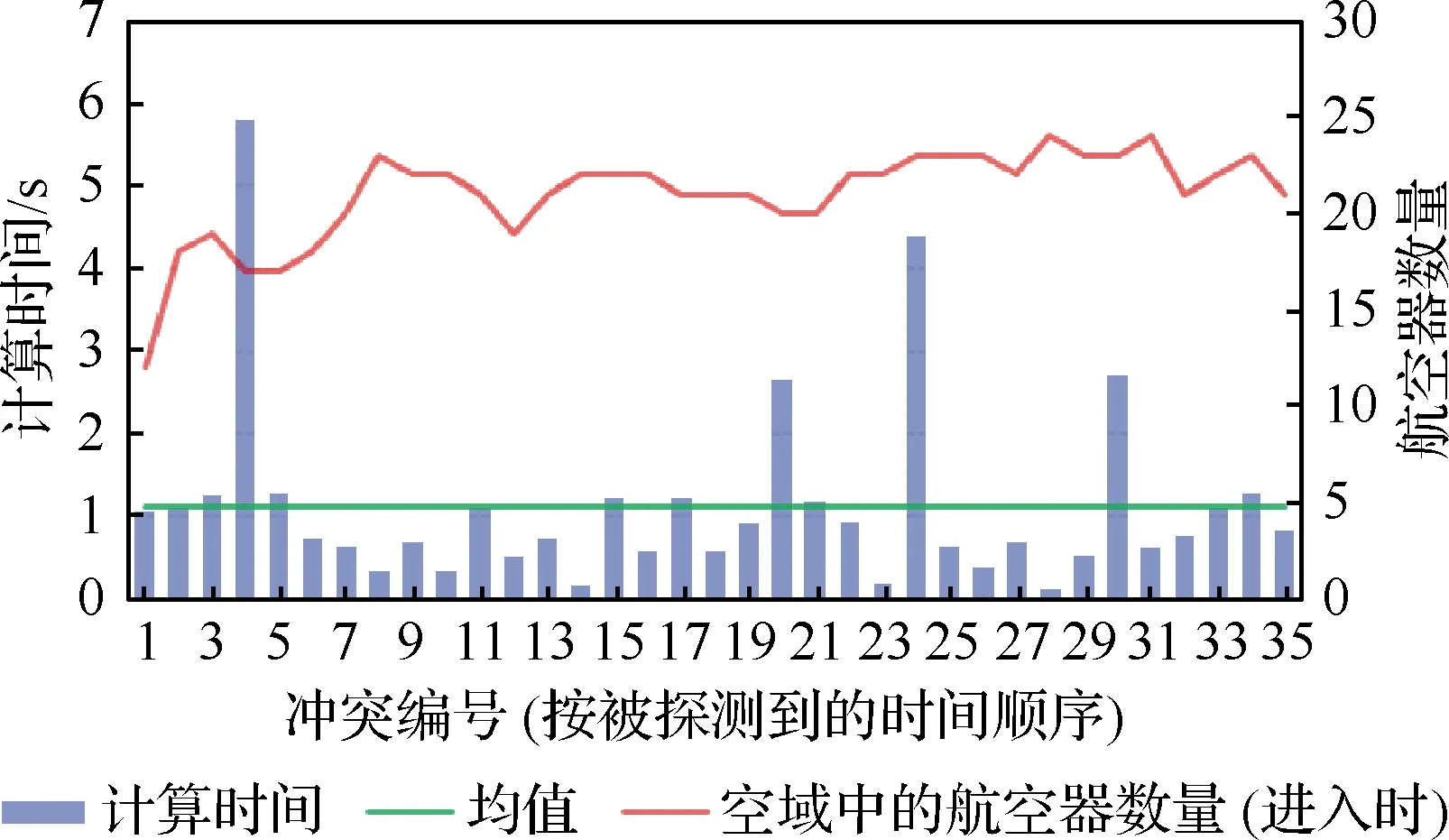
图21 实时冲突解脱的计算时间Fig.21 Calculating time for real-time conflict resolution

4.3 灵敏度分析

4.3.1 栅格尺寸

基于栅格的空域离散化是实现所提出的具有人机认知同步功能的实时自主四维航迹运行的第一步，也是关键的一步。如前文所述，可以通过增加导航和定位系统的性能来减小栅格的尺寸。我们进行了一系列关于栅格尺寸的灵敏度分析实验，研究讨论了栅格尺寸与运行性能(包括L2T、L2D、和潜在冲突数)、冲突解脱的平均计算时间之间的关系(详见图22和图23)。通过仿真实验，获取了栅格尺寸分别为0.625 km、1.25 km、2.5 km、5 km和10 km时的相关数据。应当指出，商定航迹、期望航迹、空域扇区、限制区和其他参数均保持不变。

结果表明，随着栅格尺寸的变化，L2T和L2D的总体趋势是非常接近的。运行效率在栅格尺寸为2.5 km处开始收敛，这意味着当栅格尺寸大于2.5 km时，随着栅格变大，L2T和L2D会显著增加。这是因为更大的栅格尺寸意味着更低的寻优精度，这导致寻优算法难以搜索到更好的可行解，从而对运行性能产生了负面影响。另外，随着栅格尺寸变小，潜在冲突的数量趋于减少。显然，优化精度的提高可以促进冲突的避免。

然而，如果栅格尺寸过小，那么过长的计算时间会抵消因寻优精度提高而带来的好处(详见图23)，最终导致运行性能略有下降。具体而言，当栅格尺寸减小到0.625 km时，冲突解脱平均计算时间超过2 min，这是不可接受的，尤其是对于高密度运行和发生特情的情况。这就说明，本文应当研究出合适的栅格尺寸，以便在计算成本和运行性能之间更好地做出权衡。

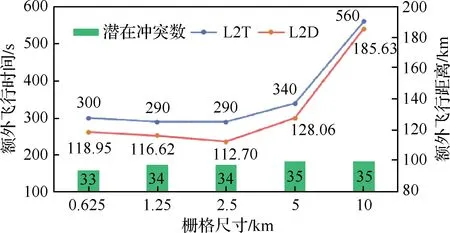
图22 栅格尺寸与运行性能/潜在冲突数Fig.22 Grid size vs operational efficiency/number of potential conflicts

图23 栅格尺寸与计算时间Fig.23 Grid size vs calculating time

4.3.2 探测范围

相比于全局冲突探测，局部冲突探测是减少单次探测时间和降低冲突解脱复杂度的重要手段。本文进行了一系列关于探测范围的灵敏度分析实验，研究讨论了探测范围与运行性能(包括L2T、L2D和潜在冲突数)、冲突解脱的平均计算时间之间的关系(详见图24和图25)。通过仿真实验，获取了探测范围(探测距离半径)从50 km到70 km(采样间隔1 km)的21组样本数据。与关于栅格尺寸的灵敏度分析实验类似，在此实验中，除了探测范围外其他参数均保持不变。

结果表明，随着探测范围增大，潜在冲突数有下降的趋势，这是因为更大的探测范围意味着更多的外部信息，从而能够更好地优化航迹以减少后续运行中的潜在冲突。随着探测范围增大，L2T与L2D也有减小趋势，即运行性能有增大的趋势。值得注意的是，从探测范围55 km到56 km 的数据发生了突变，这或许是因为潜在冲突的减少使得空域交通流的复杂性有所降低，从而提高了运行性能。

与上述趋势相反，随着探测范围的增大，冲突解脱的平均计算时间呈较为明显的上升趋势，这是因为探测范围的增大，使得航空器在每次调整航迹时，需要考虑更多的冲突约束，从而需要更多的计算资源。同样，值得注意的是，从探测范围55 km到56 km的数据出现了较大幅度与总体趋势相反的变化，这或许也是因为较低的交通流复杂性带来的增益效果。随着探测范围的变化，运行性能与冲突解脱的计算时间变化呈现出相反的趋势，这说明冲突探测范围同样值得进一步研究，以便在上述两者之中做出权衡。另外需要补充说明的一点是，由于冲突探测用时极短(平均每次冲突探测用间在0.000 2 s左右)，故在此不对其进行深入探讨。

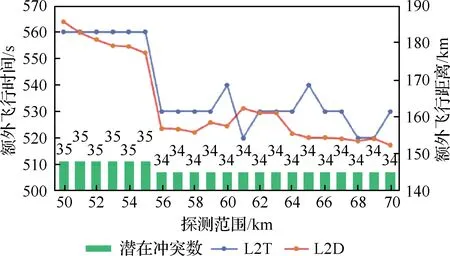
图24 探测范围与运行性能/潜在冲突数Fig.24 Detection range vs operational efficiency/number of potential conflicts

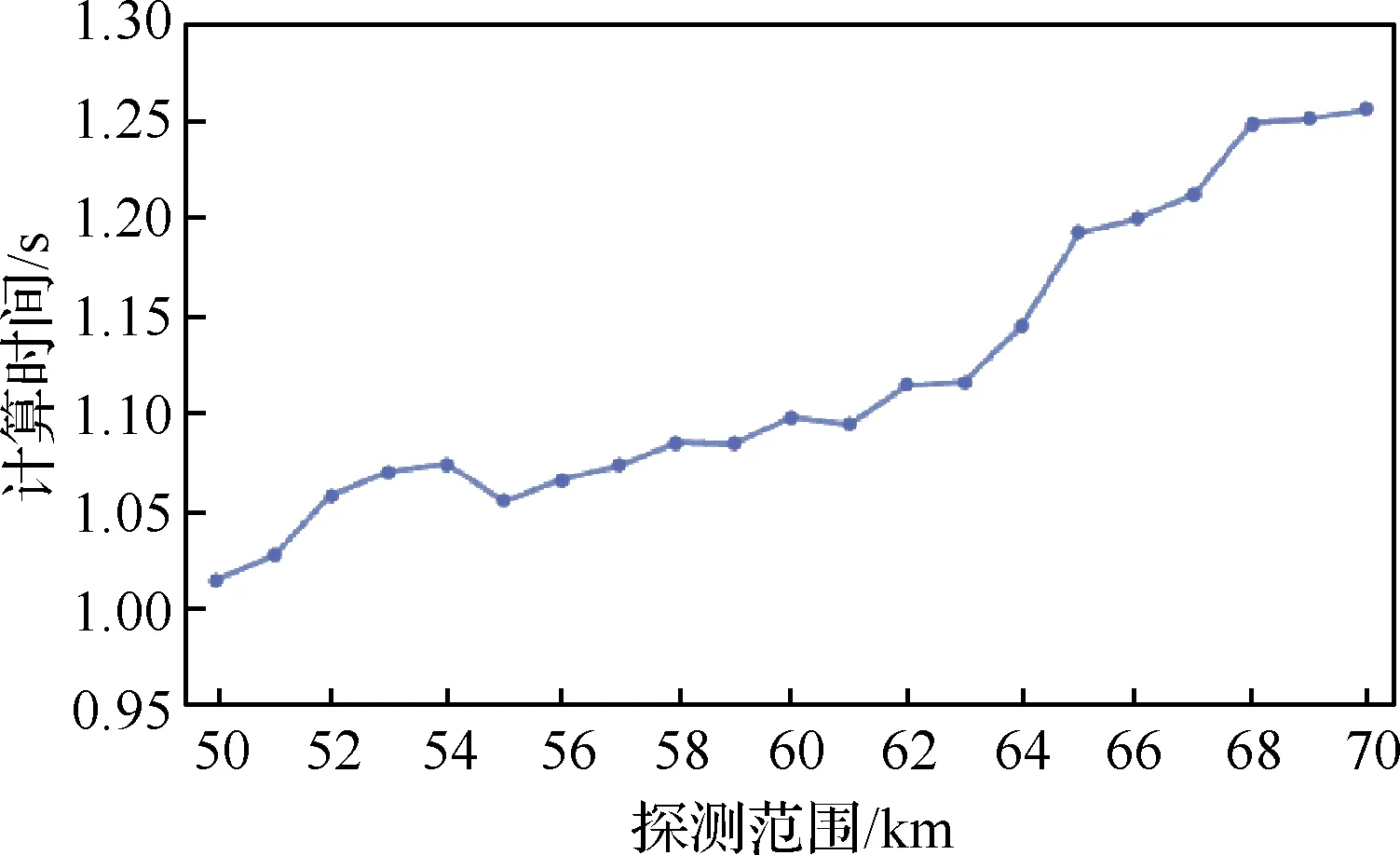
图25 探测范围与计算时间Fig.25 Detection range vs calculating time

5 结 论

本文提出了一种在受限空域中实时自主航迹冲突探测和解脱的方法。该方法致力于解决自主空管运行中的人机态势感知同步问题。为了实现这一愿景，首先，基于栅格的空域离散化使系统可以灵活地在优化精度和计算时间之间进行权衡。其次，通过运用可视图法和Dijkstra算法，使航空器能够快速生成期望航迹，从而在航空器即将进入空域时提前规避与限制区的冲突，以达到使运行阶段的计算资源可以集中使用在冲突解脱上的目的。最后，建立航迹时空可达域模型实现空地态势感知协同，运用局部探测解脱方法来降低冲突解脱的复杂性，同时也减少了单次冲突探测的时间。

通过基于中国西部典型空域的仿真算例验证了所提出方法的有效性。结果表明，该方法可以在存在限制区的空域中实现有效地冲突探测和解脱，同时保持较低的多米诺效应以及较少的改航次数。栅格尺寸和探测范围同时对冲突解脱计算时间和空域运行效率具有影响，且随着栅格尺寸或探测范围的变化，计算时间与运行效率呈现出相反的变化趋势。因此，优选合适的栅格尺寸和探测范围对于实现计算时间与运行效率之间科学权衡具有重要作用。在合适的栅格尺寸和探测范围下，期望航迹规划和实时冲突解脱的计算时间都在秒级，这表明该方法在战术级运行中具有较大潜力。

不确定性和多机协商是自主空中交通运行所面临的重要挑战。使本文框架能够有效支撑不确定航迹意图认知和基于可达时空域的轨迹协商，从而提升自主航迹运行的多维优化目标权衡，是本文后续研究重点，同时着力探究多高度层运行、动态环境因素、启发式航迹协商算法，以期构建安全、高效、公平、绿色的自主航迹运行体系。