航天器太阳圆面速度差/太阳视方向组合导航

宁晓琳，黄玉琳，晁雯

1. 北京航空航天大学 前沿科学技术创新研究院，北京 100083 2. 北京航空航天大学 仪器科学与光电工程学院，北京 100083

深空探测是中国航天白皮书中的一项占有极高地位的规划任务，而天文导航是航天器在执行深空探测任务时的一种有效自主导航方法，拥有成本低、自主性强、误差不积累等优势[1]。现有的天文导航方法根据所使用天文量测信息的不同，大致可分为3类：利用天体敏感器提取天体角度信息的天文测角导航[2-6]、测量脉冲信号TOA提取距离信息的天文脉冲星测距导航[7-9]及利用光谱仪测量相对多普勒速度信息的天文光谱测速导航[10-12]。每一种导航算法都有其各自的特点与局限性，寻找一种新的天文量测信息以及新的导航技术是非常有价值的。

多年来各国都在开展对于太阳的探索[13-17]，随着科技进步，对于太阳的了解也越来越深入。早在1612年，Galileo就通过观察太阳表面的黑子的活动发现太阳是自转的。Howard和Harvey通过光谱观测，发现太阳表面存在较差自转[18]。随后，一些国内外学者对太阳较差自转模型及其随时间的变化进行了研究[19]。这些研究表明太阳的较差自转导致太阳不同点的速度是不同的。太阳多普勒速度是一种重要的量测量[20]，目前已有的基于太阳多普勒速度导航方法中通常都是将太阳看作一个点，而实际上，探测器观测到的太阳是一个圆盘，并且探测器从不同的角度观测到的太阳圆面上不同位置处的多普勒速度也是不同的。这一速度信息与航天器的位置之间存在可建模的数学关系，从而可以作为量测量估计航天器的位置信息。为了消除测量误差和太阳自身不稳定造成的误差，本文提出将太阳圆面上相隔180°的2个对径点的太阳圆面多普勒视向速度的差值，简称太阳圆面速度差作为天文量测信息，其几何本质是提供了一个探测器的位置圆锥。在此基础上，将太阳圆面速度差和太阳视方向进行组合，提出了一种基于太阳圆面速度差/太阳视方向的组合导航新方法。

本文基于太阳圆面速度差/太阳视方向的组合导航方法的基本原理，首先介绍了太阳的较差自转和太阳圆面上不同点的多普勒速度的计算公式，其次阐述了太阳圆面速度差的获取和几何意义以及太阳圆面速度差与太阳视方向的互补性，量测量的获取与模型建立，然后给出了基于太阳圆面速度差/太阳视方向的组合导航方法的系统模型，最后通过仿真证明了基于太阳圆面速度差/太阳视方向的组合导航方法能有效提升导航性能。此外，本文还对影响导航精度的主要因素，包括光谱仪精度、采样周期和光谱仪数量进行了详细分析。

1 太阳较差自转和太阳圆面上不同点的多普勒速度

1.1 太阳较差自转

有学者通过观察太阳黑子，太阳光谱等建立了太阳较差自转速率模型，并对其随时间的变化进行了研究，结果表明太阳较差自转导致太阳圆面上不同点的速度不同[21-22]。太阳表面自转速率随纬度的变化而变化，其较差自转率可表示为

ω=a+bsin2φ+csin4φ

(1)

式中：ω为太阳上某一点的角速度，单位是(°)/d；φ为该点的纬度；a、b、c为常值，单位是(°)/d，a=14.713±0.049，b=-2.396±0.188，c=-1.787±0.253[23]。

由式(1)可得太阳圆面上的不同点的自转线速率为

v=ωRscosφ=(a+bsin2φ+csin4φ)Rscosφ

(2)

式中：Rs=6.955×105km为太阳半径。

1.2 太阳圆面上不同点的多普勒速度

如图1所示，在日心惯性空间直角坐标系O-xyz中，太阳圆面上M点的经度和纬度分别为β、φ。

图1 日心惯性空间直角坐标系Fig.1 Heliocentric inertial space rectangular coordinate system

则速度v在太阳视方向上的投影速度vr大小为

(3)

2 太阳圆面速度差的获取和几何意义

2.1 太阳圆面速度差的获取

如图2所示，在探测器上安装4个光谱仪SpA、SpB、SpC、SpD，并使其光轴与四棱锥的4条棱一致，S为太阳探测器质心，S′为四棱锥底面外接圆的圆心，δ为光谱仪光轴与四棱锥中心轴线的安装角，R为四棱锥底面外接圆的半径，h为四棱锥的高，可以得到

(4)

在太阳质心坐标系下利用4个光谱仪可测量得到太阳圆面上2组相互垂直的点A、B、C、D的速度分别为vA、vB、vC、vD。

经过计算可以得到4点之间的速度差值分别为δAB=vA-vB,δAC=vA-vC,δAD=vA-vD,δBC=vB-vC,δBD=vB-vD,δCD=vC-vD。

设量测量Zk=[δAB,δAC,δAD,δBC,δBD,δCD]。

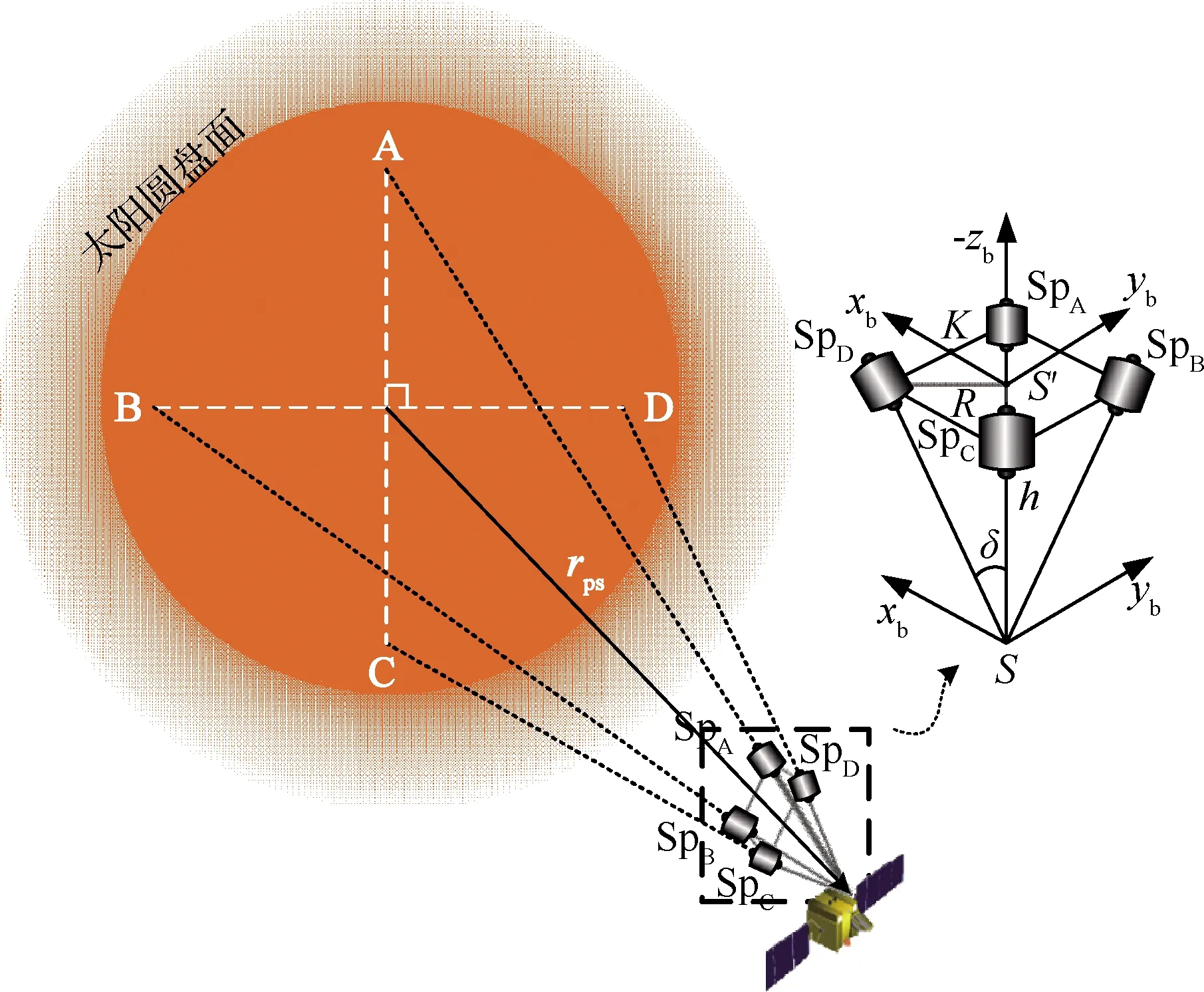
图2 光谱仪测量太阳圆面上的多普勒速度Fig.2 Measurement of Doppler velocity on the Solar disk by spectrometer

2.2 太阳圆面速度差的几何意义

如图1所示，在日心惯性空间直角坐标系中，∠MOL=α，θ为太阳自转轴和太阳视方向的夹角，称为太阳自转轴观测角。为了简化证明，进行坐标变换，令x，y轴绕z轴旋转，使得rps位于yz平面内，则太阳视方向可表示为rps=[0,sinθ,cosθ]T，M点的速度v在太阳视方向上的投影速度vr大小可表示为

vr=v·rps=vcosβsinθ

(5)

(6)

则太阳圆面上相差180°的两点处的投影速度差为

(7)

在球面直角ΔMLN中，sinφ=sinαsinθ，将其代入式(7)，结合式(1)，可得

dv=2Rscosαsinθ(a+bsin2αsin2θ+csin4αsin4θ)

(8)

对于太阳圆面上2组互相垂直的点，可以得到2个速度差dv1、dv2，且α∈(-π,π)，θ∈(0,π)。由式(8)可得

(9)

将光谱仪测量得到的数据dv1、dv2代入式(9) 便可解算出太阳自转轴观测角θ和α。

通过太阳自转轴观测角θ，可知探测器必位于以太阳为顶点，以θ为锥心角的圆锥面上(如图3所示)，也即太阳圆面速度差的几何意义。

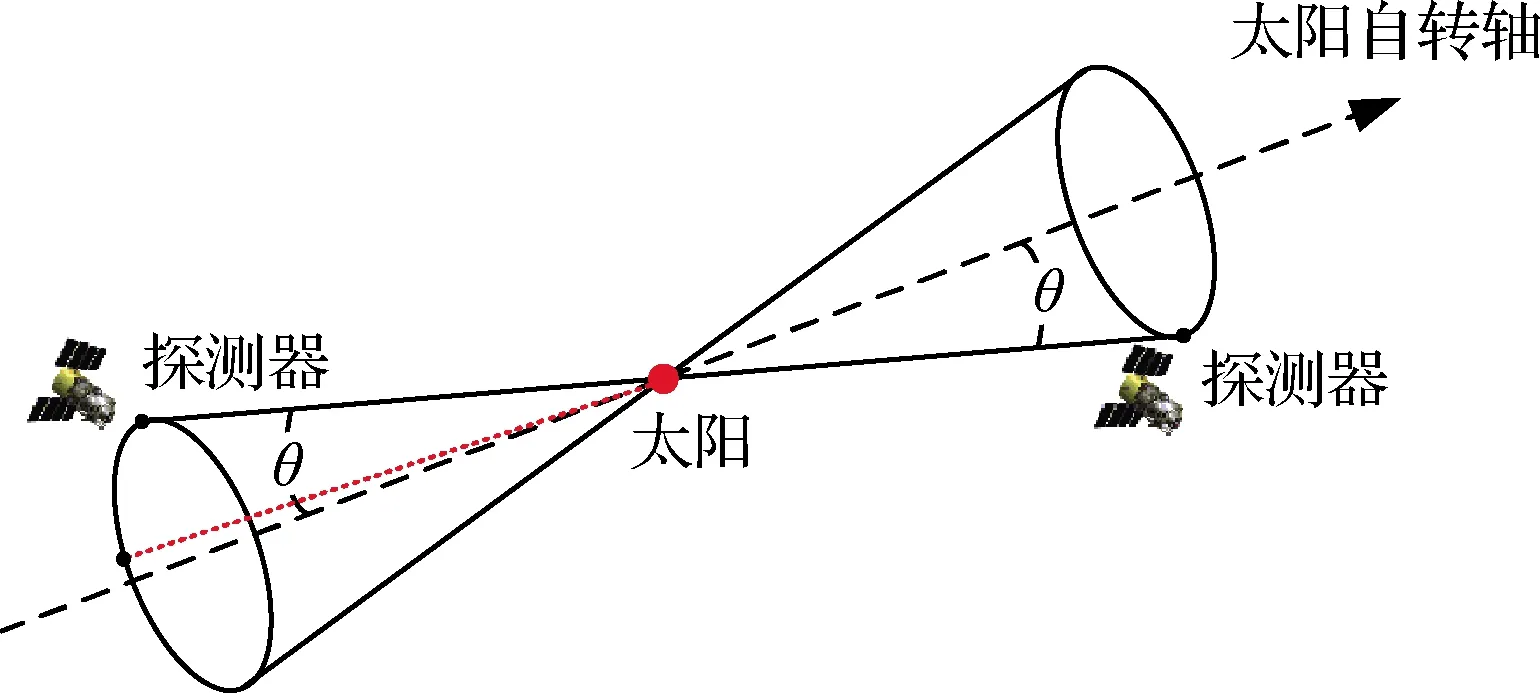
图3 探测器的位置信息Fig.3 Location information of solar explorer

2.3 太阳圆面速度差与太阳视方向的互补性

从2.2节可以看出，太阳圆面速度差可确定一个探测器的位置圆锥，但仅靠这一信息，单次观测不能完全确定探测器的位置，虽然可以通过连续观测，结合轨道动力学确定探测器的位置，但会影响收敛速度。利用太阳敏感器可测量得到太阳方向的量测量，即太阳的高度角与方位角，从而确定探测器是在上述圆锥的哪一条锥线上。

3 基于太阳圆面速度差/太阳视方向的组合导航方法

基于太阳圆面速度差/太阳视方向的天文组合导航方法，其系统模型以探测器轨道动力学方程为基础，并采取卡尔曼滤波技术[24]来估计探测器的具体位置和速度信息。本节给出了该方法的状态模型与量测模型。

3.1 状态模型

太阳探测器的运动方程可看作一个二体模型，其以太阳为中心天体[25]。在太阳质心坐标系下状态模型可表示为

(10)

式中：rps、vps为探测器相对太阳的位置、速度矢量；μs为太阳的引力常数；w1为过程噪声。

设状态量为Xk=[rps，vps]T，过程噪声为Wk-1，则太阳质心惯性坐标系下的状态模型式(10) 可简写为

Xk=f(Xk-1,T)+Wk-1

(11)

式中:T为采样时间。

3.2 量测模型

3.2.1 太阳圆面速度差的量测模型

以太阳圆面速度差为量测量的量测模型主要包括以下4个重要步骤：

1) 计算A、B、C、D 4点在探测器本体坐标系下的位置矢量

对于本体坐标系S-xbybzb，其原点位于探测器的质心。设本体坐标系下光谱仪指向太阳圆面上的A、B、C、D 这4点的方向矢量分别为

(12)

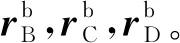
2) 计算A、B、C、D 4点在太阳惯性系下的经度和纬度

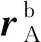
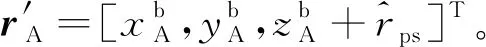
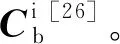
(13)

(14)

(15)

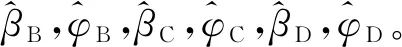
3) 计算太阳惯性系下太阳圆面上不同点的多普勒速度

4) 计算太阳圆面上不同点的多普勒速度差值

为了消除光谱仪自身误差及太阳自身速度的影响，以太阳圆面速度差为量测量，其可记作

(16)

综上，基于太阳圆面速度差的新型天文导航方法的量测模型可由式(14)～式(16)计算得到

(17)

式中：h1(·)为步骤1～步骤4的整个计算过程；V1,k为量测噪声。

3.2.2 太阳视方向的量测模型

以太阳视方向，即高度角η与方位角φ作为量测量时的量测模型可以写为

(18)

式中：vη、vφ为量测噪声。

设Z2,k=[η,φ]T，量测噪声V2,k=[vη,vφ]T，则以太阳视方向为量测量的传统天文导航方法的量测方程为

Z2,k=h2(Xk)+V2,k

(19)

式中:h2( )为太阳视方向量测量的非线性量测函数。

3.2.3 基于太阳圆面速度差/太阳视方向的组合导航

设基于太阳圆面速度差/太阳视方向的组合导航方法的量测量Z3,k=[Z1,k,Z2,k]T，量测误差V3,k=[V1,k,V2,k]T，则基于太阳圆面速度差/太阳视方向的组合导航方法的量测模型可写为

Z3,k=h3(Xk)+V3,k

(20)

式中:h3( )为组合系统的非线性量测函数。

结合无迹卡尔曼滤波(Unscented Kalman Filter，UKF)方法即可估计探测器的导航信息。基于太阳圆面速度差/太阳视方向的组合方法的流程如图4所示。

图4 太阳圆面速度差/太阳视方向组合导航方法整体结构图Fig.4 Overall structure of integrated navigation method of solar disk velocity difference and sun direction

4 仿真和分析

4.1 仿真条件

以太阳探测器为例进行仿真分析，仿真数据由STK (Systems Tool Kit)[27]产生。坐标采用J2000.0日心惯性坐标系，其长半轴a=1.07×107km，偏心率e=0.02，轨道倾角i=60°，升交点赤经为0°，近地点角距为0°。全部仿真时间为2个周期的时间。

光谱仪精度为0.1 m/s[28]，光谱仪与日心矢量夹角δ=3.7°，太阳敏感器精度为28″[1]，滤波周期为300 s。

4.2 仿真结果

利用UKF滤波方法对基于太阳圆面速度差/太阳视方向的组合导航方法进行仿真分析，并与仅使用太阳圆面速度差作为量测量和仅使用太阳视方向作为量测量的导航方法进行了比较分析。

4.2.1 3种量测量的导航结果比较

图5、图6和图7分别给出了仅以太阳圆面速度差作为量测量、仅以太阳视方向作为量测量和以太阳圆面速度差/太阳视方向组合作为量测量的导航结果。表1给出了太阳圆面速度差、太阳视方向和太阳圆面速度差/太阳视方向3种量测量的导航方法滤波收敛后的仿真平均结果。仿真结果的统计时间段从第9天开始至结束。

图5 太阳圆面速度差为量测量的导航结果Fig.5 Navigation results of using measurement of velocity difference of solar disk

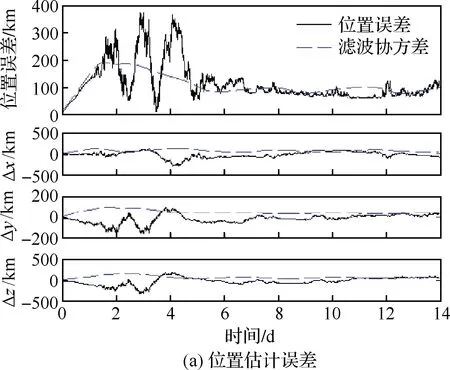
图6 太阳视方向为量测量的导航结果Fig.6 Navigation results of using measurement of sun direction

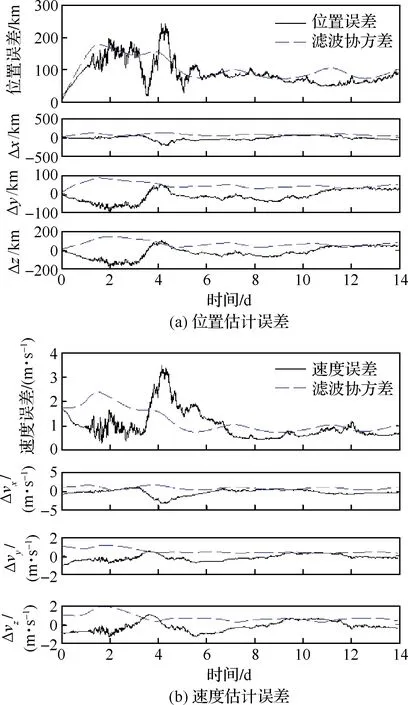
图7 太阳圆面速度差/太阳视方向为量测量的导航结果Fig.7 Navigation results of using measurements of solar disk velocity difference and sun direction

由图5可知，仅以太阳圆面速度差作为量测量时，估计误差从第3天开始逐渐收敛且最大位置误差低于300 km。由图6可知，仅以太阳视方向作为量测量时曲线波动较大，最大位置误差近400 km。由图7可知，以太阳圆面速度差/太阳视方向作为量测量的组合导航方法曲线较为平缓且收敛性较好。由表1可知，3种方法中基于太阳圆面速度差/太阳视方向的组合天文导航方法的导航性能最好，精度相比较于单独用太阳圆面速度差或太阳视方向作为量测量的导航方法分别提升了10.2%和16.0%。

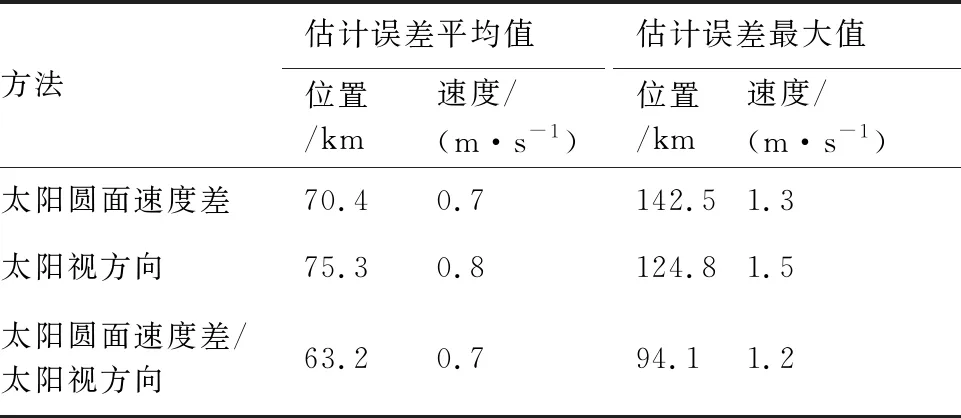
表1 3种方法的导航结果Table 1 Navigation results of three measurements

4.2.2 影响因素分析

在本节中，对基于太阳圆面速度差/太阳视方向组合导航方法在不同影响因素下的导航性能进行了仿真分析，包括光谱仪精度、采样周期长短和光谱仪数量。仿真条件如4.1节所示。

1) 光谱仪精度对导航结果的影响

图8和表2给出了在采样周期为300 s，光谱仪数量为4的情况下，光谱仪精度分别为0.01 m/s，0.1 m/s，1 m/s，10 m/s，100 m/s时滤波收敛后的仿真平均结果。可见随着光谱仪精度的降低，导航性能也在变差，当光谱仪的精度低于100 m/s时，基于太阳圆面速度差/太阳视方向的导航方法位置估计误差会发散。

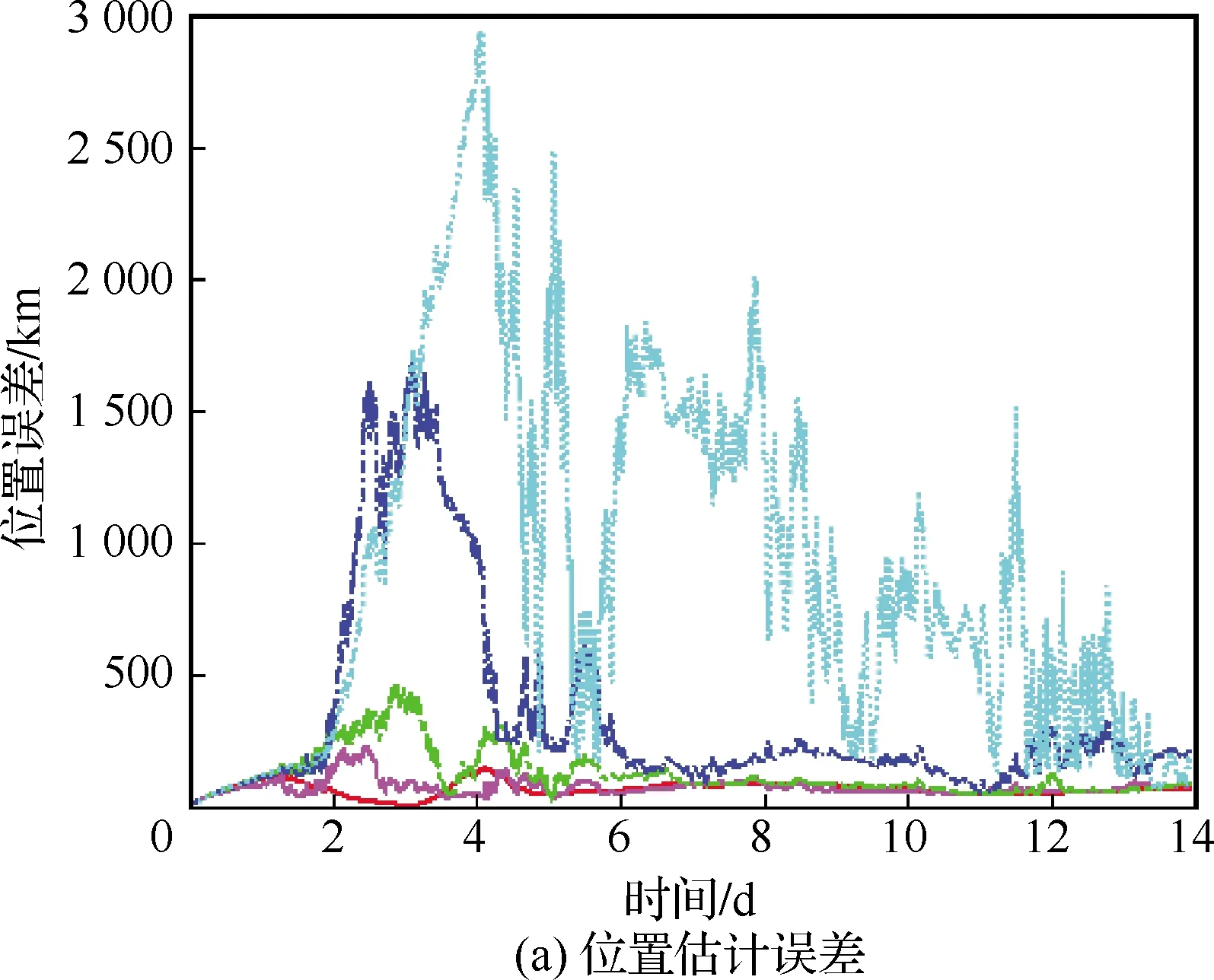
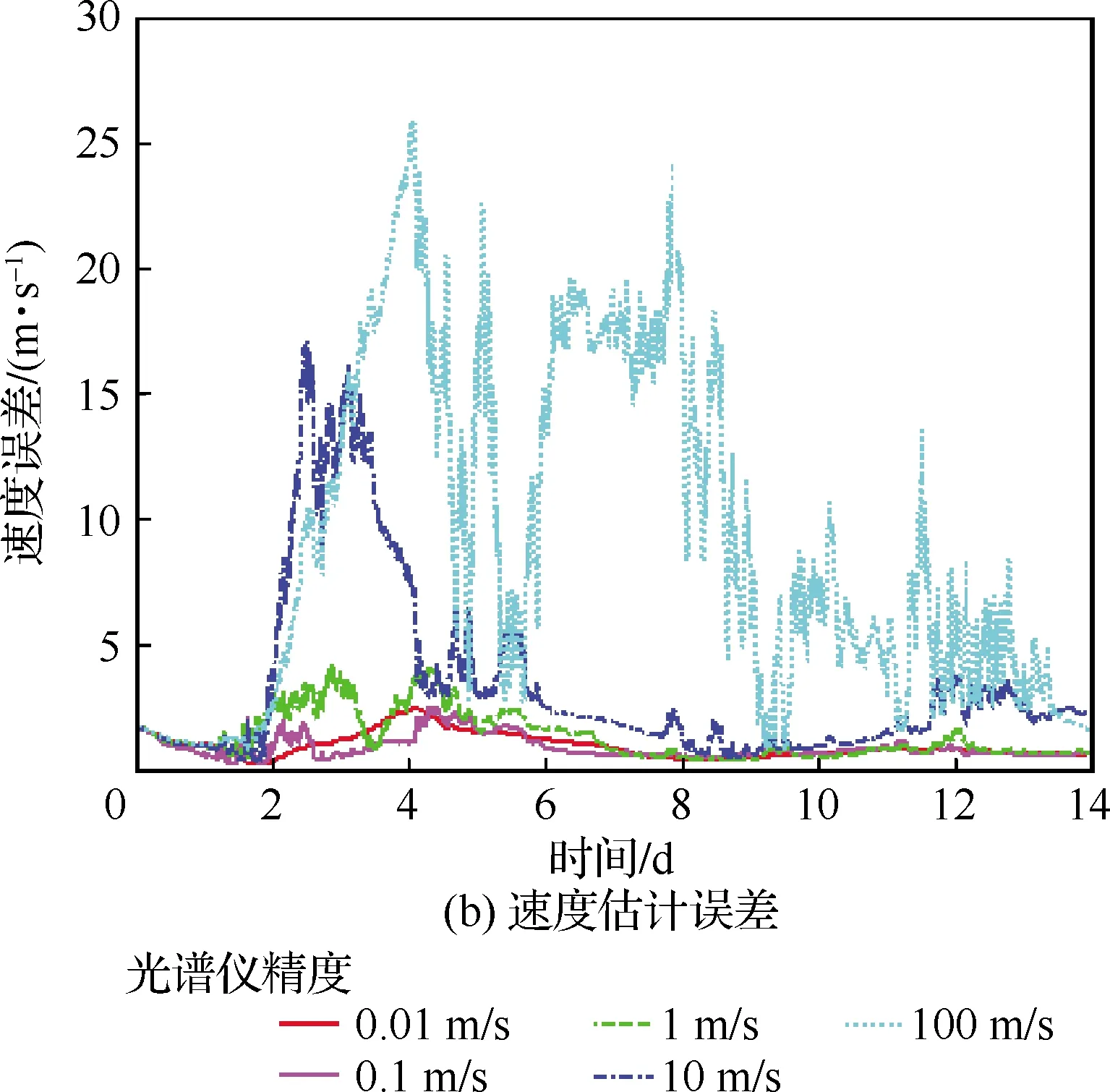
图8 不同光谱仪精度对基于太阳圆面速度差/太阳视方向组合天文导航方法的影响Fig.8 Impact of different spectrometer precision on integrated celestial navigation method based on velocity difference of solar disk and sun direction

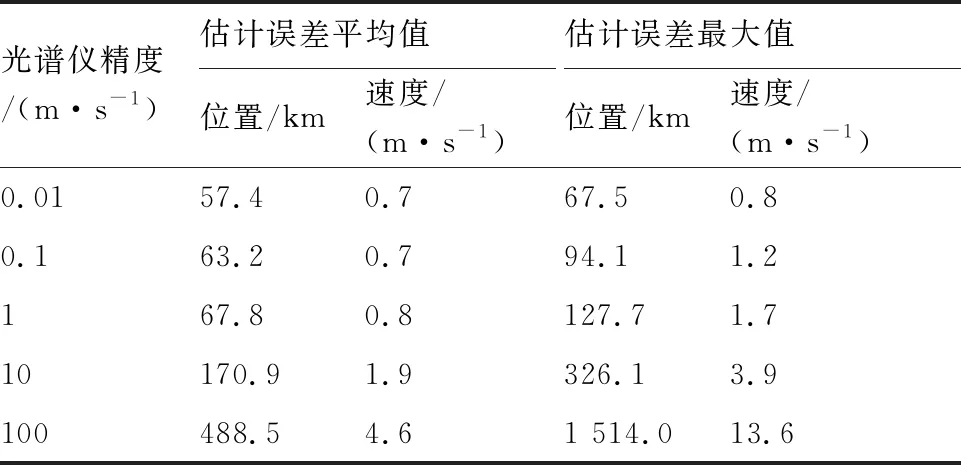
表2 不同光谱仪精度的导航结果

2) 采样周期对导航结果的影响

图9和表3给出了在光谱仪精度为0.1 m/s，光谱仪数量为4的情况下，采样周期分别为60 s，120 s，300 s，600 s，900 s时滤波收敛后的仿真平均结果。可见采样周期越短导航性能越好，随着采样周期的缩短，精度提升的速度也在变慢，因此调整采样周期的长短对导航估计精度的提高是有限的。当采样周期较长时，导航结果所受影响较大，原因是系统轨道动力学模型的线性化误差较大，致使系统的性能下降。当采样周期大于300 s时，估计误差曲线波动幅度变大，导航性能较差。

3) 光谱仪数量对导航结果的影响

图10和表4给出了在光谱仪精度为0.1 m/s，采样周期为300 s的情况下，光谱仪的数量分别

图9 不同采样周期对基于太阳圆面速度差/太阳视方向组合天文导航方法的影响Fig.9 Impact of different sampling time on integrated celestial navigation method based on velocity difference of solar disk and sun direction

表3 不同采样周期的导航结果

为2，3，4，量测量数量分别为1，3，6 时滤波收敛后的仿真平均结果。可见光谱仪的数量越多，位置估计误差越小。这是由于光谱仪数量越多，所获取的量测量数量越多，提供的量测信息越多，导航结果越好，但由于成本要求，精度的提高有限。

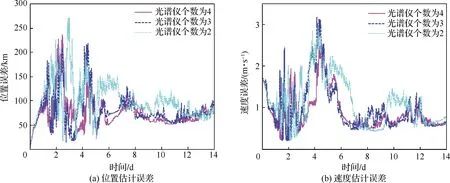
图10 不同光谱仪数量对基于太阳圆面速度差/太阳视方向组合天文导航方法的影响Fig.10 Impact of different number of spectrometers on integrated celestial navigation method based on velocity difference of solar disk and sun direction

表4 不同光谱仪数量的导航结果

5 结 论

1) 本文提出了一种新的太阳圆面速度差天文量测量，并在此基础上进一步提出了太阳圆面速度差/太阳视方向的组合导航新方法。利用太阳圆面速度差和太阳视方向互补的特性，将2种量测量结合起来，提高导航性能。仿真结果证明，相比较于使用单一的太阳圆面速度差和太阳视方向导航方法，太阳圆面速度差/太阳视方向组合导航方法能有效提升导航性能。

此外，在对组合导航进行影响因素分析时，可以看到在一定条件下，组合导航性能随着光谱仪精度的降低而变差，随着采样周期的缩短与光谱仪数量的增加而提升。因此，在实际应用中，应根据具体需求，选择合适的光谱仪精度、采样周期与光谱仪数量。

2) 本文在使用信息融合算法进行组合导航时，使用了传统的无迹卡尔曼滤波方法，且仿真实验中仅对组合导航与单一量测量导航间的性能进行了对比研究，后续会根据需求和问题的深入分析对滤波算法，该方法与其他量测信息的特点比较进行更深入的研究。