电流信号加窗处理对频谱性能的影响

2020-12-01谢志平郭子义郎彦城

贵州师范大学学报（自然科学版） 2020年6期

谢志平，郭子义，郎彦城，王蕾

(1.贵州师范大学机械与电气工程学院，贵州贵阳 550001；2.贵州师范大学大数据与计算机科学学院，贵州贵阳 550001；3.贵州师范大学经济与管理学院，贵州贵阳 550025)

0 引言

针对直流微电机生产线上质量检测无法实现自动化检测的问题，文献[1-2]提出了一种基于直流微电机电枢电流的故障检测方法，该方法需用快速傅里叶变换(FFT)处理电枢电流信号，获取电流信号的频谱特性，利用频谱故障多特征量对电机进行故障诊断。在实际应用中难以实现对时域电流信号进行整周期截断和同步采样，必然会引起频谱泄露和栅栏效应[3-5]，影响电流故障多特征量值的准确度，因此有必要研究减小频谱泄露和栅栏效应的方法。

通过加sine窗函数[4]、加Hanning自卷积窗[6]、加频移算法[7]、新型窗函数和插值结合方法[8]等可以减小频谱泄漏。对电流信号进行加窗处理时，窗函数类型对电流的频谱质量影响较大[9-10]，因此合理选择窗函数在信号处理过程中尤为重要。本文在推导电流信号加窗后快速傅里叶变换表达式基础上，分析了电流信号加各种窗函数对频谱性能的影响，并比较了不同采样点数和采样频率对电流频谱特性的影响，给出了在直流微电机故障诊断中窗函数、采样点数和采样频率的选择依据。

1 电流信号加窗分析

直流微电机的数学模型为[1,2]：

(1)

式中u、e、i、r和Lm分别表示电枢电压、电枢感应电势、电枢电流、电枢电阻和电枢电感；T、T0和T1分别表示电磁转矩、空载转矩和负载转矩；ω表示电机角速度，J表示电机转动惯量。

在电机稳定运行状态下，电枢电流ia(t)可由式(1)求出[1]：

(2)

式中Ia和Iam分别表示电枢电流的直流分量和幅值；c、k、p、m和φa分别表示系数、换向片数、极对数、转速和相位角。

ia(t)=Ia+Iamsin(2πf0t+φa)

(3)

对ia(t)以采样频率fs，则得离散时间信号为

ia(n)=Ia+Iamsin(2πf0n/fs+φa)n=0,1,…,N-1

(4)

对ia(n)加窗函数，则加窗序列iaw(n)为

iaw(n)=ia(n)w(n)

(5)

式中常见窗函数w(n)有矩形窗、汉宁窗、哈明窗、布莱克曼窗、三角窗和巴特利特窗。

加窗序列iaw(n)的连续傅立叶变换为

(6)

式中WR(·)为窗函数的离散傅里叶变换。

对式(6)进行离散抽样，忽略负频点处频峰的旁瓣影响，得到加窗后信号的离散傅里叶变换的表达式:

(7)

式中：离散抽样间隔为Δf=fs/N，N为数据截断长度，k为抽样频点的序号。

因信号的非整周期截断和非同步采样，信号的频率kΔf很难正好位于抽样频点上，即一般不是整数。各离散点上的FFT频谱与信号的理想谱不一致，就会产生泄漏。通过改变窗长和窗函数类型就可以控制能量泄漏。

2 信号的加窗FFT分析

根据良品直流电机测试结果可知[1]，电枢电流可近似表示为i(t)=(33+10sin1180πt)(mA)。利用上矩形窗、汉宁窗、哈明窗、布莱克曼窗、三角窗和巴特利特窗对良品直流电机的电枢电流信号先进行加窗，再进行FFT变换。根据奈奎斯特定理，采样频率设为40 960，采样点数为1 024点。利用Matlab可以得到图1所示的加各种窗函数的电流信号频谱特性。

由图1可知，加汉宁窗和加哈明窗旁瓣衰减最快，布莱克曼窗衰减很慢，矩形窗旁瓣较高但主瓣最窄，巴特利特窗和三角窗的旁瓣最多。加不同的窗函数对电枢电流的频率特性影响较大，为定性比较各种窗函数之间的差异程度，因此，定义不同窗函数直流幅值、正弦幅值和频率的误差率为：

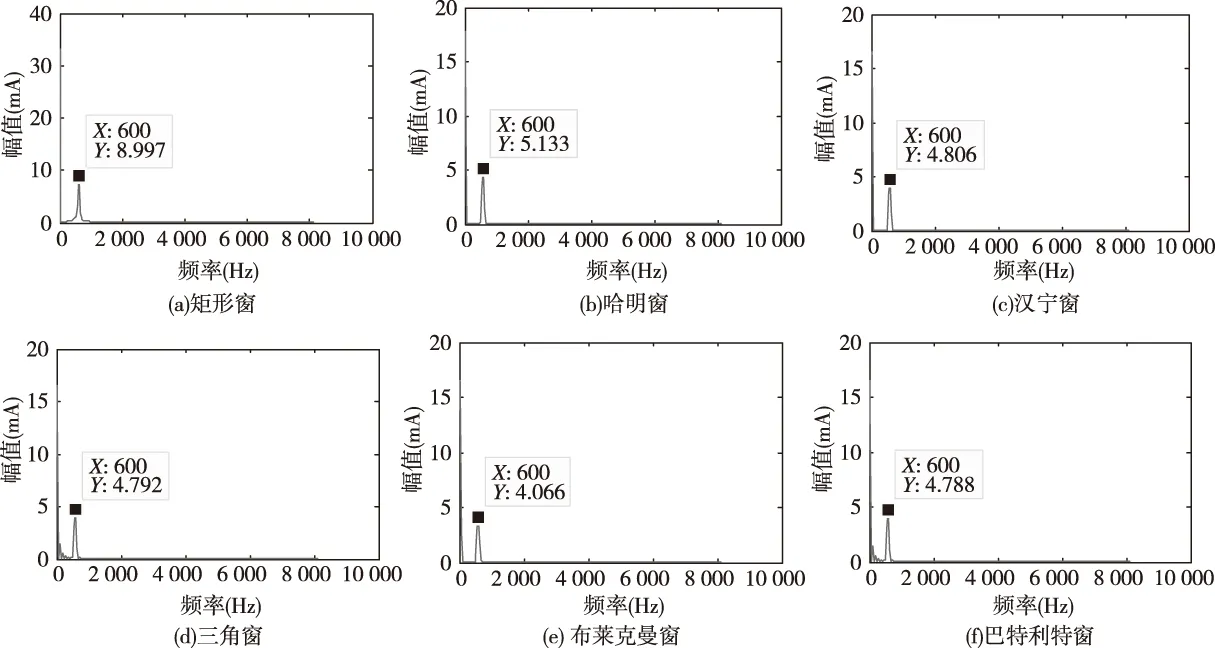
图1 加各种窗函数的电流信号频谱特性Fig.1 The spectrum performance of current signal adding various window functions

(8)

式中i=直流幅值，正弦幅值，频率；j=矩形窗，汉宁窗，哈明窗，布莱克曼窗，三角窗，巴特利特窗；aij表示加不同窗函数后的直流幅值、正弦幅值和频率；hi分别表示电枢电流实际的直流幅值、正弦幅值和频率。各种加窗函数的幅值和频率误差率如表1所示。

表1 加各种窗函数的误差率Tab.1 Error rate of adding various window functions

由表1可知，加布莱克曼窗的直流幅值误差和正弦幅值误差最大，加巴特利特窗和加三角窗次之，其次是加汉宁窗和加哈明窗，最小的是加矩形窗。6种窗函数的频率误差相同。通过对比分析6种加窗函数的误差率，在电枢电流频谱分析中应选用矩形窗作为加窗函数。

3 采样点数分析

选择不同的采样点数会影响到计算时间和计算精度，采样点的数目并不是越多越好，而是要以最少的采样点数达到最佳目的。对电枢电流信号进行加矩形窗处理，采样点数分别选取为256点、512点、1 024点和2 048点，其对应的频谱特性如图2所示。由图2可知，采样点数为256的矩型窗函数的主瓣宽度最宽；采样点数为512的矩型窗函数的主瓣宽度较点数为256的要窄些；采样点数为1 024的矩型窗函数的主瓣宽度最窄且旁瓣衰减很快；采样点数为2 048的矩型窗函数的旁瓣衰减较慢。

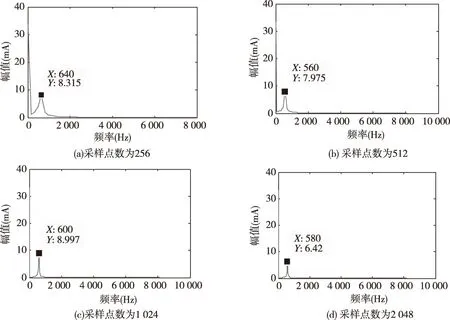
图2 采样点数不同的电流信号频谱特性Fig.2 The spectrum performance of current signal with various sampling number

为定性比较不同采样点数之间的差异程度，因此，定义不同采样点的直流幅值、正弦幅值和频率的误差率εij为：

(9)

式中i=直流幅值，正弦幅值，频率；j=256，512，1 024，2 048；bij表示加不同采样点的直流幅值、正弦幅值和频率。不同采样点的直流幅值、正弦幅值和频率的误差率见表2。采样点数越多，直流幅值、正弦幅值和频率的误差率越小，但采样点数为2 048时，正弦幅值误差率偏大是由于频点600 Hz出现幅值为6.313的旁瓣。综上所述，为保证计算速度和计算精度，选用矩形窗对电枢电流信号进行截断处理，其采样频率选用40 960 Hz，采样点数为1 024点。