含有Riesz-Feller位势的非线性变阶分数阶Lévy-Feller扩散方程的全隐差分格式

吴 春,刘冬兵

(1.重庆师范大学 数学科学学院，重庆 401331;2.攀枝花学院 数学与计算机学院,四川 攀枝花 617000)

0 引言

本文考虑如下的含有Riesz-Feller位势的变阶非线性分数阶Lévy-Feller扩散方程:

(1)

1 全隐式的有限差分格式

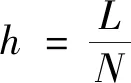
(2)

(3)

将式(2)和式(3)代入方程(1)可得到如下的差分格式:

(4)

(5)

格式(4)可改成如下的形式:

(6)

2 全隐式有限差分格式的稳定性和收敛性

定理1 假设方程(1)的解u(x,t)是充分光滑的,则当τ充分小时,全隐差分格式(4)～(5)是稳定的。

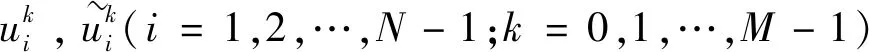
(7)

≤‖Ek‖∞+τL‖Ek+1‖∞

(8)

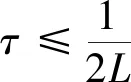
(9)

因此,全隐差分格式(4)～(5)是稳定性的。

定理2 在定理1的条件下,差分格式(4)～(5)的解依L∞-范数收敛到方程(1)的解,收敛阶为O(τ+h)。

(10)

(11)

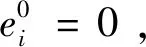
‖ek+1‖∞≤(1+2τL)‖ek‖∞+C1τ(τ+h)≤(1+2τL)2‖ek-1‖∞+C1τ(τ+h)[(1+2τL)+1]≤(1+2τL)k+1‖e0‖∞+C1τ(τ+h)[(1+2τL)k+…+1]≤C1τ(τ+h)(ke2LT)=O(τ+h)

(12)

故定理2得证。

3 数值例子

考虑如下的变阶非线性分数阶Lévy-Feller扩散方程:

取定时间步长τ=0.000 1,空间步长h=0.02。图1是t=0.01时刻由全隐差分格式(4)计算得到的数值解与精确解的平面图,可以看出数值解收敛于精确解。图2是全隐差分格式(4)计算得到的数值解与空间轴、时间轴之间的三维立体图。

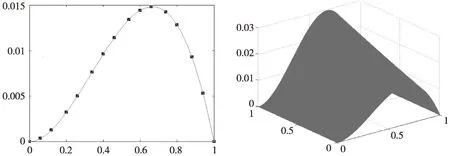
图1 数值解与精确解比较图 图2 三维立体图Fig.1 Comparison for numerical and exact solution Fig.2 Stereoscopic graphics

表1 在T=1时差分格式的误差及收敛率Tab.1 Error and convergence rate of difference scheme when T=1

从图1和表1可以看出，本文所提出的全隐式有限差分格式求解含有Riesz-Feller位势的非线性变阶分数阶Lévy-Feller扩散方程是可靠的和有效地。