对国家标准GB/T 9239.21—2019的解析与评价

郭卫建，郭晓雯，焦振峰

(1.北京双元天衡检测科技有限公司，北京 100085；2.北京理工大学 机电学院，北京 100081)

1 引 言

平衡机是用于检测回转机械零件(本文后称作转子)不平衡量的仪器，广泛应用于汽车、航天、能源、通用等工业领域。测量精度是平衡机的一个重要指标。GB/T 9239.21—2019《机械振动 转子平衡 第21部分：平衡机的描述与评定》是对平衡机精度检测的国家标准，此国家标准等同采用了国际标准ISO 21940-21：2012 《Mechanical vibration-Rotor balancing- Part 21: Description and evaluation of balancing machines》。该国际标准1975年第一次发布，采用了两个精度指标“最小可达剩余不平衡量(Minimum Achievable Residual Unbalance)，Umar”和“不平衡量减少率(Unbalance Reduction Ratio)，URR”。在过去的45年里，该国际标准虽经历了3次更新，但一直沿用Umar和URR两个指标。

我国采用该国际标准，先后发布了相应的平衡机国家标准。GB/T 9239.21—2019是最新版的国家标准，已于今年5月1日起实施。本文对新实施的国家标准中Umar、URR进行详尽解析，以期帮助相关人员准确理解和评价该标准。

2 Umar和URR检测实例

下面通过实例，按国家标准[1]对选定的平衡机进行Umar和URR检测。

2.1 选取校验转子和试验质量

对一台选定的平衡机进行检测前，需要选取一个校验转子(Proving Rotor)和一组试验质量(Test Mass)。

2.1.1 校验转子的选取

被检测平衡机为一台卧式硬支撑平衡机，最大承载转子重量20kg。校验转子的质量应在平衡机承载质量容量范围下1/3以内。按国家标准[1]推荐的卧式平衡机检测用B型内质心校验转子的尺寸、质量和最高转速，选用质量为5kg的B型校验转子。

图1为校验转子外形图。校验转子的主要尺寸为：校验转子中间圆柱体半径41mm，试验平面间距离B1、B2都为41mm，转子放到平衡机上时，支撑位置为轴颈Ⅰ，Ⅱ处。

图1 B型校验转子示意图

2.1.2 试验质量的选取

试验质量用于在校验转子的试验平面上产生规定的不平衡量。被检测的平衡机所标称的最小可达剩余不平衡度为emar=0.2g·mm/kg，标称的不平衡量减少率URR为95%。

对应的Umar为emar乘以校验转子的质量：

Umar=0.2g·mm/kg×5kg=1g·mm

测量平面1和测量平面2上每面最小可达剩余不平衡量Umar per plane都为一半的Umar，即：

Umar per plane=Umar/2=0.5g·mm

试验质量为圆柱状，如图2所示，中心有螺孔，长度为6mm。假定试验质量的质心在形心上，当把试验质量拧到校验转子的外圆表面的螺柱上时，试验质量的质心离校验转子的回转轴线的距离为：R1=R2=41mm+3mm=44mm。对应Umar=1g·mm的不平衡量，试验质量m1应为：

m1=1g·mm/44mm=0.02273g

图2 试验质量示意图

进行Umar检测，需要一个10倍Umar的试验质量(m10)，m10=0.2273g，产生的不平衡量为10g·mm。进行URR检测，国家标准[1]规定，固定试验质量产生20Umar～60Umar，移动试验质量为5倍的固定试验质量。本实例中采用固定试验质量m30产生30Umar，移动试验质量m150产生150Umar，则有：

m30=0.6818g，m150=3.409g，其产生的不平衡量分别为30g·mm和150g·mm。

2.2 最小可达剩余不平衡量的检测及评定

2.2.1 试验准备

(1)对平衡机进行调整，设定试验平面的半径R1，R2为44mm，设定支撑位置Ⅰ、Ⅱ与测量平面的距离A、B、C分别为41mm、82mm、41mm，选定测量转速1200r/min。

(2)将校验转子每一平面的剩余不平衡量平衡到小于5Umar。本实例中，平衡结果为试验平面1平衡到1.9g·mm/150°，试验平面2平衡到1.2g·mm/45°。

(3)在校验转子上再加上两个不平衡质量(采用橡皮泥)，每个不平衡质量产生5至10倍Umar。加装后测量值如表1中第一行所示。

表1 校验转子的平衡记录表

(4)对转子进行4次平衡检测，并在校验转子的两个端面平面上进行不超过4次校正，读数(测量值)如表1所示。

(5)将平衡机的相角基准改变60°后，校验转子的不平衡量测量值如表1中最后一行所示。

2.2.2Umar检测

按任意顺序将试验质量m10依次加在试验平面3的所有螺柱上，运行平衡机，测量转子试验平面1和试验平面2上的不平衡量，并把测量值记录在表2中，只记录不平衡量大小，不记录角度。

2.2.3Umar评定

(1)计算：求出每个读数除以其所对应平面的12个测量值的“平均值”的倍数，并将其记录在表2中。

表2 Umar检测记录表

(2)绘制曲线图：将计算出的值(倍数)绘制成图，如图3所示。

(3)界线：图3中的水平中位线表征每个平面读数的算术平均值，两条虚线(0.88和1.12)表征每个平面算术平均值的±12%的限值界限。

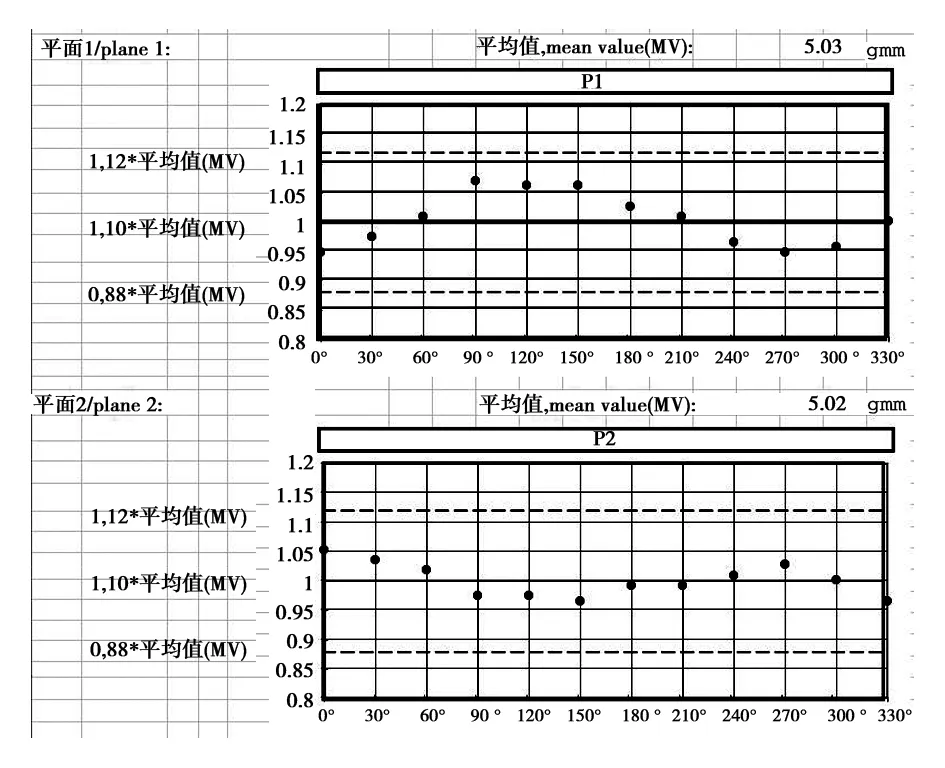
图3 Umar检测评定图

(4)评定：如果平衡机在检测后满足所有的标绘点均在两条虚线(0.88和1.12)给定的范围之内，允许有一点超出，则认为该平衡机已经通过了Umar的检测，即已达到了标称的最小可达剩余不平衡量。本检测实例平面1和平面2所有的标绘点都在两条虚线(0.88和1.12)之内，平衡机通过了Umar的检测。

2.3 不平衡量减少率URR检测及评定

2.3.1 试验准备

按国家标准[1]的要求，除非Umar检测完成后立即进行URR检测，否则要进行Umar检测前的准备工作。本实例是在做完Umar检测后立即进行URR检测。

2.3.2 URR检测

在试验平面1上，将一个固定试验质量m30加装在0°，在试验平面2上，将另一个固定试验质量m30加装在90°。在平面1其余的11个位置中选择30°位置作为移动试验质量m150的起始位置，在平面2其余的11个位置中选择60°位置作为移动试验质量m150的起始位置。平面1上的移动质量每次增加30°间隔；平面2上的移动质量每次减少30°间隔。共进行11次平衡操作，检测并记录测量值，并将两个平面的测量值记录在表3中。将各个测量值除以固定试验质量的不平衡量值，求出倍数并记录到表3中。

按表3中倍数及对应的角度，描述到图4所示的URR评定图中。评定图是由11组同心的URR极限圆组成。从里向外，各层同心圆表征URR的限值分别为95%、90%、85%和80%。极限圆的圆心和半径按表4的数据绘制。

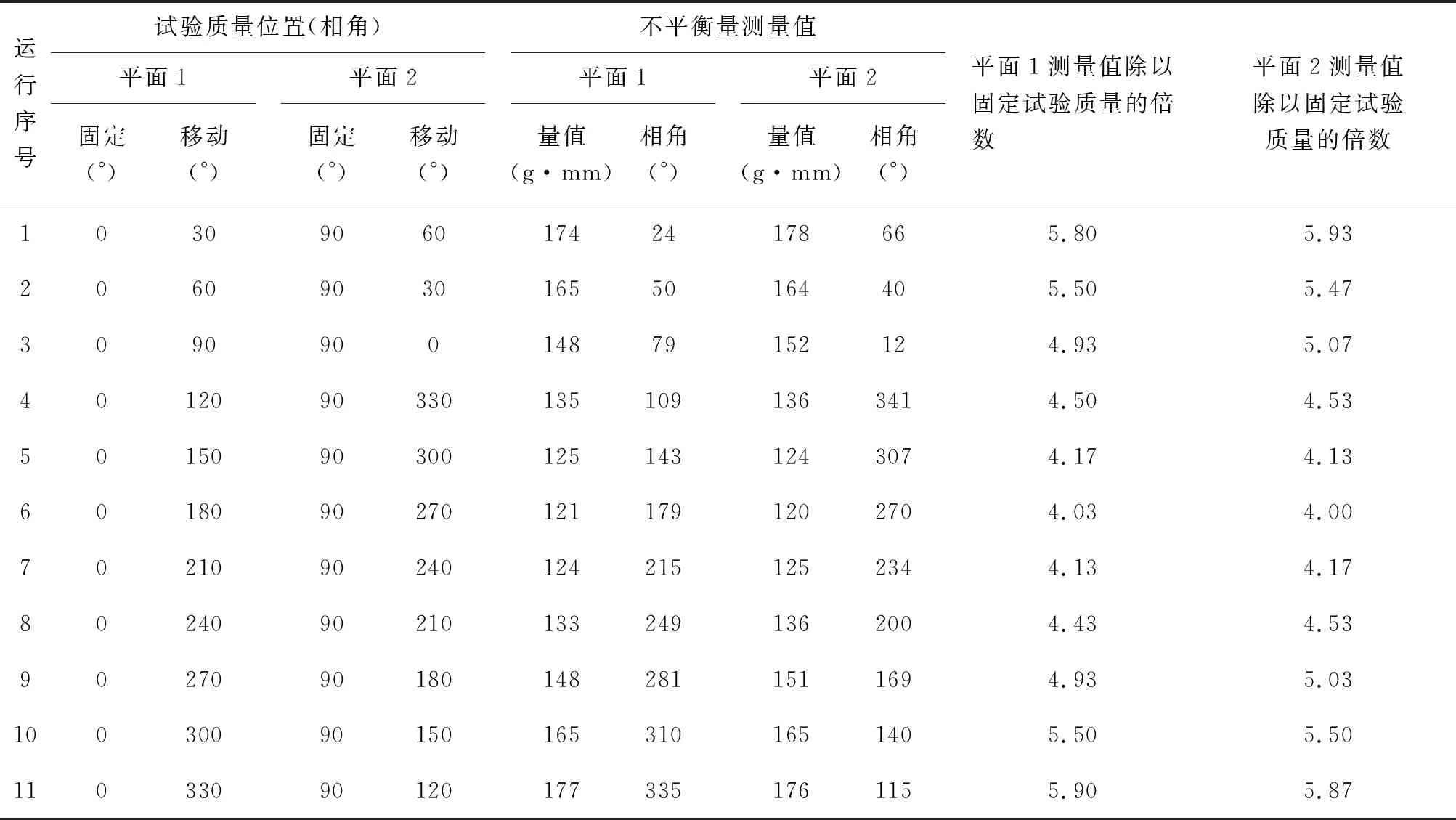
表3 双面试验用URR检测记录表

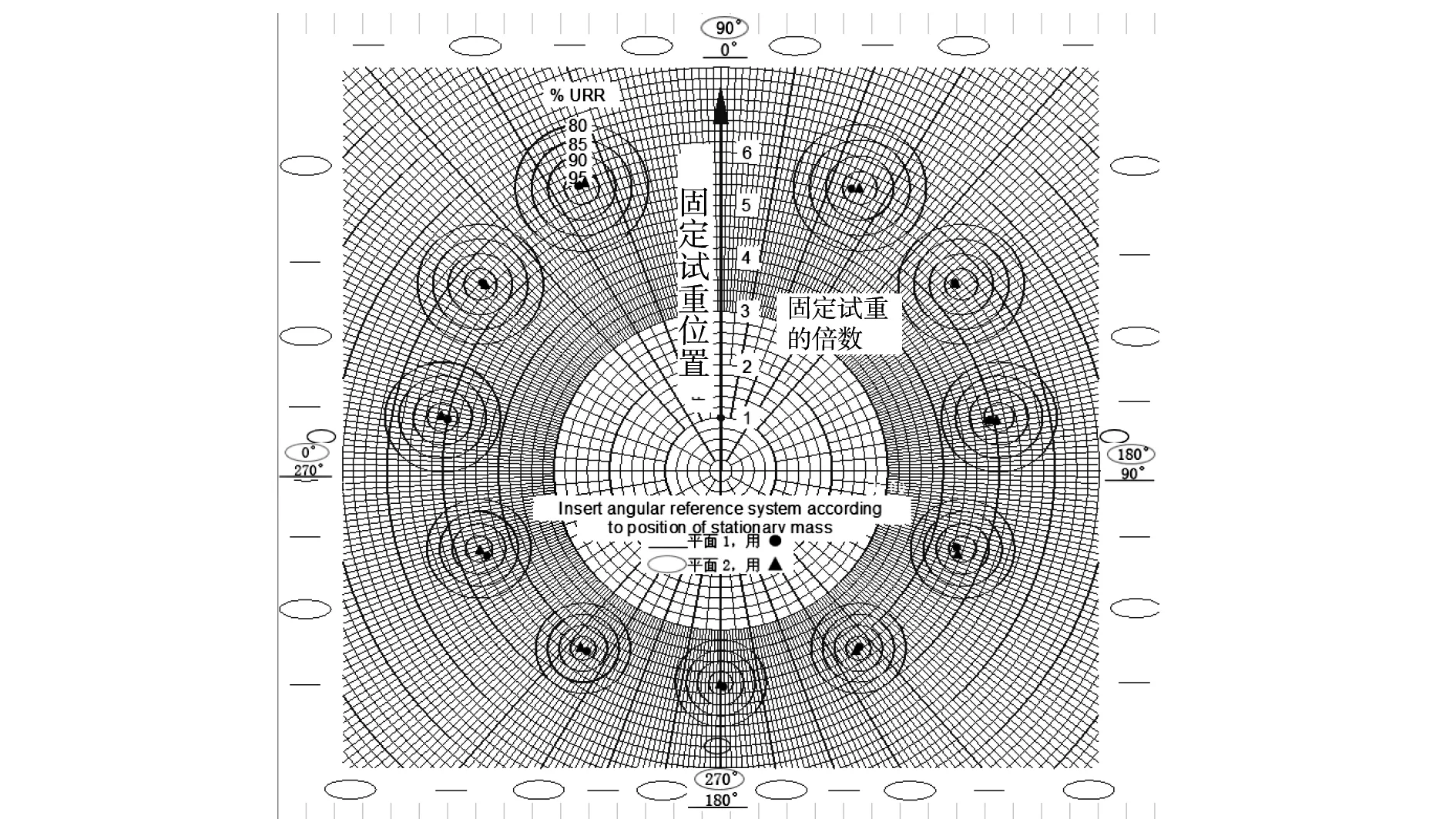
图4 双面试验用URR评定图

2.3.3 URR的评定

参考图4，如果一个试验点落在了最里面的极限圆之内(或压线)，表明该测量值达到了95%URR；若一个试验点落在95%的极限圆和90%的极限圆之间(或压线)，表明该测量值达到了90%URR，以此类推。

标绘在URR评定图上的所有试验点均应落在对应着标称的URR限值的极限圆内，允许每个校正平面有一点超出，则URR检测合格。

在本实例中，所有点都在95%的极限圆内，URR达到了标称的95%。

3 Umar、URR及评定的物理意义

在上述检测实例中，平衡机通过了Umar、URR检测，但是Umar、URR的物理意义及其评定的物理意义并不明晰。

3.1 Umar测量值的物理意义

Umar检测得到的测量值Ui(黑体表示矢量)并不是一个独立的不平衡量，而是3个不平衡量的矢量和。如图5所示，以试验平面1为例分析3个矢量。

(1)校验转子的剩余不平衡量Ua，其为试验准备完成后校验转子的剩余不平衡量，是大小和角度固定的系统量，一般要小于0.5Umar。表1中“第四次运行”记录的不平衡量即为Ua。

(2)在平面3上加装试验质量m10后产生的不平衡量，其在平面1产生的不平衡量Ub为5Umar，方向为试验质量m10加装的角度，是一个大小不变但角度变化的系统不平衡量，图5所示为m10加装在30°位置，图中的实线圆半径为5Umar，两个虚线圆半径分别为0.88×5Umar和1.12×5Umar。

(3)在给定的测量条件下，平衡机的随机测量误差Uc是一个大小和角度随机变化的不平衡量。另外，校验转子上加装试验质量的平面3外圆半径误差及轴向位置误差会影响测量值，本文把这种影响归到随机测量误差Uc中。

按如上分析，有：

Ui=Ua+Ub+Uc

(1)

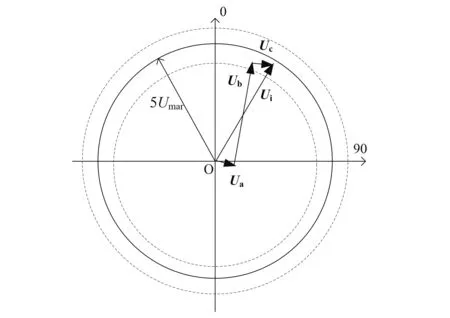
图5 Ui测量值示意图

3.2 Umar评定的物理意义

对Umar评定的本意是考核所有12个测量值Ui的大小在理论值5Umar的±12%的范围内，即：

0.88×5Umar≤Ui≤1.12×5Umar

亦即：

4.4Umar≤Ui≤5.6Umar

由于不平衡量Ub的大小是恒定的5Umar，将公式(1)代入上面的不等式中，并减去Ub=5Umar，则有：

-0.6Umar≤Ua+Uc≤0.6Umar

0.6Umar实际上是1.2倍的Umar per plane；由于不平衡量没有负值，上式中出现的负值只是表征不平衡量的方向是反向的，如只考虑不平衡量的大小，则有：

Ua+Uc≤0.6Umar

(2)

对应到每面最小可达剩余不平衡量，则有：

Ua+Uc≤1.2Umar per plane

因此，Umar评定的物理意义为：校验转子每个试验平面剩余不平衡量Ua与随机误差不平衡量Uc的矢量和的量值，在每一检测点小于0.6Umar(或小于1.2Umar per plane)。校验转子总的剩余不平衡量是一个平面的两倍，即公式(2)的两倍，亦即有：每一个检测点，校验转子剩余不平衡量与随机误差不平衡量的矢量和的量值小于1.2Umar。

需要注意的是，国家标准[1]对Umar的评定，不是对测量值Ui的绝对大小进行评定，而是对每一个测量值大小除以12个测量值的平均值后的“倍数”进行评定，倍数在范围0.88～1.12之内为检测通过。

3.3 URR测量值的物理意义

URR检测过程中，测量值Uj是4个不平衡量的矢量和。如图6所示，以试验平面1为例进行分析。

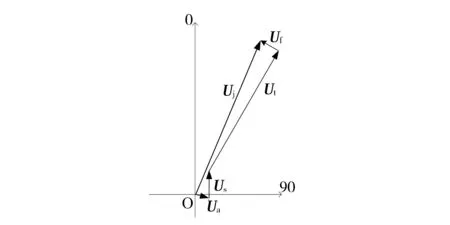
图6 URR测量值物理意义示意图

(1)校验转子的剩余不平衡量Ua。本检测实例是在检测完Umar后接着进行URR检测，此处Ua即为Umar试验准备后转子的剩余不平衡量。

(2)加装在试验平面1上的固定试验质量m30产生的不平衡量Us。该不平衡矢量的大小等于30Umar，角度为固定试验质量加装的角度0°，是一个大小和方向固定的系统不平衡量。

(3)加装在平面1上的移动试验质量m150产生的不平衡量Ut。该不平衡量的大小等于150Umar，其角度为m150加装的角度。Ut是一个大小不变但方向变化的系统不平衡量。图6所示为m150加装在30°位置时产生的不平衡量。

(4)在给定的测量条件下，平衡机的随机测量误差Uf，其大小和方向是随机的。对Uf作如下说明：

(a)随机测量误差与校验转子在测量平面上的不平衡量大小有一定的关系，不平衡量越大，随机误差一般越大。做URR检测时，平面1和平面2都有不平衡量，且在不同的检测点不平衡量的大小不同。在本检测实例中，其范围在120Umar到176.7Umar之间。

(b)平衡机在进行两个平面测量时，其中一个平面上的不平衡量会对另外一个平面产生一定的影响，这种影响也称为平面分离影响。本文把该影响归到随机误差Uf中。

(c)校验转子上加装试验质量时，半径上的误差、角度误差、轴向的位置误差、试验质量误差和质心误差，也会产生不平衡量误差。本文把该类影响归到随机误差Uf中。

按如上分析有：

Uj=Ua+Us+Ut+Uf

(3)

3.4 URR的物理意义、URR评定的物理意义

3.4.1 URR物理意义

URR的定义为“经过一次平衡校正减少的不平衡量与初始不平衡量的比值”[3]，并且“此不平衡量减少率是应在假定增加和去除质量无误差，操作平衡机具有正常技能并细心的情况下给出”[1]。从上面的定义，并参考图6，可做出如下归纳：

(1)不平衡量的校正假定没有误差，则通过一次校正，测量值Uj被100%校正掉。因此，经过一次平衡校正减少的不平衡量，就是测量值Uj。

(2)初始不平衡量为Ua、Us、Ut的矢量和。由于Ua的量值较小，国家标准[1]建议小于0.5Umar，且每次做测量准备后得到的值是不一样的，在考虑初始不平衡量时，先剔除Ua，则初始不平衡量为Us和Ut的矢量和，如图7所示。

UR=Us+Ut

此处的初始不平衡量UR实际上是测量值Uj所对应的理论不平衡量。

(3)按URR的定义及上述分析，URR的物理意义实际为测量值Uj与其对应的理论不平衡量UR的比值，即:

URR=Uj/UR

(4)

考虑到Uj、UR都为矢量，URR的物理意义可表述为：URR为测量值与理论不平衡量的接近程度，或是相对测量准确度，以百分比表示。如URR为95%，表示测量值与对应的理论值的接近程度为95%，相对测量准确度为95%。

公式(4)中，Uj、UR都是矢量，且两个矢量起点相同，不能直接对比大小，因此需要进行转化。

参考图8，把理论不平衡量UR与测量值Uj的矢量差记为Ur，则有：

Ur=UR-Uj

(5)

Ur实示上是测量误差，大小等于上述随机误差Uf，但方向相反。Ur也是理论不平衡量UR经一次平衡校正掉Uj后的剩余不平衡量。

公式(5)可转化为：

Uj=UR-Ur

则URR可表示如下：

URR=Uj/UR=(UR-Ur)/UR= 1-Ur/UR

(6)

上式中的Ur、UR虽然都是矢量，但因起点不同，可以只进行大小量值(Ur和UR)的比较，即可用以标量进行比较：

URR=1-Ur/UR

(7)

Ur/UR比值的物理意义实际上是相对测量误差，因此URR的物理意义也可表述为：用100%减去相对测量误差(%)后的百分数，比如，URR是95%，则对应相对测量误差是5%。

3.4.2 初始不平衡量UR的计算方法

参考图7，Us为固定试验质量产生的不平衡量(图中O1是Us的矢量端点)，Ut为移动试验质量产生的不平衡量，初始不平衡量UR的大小和角度按如下公式计算：

(8)

(9)

式中，α为移动试验质量与固定试验质量加装方向间的夹角，即移动试验质量所加的角度；γ为初始不平衡量UR与固定试验质量加装方向之间的夹角，即UR的角度。

图7 初始不平衡量UR

3.4.3 URR评定的物理意义

对URR的评定，是通过11组同心的极限圆进行。11组同心极限圆的圆心是初始不平衡量UR矢量的端点(图7和图8中的圆心O2)。当移动试验质量分别加装在11个不同角度时，形成11个不同的极限圆圆心，圆心位置按公式(8)、公式(9)计算。

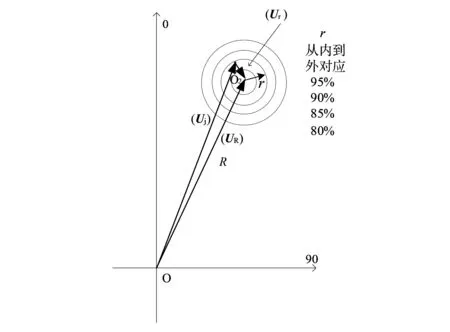
图8 URR评定的极限圆

将公式(7)变换为如下表示形式，极限圆的半径为下式中的Ur。

Ur=UR(1-URR)

(10)

国家标准[1]中给出了URR取值为95%、90%、85%、80%时极限圆半径Ur，其分别为5%UR、10%UR、15%UR、20%UR。

国家标准[1]中对于极限圆半径量值Ur的计算，还考虑了校验转子剩余不平衡量Ua的影响。在双面检测时，在上述Ur的基础上每面另加了0.5Umar，即有：

(11)

另外，国家标准[1]中对于URR的评定不是按不平衡量的绝对量进行评定，而是将不平衡量Uj、UR和Ur除以固定试验质量产生的不平衡量值Us后的一个倍数进行评定。极限圆圆心离坐标原点的倍数R, 也是一个矢量，由下式计算得到：

(12)

极限圆半径倍数r由式(11)除以Us得到[1]：

(13)

按公式(12)、(13)，并基于固定试验质量为30Umar，得表4(倍数表)，即国家标准中的表B.1[1]。表4中列出了达到标称URR的95%、90%、85%、80%时，在6个测量点对应的极限圆圆心R坐标(倍数和角度)和极限圆半径r倍数。另外5个测量点的极限圆圆心和半径倍数与表4中的前5个点的数据为对称关系参考前面图4。

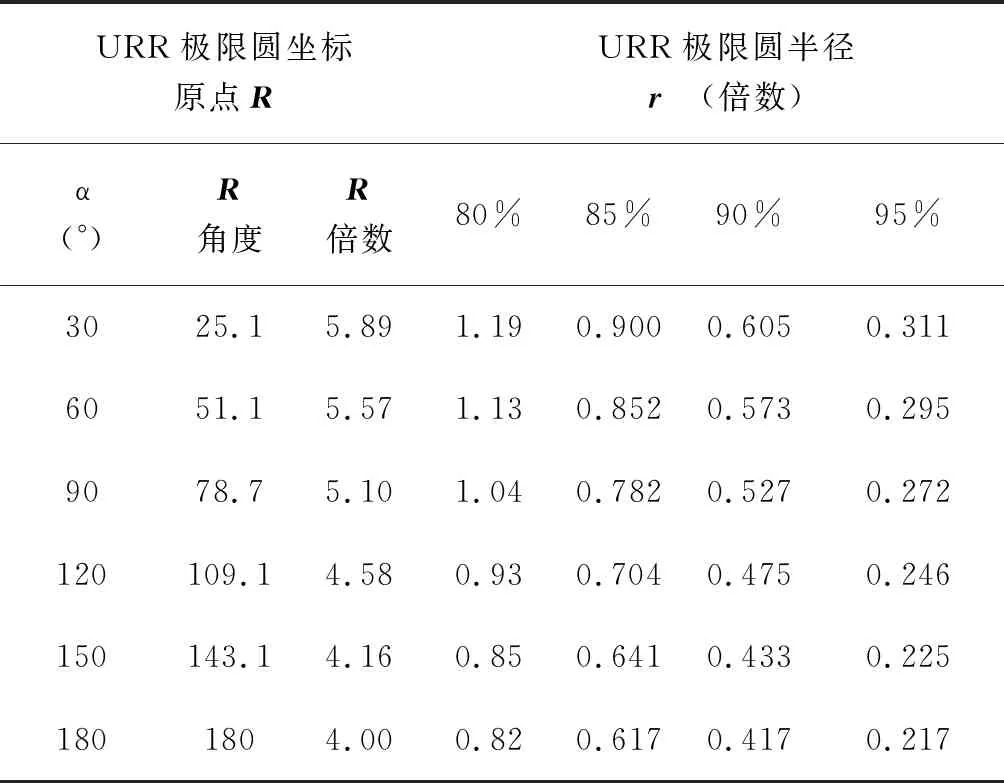
表4 双面试验URR极限圆数据(倍数表)

按前述对URR的评定及分析，可知国家标准[1]中URR评定的物理意义为：在每一个测量点，测量值与初始不平衡量的接近程度达到标称的URR百分比 (每面允许一点超出)。

4 Umar、URR存在的问题

(1)Umar和URR的名称含糊，定义不准确，且名称和定义与其物理意义不相符。

Umar的名称为“最小可达剩余不平衡量”，定义为“平衡机能使转子达到的剩余不平衡量的最小值”，但实际物理意义为：校验转子的剩余不平衡量与随机误差不平衡量的矢量和的量值，在每一个检测点小于1.2Umar。做两面检测时，每个试验平面的剩余不平衡量与随机误差不平衡量的矢量和的量值，在每一检测点小于0.6Umar，或小于1.2Umar per plane。Umar指标所考核的，既不是单纯平衡机的精度，也不单纯是校验转子剩余不平衡量，而是两者的组合。

URR的名称为“不平衡量减少率”，其定义为“经过一次平衡校正减少的不平衡量与初始不平衡量的比值”，实际物理意义为测量值与对应理论值的接近程度(以百分比表示)。URR与不平衡量校正没有任何关系，不平衡量减少率只是一个结果，并不是其本质的物理意义。

(2)用Umar、URR对平衡机进行检测，只是定性地判定是否达到平衡机标称的指标。即使通过上面的详细解析，清楚地知道Umar、URR的检测过程、物理意义及评定的物理意义，并且检测合格，仍然给不出校验转子的不平衡量的准确值，也给不出平衡机的测量精度的准确值。用同一个校验转子及同样的试验质量对两台机器进行检测，两台机器都通过了Umar和URR检测。再用两台机器分别检测该校验转子的不平衡量，得出不同的测量值，无法验证哪台平衡机是准确的。用现有的国家标准[1], 无法进行平衡机之间的比对。

(3)Umar、URR的检测，分别检测了12个点和11个点，检测过程复杂，对应的校验转子做得也非常复杂。但实际上，测量值Ui、Uj中所包含的不平衡量，除了转子的剩余量及随机误差外，其它通过施加试验质量产生的不平衡量是确定的，检测12个点和11个点并没有给出比检测1个点更多的信息。也就是说，通过检测1点获得转子的剩余不平衡量(Ua)及随机测量误差 (Uc或Uf)，可以基于10Umar、50Umar、150Umar所产生的不平衡量计算出其它点的测量值的公称值及变化范围。对于归类于随机误差Uf中的平面相互影响，如有必要，可单独考核。实际上，随着动平衡测量技术的发展，平面影响越来越小，已不是影响平衡机精度的主要因素。

(4)平衡机通过了Umar检测，则认为该平衡机“已经达到标称的最小可达剩余不平衡量Umar”[1]，亦即认为“平衡机能使转子达到剩余不平衡量的最小值”[3]。这种定义容易将平衡机的生产者和用户引入误区，即认为通过Umar检测的平衡机，平衡机的测量精度就能小于Umar，或校验转子的不平衡量就小于Umar。 对于卧式通用平衡机，现在很多生产厂家给出的标称最小可达剩余不平衡度emar达到0.1g·mm/kg，对应5kg的校验转子，Umar=0.5g·mm，每面Umar per plane=0.25g·mm。但需要特别指出的是，此处Umar值，是按国家标准[1]检测平衡机时的特定条件，即在平衡机摆架位置、支撑及限位等处于一个特定固定的状态，校验转子与支撑、限位件等保持特定固定的关系，且没有上下取放校验转子的条件下获得的。这些特定固定条件一经改变，用同一台平衡机再测量该校验转子的剩余不平衡量，一般是Umar的数倍。因此，按国家标准[1]进行Umar检测所达到的转子的剩余不平衡量并没有再现性。

另外，国家标准[1]对Umar的评定，不是对测量值Ui绝对大小进行评定，而是对每一个测量值Ui除以12个读数的平均值后的“倍数”进行评定。这种考核倍数的方法，不能检测平衡机的“尺度”是否正确。换言之，通过了Umar检测的平衡机，其尺度可能是错误的。

(5)Umar、URR的检测，是用国家标准[1]规定的校验转子对平衡机进行检测。在实际工业生产中，很多用在生产线上的专用平衡机，由于其结构的限制，无法支撑或是驱动校验转子，国家标准[1]无法对这些专用平衡机进行检测。

(6)国际标准[2]第一版是1975年发布的。45年前，计算机还没有作为工程人员的一般工具来使用，对矢量进行计算是因难的。平衡机的测量系统是指针式的或是瓦特表式的，电测系统全部是模拟电路。标准中对URR的评定还在“使用市售的或自制的极坐标图纸”[1]，用极坐标图纸做图涂点评定。这种方法既不准确，也耗费时间。这种做法是由40多年前计算水平决定的。现在已经是21世纪，对于矢量加减计算，可以在计算机上容易完成，计算得到每一个检测点的Umar、URR准确值，没有必要用手工绘制图3和图5式的评定图。

(7)在进行Umar或是URR检测时，测量值并不一定是100%转子本身的不平衡量，而可能是转子的不平衡量与转子之外的不平衡量(如平衡机零点的偏倚、驱动装置的不平衡量及测量系统中可能带有的补偿量、立式机器主轴和夹具的不平衡量等)的矢量和。在没有检测及扣减转子之外的不平衡量的前提下，平衡机测量转子不平衡量的零点未知，即上面的图示坐标中的零点是被测量转子及平衡机整个系统的零点，并不一定是转子不平衡量测量的零点。

(8)在检测Umar或是URR时所加装的试验质量，其质心是假定在砝码的几何形心上。实际上，砝码材质并不一定是均质的，砝码的质心可能会偏离其几何形心。虽然这种偏离可能相对较小，从工程角度可以忽略，但从计量的角度，质心偏离几何形心的量值需要检测并得到其量值后，才能判断是否可以忽略不计，而不能在检测前就想当然地忽略掉。

5 结束语

基于如上的解析，对国家标准[1]中最小可达剩余不平衡量Umar和不平衡量减少率 URR两个指标给出如下评价：

(1)两个指标名称和定义不清，名称与其物理意义不相符。在平衡机检测实践中，常有用户要求解释Umar、URR的物理意义及评定的物理意义，但如本文所解析，解释清楚这两个指标的物理意义和评定的物理意义并不容易。

(2)两个指标的检测所需要的校验转子结构复杂，检测过程繁琐，但这种复杂和繁琐并不是必要的。

(3)检测方法和结果只是定性的评定，检测结果不能比对，不能传递，也没有溯源到基本物理量。

(4)由于国家标准[1]及之前版本的先天不足，在现实的平衡机检测实践中，对于Umar、URR的检测，一般只是生产厂家在平衡机出厂时检测，在实际使用中，很少有平衡机用户使用。我国在各行各业有相当体量的平衡机在使用，进行定期检测的平衡机只占相当少的比例，大部分平衡机长年处于未被检测的状态。出现这种情况，很大程度上是因为平衡机检测标准制定的不当。

(5)国家标准[1]对应的国际标准第一版发布于1975年，基于当时的平衡机技术水平、科技水平及对不平衡量检测的认知水平，推出Umar、URR两个检测指标，取代了之前各个国家采用的不同的平衡机检测指标，具有积极意义。但40多年来，标准没有与时俱进，顺应科学技术的发展。

(6)转子的不平衡量是转子物理性能的客观存在。转子的不平衡量是可测量、可溯源的。笔者将另篇介绍可溯源的转子不平衡量检测方法和平衡机精度检测方法。