基于子结构实验的橡胶减振器动态特性预测研究

刘德宇，郭勤涛，陶言和，王秀刚

(南京航空航天大学机电学院，江苏 南京 210016)

橡胶减振器具有形状自由度大、减振性能良好、成本相对低廉等优势，被广泛应用于轨道列车的减振系统中，连接地板与车体的橡胶减振块对列车的运行平稳性与乘员的舒适性起着重要作用。橡胶是一种典型的超弹性材料，硫化体系复杂，并且硫化过程中温度、压力和时间对制品质量影响较大[1-2]。在材料和加工工艺相近的情况下，橡胶结构的刚度和阻尼存在较大的不确定性，因此对减振系统中橡胶减振元件的不确定性进行量化，有利于提高仿真计算的准确性。黄建龙等[3]使用Mooney-Rivlin模型对橡胶材料进行仿真分析，介绍了获取模型材料参数的实验方法。刘萌等[4]仅使用单轴拉伸实验识别模型参数，证明了在某些工况下简化材料实验种类的可行性。潘孝勇[5]介绍了橡胶材料动态特性实验的方法，总结了橡胶元件动态特性参数的确定公式。郭勤涛等[6]对有限元模型确认方法进行了研究，介绍了模型确认的总体思路与实现方法。

本文选用Mooney-Rivlin超弹性模型表征橡胶材料的弹性特性，用频域黏弹性模型表征橡胶材料的频变特性，对材料进行单轴拉伸实验与简单剪切实验，通过公式计算与拟合应力-应变关系曲线获取模型参数，并对模型参数及其仿真响应进行不确定性量化分析。

1 橡胶材料的本构模型

1.1 橡胶材料的超弹性理论模型

橡胶是一种超弹性材料，常使用应变能密度函数表征其力学特性。实际应用中常使用Mooney-Rivlin模型描述橡胶的应变能密度函数，该模型基于唯象理论，使用张量不变量作为应变能密度函数的自变量，在小应变范围内拟合效果良好，同时模型方程简单，参数获取方便，因此被广泛应用于橡胶件的工程分析中。二参数Mooney-Rivlin模型应变能密度函数为：

W=C10(I1-3)+C01(I2-3)

(1)

式中：W为应变能密度；C10与C01均为Rivlin系数；Ii(i=1,2,3)为第i阶Green应变不变量。

橡胶材料的不同应力-应变状态可由单轴拉伸、单轴压缩以及纯剪切实验表示，考虑到实际实验过程中的难易程度与精度，常用等双轴拉伸与平面拉伸实验代替单轴压缩与纯剪切实验。由于橡胶材料的不可压缩性，可以认为I3=λ1λ2λ3=1，其中λj(j=1,2,3)为3个方向的主伸长率。不同变形状态时的工程应力σ与对应的主伸长率的关系为[7]：

单轴拉伸

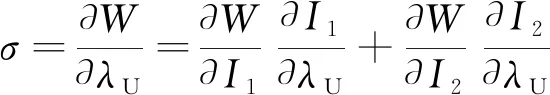
(2)

等双轴

(3)

平面剪切

(4)

式中：λU,λB,λP分别为不同变形状态下的主伸长率。

变形张量不变量与实验中主伸长率的关系为[7]：

单轴拉伸

(5)

等双轴

(6)

平面剪切

(7)

将式(1)和式(5)(式(6)、(7))代入式(2)(式(3)、(4))，便可计算得到材料在不同变形状态时的工程应力。考虑到橡胶结构件的实际工况及实验室条件，本文仅使用单轴拉伸实验识别橡胶材料参数。

1.2 橡胶材料的频域黏弹性理论模型

橡胶隔振器的动态特性与激振频率的高低及振幅大小有关，小振幅工况下可以忽略振幅变化对橡胶动态特性的影响，只考虑由橡胶材料黏弹性确定的频率相关性。本文使用频域黏弹性模型表征橡胶材料的频变特性。

对橡胶材料进行动态简单剪切实验时，试件受到的谐波剪切应变激励κ(t)为[8]：

κ(t)=κ0eiωt

(8)

τ(t)=G*(ω)κ0eiωt=[Gs(ω)+

iG1(ω)]κ0eiωt

(9)

式中：Gs(ω),G1(ω)分别为剪切模量G*(ω)的实部和虚部，定义为剪切存储模量和剪切损失模量[5]。

剪切松弛函数g(t)定义为[8]：

(10)

式中：GR(t)为与时间相关的剪切松弛模量；G∞为准静态剪切模量，可通过试样的静力加载实验分析获得。

Gs(ω)和G1(ω)可表示为：

Gs(ω)=G∞[1-ωIm(g*)]

(11)

G1(ω)=G∞ωRe(g*)

(12)

式中：g*为g*(ω)的简写，g*(ω)为g(t)的傅里叶变换；Re(g*)和Im(g*)分别为g*(ω)的实部和虚部。

剪切应力的幅值|τ|和相位角δ可分别表示为：

(13)

(14)

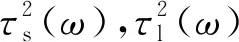
1.3 模型精度的确认准则

模型的精度与适用范围通过确认准则判断，考虑不确定性因素时，使用重合度准则判定不同响应分布的一致程度[6]：

J(P)=PDFtest∩PDF

(15)

式中：PDF和PDFtest分别为仿真计算和实验响应特征的概率密度分布；J(P)的值为两个响应概率密度分布的重合面积。该准则可以比较全面地判定仿真计算与实验结果是否保持一致，当两个结果的概率密度函数曲线完全重合时，J(P)的值为1，表示仿真的响应特征完全可以取代实验数据体现的结构特性。

2 本构模型的参数确定及量化

2.1 单轴拉伸实验及参数识别

根据1所述的本构模型参数获得方法，采用单轴拉伸实验[9]对橡胶材料进行应力-应变测试，选用标准GB/T 528—2009中的1A型哑铃状试样，应变水平选择与实际工况相近的0.5。单轴拉伸试样如图1所示。

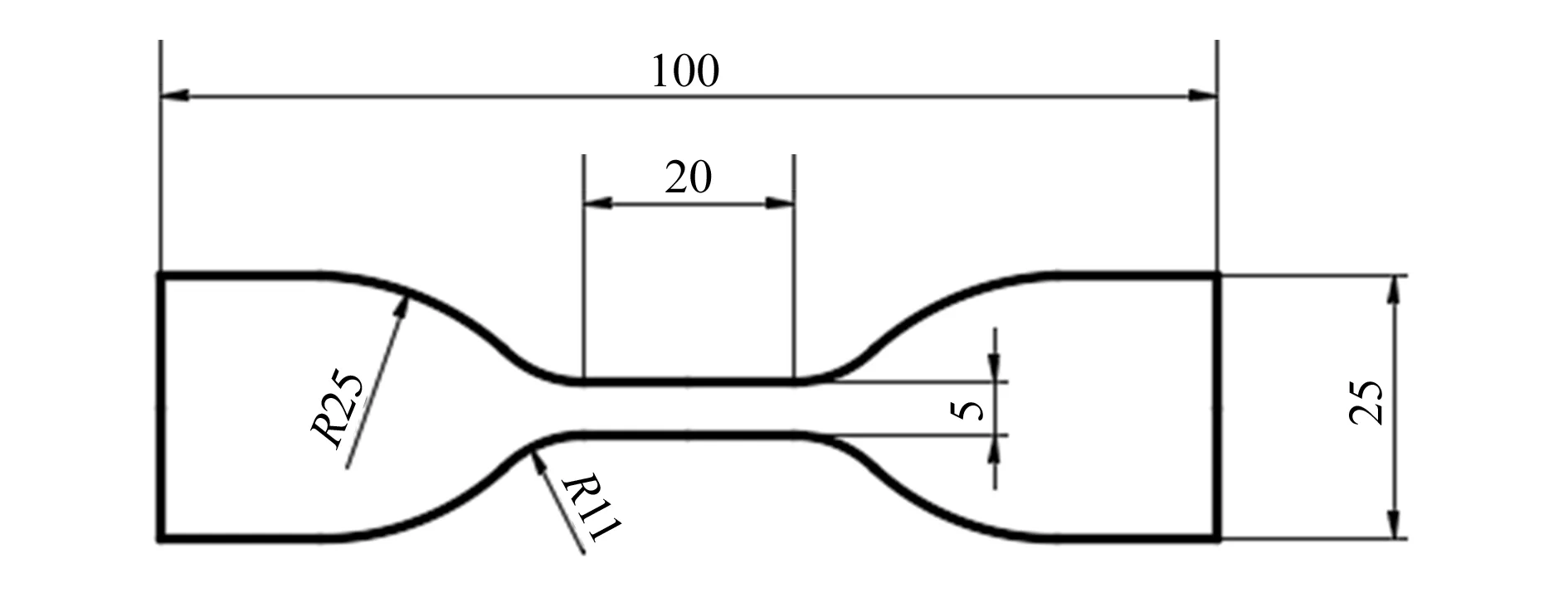
图1 单轴拉伸试样

橡胶材料的非线性特性使其在材料参数识别过程中存在较大的不确定性。概率论与数理统计技术为不确定性量化分析提供了统计及检验方法。实际工程中通常使用正态分布对随机变化的不确定性参数进行分布估计与检验，本文通过正态分布方法对橡胶参数进行不确定性量化分析。单轴拉伸实验过程中，为了量化材料本身差异与实验操作中所带来的不确定性，分别对11件试样进行了拉伸实验，考虑到Mullins效应的影响，正式拉伸实验前对试样循环加载5次，以消除Mullins效应。将试样对称地夹在拉力实验机的上下夹持器上，使拉力均匀地分布在试样的横截面上。启动拉力实验机，在整个实验过程中连续监测试样长度和受力变化，如果试样在其狭窄部位以外的地方断裂则舍弃该实验结果，并另取试样重新进行实验。实验获得的11件试样的应力-应变关系如图2所示，使用最小二乘法拟合关系曲线可获得模型参数C10和C01。

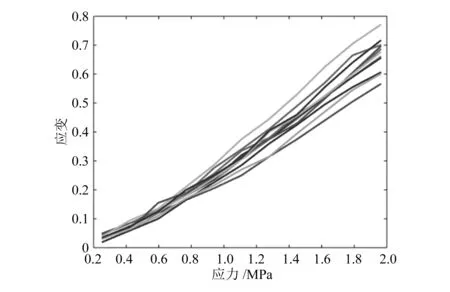
图2 单轴拉伸应力-应变关系

对单轴拉伸实验所获得的参数进行正太分布拟合，得到Mooney-Rivlin本构模型参数C10服从N(0.589 8,0.042 72)，C01服从N(0.258 2,0.061 32)。

2.2 简单剪切实验及参数识别

通过动态简单剪切实验获得橡胶材料的频域黏弹性材料模型参数，简单剪切试样及实验台如图3所示，该实验台可以测量不同频率下激振力与剪切变形的大小。

降低激振频率进行准静态简单剪切实验，由准静态简单剪切实验可测得剪切力Fs0与试样位移xs0，从而得到剪切应力τs0为：

(16)

式中：2A为橡胶试件的剪切面积。

剪切应变κs0为：

图3 简单剪切实验台

(17)

式中：t0为橡胶试件的厚度。

准静态剪切模量G∞为：

(18)

式中：Δτs0,Δκs0为准静态剪切应力与准静态剪切应变。

由动态简单剪切实验可以测得试样随频率变化的存储刚度Ks、损失刚度Kl和阻尼角，存储力Fs(ω)和损失力Fl(ω)分别为：

Fs(ω)=Ks(ω)x0(ω)

(19)

Fl(ω)=Kl(ω)x0(ω)

(20)

式中：x0(ω)为不同频率下的响应位移振幅。

与存储力Fs(ω)和损失力Fl(ω)对应的剪切应力τs(ω)和τl(ω)分别为：

(21)

(22)

剪切应变κ(ω)为：

(23)

剪切存储模量Gs(ω)和剪切损失模量Gl(ω)为：

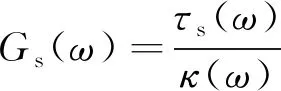
(24)

(25)

表示橡胶材料黏弹性的参数ωRe(g*)和ωIm(g*)分别为：

(26)

(27)

用以上计算公式处理实验数据，得到剪切试样的ωRe(g*)和ωIm(g*)随激振频率变化的曲线，如图4所示。从图中可以看出，|ωRe(g*)|和|ωIm(g*)|随激振频率的增加而增加，并且|ωIm(g*)|的增幅更明显。

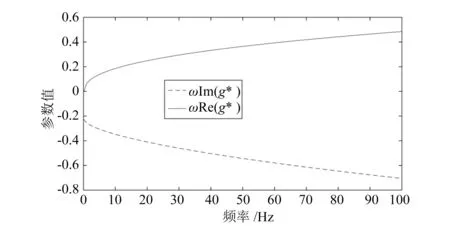
图4 ωRe(g*)和ωIm(g*)频变曲线

对激振频率为20 Hz时的6组橡胶试样进行动态剪切实验，得到该频率下的黏弹性参数，对参数进行正态分布拟合，得到ωRe(g*)服从N(0.204 2,0.001 42)，ωIm(g*)服从N(-0.385 8,0.000 392)。

3 橡胶减振系统的响应预测

3.1 减振系统的响应验证

某橡胶减振系统的有限元模型如图5所示，含有7 128个六面体单元，橡胶单元材料属性为超弹性与黏弹性叠加，约束面为橡胶块底面，加载处为钢板中心位置，在加载点施加扫频集中力。虽然橡胶元件尺寸及形状与实际工程中列车的减振块不同，但为减振块的分析提供了方法。使用激振器、力传感器及加速度传感器搭建动力扫频实验台，实验中在加载点施加扫频集中力，测量加载力信号与钢板加速度信号，对信号进行频域变换后与模型的仿真计算结果进行比较，如图6所示。

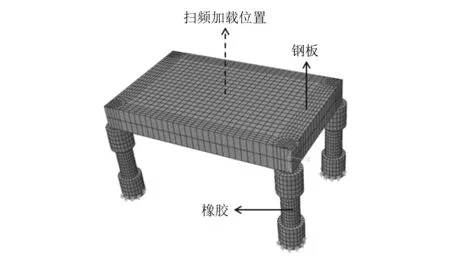
图5 减振系统有限元模型

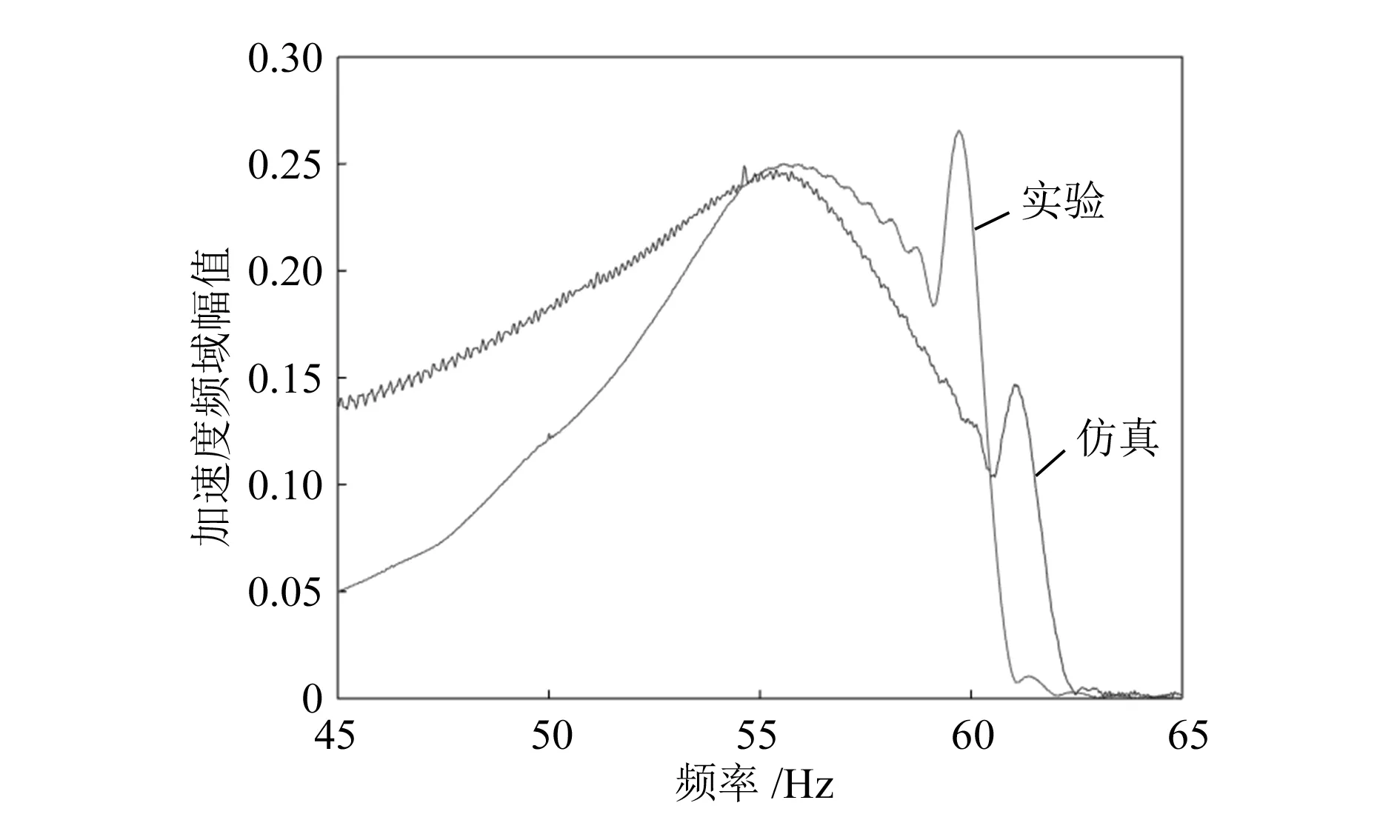
图6 频响曲线对比

为了对减振系统模型的响应进行预测，在激振频率为20 Hz时进行多组实验，记录钢板加速度信号。对实验值进行拟合，实验得到的加速度响应服从Ae～N(0.269 3,0.028 22)。

3.2 基于重合度准则的量化

对减振系统模型进行20 Hz激励下的响应计算，使用蒙特卡罗法随机抽取材料黏弹性参数，计算20组加载后的减振系统模型加速度响应，对结果进行正态分布拟合，模型响应峰值服从As～N(0.256 2,0.002 12)。

模型预测响应峰值概率密度分布与3.1节实验测得加速度峰值分布的比较结果如图7所示，超弹性-黏弹性模型与实验值的重合度为76.08%。根据重合度准则，可判断使用超弹性-黏弹性模型对减振系统响应预测进行的量化是合理的。

图7 预测与实验的概率密度分布

4 结束语

本文对橡胶减振器试样进行了实验，识别其超弹性模型与黏弹性模型材料参数，验证了小振幅激励下橡胶元件超弹性-黏弹性叠加模型的有效性。将模型确认技术引入非线性材料的建模中，考虑材料参数识别过程的不确定性因素，验证了重合度准则的有效性，得到了具有一定置信度的减振器模型。所涉及的理论与方法具有深入研究的必要，对后续研究工作的建议如下：1)超弹性模型参数识别可增加等双轴拉伸实验与平面拉伸实验，提高所得参数的精度；2)橡胶材料建模忽略了材料的幅变特性，所得模型不适用于大变形工况，若需研究橡胶材料的幅变特性，有必要在本模型基础上增加弹塑性模型；3)本文所有实验均在室温进行，未考虑橡胶材料的温变特性，后续的相关研究可考虑这一因素的影响。