基于有限元的废金属破碎机关键件疲劳寿命分析

李伟毅,叶文华,李佳璇,江 腾,黄艰生,符 杰

(1.南京航空航天大学机电学院，江苏 南京 210016)

(2.江苏华宏科技股份有限公司，江苏 江阴 214423)

废金属回收是缓解金属资源危机、实现节能减排的重要手段。废金属的自动化破碎与分选处理是废金属回收处理的一种先进方法，其核心设备是废金属破碎机，但国内学者在破碎机研制过程中，较少对关键部件疲劳寿命进行预测分析。破碎机在实际生产过程中易发生关键件疲劳损坏，从而引起生产事故，或在未达到疲劳寿命时就更换关键件，增加经济成本。因此通过技术手段模拟破碎机关键部件疲劳寿命，可以在很大程度上降低研发成本，缩短研发周期，提高破碎机的使用效率[1]。

对废金属破碎机而言，其本身具有大尺寸、大功率等特点，且多为单件生产，成本高昂，用物理样机实验的方式来获取关键部件疲劳寿命难度较大。随着计算机模拟仿真技术的进一步发展，可以借助有限元分析技术获取虚拟样机的疲劳寿命，将其与实际生产中破碎机关键部件的疲劳寿命对比，以改进虚拟样机模型，并形成通用的破碎机疲劳寿命预测模型，从而缩短产品研发周期。

郭红等[2]基于CATIA软件对单齿辊破碎机主要部件进行了有限元分析，分析了破碎机工作状态时的应力，但没有对其疲劳寿命进行分析。陈方述等[3]基于ANSYS软件对单辊破碎机锤头的疲劳特性进行了理论研究，但未与破碎机实际工作寿命进行对比。江腾[4]基于有限元软件分析了废金属破碎机的疲劳寿命，但是仅分析了一种工况下的理论疲劳寿命，未考虑复杂工况及实际生产中的安全系数。

目前，常用的累计损伤理论有线性累积损伤理论、双线性累积损伤理论和非线性疲劳累积损伤理论[5]。其中，线性累积损伤理论简化了疲劳机理，计算方便，但用该理论计算疲劳寿命，其结果与实际疲劳寿命相差较大；双线性累积损伤理论符合损伤在不同阶段发展的规律，但不能准确表达实际的损伤过程；非线性疲劳累计损伤理论以科尔顿-多兰公式为典型代表，考虑了多级复杂应力作用对疲劳寿命的影响，但公式相对复杂[6]。本文以科尔顿-多兰公式为基础，利用ANSYS/LS-DYNA软件建立废金属破碎机的虚拟样机并仿真。基于仿真结果，利用统计学方法对破碎机疲劳寿命进行预测分析，并与实际生产过程中关键部件的疲劳损坏时间对比，验证虚拟样机模型的正确性。

1 冲击破碎机理

对于大部分金属材料而言，当应力超过屈服极限时，会出现不可逆的塑性应变。在材料发生初始屈服后，当加载强度继续增加时，材料会产生进一步的塑性变形，此时由于强化现象，屈服条件改变，当应力达到新的屈服条件时，材料发生变形[7]。此时，材料的屈服条件不仅与塑性应变εijp及应力σij有关，还与金属的塑性变形过程有关。

为了得到复杂应力状态下金属的应力-应变关系，引入Prandtl-Reuse流动法则[8]：

(1)

式中：dλ≥0；λ为比例系数；εp为不可恢复的塑性应变[9]；F0为塑性势函数；σ为应力。式(1)表明任一点处的塑性应变增量只与该点处的应力σij有关。

在金属的弹性变形中，应力是由弹性应变引起的，因此有：

dσ=Dedεe=De(dε-dεp)

(2)

式中：De为弹性矩阵；εe为弹性应变；ε为总应变。

假设有一很小的增量载荷ΔP，且增量载荷的应力点满足屈服条件的表达式：

(3)

式中：K为体现塑性功能的参数。

将式(1)、式(2)代入式(3)，经过化简可得材料弹塑性应力-应变关系式：

dσ=Depdεe=(De-Dp)dε

(4)

式中：Dp为塑性矩阵；Dep为弹塑性矩阵。

由该冲击破碎机理可知，在废金属破碎机工作过程中，由于破碎过程具有较强的非线性特征，因此应使用非线性分析工具进行建模。

2 有限元模型建立及仿真结果

由于废金属破碎过程中涉及到复杂的非线性问题，因此采用在工程领域有较高认可度的ANSYS/LS-DYNA软件进行建模。

2.1 三维模型建立

本文以PSX-2250型大功率破碎机为例进行研究。由于破碎机整体结构具有零件多、装配关系复杂等特点，且部分部件对关键部件影响较小，如果基于完整的三维模型建立有限元模型，会在很大程度上增加建模的难度及计算时间，因此需要对原有三维模型进行简化。

简化后的整体结构如图1所示，仅保留主轴、锤轴、锤头、隔板等关键部件，只需简化倒角等对分析结果影响较小的区域，对隔套、端盖、轴承座等对整体结构强度影响较小的部件可简化为规则形状或取消，轴承部位可以用约束代替。简化后的破碎机主轴模型复杂度降低，大大减少了计算时间。

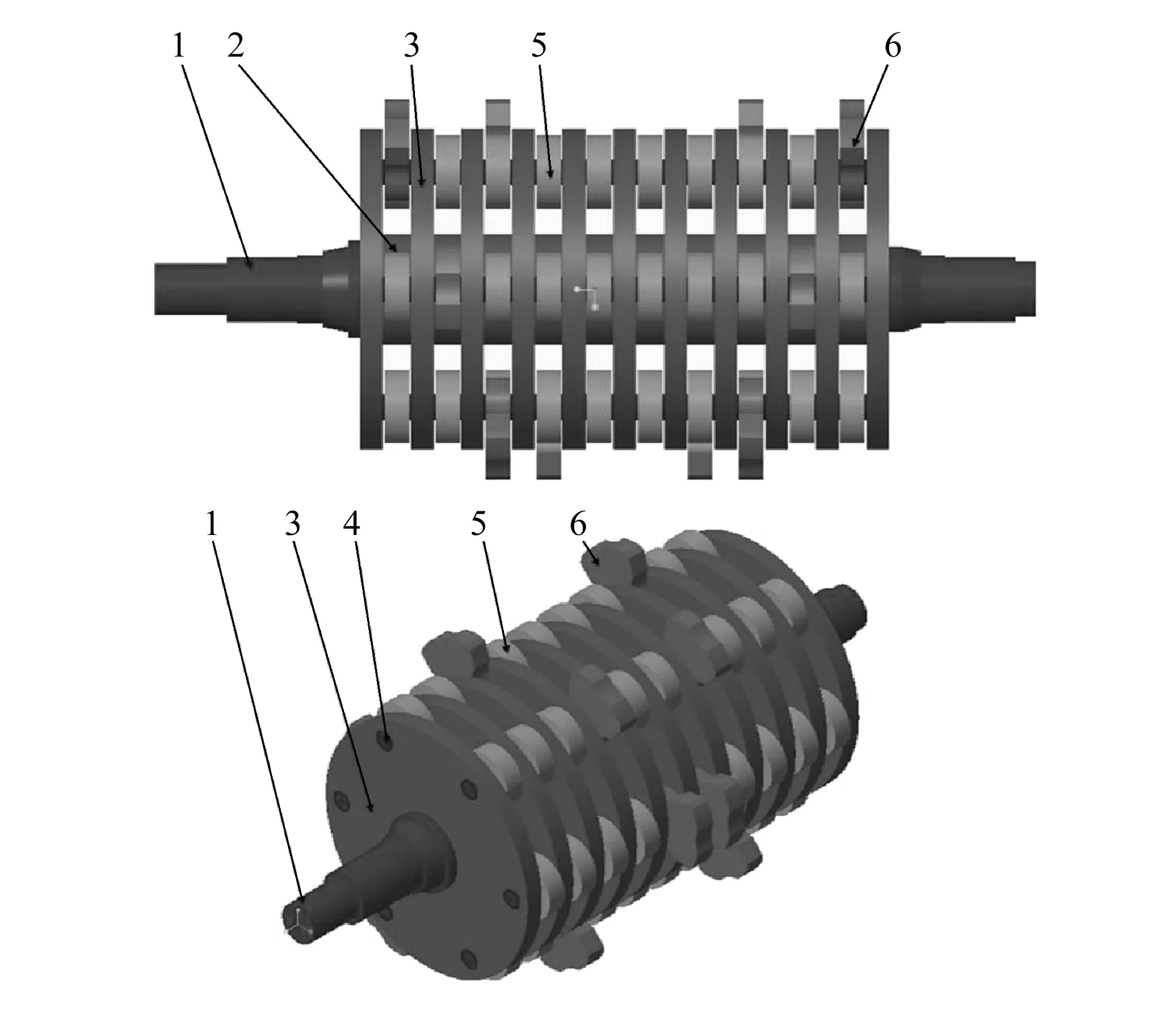
1—主轴；2—轴套；3—隔板；4—锤轴；5—隔套；6—锤头

在废金属破碎机工作过程中，被破碎物料种类十分复杂，模拟分析时很难以实际形状建模，因此需要对其进行简化。以废旧汽车为例，其车身各部件主要材料为钢材，外壳等部件均可视为钢板结构，因此可利用钢板等效替代被破碎物料建模。

2.2 材料及单元模型定义

由式(4)可知，在废金属破碎机实际工作过程中，被破碎物料具有较强的非线性特性，且会影响破碎过程，因此在仿真建模过程中，对被破碎物料进行材料选择时应选择随动塑性材料(plastic kinematic)模型，同时利用关键字*MAT_ADD_EROSION对其添加单元破坏依据，当某个单元应力应变达到破坏条件时，该单元出现失效。

破碎机各主要部件材料性能见表1。对于主轴辊等对破碎机寿命影响较小的部件，可采用刚体(rigid)模型，以提高计算效率。对于锤头等需要重点分析的部件，由于其采用高锰合金制造，具有较强的各向同性特征，因此在建模时可选用各向同性(isotropic)弹性材料。

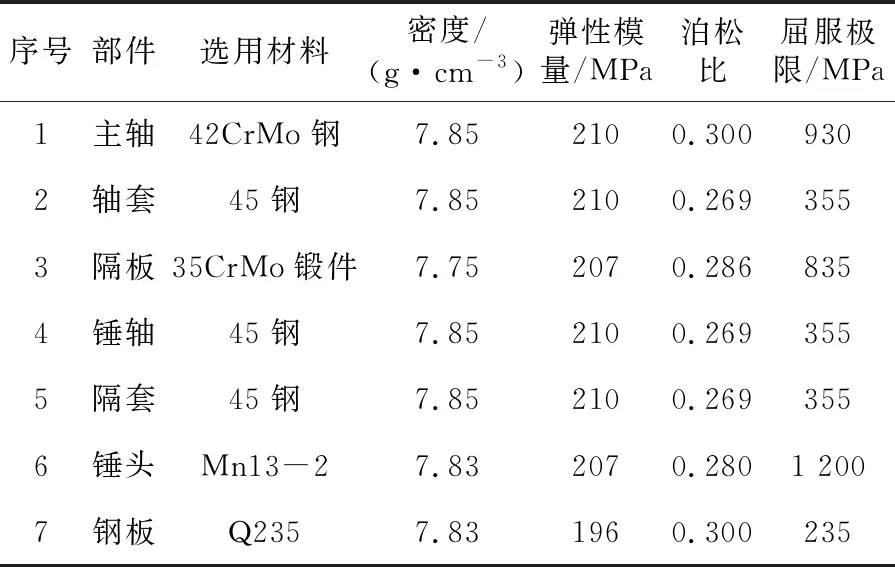
表1 破碎机各部件材料参数

由于破碎机工作过程中具有很强的非线性特征，且关键部件可能出现大变形甚至撕裂的情况，因此单元模型可采用3D Solid 164实体单元模型。该单元由8节点组成，支持所有许可的非线性特性，既能节省分析时间又能在大变形情况下增强可靠性。

2.3 网格划分

有限元分析中网格质量的好坏决定了计算结果的可靠性，因此在网格划分过程中应遵循以下规则：1)尽量保持结构的几何特征不变；2)过渡网格需要平缓，避免剧烈转变；3)对于实体结构尽量采用六面体单元。图2为划分网格后的破碎机模型。

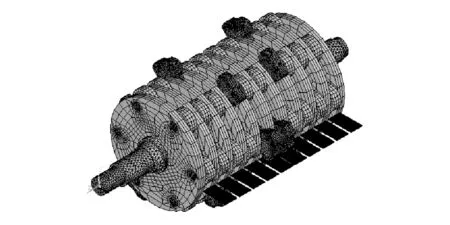
图2 划分网格后的破碎机模型

2.4 主要仿真参数设置

在破碎机建模过程中，需要定义破碎机不同部件之间的接触关系。在定义接触关系时，需要先生成各部件的Part。各部件Part号与表1中各部件序号一一对应。

其中主轴与隔板、隔板与锤轴之间认为是固联接触，可采用面面固联接触(TDSS)；锤轴与锤头、隔套与锤轴等之间的接触多为摩擦接触，可采用面面自动解除接触(ASTS)，并定义摩擦系数；钢板与锤头之间涉及破碎穿透等关系，因此需定义面面侵蚀接触(ESTS)；此外，由于钢板碎裂后会有部分碎片脱离钢板本身，可能出现同Part间的穿透现象，因此需定义侵蚀单面接触(ESS)。完整的接触关系定义见表2。

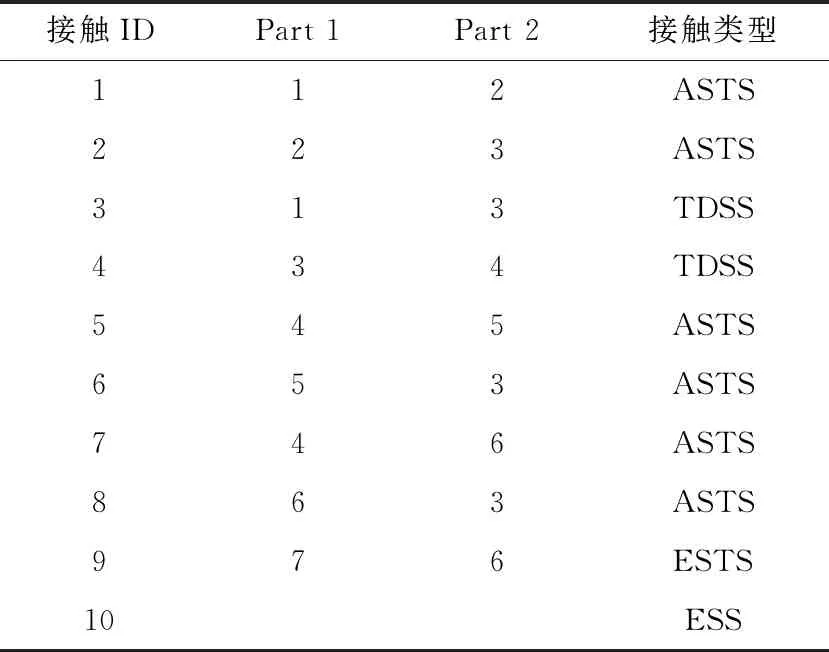
表2 接触关系设置

完成接触关系定义后，需对模型施加载荷。破碎机工作过程中由电机带动主轴转动，因此仿真时可将其等效为1个稳定的转速和1个绕轴向的扭矩。同时，由于破碎机结构较大，受重力影响较大，因此还需考虑重力的影响。针对金属破碎机的工作情况，对其施加载荷。

以下是对破碎机施加的载荷：

1)转速。电机实际工作转速为n=600 r/min，将其转换为角速度，即62.8 rad/s。

2)扭矩。在电机与主轴连接处施加扭矩T，T=9 550P/n=36(kN·m)，其中P=2 250 kW，为破碎机功率。

3)重力。利用关键字*LOAD BODY对其施加重力。

图3所示为破碎过程示意图，其中主轴绕Z轴转动，因此需限制其X，Y，Z方向的平动及绕X，Y轴的转动，锤头、钢板等部件同理设置约束关系。同时，在轴承部位添加约束，模拟轴承的转动约束及定位作用。

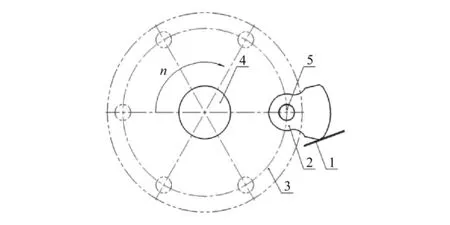
1—废钢板；2—锤头；3—隔板；4—主轴；5—锤轴

2.5 关键零件仿真结果

调用LS-DYNA的后处理器LS-PREPOST并查看求解结果，可以得到应力云图、接触力、能量等参数曲线。

通过破碎机关键零件应力云图(图4)可得主轴在工作过程中的最大应力为261 MPa，对应的应力循环次数超过107，低于主轴材料的疲劳极限，因此主轴在正常工作情况下不会发生疲劳损坏。锤头的应力主要集中在其与锤轴连接处以及锤头前端边缘，锤轴的应力集中在其与锤头连接部位。从仿真结果可以得到锤头和锤轴的危险部位的载荷-时间历程曲线，如图5、图6所示，可为疲劳寿命计算作准备。

图4 破碎机关键零件应力云图

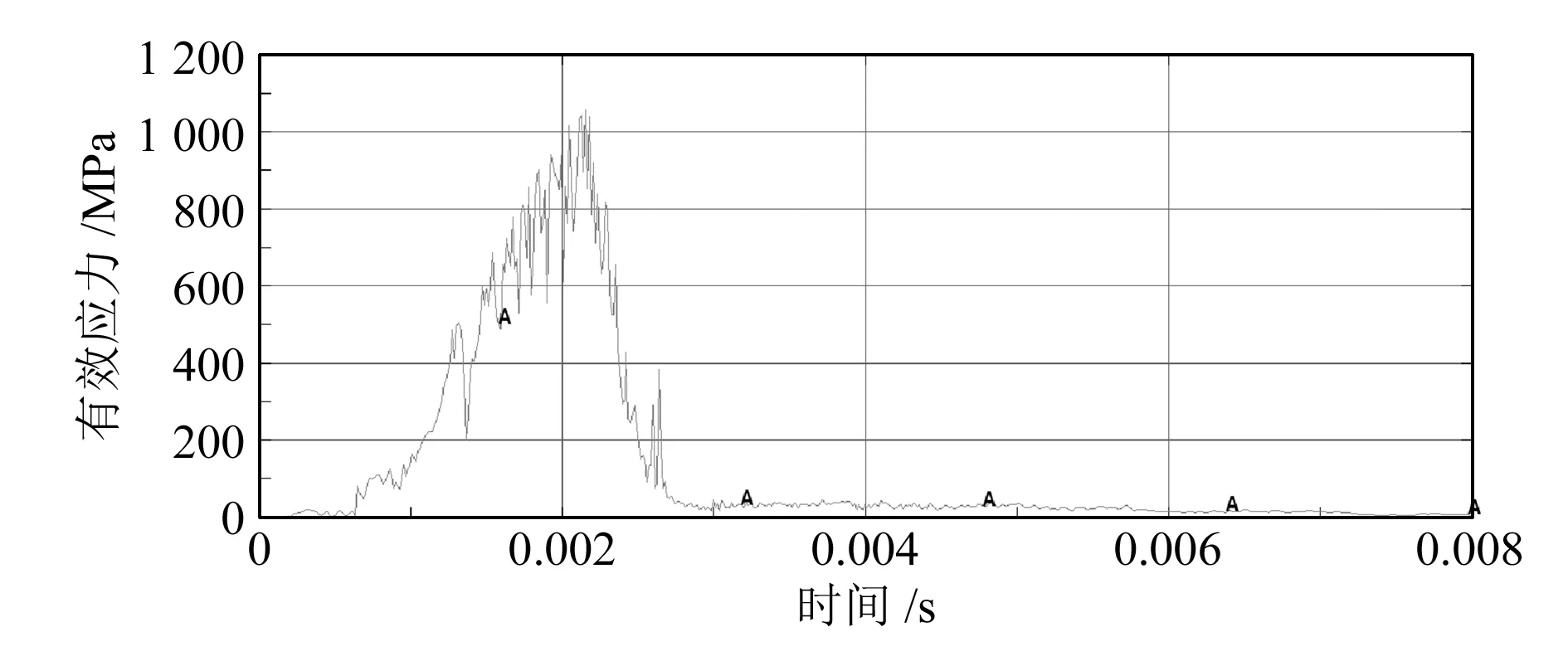
图5 锤头危险部位载荷时间历程

3 关键件疲劳寿命计算

3.1 疲劳寿命计算模型建立

1924年疲劳累积损伤[10]的概念被提出，到目前为止，疲劳累积损伤理论在疲劳寿命预测领域起着很重要的作用。当零件所承受的应力高于零件的疲劳极限时，零件会产生疲劳损伤，当疲劳损伤达到临界点时，零件会产生疲劳破坏，这就是疲劳累积损伤理论的基本模型[11]。线性疲劳累积理论认为疲劳损伤值是线性累积的，在同等应力条件下，每次加载所受到的损伤是相同的，低于疲劳极限的应力不会造成损伤，且疲劳寿命和加载次序无关。

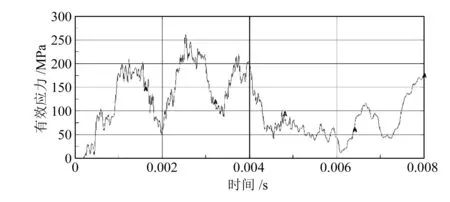
图6 锤轴危险部位载荷时间历程

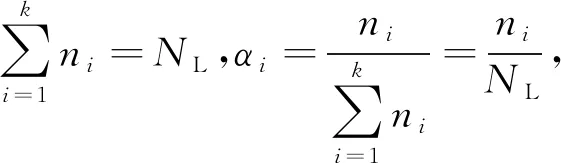
(5)

式中：d=(0.8～0.9)m，m为材料固有参数，为LgS-LgN双对数坐标中S-N曲线的反斜率；Si为载荷时间历程中对应的第i级应力幅值的应力；S1为最大级别应力水平；αi为第i级别应力出现次数占整个载荷历程的概率；NL为破碎机关键部位的疲劳寿命。

在破碎机工作过程中，被破碎物料种类复杂，其材料、厚度等相差较大，工况复杂，对有限元仿真而言，很难在仿真过程中模拟全部工况，因此可采用分段处理的方式。以废金属破碎过程中被破碎物料为例，当物料厚度小于2 mm时，采用2 mm厚度钢板代替，为第一档；当物料厚度为2～4 mm时，采用4 mm厚度钢板代替，为第二档，以此类推。由式(5)可得到第i档物料破碎时破碎机关键部位的疲劳寿命NLi。

记第i档物料占总物料比例为ηi，则

(6)

由于实际生产中，被破碎物料具有不同厚度，不同档位物料会消耗部分寿命，其所消耗的疲劳次数NSi可记为：

NSi=ηiNLi

(7)

则由仿真得到的总疲劳寿命NS为：

(8)

(9)

3.2 关键部位疲劳寿命估计

通过有限元仿真可以得到锤轴、锤头等危险部位的载荷-时间历程曲线，但连续的载荷-时间历程无法直接用于疲劳寿命的估算，需要利用计数法将其离散化。目前已有的计数法种类较多，使用最广泛的为雨流计数法[13]。

当被破碎物料厚度为8 mm时，采用雨流计数法离散破碎机锤头部位载荷，得到的载荷谱见表3。

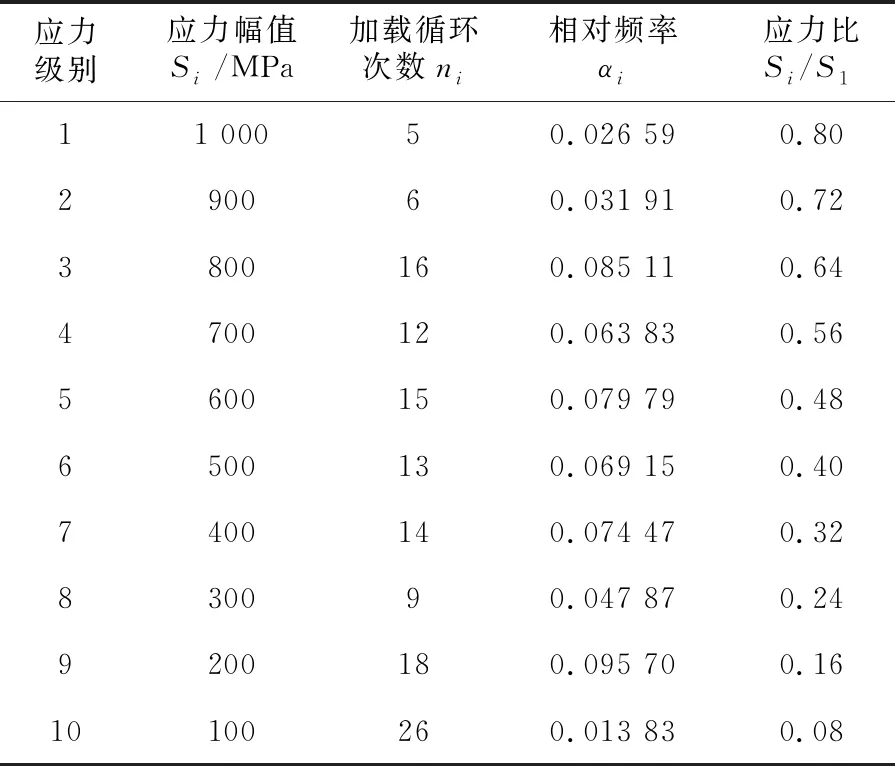
表3 破碎机锤头危险部位载荷谱

锤头所用材料为高锰合金钢Mn13-2，其疲劳极限为650 MPa，S1=1 250 MPa，N1=1×104，m=12.94，d=(0.8～0.9)m，本文中取d=0.85m。

将以上数据代入式(5)得：NL-8mm=3.048×106。

同理可得：NL-4mm=4.236×106，NL-6mm=3.858×106。

根据实际生产中废金属物料厚度统计可得ηi-4mm，ηi-6mm，ηi-8mm，取安全系数Q=1.5，将数据代入式(9)得:

(10)

破碎机主轴转动速度为n=600 r/min，因此锤头共可安全使用时间Nh为

(11)

对锤轴而言，计算得到其安全使用时间约为81.26 h。

根据破碎机生产商提供的数据，该破碎机在实际生产过程中，锤头与锤轴每7天会同时更换，破碎机每天工作10 h,因此其实际使用寿命为70 h。该数据与式(12)计算结果基本一致，这说明本文通过有限元分析对破碎机主轴部件的疲劳寿命估计正确，本文的研究可以对破碎机设计与优化起到一定的指导作用。

4 结束语

本文基于有限元分析技术，分析破碎机破碎过程中关键部位载荷，并基于科尔顿-多兰公式，考虑安全系数及不同工况疲劳寿命的问题，提出了适用于工程应用的疲劳寿命计算模型。

利用该模型，计算了破碎机关键部件锤头和锤轴部位的疲劳寿命，并与实际使用效果进行比对，证明可以较好预测破碎机关键部件疲劳寿命。本文的研究可为后续破碎机开发及安全分析提供较好的理论依据。