基于NSGA-Ⅱ的飞机襟翼运动机构多目标优化设计

陈 炎

(上海飞机设计研究院，上海 201210)

襟翼作为飞机增升装置的一部分，可以提高飞机的起飞、着陆性能，改善飞机进场速率、爬升率及进场飞行姿态[1]。为实现襟翼特定的运动轨迹需设计相应的运动机构。目前襟翼常用的运动机构有铰链式、四连杆式和滑轨-滑轮架式[2]。若襟翼运动机构设计不合理，将对飞机的气动性能及质量指标带来不利影响，因此对襟翼运动机构进行优化设计研究具有十分重要的意义。

国内外学者对襟翼运动机构展开了相关研究，文献[3]、[4]根据襟翼的运动轨迹分别通过解析法和几何法得到了襟翼运动机构的相关参数；文献[5]在考虑襟翼运动机构运动约束限制的基础上，对襟翼运动轨迹重新进行了优化分析；文献[6]对襟翼运动机构和襟翼气动外形进行了多目标优化，实现了在提升飞机气动性能的同时减少了襟翼运动机构的质量，但在优化过程中未考虑襟翼运动机构中滑轨质量的影响。

本文以襟翼运动机构中的滑轨-滑轮架式为例，以其运动学性能、动力学性能、质量指标为多目标优化函数，同时以运动机构的位移方程作为约束条件，利用带精英策略的非支配排序遗传算法(NSGA-Ⅱ)对襟翼运动机构进行优化设计，以提高襟翼运动机构的性能。

1 襟翼运动机构优化模型

1.1 襟翼运动机构工作原理及设计变量

滑轨-滑轮架式襟翼运动机构主要由曲柄、摇臂、滑轨、滑轮架组成，具体连接关系如图1所示。滑轨-滑轮架式机构的工作原理为：驱动器驱动曲柄转动，带动摇臂运动，使襟翼和滑轮架沿滑轨移动，并实现襟翼特定的运动轨迹。以曲柄绕驱动器转动的铰链点A为原点建立坐标系，运动机构设计参数可以通过图1中铰链点B点、C点的坐标Bi(xBi,yBi)、Ci(xCi,yCi)表示，其中i=1,2,3,分别代表B点、C点在襟翼巡航、起飞、着陆的位置。可以将该3个铰链点在襟翼巡航位置时的坐标作为本优化模型的设计变量X，即X={xA1,yA1,xB1,yB1,xC1,yC1}。

1.2 约束条件

襟翼的运动轨迹可以用襟翼在巡航、起飞、着陆位置时翼面上任意一点P的坐标及通过该点的某条直线与X轴之间的夹角表示，设P点在巡航、起飞、着陆时3个位置的参数为(xPi，yPi，θi)(i=1,2,3)。运动机构设计变量之间的约束关系可利用刚体导引机构的设计方法[7]得出，由于曲柄需绕驱动器旋转，曲柄坐标参数在襟翼巡航、起飞、着陆位置需满足定长约束方程：

(xBi-xA1)2+(yBi-yA1)2=(xB1-xA1)2+(yBi-yA1)2i=2,3

(1)

同时滑轮架在滑轨上平移，滑轮架坐标参数在襟翼巡航、起飞、着陆位置需满足定斜率约束方程：

(2)

Bi和Ci点在襟翼巡航、起飞、着陆位置的坐标由坐标变换关系确定：

(3)

(4)

式中：D1i为刚体位移矩阵，由P点的位置参数确定：

i=2,3

(5)

为保证滑轮架的安装空间，铰链点C1到襟翼弦线beg的距离lcb需满足相应约束条件，即

lcb≥d

(6)

式中：d为lcb下限约束。

运动机构设计变量还需满足边界约束条件：

lb≤X≤ub

(7)

式中：lb和ub分别为变量X的下限和上限约束。

1.3 目标函数

目标函数根据实际优化目标进行选取，优化目标的侧重点不同，目标函数的选取也不同。对于襟翼运动机构来说，除了要实现襟翼特定的运动轨迹，还要考虑其对飞机质量、气动阻力的影响，具体如下：

1)襟翼运动机构的质量。

襟翼运动机构的质量越小越有益于飞机的经济性。襟翼运动机构主要由曲柄、摇臂、滑轨、滑轮架组成，为了简化目标函数，假设这些零件的材料密度和截面面积一致，因此襟翼运动机构的质量可由上述零件的长度之和函数f1(X)表示，即

f1(X)=|B1-A1|+|C1-B1|+|D13C1-C1|

(8)

式中：A1,B1,C1为3个铰链点在襟翼巡航位置时的坐标。

2) 襟翼运动机构的气动阻力。

襟翼运动机构位于机翼后缘处，为实现襟翼的运动，其高度通常比翼盒的高度高，因此会对飞机气动效率带来不利影响：运动机构高度越高，其迎风面积越大，导致飞机气动阻力增大，飞机气动效率降低。襟翼运动机构的气动阻力可由襟翼运动机构的高度函数f2(X)表示，并且实际高度由摇臂的长度和滑轨最低点的位置决定，即

f2(X)=max[|B1-A1|,|L·D13C1|]

(9)

式中：L=[0 1 0]。

3) 襟翼运动机构的驱动载荷。

襟翼运动过程中运动机构由驱动器提供的驱动载荷M驱动。M越大，驱动器的设计成本和质量越大，从减少飞机设计成本和减重角度出发，在整个襟翼运动过程中M的峰值应越小越好。

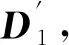
M+F·lAF=T·lAT

(10)

式中：lAF,lAT分别为A点到气动载荷方程F和支撑力方程T的距离。

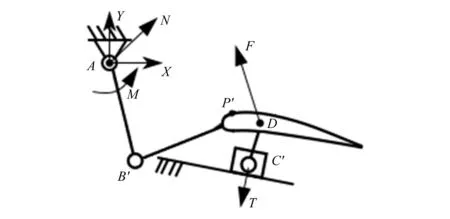
图2 襟翼运动机构受力示意图

再对B′点取力矩平衡，得

F·lB′F=T·lB′T

(11)

式中：lB′F，lB′T分别为B′点到气动载荷方程F和支撑力方程T的距离。

根据方程(10)、(11)，驱动载荷可表示为

(12)

假设气动载荷F为已知量，驱动载荷M可由等效驱动力臂函数f3(X)表示，即

(13)

2 襟翼运动机构优化实例分析

由第1章可以看出，襟翼运动机构优化是一个典型的多变量、多目标的优化问题，3个目标函数都很重要，关系到襟翼运动机构的质量、气动性能，还会影响飞控系统的驱动能力。如果对此问题采用传统的多目标优化算法，不但求解速度慢、效率低，同时还会依赖目标函数中权重参数的选取。文本选用了带精英策略的非支配排序遗传算法[8](NSGA-Ⅱ)进行优化，该算法具有收敛速度快、鲁棒性好、稳健性强等特点，已成功应用于多目标优化领域。由于优化过程涉及非线性约束条件，导致计算效率下降，因此本文采用了二元锦标的约束处理方法[9]，加快了计算收敛速度。

设置NSGA-Ⅱ算法的优化参数为：最前端系数为0.3、种群大小为200、进化代数与停止代数均为200、交叉概率为0.8、变异概率为0.01、适应度函数值偏差为1×10-4，其余输入参数值见表1。根据以上参数绘制Pareto前端，结果如图3所示。

从图3中可以看出，每个点对应一个 Pareto最优解，各 Pareto最优解之间没有优劣之分。针对各 Pareto最优解，可以根据经验和对各目标的重视程度从中选出最满意的解，并与原始设计进行对比，对比结果见表2。

表1 输入参数清单

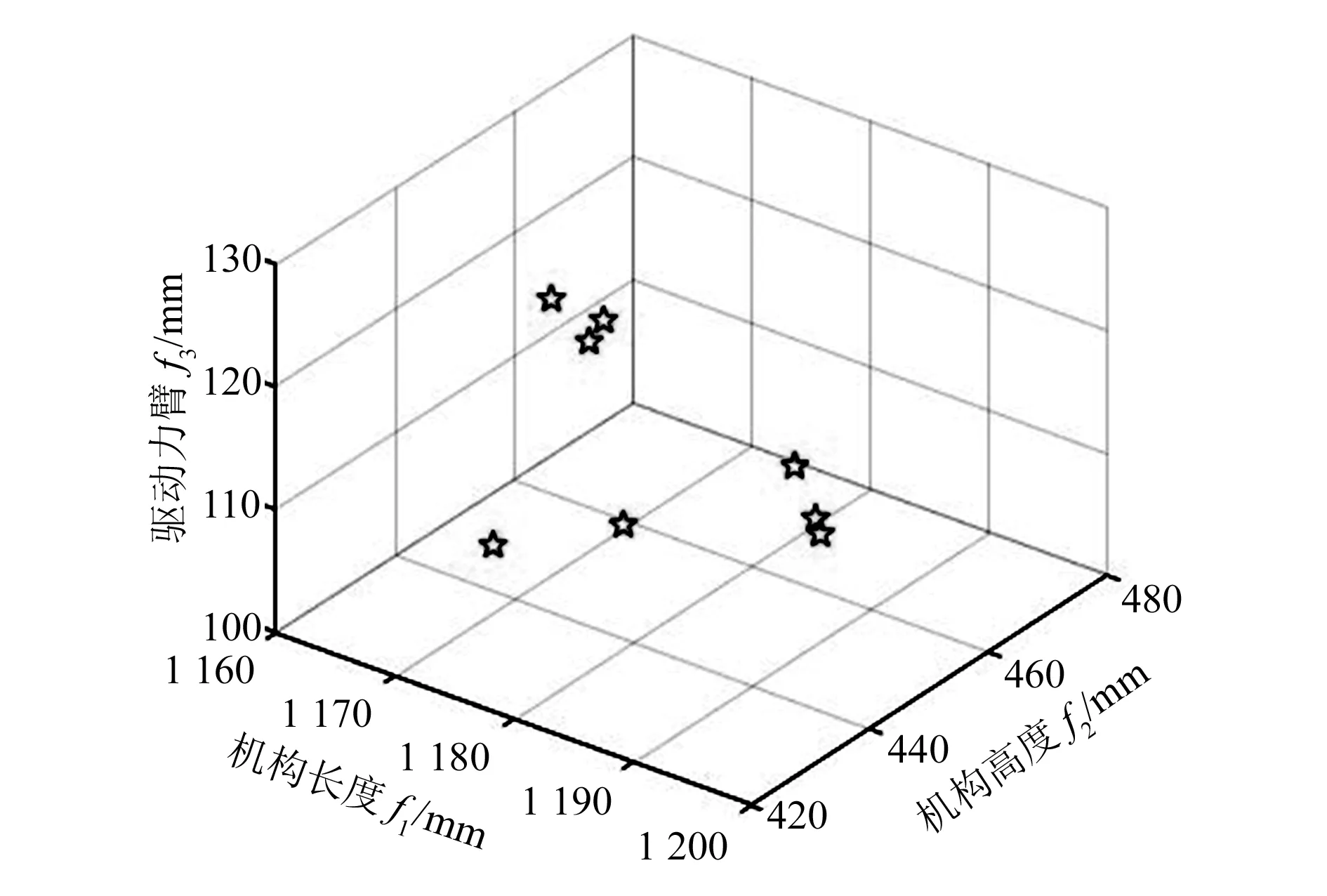
图3 Pareto最优解集示意图

表2 所选优化方案与原始设计对比

从表2的对比中可以看出，选出的Pareto最优解与原始设计数据相比3个目标都有一定程度的改善，优化后的襟翼运动机构质量减少了3.9%，气动阻力减少了0.69%，驱动载荷峰值减小了15.4%。

3 结束语

本文采用NSGA-Ⅱ优化算法对襟翼运动机构进行多目标优化，并根据襟翼运动机构的运动特点设定约束条件，优化结果表明，襟翼运动机构在满足襟翼运动轨迹的前提下，能有效降低飞机质量，改善飞机气动性能，降低飞机设计成本。本文为襟翼运动机构初始设计和多目标优化提供了一种分析方法，也为后续进行深入研究提供了参考依据。