基于桁架结构优化的复杂零件构型设计方法
2020-12-01马雅丽牛金月
马雅丽,牛金月,梁 晨
(大连理工大学机械工程学院, 辽宁 大连 116024)
复杂零件是机器的重要组成部分,其结构设计的合理性直接影响机器的整体性能和被加工件的品质,该类零件质量大、结构复杂,如箱体、立柱等,高性能、轻量化、低成本的零件结构设计方法一直是研究的热点[1]。
多年来,众多学者在结构优化设计方面做了大量工作。周奇才等[2]将连续体拓扑优化和离散体拓扑优化相结合,实现了桁架结构的拓扑布局和尺寸优化,以克服传统基结构设计方法对最优解的束缚。高阁[3]、史航[4]构建了任意形状区域的桁架基结构并对其优化,以桁架结构替代连续体结构对经纬仪的关键部件进行结构设计。张兴朝[5]、徐燕申等[6]基于元结构的概念对机床大件进行结构设计。Ma等[7]提出了一种复杂零件力-性能-结构映射的结构拓扑和尺寸协同优化的轻量化设计方法,实现了复杂零件性能最优的结构构型及尺度设计。这些研究成果为复杂零件结构设计方法的研究打开了新的视野。
桁架结构是由多根小截面杆件组成的“空腹式大梁”,广泛应用于建筑、工程机械、航空航天等领域。为高效、便捷地获得具有最佳性能的复杂零件结构构型,本文提出了一种基于桁架结构优化的复杂零件构型设计方法,可在满足零件性能需求的前提下实现轻量化设计。
1 基于基结构法的桁架结构设计
桁架结构优化以杆件横截面积作为优化设计变量,通过删除横截面积小于阈值的杆件,将拓扑优化问题转化为带有边界约束的尺寸优化问题,以达到桁架拓扑结构和尺寸同步设计的目的。优化求解时,使用混合粒子群算法对结构全局寻优,获得性能最佳结构构型。
1.1 基结构
基结构是桁架优化的初始结构,基结构法[8]是目前广泛使用的一种桁架优化方法。根据设计域的形状和边界条件,按照某些准则布置一系列的离散节点,将节点以杆件连接得到的桁架集合称作基结构,通过建立基结构进行桁架优化的方法称作基结构法。
1)单元基结构。
单元结构是一些外形变化不大、内部结构相对独立的结构,其是构成桁架结构的基本单位。基结构是包含设计域内可能存在的所有杆件的结构,换言之,最优解是基结构的子集。
基结构的建立以有限元网格法为基础,将有限元网格节点作为基结构的节点,连接节点即可获得基结构。本文的基结构设计域为正方形,采用数量为2×2(即两行两列)的正方形网格对单元划分,所有节点以杆件连接得到基结构。单元基结构的建立过程如图1所示。
2)桁架基结构。
整体经过分解后可得到单元。面积大、形状不规则的整体可分解为若干单元,在各单元内建立的基结构称作单元基结构,单元基结构组成的整体称作桁架基结构,桁架基结构按照一定的算法进行优化得到的优化结构称作桁架结构。整体的分解应考虑其外形特点、尺寸大小和使用功能等,根据设计经验,需遵循以下原则:
①分析设计域几何形状边界特征,保证划分后的形状边界为矩形。初始设计的区域划分时,长宽比尽量接近1。图2所示为一不规则形状划分区域生成桁架基结构示例。
②考虑零件的性能及工艺性,一般选取铸件单元尺寸为300~500 mm,用户可根据实际条件适当调整。但为了保证制造工艺性及结构性能,以下界不小于200 mm、上限不大于600 mm为宜。
1.2 单元结构优化设计
1)优化数学模型。
考虑N个杆件的基结构在多工况下的优化情况,以单元结构总质量最轻为优化目标,杆件截面积为优化变量,单元基结构节点最大位移的最小值小于约束值为约束,构建单元基结构优化模型为:
(1)
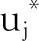
结构优化时,给定杆件尺寸上下界,删除截面尺寸小于阈值的杆件。由于杆件尺寸是动态变化的,优化结构确定时,杆件尺寸优化也同步完成,从而实现了结构与尺寸的同步设计。
2)优化有限元模型。
采用有限元法在MATLAB环境中建立单元基结构模型,指定杆件类型为欧拉梁,有限元模型为:
(2)
(3)
式中:Ke为杆件的刚度矩阵;B为杆件的几何矩阵;E为材料的弹性模量;Ω为杆件体积;ue为节点位移矢量;Fe为节点力矢量。
单元基结构由杆件组装而成,其有限元模型为:
(4)
(5)
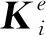
3)优化模型求解算法。
本文采用的混合PSO算法将基本PSO算法和不同选择机制相结合,在提高收敛速度的同时保证了全局搜索能力。后代粒子的位置和速度如下:
(6)

4)单元结构优化。
优化时取基结构边界杆件为非设计域,仅对单元结构内部的杆件进行删减。传统的基结构法在优化过程中仅删除节点之间的杆件,但事实上建立基结构时杆件与杆件搭接产生了“交点”,且过“交点”的杆件并无约束关系。为扩大最优解的搜索空间,本文的最优解由基结构中节点和杆件“交点”共同决定。简言之,杆件“交点”虽不作为基结构生成的节点,但作为优化节点。
1.3 桁架结构优化设计
桁架结构可分解为若干单元结构,采取单元重组的方式对桁架结构优化,即对组成桁架结构的各单元结构分别优化,再将单元结构组合,以获得桁架结构的最终结果。
桁架结构优化的关键是对边界条件的确定,桁架结构优化后的结构与力从载荷到约束的传递路径一致。组成桁架结构的两相邻单元结构共用同一个杆件,通过杆件上的节点将载荷传递到下一个单元。单元结构之间的内力可通过载荷等效和力的平移定理确定。图3为桁架结构优化流程图。
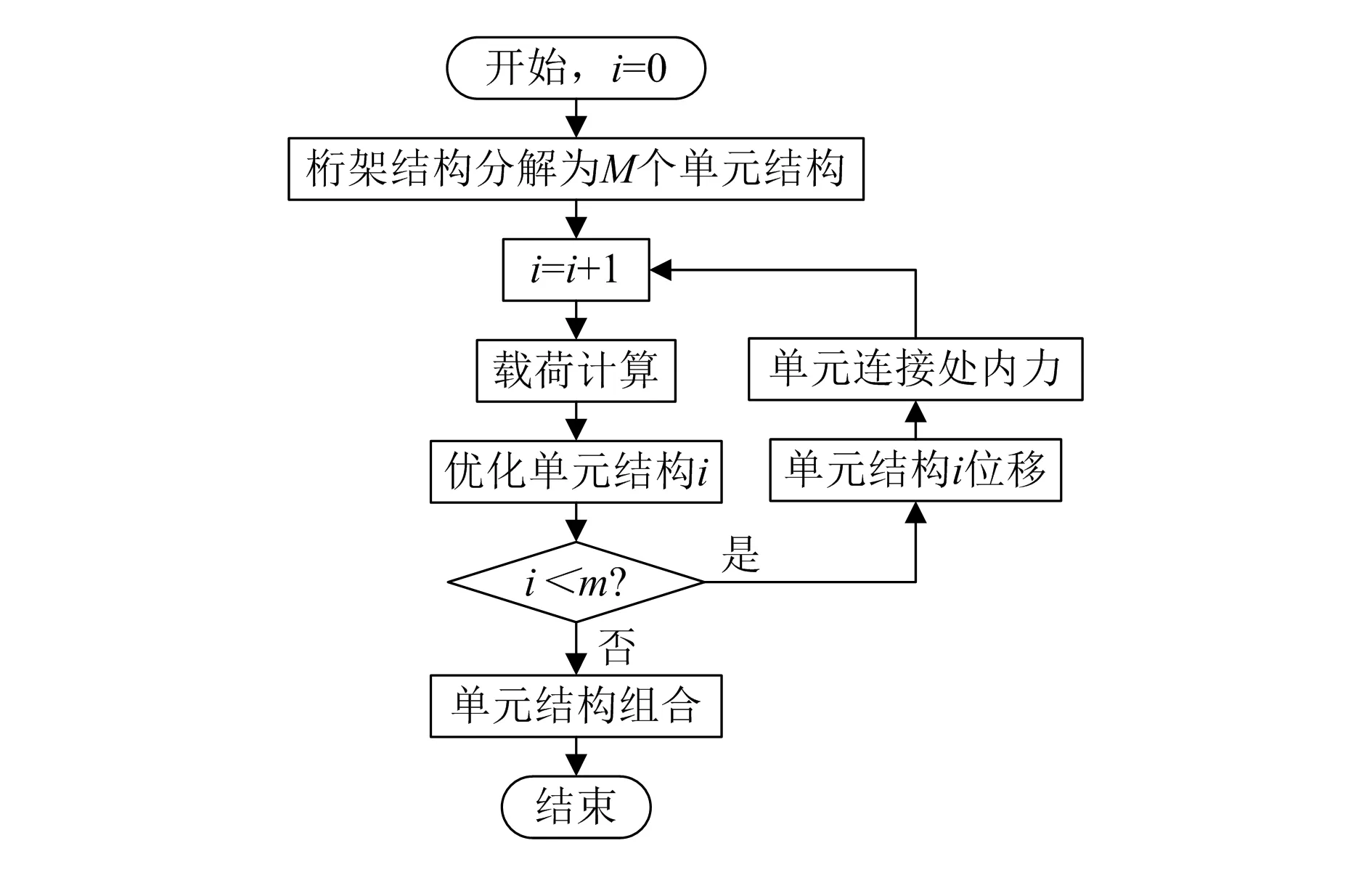
图3 桁架结构优化流程图
为简单而不失一般性,以两个单元结构组成的桁架结构(图4所示)为例详述设计过程,具体步骤如下:
1)外载荷计算。利用力的平移定理将载荷等效为桁架结构可用的节点力,并作用到各单元。
2)1号单元结构优化设计。1号单元与2号单元共用同一杆件,为固定连接,1号单元优化时暂将该固定连接处等效为全约束。
3)2号单元结构优化设计。1号单元构型已知,通过刚度方程计算1号单元与2号单元固定连接处内力,此内力以外载荷形式作用到2号单元上,2号单元设计时将其与下一个单元或底座的连接处等效为全约束。
4)重复步骤2)、3),对余下单元结构进行优化,若单元结构到此结束,则完成计算。
5)将各单元优化结果组合,完成桁架结构优化。
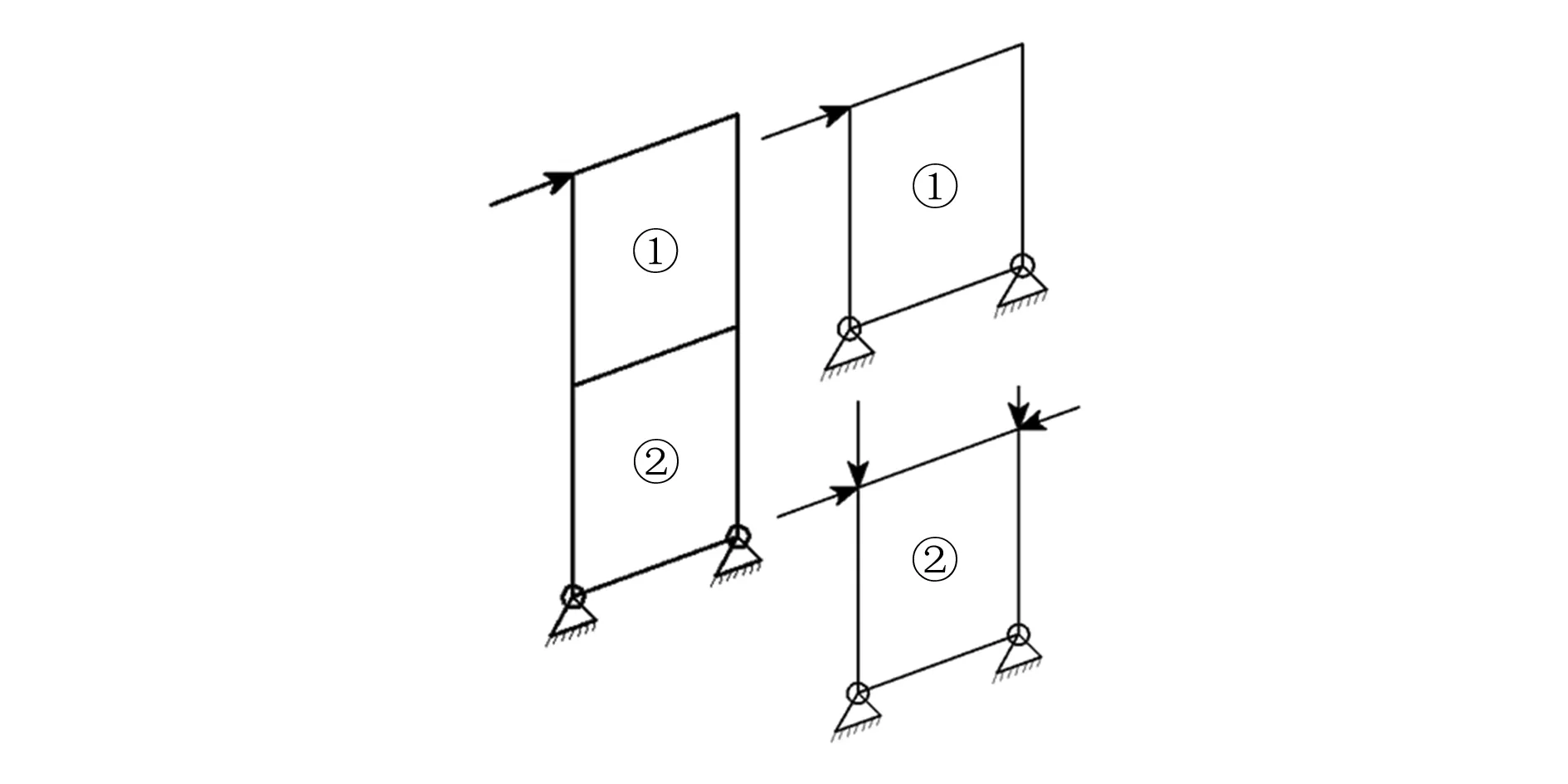
图4 桁架结构示意图
2 基于桁架结构优化的零件构型设计
复杂零件的受力状态与桁架结构有所不同,因此利用桁架结构进行零件构型设计时,要对载荷等效处理。另外,零件一般为空间结构,构型设计前需确定零件构型的设计域。
2.1 载荷等效
零件实际工作情况下,所受载荷一般为均布载荷或集中载荷,而桁架结构仅在桁架平面内承受节点力,因此需对载荷进行等效处理。载荷等效的含义是等效节点载荷引起的节点位移与非节点载荷引起的节点位移相同。杆件受力简图如图5所示。

图5 杆件受力示意图
基于有限元理论,根据外力功的计算公式计算节点载荷等效值:
(7)
式中:We为外力功;p(x)为杆所受压强;l为杆单元长度;N(x)为单元的形状函数;FPA,FPB为节点力;MA,MB为弯矩;qe为节点位移阵列。
2.2 复杂零件构型设计
1)零件构成及设计域的确定。
复杂零件根据结构特点可以分解为由外部形状确定的主体框架、支承结构以及其他结构构成的整体。以机床立柱为例,该零件是在主体框架的基础上增加支承结构和其他结构构成,如图6所示。主体框架指的是形成零件的基本几何形状。支承结构是起主要支承作用的结构。其他结构包括壁板、加强筋类结构、导轨、螺栓孔、散热槽和出砂孔等,这些结构的种类和尺寸等根据零件用途和功能决定。
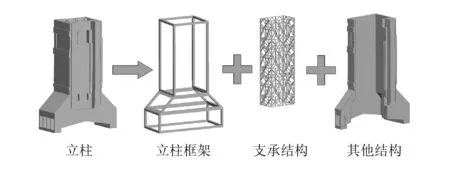
图6 复杂零件构成
本文的设计方法是对零件的支承结构设计,亦称复杂零件构型设计,零件的主体框架是零件构型设计域的边界,框架内部为零件构型的设计域。
2)零件构型设计。
零件的构型设计均在主体框架平面内进行。结构构型具有承载并传递力的作用。
对于二维平面内的支承结构,可基于桁架结构的设计方法设计,即载荷等效后直接进行构型设计,如图7中(a)所示的机床床身。对于框架类零件或箱体类的复杂零件,设计域常包含多个空间平面,此时要将三维问题降为二维问题,然后在二维平面内进行结构设计,图7(b)所示是将一个机床立柱的构型设计降解为4个设计域平面。

图7 复杂零件构型设计
零件支承结构的构型设计要依据桁架结构分解的原则,将设计域分解为若干个单元,分别优化再组合,方能完成整个零件的构型设计。
3 基于桁架结构优化的零件构型设计实例
利用本文方法,以某立式加工中心立柱为例进行结构优化设计,并与拓扑优化设计方法得到的结构进行对比,以验证本文方法的有效性。
3.1 零件构型设计
1)桁架基结构建立。
该零件主体框架如图8所示,主体框架的边界即设计域的边界,在设计域内进行支承结构构型设计。
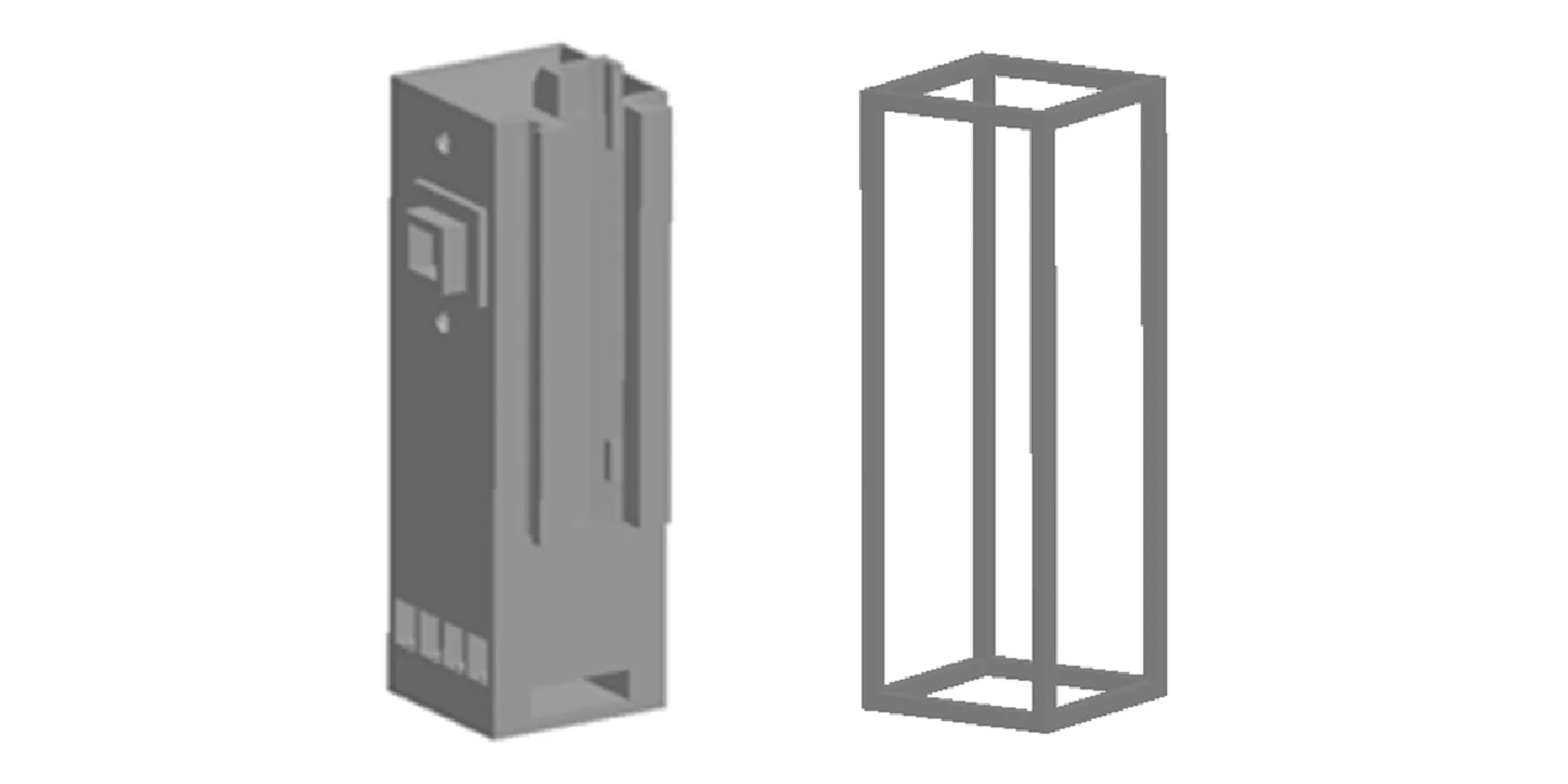
图8 主体框架图
该支承结构由4个区域构成,各区域均为1 500 mm×500 mm的四边形,单元划分结果如图9所示。在MATLAB环境下建立基结构,并将零件的载荷条件转化为桁架结构优化可用的节点力,为后续构型设计做准备,在此不赘述。
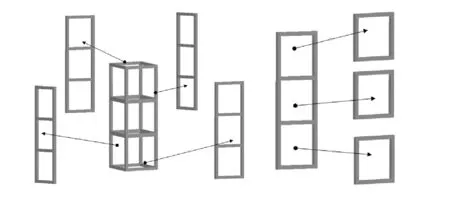
图9 立柱支承结构单元划分
2)立柱构型设计。
分别对4个设计域内的支承结构进行结构优化,最终结构构型如图10所示,杆件截面尺寸为40 mm×40 mm。
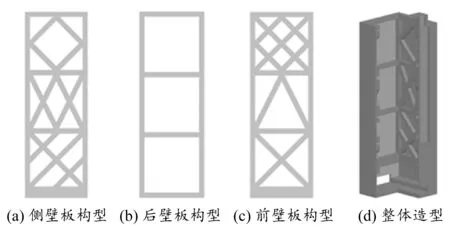
图10 立柱设计结果
3.2 结构方案对比分析
设计完成后,利用有限元软件ANSYS分析立柱的静态变形,并将结果与拓扑优化方法得到的立柱性能进行对比,比较结果见表1。本文方法设计的立柱质量为983 kg,较拓扑优化结果减轻5.4%,综合变形为0.052 mm,较拓扑优化结果减小10.28%。上述结果表明,本文的设计方法能实现零件的轻量化设计和结构优化设计,方法合理、有效。
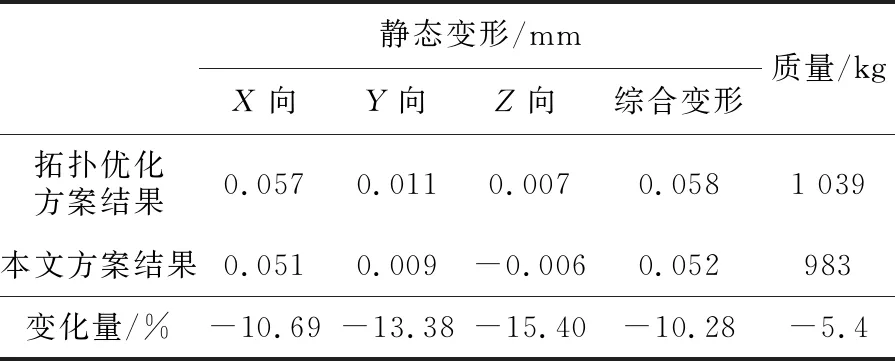
表1 零件性能对比表
4 结束语
本文提出的基于桁架结构优化的复杂零件设计方法可实现零件结构构型和尺寸的同步设计,在简化结构设计过程的同时满足结构性能需求。通过单元划分的方法构建基结构,有效减少了基结构的生成时间,在减少计算量的同时最大限度地寻求最优解。采用本文提出的方法优化设计的立式加工中心立柱质量为983 kg,较拓扑优化方案减轻5.4%,综合变形为0.052 mm,较拓扑优化方案减小10.28%,在强化性能的同时实现了立柱的轻量化设计。
