多传感器组合导航系统的改进多尺度滤波算法

林雪原，孙玉梅，董云云，乔玉新，陈祥光,2

1. 烟台南山学院 电气与电子工程系，烟台 265713 2. 北京理工大学，北京 100081

多传感器组合导航系统有两项重要指标，即可靠性与精度。为了提高系统的可靠性，可以从子导航传感器[1-2]及系统融合[3]加以考虑。解决多传感器系统的信息融合问题，进而提高系统的导航精度，目前有两种途径：一种是集中式卡尔曼滤波，另一种是分散化卡尔曼滤波。集中式卡尔曼滤波具有计算负担重以及容错性能差的缺点，而分散化滤波在多传感器组合导航系统中得到了广泛应用[4-5]，其中Carlson提出的联邦滤波器(下面简称算法1)受到了重视[6]。

以上算法都是基于系统在时域的动态模型和观测模型上建立起来的，并没有考虑到系统的多尺度特性。随着多尺度系统理论的不断发展，将小波分析与卡尔曼滤波技术相结合形成多尺度卡尔曼滤波算法得到发展[7-9]，并在目标跟踪领域及图像处理领域得到验证[10]。其工作的基本思想大都是先将系统的动态方程和观测方程改写成以数据块形式描述的状态方程和观测方程(即状态方程是块状态向量与块状态向量的关系，而量测方程是块观测向量与块状态向量的关系)，从而再套用经典卡尔曼滤波算法与小波分析相结合对相关的块状态向量进行处理， 试验表明该方法相对于现有状态估计方法可以以更高的精度来估计系统状态。组合导航系统滤波模型相对于目标跟踪模型而言，具有状态方程复杂且维数较高、滤波耗时高等特点，文献[11-12]成功地将多传感器组合导航系统与多尺度卡尔曼滤波相结合，进而得到精度更高的滤波精度。然而上述方法存在如下问题：块状态向量间各向量的噪声是相关的，滤波器的实时性得不到保证[8]。

为了克服上述问题、优化多传感器组合导航系统的多尺度滤波算法，本文首先将系统原始状态方程表达为块状态向量的形式，然后将实时获得的量测向量表达为块状态向量的方程进而解决估计器的实时性问题，并描述了滤波算法的详细步骤，最后以SST(天文导航)/GPS(全球导航定位系统)/SINS(捷联惯性导航系统)组合导航系统为例对本文算法进行了仿真与验证。

1 系统描述

给定一类有单个动态模型和多个测量模型组成的动态系统：

x(k+1)=A(k)x(k)+G(k)w(k)

(1)

zi(k)=Hi(k)x(k)+vi(k)，i=1,2,…,N0

(2)

式中：k为离散时间指标；x(k)∈Rn×1为目标状态向量；A(k)∈Rn×n为系统状态转移矩阵；G(k)∈Rn×m为系统噪声矩阵；w(k)∈Rm×1为系统噪声，它是一个高斯白噪声序列，并满足：

E{w(k)}=0，E{w(k)wT(j)}=Q(k)δkj

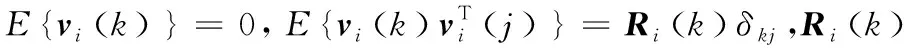
系统(1)的初始状态x(0)是一个随机向量，并具有如下统计特性：

(3)

假定x(0)、w(k)、vi(k)之间是相互统计独立的。

1.1 分块描述

将系统(1)表示为状态块的形式，以便对系统进行多尺度分析，定义块长为M的状态块：

X(m+1)=[xT(m+1,1),xT(m+1,2),…,

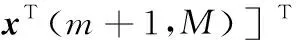
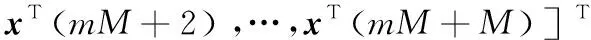
(4)

式中：m=0,1,2,…；M=2i(i=1,2,3,…)。

而状态块X(m+1)中的第s(s=1,2,…,M)个元素为：

x(m+1,s)=x(mM+s)=

A(mM+s-1)x(mM+s-1)+

G(mM+s-1)w(mM+s-1)=…=

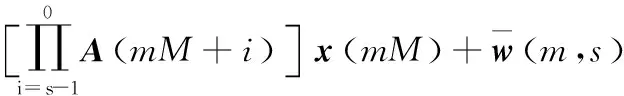
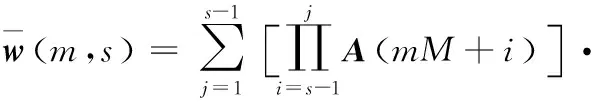
G(mM+j-1)w(mM+j-1)+

G(mM+s-1)w(mM+s-1)

相应的过程噪声块向量为：

并可表示为：

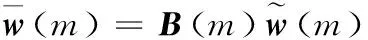
B(m)的第r行第c列元素用Br,c(m)表示，则B(m)的各元素表示为：

根据以上定义和符号，状态向量模型(1)可重新描述为：

(5)

其中:

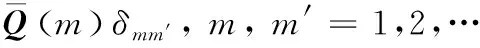
(6)

式中：

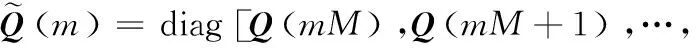
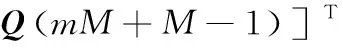
测量模型(2)可进一步表示为：

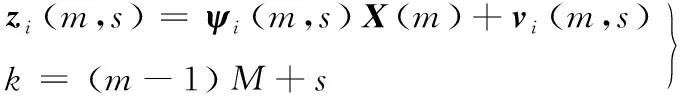
(7)

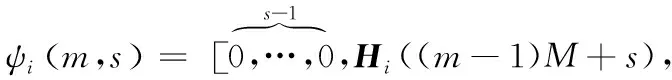
因此，式(7)就建立了每个时刻的测量值zi(m,s)与状态块X(m)之间的关系，这样就为算法的实时性提供了可能，并将能克服已有算法中存在半实时性的不足。

1.2 离散小波变换

多尺度分析是将待处理信号用小波变换的方法在不同的尺度上进行分解，分别得到粗尺度上的平滑信号与细尺度上的细节信号[10]。

如果将尺度i上向量序列x(i,k)∈Rn×1(k∈Z)表达成数据块的形式：

Xi,V(m)=Xi(m)=

[xT(i,(m-1)Mi+1),

xT(i,(m-1)Mi+2),…,

xT(i,(m-1)Mi+Mi)]T

式中：Mi=2i-1。则小波变换的分析算子与综合变换算子表达如下：

Xi,V(m)=Hi·Xi+1,V(m)，L≤i≤N-1

(8)

Xi,D(m)=Gi·Xi+1,V(m)，L≤i≤N-1

(9)

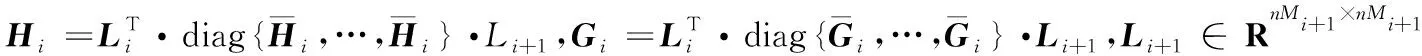
对应的多尺度重构变换为:

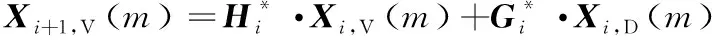
(10)

“*”表示复矩阵的共轭转置，若记

γ(m)=[(XN-1,D(m))T,(XN-2,D(m))T,…,

则与式(8)(9)相对应的多尺度分解可进一步表示为:

γ(m)=WX·X(m)

(11)

式中：WX为矩阵算子，

容易验证WX是一个正交矩阵，即：

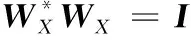
(12)

而式(10)可表示为:

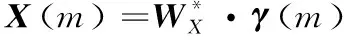
(13)

2 分块系统的多尺度滤波方法

首先，将小波算子WX同时作用于方程(5)两边：

我院2016年5月--2017年9月收治的64例行口腔修复患者,按照随机数字表法分为实验组和对照组,每组患者32例。实验组:男16例,女16例,年龄42-76岁,平均年龄(58.5±14.5)岁,病程1-5周,平均病程(2.5±0.5)周;对照组:男17例,女15例,年龄43-78岁,平均年龄(60.5±15.5)岁,病程1.5-5周,平均病程(3.25±0.75)周。将两组患者基本资料进行精细对比分析,差异不明显(P>0.05),具有临床可比性。所有患者均自愿入组并签署知情同意书。

(14)

再利用式(11)(12)，式(14)就又改写成：

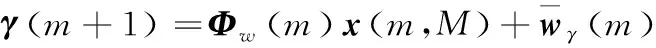
(15)

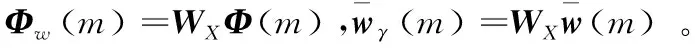
利用式(12)，观测向量模型(7)可以等价描述为：

zi(m,s)=ψi,w(m,s)γ(m)+vi(m,s)

(16)

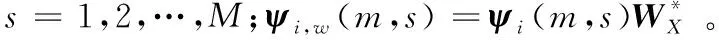
下面将从初始条件(3)出发，基于多尺度模型(15)(16)，建立具有同步多传感器系统多尺度序贯卡尔曼滤波器。为此，先引入来自所有传感器的1～m块的测量值集合[7]：

其中:

Z(l)={Z(l,1),Z(l,2),…,Z(l,M)}=

{Z1(l),Z2(l),…,ZN0(l)}，l=1,2,…

l=1,2,…，s=1,2,…,M

Zi(l)={zi(l,1),zi(l,2),…,zi(l,M)}，

i=1,2,…,N0

下面以第m个状态块为例，从两个层次上来说明对状态块进行估计的过程。

假设已经完成下列工作：

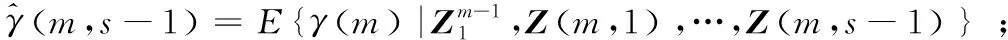
3)在第m块中的第s个点处，已完成了基于z1(m,s)，z2(m,s)，…，zi-1(m,s)对γ(m)的估计，即：

Z(m,s-1),z1(m,s),…,zi-1(m,s)}

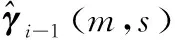
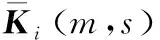
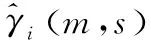
利用逆小波变换，可以得到目标状态块X(m)的估计值及其误差协方差矩阵：

m=1,2,…，s=0,1,2,…,M，i=1,2,…,N0

s=0,1,2,…,M，i=1,2,…,N0

应该注意到：

1) 当s=0，i=0时，

2)当s=M，i=N0时，就得到式(15)中γ(m)的最终估计值及误差协方差矩阵：

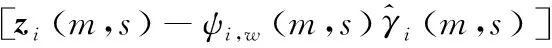
(17)

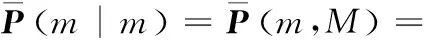
(18)

利用逆小波对式(17)和式(18)作变换，进而得到状态块X(m)的估计值及其误差协方差矩阵：

3 仿真及分析

为验证本文所提的改进多尺度滤波算法的有效性，将算法用于GPS/SST/SINS组合导航系统。滤波器的误差方程经降阶后，状态向量取为[14-15]：

x(t)=[φE,φN,φU,δvE,δvN,δL,δλ,εrx,εry,εrz]T

式中：下标E、N、U代表地理坐标系的东、北、天方向；δL,δλ为纬度、经度误差；δvE,δvN为速度误差；φE,φN,φU为数学平台误差角；εrx,εry,εrz为陀螺一阶马尔科夫漂移误差，量测方程及方程其他参数详见文献[11-12，14]。仿真中各传感器误差参数设置如表1所示。

表1 导航传感器误差参数

下面的仿真试验中，GPS、SST的采样周期均设定为1 s，SINS的采样周期设定为0.02 s；综合考虑滤波精度与滤波实时性因素，式(4)中取M=2，所采用的小波为Haar二进制小波。为了便于对基于本文改进算法及基于算法1的滤波精度进行比较，对相同的SINS、GPS、SST仿真数据，本文同时进行了基于两者算法的滤波分析，其中图1～图6分别给出了位置、速度与姿态误差对比曲线、图7给出了系统仿真轨迹、图8给出了两种算法的计算量对比。

表2及表3给出了基于上述两种滤波算法的导航结果数据统计值。

图1 基于改进算法的位置误差Fig.1 Position error based on the improved algorithm

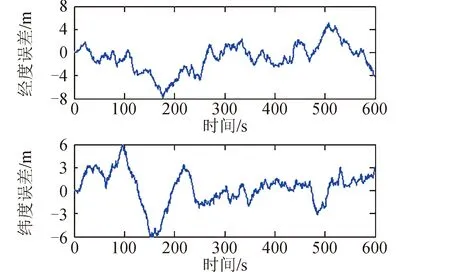
图2 基于算法1的位置误差Fig.2 Position error based on algorithm 1

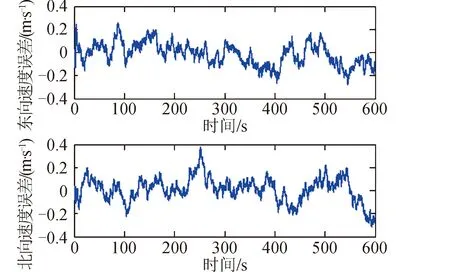
图3 基于改进算法的速度误差Fig.3 Velocity error based on the improved algorithm

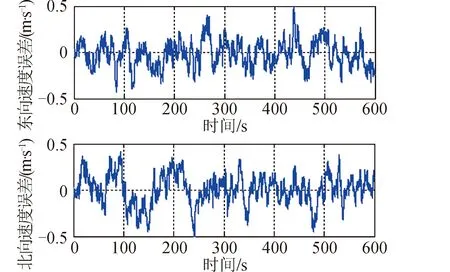
图4 基于算法1的速度误差Fig.4 Velocity error based on algorithm 1

图5 基于改进算法的姿态误差Fig.5 Attitude error based on the improved algorithm

图6 基于算法1的姿态误差Fig.6 Attitude error based on algorithm 1

在Intel Core 2 Duo P7350 2.0G 45 nm处理器的环境下，从表3可以看出改进算法的滤波平均时间约为0.07 s，算法1的滤波平均时间约为0.033 s；在相同的环境下、对相同的多传感器组合导航系统模型，文献[12]算法的滤波平均时间约为0.094 s，而改进算法与文献[13]算法的滤波精度相同。

在式(4)所示的模型中，适当增加块向量内向量的个数时，即M=4,8,…时，导航参数的精度将会进一步提高，但滤波所有的时间将会大幅增加，因此，M=2时即能够保证滤波的精度又能够保证滤波的实时性。

图7 仿真飞行轨迹Fig.7 Simulated flying trajectory

图8 本文算法与算法1的计算量对比Fig.8 Comparison of computation burden between this paper′s algorithm and algorithm 1

4 结束语

将系统原始状态方程表达为块状态向量的形式，并将实时获得的量测向量表达为块状态向量的函数，采用SST/GPS/SINS组合导航系统为例对本文算法进行了仿真与验证，得出如下结论：

1)相对于算法1，本文算法对位置精度可提升一倍以上，速度精度可提升10%，姿态精度略有提升。产生的原因是组合导航系统是一个典型的非线性系统，而经过滤波后的误差修正采用的是反馈校正方法，即对位置、速度采用线性修正、而对姿态采用非线性修正方法。本文所提的改进算法优于算法1的原因是：改进算法采用分块估计与小波变换相结合的方法，块状态向量的估计值中包含了状态的平滑值。

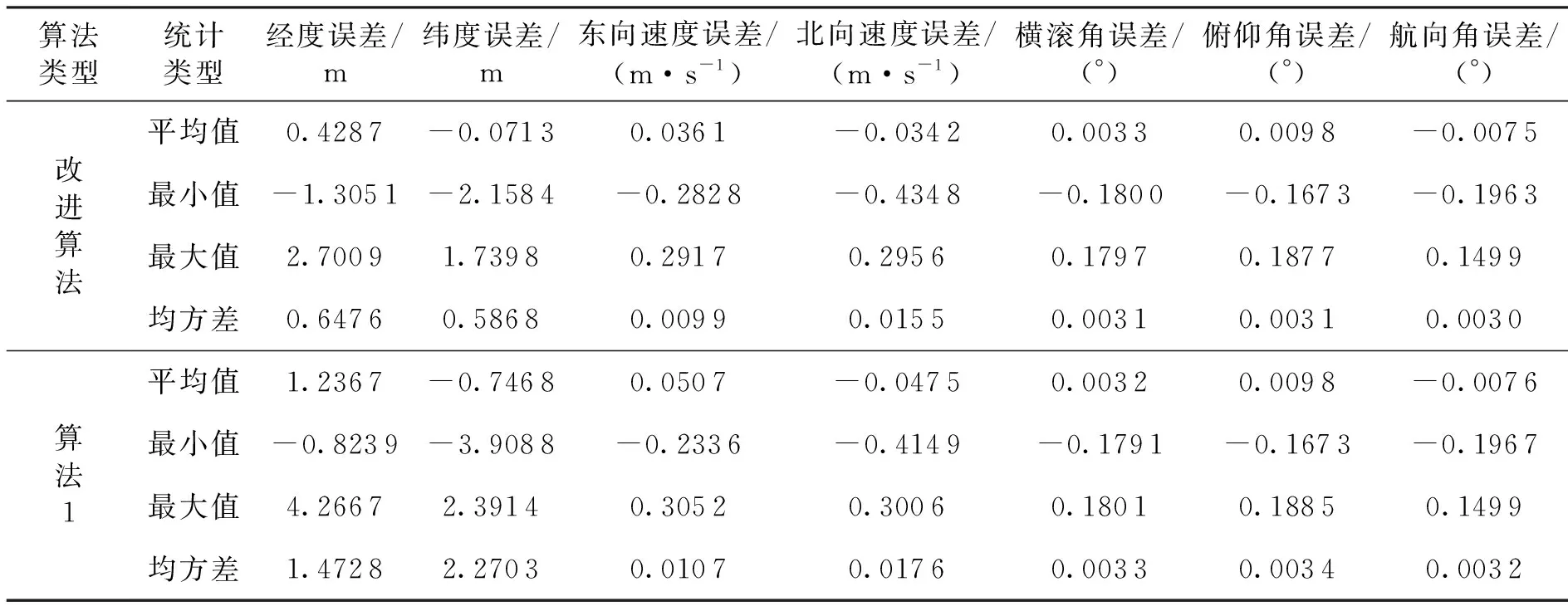
表2 试验结果数据统计对比

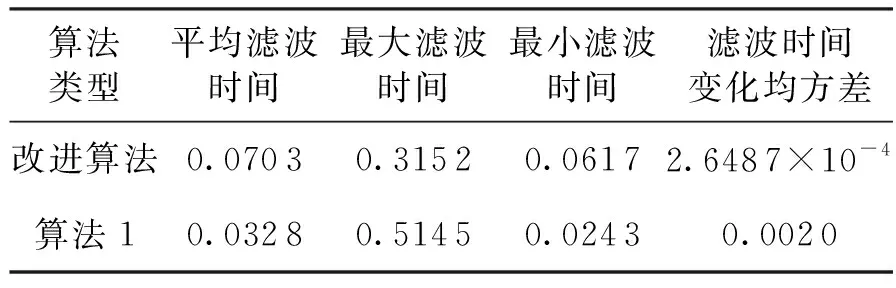
表3 两种算法的计算量对比

2)本文算法的计算量与算法1的计算量在同一个数量级。特别是随着计算机性能的不断提高，该计算量更显得微不足道。

故基于本文改进算法的多传感器组合导航系统不仅滤波精度较高，而且计算量较低。

本文仅对同步的多传感器组合导航系统进行了研究，而实际情况下经常出现的是异步采样多传感器组合导航系统，这也是本文作者日后研究的工作重点。