可重复使用运载器再入轨迹与制导控制方法综述

田栢苓，李智禹，吴思元，宗群

天津大学 电气自动化与信息工程学院，天津 300072

可重复使用运载器(Reusable Launch Vehicle, RLV)是指能够快速穿越大气层、自由往返于地球表面与太空之间的多用途可重复使用飞行器。它既可以快速、便利地向空间运送有效载荷，也可以较长时间在轨停留或机动，完成任务后又可安全、准确地降落在地面。随着空间利用在国家安全和经济社会中作用的日益凸显，航空航天技术高度结合的新一代可重复使用运载器正逐渐成为当今世界军事强国重点关注的战略发展方向，研究与之相关的科学问题具有前瞻性、战略性和带动性。

与传统飞行器不同，RLV的再入返回利用大气层使飞行器在飞行中消耗能量、减速下降，是整个飞行过程中环境最为恶劣，飞行特性最为复杂的阶段。RLV整个再入过程可划分为再入段、终端能量管理段和进场着陆段，如图1所示。在再入返回过程中，飞行器经历了从高超声速到超声速再到亚声速的过渡，导致飞行器在再入过程中呈现出异常复杂的飞行特性，主要体现在以下方面：

1) 耦合特性严重。由于其大空域、宽速域、高机动的飞行特性，RLV轨迹与姿态变化剧烈，飞行器模型除受到非线性特性影响外，亦呈现出强烈的姿轨耦合、横纵交叉耦合及通道耦合特性[1-3]。

2) 不确定程度高。飞行器再入过程气动环境恶劣，飞行器受到大量外界干扰和气动参数不确定的影响，导致飞行器模型表现为强不确定的特性，例如，X-33可重复使用飞行器在俯仰方向上的气动力矩不确定和俯仰方向上的阻尼不确定分别高达43%和80%[4]。

3) 约束条件苛刻。受飞行器自身结构的限制，RLV再入过程必须严格满足热流、动压、过载及可能存在的路径点和禁飞区约束，加之拟平衡滑翔条件(确保飞行器的平稳飞行)的引入，导致RLV的再入飞行走廊被限制在非常狭小的飞行区域[5-7]。

4) 安全面临挑战。为了获得更高的机动性能和操纵性，提高飞行器应对复杂飞行环境的能力，RLV在布局设计时往往采用除传统副翼、方向舵和升降舵以外更多的操纵面，如升降副翼和机身襟翼等。由于飞行环境和自身结构的复杂特性，执行机构的冗余也使得执行器发生潜在故障(如卡死、部分失效和完全失效等)的可能性显著增加，给飞行安全带来巨大挑战。

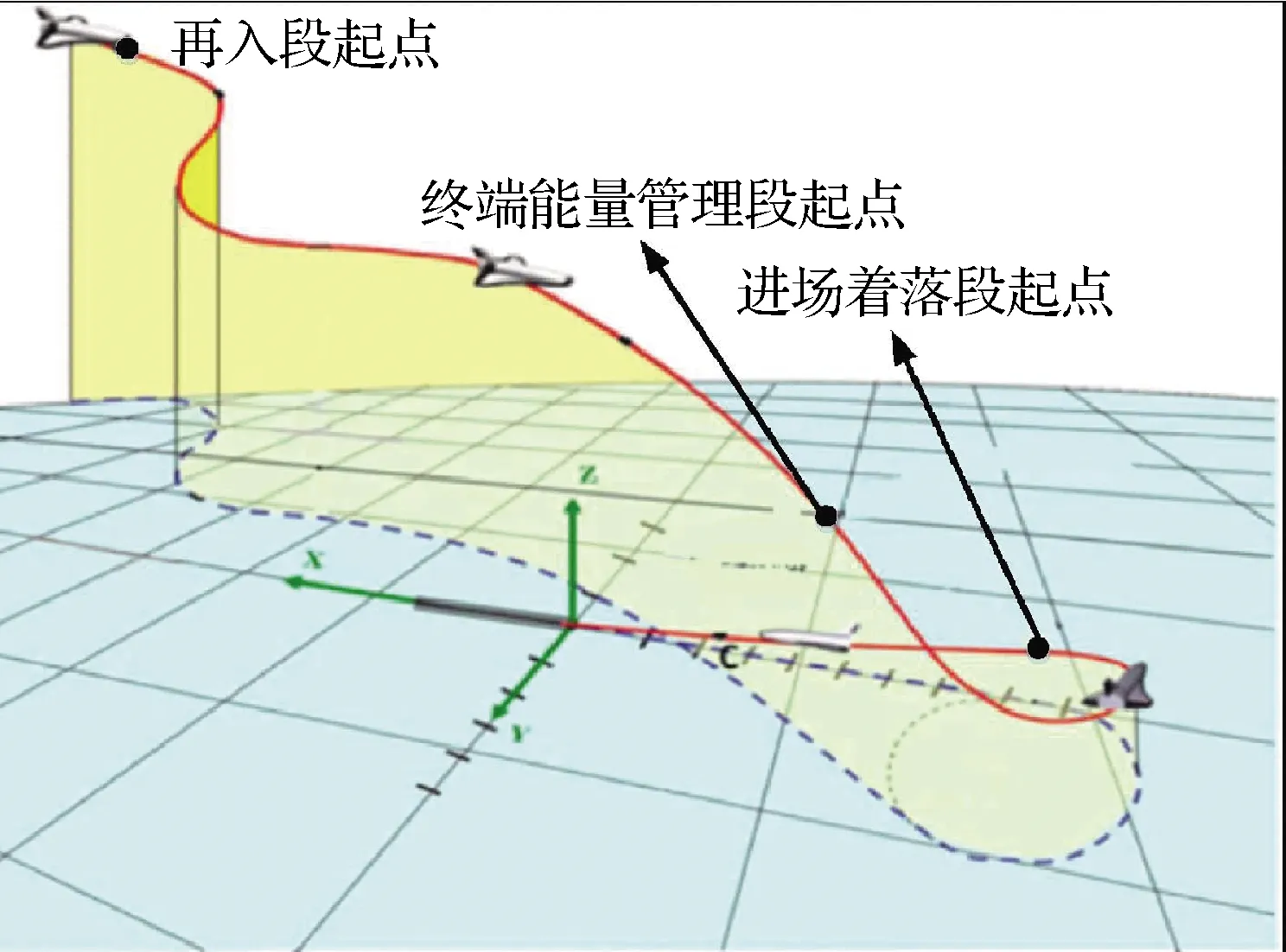
图1 RLV再入飞行示意图Fig.1 RLV reentry flight diagram

综上所述，RLV是一个集多变量、强耦合、非线性、不确定、多约束及潜在执行器故障影响的复杂被控对象，其高自主性、高可靠性、高安全性和高灵活性的制导控制系统设计面临巨大挑战，相关技术的研究已经成为当今航空航天领域最为前沿的研究课题之一。本文系统地对RLV再入段轨迹优化、制导控制及制导控制一体化方法进行了综述性分析，在对每类方法特点深入分析的基础上对其发展趋势进行了展望，研究结果可为从事相关工作的科研工作者提供有益参考。

1 RLV再入轨迹优化方法

1.1 再入轨迹优化问题描述

RLV再入轨迹优化的主要任务是通过优化求解获得满足各种路径约束(动压、热流密度和过载约束)、状态量和控制量及边值约束的可行再入飞行轨迹，并使得某一性能指标优。就其科学问题而言，RLV再入轨迹优化问题是一个复杂的、高度非线性的、多变量、多约束的最优控制问题，对该问题的求解最早可追溯到1696年Johann Bernoulli提出的最速降线问题[8]，航空航天领域对飞行器轨迹优化问题的研究，发展至今已经有60多年的历史，国内外许多学者基于上述理论以及非线性优化理论，在飞行器轨迹优化的求解上进行了大量的研究工作，取得了丰硕的研究成果[9-10]。接下来将按照轨迹优化问题求解的分类方法：间接法、直接法、伪谱法、凸优化方法以及智能优化方法，对RLV的轨迹优化求解方法进行综述。

1.2 间接法

间接法是早期求解飞行器轨迹优化问题的常用方法，该方法基于变分理论和Pontryagin极小值原理，通过引入Hamiltonian函数，来推导最优控制问题的一阶必要条件[11]，最终将飞行器轨迹优化问题的求解，归结为对Hamiltonian边值问题的求解。早期飞行器轨迹优化中常用的间接法为间接打靶法(Indirect Shooting Method)[12]，从20世纪70年代开始，美国密西根大学的Vinh[13-14]，基于间接打靶法开始对高超声速及星际航天器的再入轨迹优化问题进行研究，然而该方法求解时，对初值较为敏感。为了减弱其对初值的高敏感特性，20世纪80年代，间接多重打靶法(Indirect Multiple-Shooting Method)开始逐渐受到重视。近年来，在利用间接法对轨迹优化问题的求解中，更多的关注点放在协态变量的初值估计上，如基于Trim-reference函数的间接法[15-16]，该函数的引入有效地保证了协态变量估计的稳定性，提高了轨迹优化问题求解的快速性。西班牙马德里理工大学的Gomez-Tierno等[17]在获得Hamiltonian边值问题的前提下，利用伴随控制变换(Adjoint-Control Transformation)[18-20]将协态变量的初值映射到一个有界球空间内，并基于对协态变量初值的估计，利用信赖域算法对边值问题进行求解，获得了系统的最优轨迹，该方法体现了较好的实际应用价值。

1.3 直接法

随着计算机技术的不断发展，从20世纪70年代开始，基于非线性规划理论的直接法，由于无需推导最优控制问题的一阶必要条件，因而，在轨迹优化问题的求解中受到了更多的关注。20世纪70年代初，学者Brusch[21-22]和Hull[23]等将直接打靶法引入到最优控制问题的求解中。随后，Dickmanns和Well[24]提出了配点法的思想，该方法相比于直接打靶法能够更好的处理终端时间自由的最优控制问题。20世纪90年代，波音公司的Betts等[25]为了改进多重打靶法计算速度上的缺陷，研究了具有并行计算能力的多重打靶法，并将其应用到轨迹优化问题的求解中。与直接打靶法相比，基于同时离散控制变量和状态变量的配点法，由于对初值不敏感[26]，因此，在飞行器的轨迹优化中得到了更多的应用。随后，Standford的轨道专家Conway等[27]利用直接配点法和非线性规划技术研究了有限推力航天器的轨迹设计问题，文章首先对轨迹优化问题进行离散处理，然后基于序列二次规划(Sequntial Quadratic Programming，SQP)算法对离散后的非线性规划(NLP)问题进行求解，获得最优飞行轨迹。基于直接法的飞行器轨迹优化求解策略中，除了利用SQP算法对离散后NLP问题求解外，内点(Interior Point，IP)法是另一种被经常采用的非线性优化求解方法[28-29]。虽然SQP算法和IP算法是目前求解NLP问题最为有效的2种非线性优化方法，但是由于RLV再入轨迹优化问题自身的复杂性，经过直接配点离散处理的轨迹优化问题是一个大规模的NLP问题。对该问题的求解依赖于对其初值的有效估计，不恰当的初值猜测往往会导致问题的解无法收敛，或是陷入局部极小。

1.4 伪谱法

伪谱法起源于求解流体力学的谱方法[30]。1995年，美国海军研究生院的Banks和Fahroo[31]首次将Legendre伪谱法引入到最优控制问题的求解中，随后，该方法被广泛应用到对最优控制问题的研究中，研究的重点围绕算法的收敛性以及其协态映射定理的等价性证明上[32-39]。由于该方法在求解精度和速度上的优势，已经被广泛应用到航天器的轨迹优化[40-42]和实时制导[43-45]领域。虽然，Legendre伪谱法在理论上和实践上被证明是一种求解复杂飞行器轨迹优化问题的有效方法，但经该方法离散化得到的NLP问题的KKT(Karush-Kuhn-Tucker)条件，与离散的最优控制问题的一阶必要条件之间的等价性，一直没有得到完全证明。2004年，麻省理工的Benson[46]在其博士论文中，针对Legendre伪谱法存在的不足，提出了Gauss伪谱法，并证明了上述等价性在有路径约束的情况下成立。随后，Huntington[47]对方法进行了改进，将上述结论进一步推广，证明了这种等价性在同时存在路径和一般动力学微分方程约束的情况下仍然成立，并对Gauss伪谱法、Legendre伪谱法和Radau伪谱法进行了仿真比较，验证了Gauss伪谱法在求解最优控制问题时往往具有更高的求解精度和更快的收敛速度。上述特点使得Gauss伪谱法成为目前求解复杂最优控制问题最有效的方法之一，该方法在航天器轨迹设计中的应用可参考文献[48-50]。近几年，为了提高飞行器轨迹优化问题的求解速度，改进伪谱法离散点的配置效率，一些自适应伪谱策略开始受到关注，该策略能够根据轨迹自身特性，自主确定轨迹优化求解所需的网格数及离散节点数，有效提高了求解的精度和灵活性[51-54]。

1.5 凸优化方法

与求解NLP问题相比，利用凸优化求解RLV再入轨迹优化问题在求解速度上具有较大的优势，且具备全局收敛性，使得其在RLV 轨迹在线求解上的应用成为可能。2015年，北京航空航天大学的刘新福和爱荷华州立大学的Lu等[55]将凸优化方法中的二阶锥规划方法应用于多约束再入轨迹优化问题，并对其全局收敛性进行了证明，仿真结果表明二阶锥规划方法的求解速度远远快于采用直接配点法的PSOPT软件。然而文章中对飞行速度采用近似化的能量函数进行逼近，轨迹求解的精确性可能因此受到影响。因此，在此基础上，普渡大学的Wang和Grant[56]提出将序列凸规划(Sequential Convex Programming，SCP)方法用于求解带有约束的行星再入轨迹优化问题，该方法具备良好的收敛速度，具有用于实时轨迹规划的潜力。序列凸规划化的主要思想是通过求解序列近似凸子问题，实现子问题的解向原问题的收敛。2019年，Wang和Grant[57]提出了一种基于信赖域更新策略的序列凸规划方法，该算法相较于传统的序列凸规划算法，通过实时对信赖域进行更新，使算法具备提升收敛性能的可能，轨迹求解的实时性得到了进一步的提升。

1.6 特点分析

基于间接法的轨迹优化求解方法具备以下特点：① 基于间接法获得的轨迹具有较高的精度；② 对于复杂的飞行器轨迹优化问题，基于Pontryagin极小值原理推导其一阶必要条件过程非常繁琐，且当问题存在路径约束时，需要事先知道约束弧段的先验信息；③ 问题求解对系统状态和协状态变量的初值非常敏感，最优解的收敛域很小，且协态变量本身毫无物理意义，进一步增加了问题的求解难度。

基于直接法的轨迹优化求解方法具备以下特点：① 不需要推导轨迹优化问题的一阶必要条件，避免了对毫无物理意义的协态变量初值进行猜测；② 与间接法相比，直接法的收敛空间更大，更适合求解复杂的飞行器轨迹优化问题；③ 直接法无法对轨迹优化问题的一阶必要条件进行验证，轨迹的最优性难以保证；④ 直接法离散后的NLP问题的求解依赖于其优化参数的初值，不恰当的初值猜测，将导致NLP问题的解难以收敛或陷入局部最小。

基于伪谱法的轨迹优化求解方法具备以下特点：① 伪谱法既避免了间接法求解轨迹优化问题对协态变量的估计，又通过协态映射定理确保了轨迹求解的最优性；② 能以较少的离散点获得较高的轨迹求解精度； ③ 伪谱法需要认为飞行轨迹要足够光滑，否则伪谱法的谱收敛特性将丧失。

基于凸优化方法的轨迹优化求解方法则具备较快的轨迹求解速度，但是其需要通过近似凸优化问题向原轨迹优化问题逼近，因此轨迹的最优性欠缺。

间接法、直接法、伪谱法以及凸优化方法的求解轨迹优化问题特点的归纳总结如表1所示。

表1 再入轨迹优化方法汇总及特点分析Table 1 Summary and characteristic analysis of reentry trajectory optimization methods

1.7 RLV再入轨迹优化方法发展展望

RLV再入轨迹优化是一个复杂的、高度非线性的、多变量、多约束的最优控制问题。多年来，经过国内外学者的不断努力和大量的工程实践经验，目前满足RLV再入轨迹离线设计的优化算法已相对成熟，并开发了较为成熟的软件工具包，如：GPOPS[58]、OPTY[59]、DIDO[60]、TOMLAB/PROPT[61]等。此外，基于前述方法进行在线轨迹设计的文章也有公开发表，具体可参见文献[62]，目前在线轨迹优化算法主要是前述方法在应用上的推广，轨迹求解实时性往往难以满足RLV高速飞行的要求。随着RLV任务复杂性的不断提高，为了满足新一代RLV自主性(Autonomy)、可靠性(Reliability)、安全性(Safety)和灵活性(Flexibility)的目的，RLV轨迹必须具备在线轨迹快速规划能力。因此，探索收敛速度快，求解精度高，适用范围广的新型轨迹优化算法将成为未来RLV实时再入轨迹优化领域研究的重要方向。

2 RLV再入制导方法

RLV再入制导律设计的主要目的是构建制导指令与飞行轨迹之间的闭环反馈关系，确保在满足再入飞行走廊的前提下，引导RLV从初始再入点向目标点安全过渡，并为姿态控制系统提供可行的再入制导指令[63-64]。20世纪60年代初，再入制导方法开始受到广泛研究，文献[65]对60年代之前的再入制导理论进行了综述。经过30多年的发展，90年代初，国内外研究者进行了大量的再入制导研究工作，再入制导技术取得了突破性的进展。随后，美国的马歇尔航天中心、美国空军实验室和欧洲宇航局相继提出了先进制导控制(Advanced Guidance and Control)[66]、集成自适应制导控制一体化(Integrated Adaptive Guidance & Control)[67]和面向可持续飞行制导控制故障诊断(Advanced Diagnosis for Sustainable Flight Guidance and Control)[68]的研究规划，推动了再入制导技术的进一步发展。从制导策略的角度而言，RLV再入制导可以分为标称轨迹制导和预测校正制导，其中标称轨迹制导又可分为离线标称轨迹制导及在线轨迹重构制导。下面结合国内外的研究发展现状对其分别进行综述，并对RLV再入制导方法进行展望。

2.1 离线标称轨迹制导

标准轨迹制导是一种基于偏差进行控制的再入制导方法，该方法首先在计算机内存入离线计算的再入轨迹参数，当飞行器再入大气层后，由导航系统获得飞行器的实际飞行轨迹参数，并与事先存入计算机的标准轨迹进行对比，获得误差信号。然后基于获得的误差，依据设计的制导方法，获得相应的制导律。标称轨迹制导已经在航天飞机再入返回领域中得到了成功应用，是X-33、X-37等许多再入飞行器的基准方法，在RLV再入制导方法中具有重要的工程应用价值。

2.1.1 离线二维标称轨迹制导

1979 年，离线二维标称轨迹制导方法首先应用于航天飞机的再入返回滑翔段中[69]。该制导方法基于给定的攻角-速度剖面，并将约束条件表示成飞行走廊的形式；在此基础上，通过迭代算法得到倾侧角及倾侧翻转策略。通常，离线二维标称轨迹制导采用纵向制导和横向制导分开设计的原则。纵向制导主要通过对给定的飞行剖面跟踪来实现；而在横向制导中，通过设计横向反转走廊并通过横向反转逻辑进而确定侧倾角的符号，最终实现对RLV纵向和横向轨迹的有效控制。纵向制导常用的飞行剖面包括：阻力加速度-速度(Drag Acceleration-Velocity) 剖面[69]、阻力加速度-能量(Drag Acceleration-Energy) 剖面[70]和动压-高度(Dynamic-Altitude)剖面[71]等；在此基础上，大量的飞行剖面跟踪方法，包括线性反馈制导方法[72-74]、基于预测控制的跟踪制导方法[75-77]和改进的加速度再入制导方法[78-80]被提出并应用于RLV再入制导中。通常上述制导方法从2个方面提升再入制导精度：在纵向制导中，设计攻角在给定的剖面附近进行微调，并通过设计倾侧角大小，实现对预测航程误差的消除。

2.1.2 离线三维标称轨迹制导

考虑到2.1.1节中的二维制导方法存在横向机动上的诸多限制，标称轨迹制导方法逐渐向三维制导发展。文献[81-83]基于标称二维剖面，得到RLV轨迹的长度和曲率并通过迭代过程产生三维剖面，进一步生成制导指令，最终通过RLV再入飞行实验验证了所提出方法的有效性。文献[84] 提出了一种三维约束轨迹生成算法，基于约束条件设计高度-速度剖面，同时考虑侧向运动，解析地计算飞行航迹角和倾侧角。上述制导方法采用给定的攻角剖面，仅依赖于倾斜角的变化来满足横向机动性的要求，限制了实际飞行中飞行器的高机动性能。因此，基于离线最优轨迹的三维标称轨迹制导方法被提出。常见的最优轨迹求解方法在前文中已进行了介绍。对于所求得的三维离线轨迹，文献[85]基于RLV状态量偏差，将再入轨迹跟踪问题转化为线性时变(Linear Time-Varying, LTV)系统的状态调节问题，并根据获得的LTV系统，设计了一种基于滚动时域预测算法的再入制导律。此外，基于线性二次调节器(Linear Quadratic Regulator, LQR)方法对转化后的LTV系统设计制导增益，也是飞行器再入过程中一种常用的制导策略[86]。在此基础上，文献[87]提出了基于间接Legendre伪谱法的RLV再入制导方法，该方法相比于LQR方法，可在线实时计算不同飞行状态下的制导增益，无需事先存储大量的增益预值表。

2.1.3 特点分析

离线二维标称轨迹制导将制导分为横向与纵向分别进行设计，降低了计算复杂度，计算实时性较好。然而，该类制导方法主要依靠侧倾角来进行飞行控制，导致给定飞行剖面往往并不能被精确跟踪，航向角和航程会产生一定程度的偏差。此外，给定二维飞行剖面未考虑RLV的横向机动，不能满足RLV高横向机动任务中的再入制导要求[81]。

基于离线最优轨迹的三维标称轨迹制导方法，可以满足再入飞行轨迹的最优性、高机动性及对最优轨迹的跟踪精度等需求。然而。该类制导方法仅能实现对预先设计的离线轨迹进行跟踪，当RLV面临未知的突发事件时，如飞行器故障或飞行任务变更等，离线轨迹将不再满足再入需求，制导性能往往大幅下降甚至失效。图2给出了2种离线标称轨迹制导方法的特点对比。

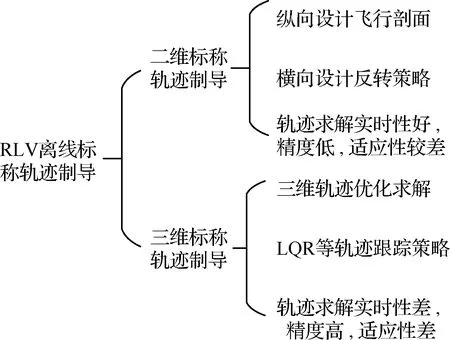
图2 RLV离线标称轨迹制导方法特点Fig.2 Characteristics of RLV off-line nominal trajectory guidance method

2.2 在线轨迹重构制导

2.2.1 在线轨迹重构制导方法

考虑RLV再入过程，当突发事件发生时，离线轨迹不再满足飞行任务需求，需要在线对轨迹进行调整，设计出新的轨迹作为跟踪制导的目标，即在线轨迹重构制导方法。图3给出了在线轨迹重构制导的流程图。文献[62]提出了一种基于在线轨迹优化的实时最优反馈再入制导策略，该方法基于伪谱法，通过连续的实时轨迹优化达到实时闭环最优反馈制导的目的，直至再入过程结束。然而，该方法对系统的实时性带来了巨大的挑战。因此，考虑到凸优化方法的计算效率较高，实时性较好，其在解决航空航天制导问题方面的效用正在迅速提高，并具有机载实时应用的潜力。文献[88] 对凸优化在航空航天中制导方向上的应用进行了综述性研究，并对问题凸化方法及凸化过程的有效性进行了讨论。文献[89]提出了一种基于凸规划的在线轨迹重构制导方法，该方法将非线性轨迹优化问题转变为凸优化问题，进而在每个制导周期内通过求解生成的二阶锥规划问题生成新的参考轨迹，并使用二次规划方法设计最优反馈制导律以跟踪生成的参考轨迹。文献[90]提出了一种基于序列凸规划的在线轨迹重构制导方法，利用序列凸规划方法逼近原非线性轨迹优化问题，并在每个制导周期内对序列凸规划信赖域进行调整，以进一步优化轨迹求解速度。进一步的，文献[91]通过引入指令反解步骤，从而获得原问题在每个离散点处相应的攻角和倾侧角指令。该类凸优化方法虽然在实时性上有所保证，但是系统的最优性能仍有待进一步增强。此外针对RLV再入返回过程中存在禁飞区的问题，文献[92]提出在侧向制导上采用速度方位角误差阈值和人工势场法来减小航向误差并避开禁飞区。文献[93]则提出基于改进的A*算法实现实时轨迹规划过程，并基于考虑禁飞区的飞行器模型，建立了动态优化制导律，使飞行器具备自主避开禁飞区的能力。

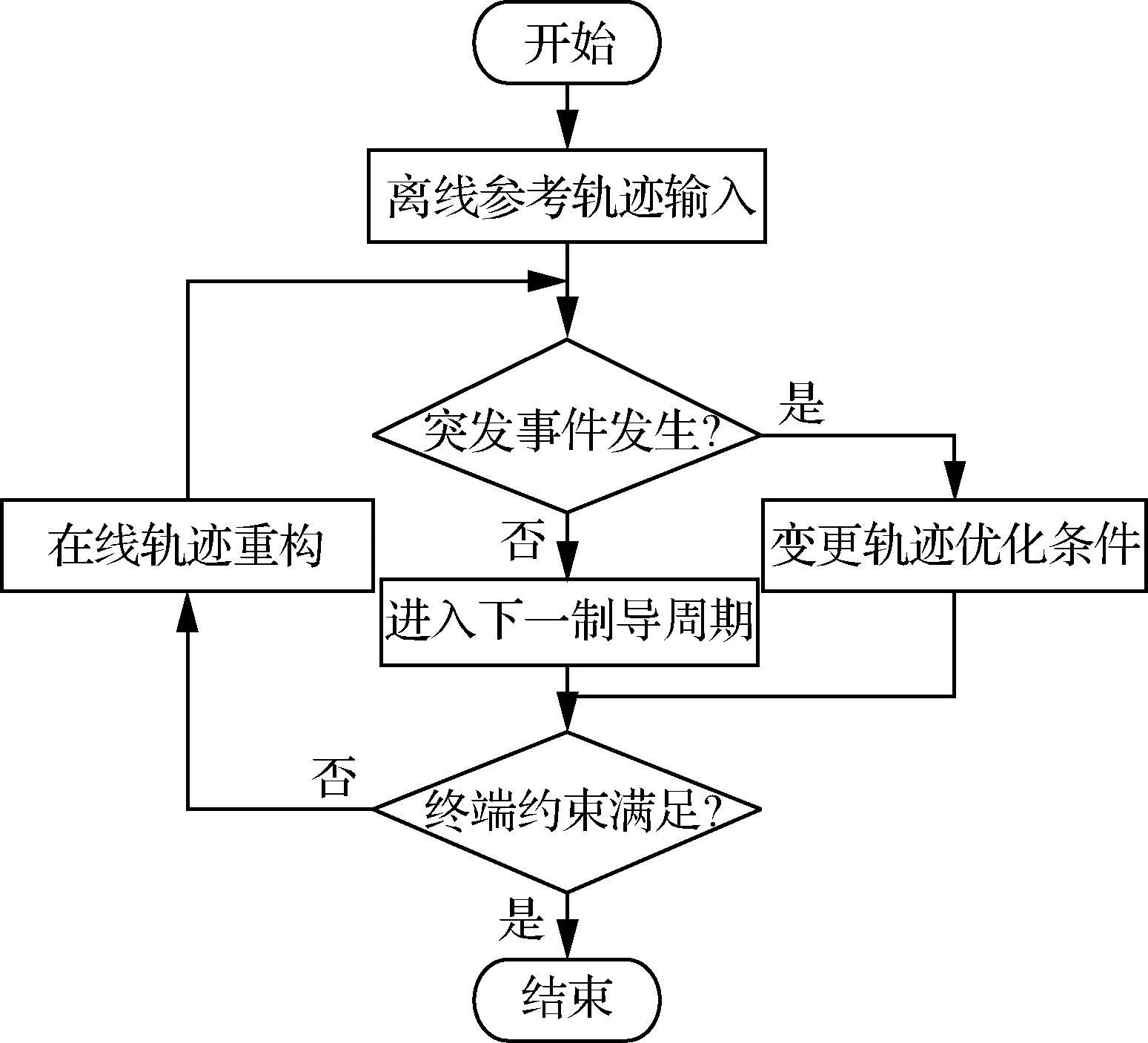
图3 RLV在线轨迹重构制导流程图Fig.3 Flow chart of RLV online trajectory reconstruction guidance

2.2.2 在线轨迹重构制导特点分析

RLV在线轨迹重构制导方法特点总结如下：① 在线轨迹重构制导方法能够根据当前RLV的实际飞行状态快速生成满足所有约束条件的可行飞行轨迹，大大提高了再入制导系统的自适应能力；② 在线轨迹重构制导依赖于在线轨迹求解算法的实时性，若求解最优轨迹过程出现如初值猜测离最优轨迹过远或陷入局部最优解等情况，则轨迹重构实时性难以保证，此时系统的制导性能将下降甚至失效。

2.3 预测校正制导

与标称轨迹制导不同，预测校正制导方法不依赖于参考轨迹，而是在飞行过程中不断对飞行终点进行预测，并根据预测落点与期望终点的偏差来调整控制量。相较于标称轨迹制导，预测校正制导灵活性更好。按照预测方法的不同，预测校正制导可分为解析预测校正制导和数值预测校正制导。解析预测校正制导的基本原理为：通过将轨迹调制到特定形式而获得轨迹的近似解析解，在每一制导周期中对飞行器终端状态进行解析预测，根据预测的终端状态偏差校正控制量。然而由于解析预测计算需要的特有的解析形式以及RLV动力学模型的复杂性，解析预测校正制导方法在求解时往往只能求取近似解析解，预测误差较大，制导精度较低，且参数扰动情况会加剧预测误差，增加了制导控制的难度，因此本文重点对对数值预测校正制导方法进行综述。

2.3.1 数值预测校正制导

数值预测校正制导的基本原理为：通过设定RLV整个再入飞行过程中的控制量参数序列，在飞行过程中不断利用运动方程进行数值积分，以此对终端状态进行预测，并根据预测落点与期望终点的偏差来调整控制参数。图4给出了数值预测校正制导方法流程图。

在预测校正制导方法中，通常设计攻角剖面，而不将攻角作为主要控制量进行设计，即使通过攻角对轨迹进行调整，其调整范围也会受到限制，仅作为控制轨迹的辅助手段[94]。因此，通常将攻角剖面设计为常值[95]，或设计为有关马赫数的函数[96]，此外，攻角剖面的设计还取决于纵向控制和可能的热保护因素[94]。文献[97]基于剩余能量的多少，对攻角剖面进行微调，以增加飞行器的控制能力。文献[98]则考虑航路点约束，使用基于大脑情绪学习的智能控制器实现了对攻角剖面的调整。文献[99]针对低升阻比RLV，提出了一种数值预测校正制导方法，该方法在确定的攻角剖面下，通过设计侧倾角，对动力学方程进行积分得到预测航程，并基于预测航程与期望终点的差值，利用高斯牛顿法迭代更新倾侧角，确保预测轨迹满足终端约束。该文献提出了一种基础的预测校正方法，然而其倾侧角反馈补偿方式、初值设计及校正策略等都尚不完善。为此，文献[100]提出了一种适用于不同RLV的统一预测校正制导方法，该方法引入高度变化率反馈，有效消除了高升阻比RLV再入轨迹的振荡，当需要严格满足轨迹再入约束条件时，高度变化率则基于非线性预测控制方法得到，对预测校正方法的倾侧角反馈补偿方式进行了补充。进一步，文献[101]则针对多约束下的预测校正制导问题，设计了复合走廊，并基于状态预测和反馈理论，设计约束执行算子，通过侧倾角补偿解决再入约束背离问题。文献[102] 采用鸽群启发算法与高斯牛顿法结合的制导方法对倾侧角进行迭代求解，充分结合了鸽群启发算法不需要初值猜测且具备全局收敛性的优点及高斯牛顿法可以在初始猜测的情况下具有高精度全局收敛的优点，为预测校正方法提供了一个合适倾侧角初值设计策略。文献[103]提出了一种基于模糊逻辑的预测校正制导方法，基于模糊逻辑设计调节器，同步校正纵向和横向运动，在一次制导周期内只需进行一次轨迹预测，有效降低了计算负荷，增强了预测校正系统的实时性。文献[96]对目前所提出的数值预测校正制导方法进行了汇总，并从侧倾角剖面设计方法、再入方式选择(跳跃式或直接式)、考虑再入约束的校正方法、无可行解时的解决方法等多个角度对数值预测校正制导进行了改进。最终在NASA Johnson Space Center高保真系统下验证了数值预测校正制导方法的鲁棒性及可行性。文献[95]从横向和纵向两个角度，在实时性上做出了较大的提升。在纵向轨迹控制上，从数值积分的角度提出了改进方法，例如切换Runge-Kutta积分规则、使用自适应积分步长、经验性地减少安全系数等，以节省再入轨迹预测时间；在横向轨迹控制上，不在积分预测期间考虑侧倾角反转，而是设计可变的倾侧角阈值，并使用最终的预测航程来确定何时进行倾侧角反转，以进一步节省轨迹预测时间。文献[104]提出了一种改进的带有混合横向逻辑的预测校正算法，以提高RLV再入过程中的机动性，使RLV具备避开禁飞区的能力。

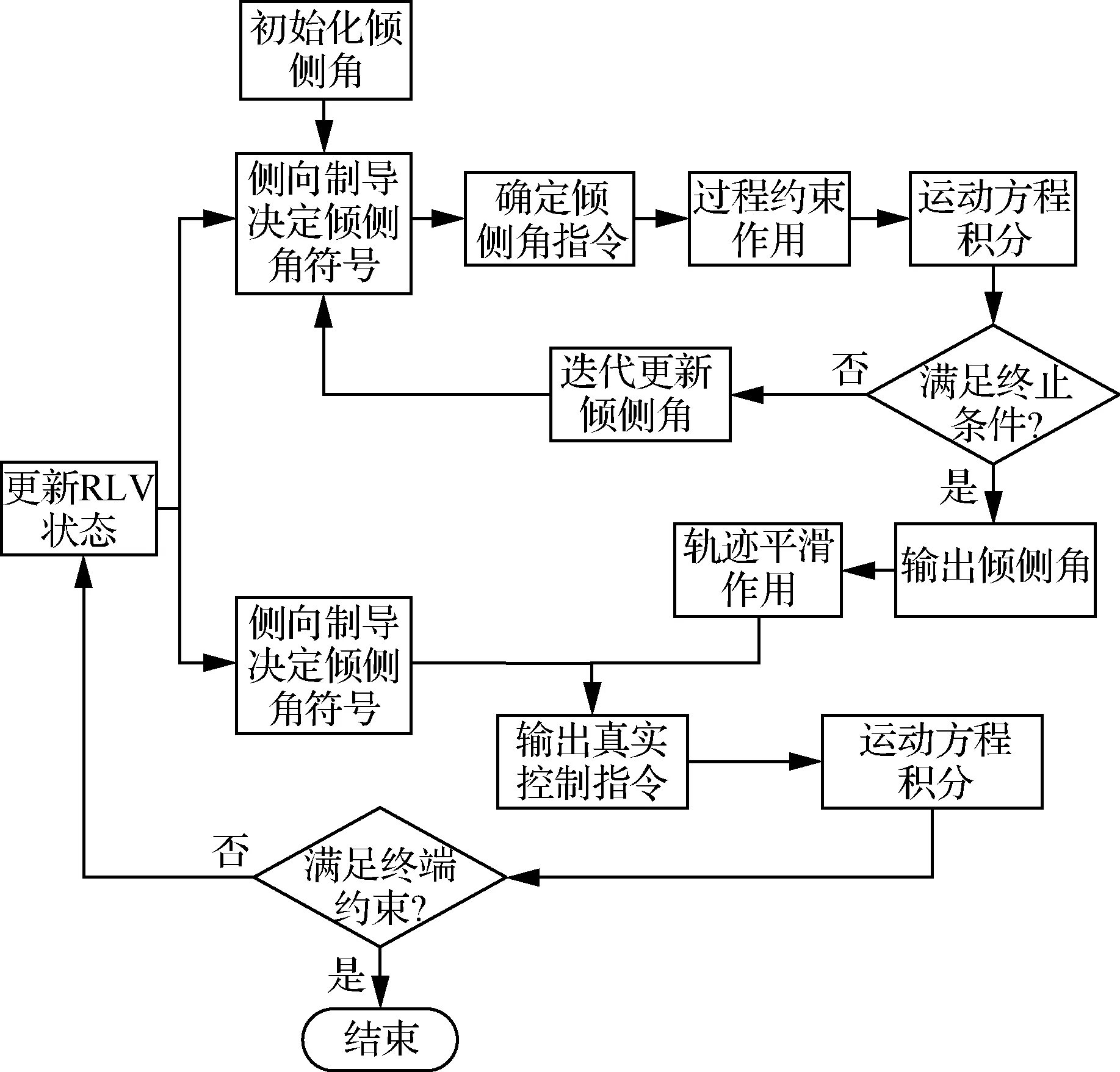
图4 RLV数值预测校正制导方法流程图Fig.4 Flow chart of RLV numerical predictor-corrector guidance method

2.3.2 数值预测校正制导特点分析

RLV数值预测校正制导方法特点总结如下：① 预测校正算法具备灵活性好、不依赖于再入初始状态、自适应能力和鲁棒性强等优点；② 预测校正制导方法往往采用横向制导与纵向制导分开设计的原则，而横向制导中的倾侧角反转策略要求倾侧角瞬间符号翻转，加剧了后续姿态控制系统设计的难度；③ 在侧倾角迭代过程中若某个周期未得到最优解而采用近似最优解，可能导致之后的制导周期内，预测误差无法消除甚至逐渐增大的情况；④ 数值预测校正由于存在着不断数值积分预测与迭代校正的过程，对于机载计算机性能要求很高。

2.4 RLV再入制导方法展望

从制导研究现状来看，采用标称轨迹制导方法对参考轨迹的跟踪，具有计算速度快，易于工程实现等优点，但是存在着对外界扰动适应性低的不足；预测校正制导方法能够处理RLV再入过程中的突发事件，鲁棒性较好，但对机载计算机的运算能力要求较高，实时性较差。两者各有利弊，因此，结合标称轨迹制导与预测校正制导两者优点的混合制导，有望成为未来制导方法发展的主流方向。文献[105]提出了一种LQR方法与数值预测校正方法交替作用的混合制导方法，利用LQR对参考轨迹进行跟踪，并在必要时利用预测校正制导方法对轨迹进行更新，在有效提高制导精度和自适应能力的前提下，显著降低了机载计算机的计算负荷。

从制导策略来看，混合制导方法与在线轨迹重构制导在本质上是类似的，具备较好的鲁棒性与自适应性。该类方法未来的研究方向包括：① 轨迹在线更新算法实时性的改进。不论是自适应伪谱法、凸优化方法还是基于预测校正方法的轨迹规划，考虑到RLV再入过程高速高动态的飞行特性，实时性都略显不足。获得一种实时性好的在线轨迹规划方法，是当前在线轨迹重构制导方法发展的当务之急；② 轨迹在线更新时机的选择。合适的轨迹更新时机选择，不但可以降低机载计算机的负担，减少不必要的计算负担，同时也能更好地提高RLV的鲁棒性。如何合理选择轨迹重构的时机，是未来基于在线轨迹重构制导方法发展过程中需要解决的重要问题；③ RLV最优轨迹与可行轨迹的抉择。在RLV再入离线参考轨迹的设计过程中，通常轨迹设计为使得某一性能指标最优，在线轨迹重构则继承了这一点。而基于预测校正的在线轨迹更新，往往只为求解得到一条可行轨迹。如何在最优轨迹和可行轨迹中进行有效抉择，有效提高轨迹生成的实时性，是未来基于在线轨迹的制导策略中需要重点考虑的问题。④ 基于人工智能技术的制导方法研究，如面向大数据及面向智能规划决策的制导技术等[106]。使RLV具备自主任务规划以及智能决策制导能力。

3 RLV再入姿态控制方法

RLV 再入飞行阶段是整个飞行过程中环境最为恶劣，飞行特性最为复杂的阶段，相比传统飞行器，RLV 模型的耦合特性更严重、气动不确定程度更高，其再入飞行安全面临巨大挑战。因此，RLV再入姿态控制的主要任务是通过设计姿态控制器使系统在受到模型不确定和外部扰动影响的情形下，仍能实现对再入制导指令的快速稳定跟踪控制。接下来，将分别从线性控制、非线性控制及智能控制的角度对RLV再入姿态控制方法进行综述，并对未来RLV姿态控制方法进行展望。

3.1 线性控制方法

线性系统控制理论发展相对比较成熟，基于线性化手段将非线性RLV模型转换为平衡点附件的线性模型, 再基于线性控制方法对转换后的线性系统进行控制器设计，是飞行控制系统设计早期最为常用技术手段。接下来，重点对基于增益调度和线性参变的RLV姿态控制方法进行综述。

3.1.1 增益调度控制

增益调度控制是飞行控制系统设计中经常采用的一种经典控制方法，其核心思想是将非线性模型分解成一系列不同特征点上的线性模型，然后利用成熟的线性控制方法在特征点附近设计一系列的线性控制器，飞行器实际飞行过程中通过参数调度实现不同控制器之间的有效切换。PID控制是目前工程上应用最为广泛的一种控制方法，它的优点在于结构简单、不依赖于被控对象模型、控制所需的信息量少、易于工程实现等。针对X-33飞行器姿态控制问题，文献[107]在参考轨迹附近，基于小扰动理论，结合增益调度，提出了变结构的PID控制方法。文献[108]在不考虑RLV通道间耦合的情况下，以飞行马赫数为调度参数，设计了单通道调度控制器并开发了协调增益调度控制器。文献[109]则通过设计增益调度故障检测和隔离滤波器来实现RLV的姿态控制，并基于H∞理论设计了调度参数，实现了RLV对姿态的稳定跟踪控制。尽管，基于增益调度的控制方法在RLV姿态控制中得到了一定程度的应用，然而，当飞行器在大范围飞行时，为了达到较好的跟踪效果，该方法需要通过计算大量的增益预置表，增加了计算的复杂度，且该控制器往往只能在预设轨迹附近才能有效，当系统不确定和外界干扰较大，导致飞行状态偏离平衡点较大时，往往不能获得理想的跟踪效果。

3.1.2 线性参变控制

基于线性参变控制方法的主要思想是在参数空间内利用所选择调度参数的连续函数表示非线性系统的状态空间矩阵，从而将非线性模型近似成线性参变模型，最后使用线性系统控制方法设计控制器。文献[110]提出了一种基于速度的RLV线性参变模型与控制框架，并与增益调度控制方法结合实现了不确定影响下RLV速度与高度的稳定跟踪控制，然而该方法对系统的计算负担较大。文献[111]提出了一种用于RLV系统的降阶线性参变控制器，该方法基于H∞标准问题，通过对加速度灵敏度函数进行加权以考虑性能指标，将控制问题转换为基于线性变模型表示的控制问题，并使用基于线性矩阵不等式的方法来设计鲁棒静态反馈控制器，对控制器形式进行了简化。进一步，文献[112]考虑再入过程中RLV的强不确定性和耦合特性，使用线性参变方法来设计姿态控制器，通过分析各通道之间的耦合程度，选择线性模型关键参数，实现了线性参变控制器的简化设计，增强了控制器的工程实用性。

3.1.3 线性控制特点分析

上述线性控制方法中，增益调度应用于RLV再入姿态控制时在标称轨迹附件能获得比较好的控制性能，但当RLV的飞行轨迹偏离标称轨迹时，基于增益调度设计的控制器的控制性能将显著降低，此外，为了获得较好的控制性能和提高增益调度方法的适应性，增益调度表需要存储大量的增益值，例如文献[107]为了确保RLV在发动机故障模式下的飞行控制性能，要在增益预值表中事先存储7 800个增益值。除此之外，控制器增益在切换过程中，容易出现参数突变问题，影响控制性能，无法保证闭环增益调度系统的鲁棒性和稳定性[113]。线性参变控制方法设计相对简单，受控系统稳定性和动态性能可以得到有效保证，但是当飞行器的动态特性和扰动特性过于显著时，控制效果较差，飞行器大机动飞行时的鲁棒性有待提高。此外，由于RLV非线性、不确定、强耦合及快时变的特点，当RLV在做大范围机动飞行时，基于线性控制方法设计的控制器，在对RLV进行控制时，往往难以取的很好的闭环控制性能[114]，不同线性控制方法的特点分析见表2。

表2 常用线性RLV再入姿态控制方法汇总及特点分析Table 2 Summary and characteristic analysis of common linear RLV reentry attitude control methods

3.2 非线性控制方法

为了改善RLV控制系统的性能，提高系统的自适应能力，近年来，基于非线性控制的方法在RLV的姿态控制中得到了广泛应用。接下来将重点对基于反步控制、轨迹线性化控制、滑模控制以及预设性能控制的RLV姿态控制方法进行综述。

3.2.1 反步控制

反步控制的主要思想是将非线性系统控制问题分解为若干不超过系统阶次的子系统，再分别设计使得各个子系统稳定的虚拟控制器，然后依次逐步反推控制器和李雅普诺夫函数，最后获得原系统的控制律以实现对系统的全局稳定跟踪控制[115-116]。文献[117]针对非线性系统的有限时间跟踪控制问题，利用辅助控制信号和修正后的误差补偿信号，提出了一种新的有限时间指令滤波反步方法。此外，反步控制与其他控制方法相结合可以更好地提高系统的自适应和鲁棒性，例如滑模控制[118-119]、预设性能控制[120]、鲁棒自适应控制[121]、神经网络控制[122]等。针对不确定影响下的高超声速飞行器的稳定跟踪控制问题，文献[118]基于非线性扰动观测器在线估计非匹配扰动，提出了一种自适应滑模控制器设计方法，实现飞行器对给定参考轨迹的鲁棒跟踪控制。综合考虑外界干扰及输入约束对RLV姿态控制性能的影响，文献[119]将快速终端滑模控制引入反步控制中，提出了一种带约束的自适应反步快速终端滑模控制方案，该方法确保了系统的有限时间收敛，实现了RLV在受限条件下对制导指令的有限时间稳定跟踪控制。文献[120]将反步控制与预设性能控制相结合，提出了一种基于预设性能的RLV姿态控制方法，该方法在确保系统鲁棒性的同时，能够同时保证系统的动态性能和稳态性能。然而，上述文章由于存在虚拟控制输入的重复微分，存在微分爆炸问题。为此，文献[121] 提出了一种鲁棒自适应反步控制方法，方法将虚拟控制输入的时间导数看作不确定的一部分，并利用鲁棒自适应律估计不确定项的上界，从而避免了传统反步中存在的微分爆炸问题。文献[122]研究了一种基于神经网络逼近非仿射模型的反步控制方法，利用神经网络对未知的非仿射动力学模型进行在线估计，通过构造两个基于模型转换的低通滤波器来处理非仿射问题，并将虚拟控制器作为中间变量处理，从而减少反步设计的计算量。文献[123]提出了一种基于辅助误差补偿策略的鲁棒反演控制方法，反步法与神经网络的结合，有效削弱了传统反步法对模型精确性的依赖。

3.2.2 轨迹线性化控制

轨迹线性化控制(Trajectory Linearization Control, TLC)是一种常用的再入姿态控制方法。TLC是20世纪90年代中后期，由俄亥俄大学的Zhu等[124-126]逐步建立并发展起来的一种新型非线性控制方法。该方法可以求得参考轨迹上任意一点的控制增益，通常可理解为一种不需要插值计算的增益调度控制器。且该方法中时变带宽技术的引入，使得控制器能够通过在线调整闭环系统带宽来增强系统的鲁棒性，改善系统的控制性能。文献[127]首次将TLC应用到X-33上升段的姿态控制中。随后，该方法又被应用到X-33飞行器再入段的姿态控制中[128]。进一步，文献[129-130] 在轨迹线性化设计过程中，通过引入改进的时变带宽算法，在实现对姿态控制的同时，提高了系统在执行器饱和及高动压飞行等极限状态下的控制性能。然而，虽然轨迹线性化控制策略能够通过时变带宽技术来增强系统的控制性能改善其鲁棒性，但在实际工程应用中，由于系统自身的限制，闭环系统的带宽不能任意配置，只能限定在一定的范围之内。因此，为了进一步提高系统的鲁棒性，改善其控制性能，近几年学者们从干扰观测器的角度出发，在基于TLC的空天飞行器姿态控制领域做了大量的研究工作。文献[131-133]将干扰观测器和轨迹线性化控制方法相结合，通过设计干扰观测器来估计和补偿不确定对系统性能的影响。然而，上述基于TLC的设计方法中，由于非线性时变反馈调节律的设计理论尚未成熟，导致闭环系统的误差调节器通常基于线性时变系统的状态反馈控制律来实现。这样虽然可以获得沿标称状态的指数稳定，但结果却是局部稳定的。文献[134]中还指出，当控制系统存在较大的不确定时，TLC的控制性能将大幅度降低甚至失效。

3.2.3 滑模控制

滑模控制是一种特殊的非线性控制方法，其区别于其他非线性控制方法之处在于其系统的“结构”是根据系统状态按照期望“滑模动态”的状态轨迹运动。这种滑动模态不仅对系统不确定具有很强的鲁棒性，而且可以通过设计系统的滑动模态使系统获得期望的动态性能[135]。

20世纪90年代末，文献[136-137]针对RLV的姿态控制问题，设计了基于内外环的滑模控制策略，在内环中设计滑模控制器，实现对期望姿态角速率的跟踪，在外环中采用则传统的PI控制器，对外环控制偏差进行校正。此后，文献[138-140]考虑外界干扰、模型不确定、飞行器部分操纵面失效可能导致的执行器饱和对姿态控制性能等的影响，在双环滑模控制结构的基础上，基于时变滑模方法，对RLV姿态跟踪控制问题进行了研究，成功地将滑模控制方法应用到RLV再入姿态控制中。为了提升系统的收敛速度，文献[141]基于多时间尺度特性，将RLV模型划分为快-慢双回路，然后为每个回路设计终端滑模控制器，以确保RLV的稳定飞行。在此基础上，文献[142]基于相同的双回路结构，将终端滑模的二阶动态引入到每个回路，在保证系统快速收敛特性的同时，有效地减弱了系统抖振。文献[143]结合干扰观测器，提出了一种多变量非奇异终端滑模控制策略，首先设计有限时间干扰观测器，以估计模型的不确定和外部干扰，然后基于扰动估计，设计了一种结合了多变量非奇异终端滑模的复合控制器，使姿态跟踪误差在有限时间内收敛到零。进一步，为了优化终端滑模状态收敛速度，文献[144] 提出了一种基于非奇异终端滑模的固定时间RLV再入姿态控制方法，以保证制导指令可以在固定时间内被跟踪，且收敛时间不依赖于RLV的初始状态。进一步，考虑系统部分状态未知对RLV姿态控制性能的影响，文献[145]在输出反馈框架内，基于双极限齐次性理论的设计了固定时间滑模再入姿态观测器-控制器，基于该方法设计的控制策略，在确保对RLV综合干扰及未知状态在线估计的同时，能实现对给定制导指令的高精度快速稳定跟踪控制。此外，考虑RLV外界干扰边界不可知的情况，文献[146]提出了一种结合多变量干扰观测器和模糊快速终端滑模控制的新型有限时间收敛控制方法，该方法实现了模糊逻辑与终端滑模的有效结合，同时可根据外界扰动自适应动态调节逼近律的增益系数，能够有效解决不确定边界未知情形下的RLV稳定跟踪控制问题。

传统滑模控制中的抖振问题一直是影响其实际工程应用的主要障碍，高阶滑模在保持传统滑模控制强鲁棒性的同时，能有效削弱控制抖振，提高系统的跟踪精度。文献[147]针对RLV姿态控制问题，提出了一种基于时变高阶滑模的RLV再入姿态控制策略，通过设计时变滑模面，使系统状态在初始时刻就位于滑模面上，该方法在确保了系统全局鲁棒性的同时，保证了系统在事先给定的时间内对给定制导指令的稳定跟踪。文献[148] 提出了一种基于拟连续高阶滑模的RLV再入姿态控制策略，将控制输入的导数作为虚拟控制进行控制器设计，从而有效地削弱抖振，同时能够保持控制信号的连续性。文献[149]提出了一种基于输入输出线性化和连续高阶滑模的飞行控制器设计策略，通过构建了高度和速度相关的输入输出线性化模型，然后设计基于有限时间的连续高阶滑模控制器。文献[150-151]针对高超声速飞行器的稳定跟踪控问题，提出了一种自适应高阶滑模的控制器设计方法，该方法将自适应策略引入高阶滑模当中，可在外界干扰边界未知的情况下，通过自适应调整控制增益，从而实现对参考指令的稳定跟踪控制。

由于超螺旋滑模控制对模型的匹配不确定具有完全鲁棒性，且能提供绝对连续的控制信号等诸多优点，该方法在RLV的姿态控制系统设计中得到广泛关注[152-153]。文献[62,154]将超螺旋滑模和有限时间干扰观测器结合，提出了一种基于干扰补偿的超螺旋滑模再入姿态控制策略，基于该方法设计的控制策略，在确保对外界干扰在线观测的同时，可实现对给定制导指令的快速稳定跟踪。文献[155]考虑RLV再入过程中乘性力矩扰动影响且模型不确定及扰动上界均未知的情况，基于内-外双环控制结构，设计了一种增益自适应的多变量超螺旋滑模控制器，该方法能够确保控制器增益非过估计的同时，实现了跟踪误差的有限时间收敛。文献[156]提出了一种基于固定时间多变量超螺旋滑模的RLV再入姿态控制器设计方法，设计了具有固定收敛特性的超螺旋滑模干扰观测器和控制器，以确保姿态角跟踪误差在固定时间内收敛到零。

3.2.4 预设性能控制

传统的非线性RLV姿态控制方法虽然能较好地保证飞行器姿态控制的稳定性和鲁棒性，但往往忽略了RLV姿态控制系统的动态品质。随着飞行器对控制精度和控制品质要求的不断提升，近年来，预设性能控制在RLV姿态控制领域得到了广泛关注，其核心思想是对受控系统的状态人为设定性能包络线，通过性能包络函数的收敛特性来刻画受控系统的动态和稳态性能[157]；其内容包括：最大超调小于一个足够小的预先设定的常数、收敛速度不小于一个预先的指定值，跟踪误差收敛到任意小的残差集。预设性能控制方法在控制系统的动态性和稳态性上均表现出了良好的性能优势[158]。预设性能控制方法并没有固定的控制器设计形式，往往可以与其他控制，如滑模控制[159]、反步控制[160-162]等方法的结合来设计相应的预设性能控制器。

文献[159]将预设性能控制方法与终端滑模控制相结合，利用切线函数提出了一种具有预设性能的自适应抗饱和终端滑模控制策略，解决了RLV在外界干扰、输入饱和、模型参数不确定等综合影响下的姿态跟踪控制问题。文献[160]针对不确定影响下，严格反馈非线性系统的有限时间跟踪控制问题，提出了有限时间性能函数的概念，并综合利用预设性能技术和反步方法设计了状态反馈控制器，该方法能够保证系统跟踪误差在有限时间内满足期望的动态和稳态性能。文献[161] 基于反步控制方法，在反步设计的每一步中，构造预设性能函数使飞行器的跟踪误差在规定的边界内，在此基础上保证了速度和高度控制子系统所需的动态性能和稳态性能。文献[162]在执行器故障和空气动力学不确定情况下，研究了飞行器预设性能稳定跟踪控制问题，分别为速度和高度子系统设计动态反步控制器和鲁棒自适应反步控制器，解决了执行器故障情况下，以跟踪误差动态性能约束为特征的稳定跟踪控制问题。

3.2.5 非线性控制特点分析

在上述非线性控制方法中，反步控制方法对飞行器控制系统中存在的非匹配不确定有着良好的抑制能力。然而，反步控制由于存在虚拟控制输入的重复微分，容易出现“微分爆炸”问题，从而增加了RLV控制系统设计的复杂性。轨迹线性化控制方法是一种基于微分代数谱理论的非线性控制方法，在NASA先进制导控制项目中被成功应用于X-33的上升段姿控系统设计中，该方法不依赖于参考轨迹，参数调整简单，易于工程实现，但只能获得沿标称状态的指数稳定。滑模控制方法具有收敛速度快、对参数变化及外部扰动不敏感、无需系统在线辨识参数等优点，众多形式的滑模控制方法为RLV再入姿态控制问题带来了多种解决途径，但滑模控制中的抖振无法完全消除，只能在一定程度上削弱，且随时有可能激发被控对象未建模动态的风险。预设性能控制在控制器设计过程中，同时兼顾了系统的动态性能和稳态性能，控制精度往往可事先设定，预设性能控制方法没有限制控制器的具体设计形式，通常与其他形式的控制器混合使用。不同控制方法的特点分析见表3。

表3 常用非线性再入姿态控制方法汇总及特点分析Table 3 Summary and characteristic analysis of common nonlinear RLV reentry attitude control methods

3.3 智能控制

随着计算机性能及智能控制的发展，智能控制方法逐渐开始被应用于RLV再入姿态控制当中。目前智能控制在RLV上的应用主要包括模糊控制以及神经网络控制，接下来分别对其进行综述。

3.3.1 模糊控制

模糊控制因其对模型不确定和未建模动态的良好逼近特性被应用于RLV的姿态控制系统设计中。文献[163]提出了一种基于可调结构的自适应模糊滑模控制RLV姿态控制器设计方法，其中引入可调结构主要目的是为设计隶属函数使其包含模糊输入的所有变化，并设计了与航迹角相关的滑模面，通过引入高度和速度的误差以提高控制性能，最终结合可调结构和滑模控制方法，设计了可以针对姿态跟踪误差的变化进行灵活调整的模糊控制器。进一步，考虑执行器故障对RLV姿态控制性能的影响，文献[164]基于Takagi-Sugeno(T-S)模糊模型，研究了执行器故障下的RLV姿态容错控制问题。文献[165-168]针对RLV自适应模糊姿态控制问题展开了相关研究，在确保系统稳定的前提下，提高了姿态跟踪系统的抗干扰能力。其中，文献[165]将模糊逻辑系统与自适应技术相结合，设计了一种基于自适应模糊控制策略的姿态跟踪控制器，对系统不确定进行在线估计及补偿，并在控制策略中引入了补偿控制器，该方法可以有效减小模糊建模误差对控制性能和系统稳定性的不利影响。文献[166]采用复合自适应模糊H∞控制策略，研究了参数不确定和外部干扰条件下RLV再入姿态控制问题，该策略采用自适应模糊H∞控制方法结合辨识模型设计姿态跟踪控制器，有效提高了在模糊逼近区域内，系统的跟踪性能。为了进一步提高系统的抗干扰能力，文献[169]研究了一种基于扰动观测器的混合H2-H∞鲁棒模糊跟踪控制策略，该方法通过实时在线补偿综合干扰，实现了对飞行控制抗干扰能力的提升。文献[170]提出了一种基于模糊扰动观测器的自适应滑模控制方法，在建立考虑综合扰动的气动弹性模型的基础上，利用模糊估计误差和观测误差进行扰动估计，构造了一种基于模糊逻辑系统的扰动观测器，并结合自适应滑模控制算法，有效提高了再入姿态的鲁棒跟踪控制能力。

3.3.2 神经网络控制

神经网络控制是20世纪80年代末期发展起来的控制方法，该方法为解决复杂的非线性、不确定系统的控制问题开辟了新思路。文献[171]设计了RLV离散时间自适应神经网络控制器，基于一阶泰勒展开得到离散时间模型，并设计了基于标称反馈和神经网络逼近的虚拟控制器，该方法具备较好的自适应性和自学习能力，可以有效提高系统的抗干扰能力。文献[172]提出了一种针对飞行器纵向模型的非奇异神经网络控制系统设计方法，对于速度子系统，直接设计神经网络控制器，对于转换为严反馈形式的高度子系统，则使用两层神经网络和反步控制策略进行高度控制器的设计。文献[173]在考虑推力和俯仰力矩之间耦合关系的前提下，提出了一种基于反演控制和奇异摄动系统方法的控制策略，并采用RBF神经网络对未知的RLV动力学模型进行逼近，由于RBF神经网络良好的逼近性能，有效提高了系统对外界干扰的抑制能力。文献[174]针对一类具有随机不确定和全状态约束影响下的姿态跟踪控制问题，提出了一种基于RBF神经网络的非过估计自适应控制策略，并上设计了基于神经网络的自适应飞行控制器，该方法通过神经网络逼近器对系统非线性未知项进行在线估计与补偿，有效解决了飞行器在随机不确定和全状态约束下的稳定跟踪控制问题。文献[175]将具有学习功能的神经网络动态面控制与非线性扰动观测器相结合，解决了飞行器在不确定和时变扰动影响下的稳定跟踪控制问题。文献[176]提出了轨迹规划和姿态控制的协同框架，并设计了非敏感的轨迹优化和基于深度神经网络的姿态控制的双层结构。其中，上层负责生成包含最优轨迹与最优控制的数据集，下层控制系统中，基于预生成的数据集，构建深度神经网络并对其进行训练，然后，基于训练完成的深度神经网络，在线生成最优反馈指令，并通过六自由度的仿真验证对算法的实时性及可靠性进行了验证。

3.3.3 智能控制特点分析

模糊控制不需要被控对象的精确数学模型即可实现较好的控制，利用模糊控制系统设计的逼近器能对飞行器的综合干扰进行实时估计与补偿，起到了类似干扰观测器的作用。相较于传统的干扰观测器，基于模糊控制系统设计的逼近器，可基于隶属度函数进行灵活调节，往往具备对干扰更好的估计能力。然而，模糊控制的跟踪效果会因隶属度函数选择而不同，因此在调控的时候的需进行多次试凑。此外，若模糊控制选择不佳，会产生一个模糊系统跟踪误差，进而影响飞行器的跟踪性能。神经网络控制由于其强大的自适应性和自学习能力，可对RLV未建模动态和综合干扰进行很好的逼近，有效提高系统的抗干扰能力。然而，由于神经网络控制系统不能很好的解释自身推理过程和推理依据的逻辑，因此在训练可用于RLV控制的神经网络系统是比较耗时的。此外，不同类型的神经网络系统具有不同的跟踪精度和网络结构复杂度，例如RBF神经网络与BP神经网络，前者的逼近精度要高于后者，但后者的网络结构复杂度相对低。因此，对RLV飞行控制系统进行设计时，高逼近精度的神经网络系统往往会带来飞行控制器更大的复杂度，从而降低了RLV系统的计算效率[177]。模糊控制和神经网络控制特点汇总见表4。

表4 常用智能再入姿态控制方法汇总及特点分析Table 4 Summary and characteristic analysis of common intelligent RLV reentry attitude control methods

3.3 RLV再入姿态控制方法展望

基于上述对RLV控制研究现状的分析，对未来RLV姿态控制的发展趋势进行展望：① RLV 大空域、宽速域及高机动的飞行特性，使得RLV自身模型的耦合程度、未建模动态及外界干扰在不同飞行状态下差异明显，如何设计抗扰能力强、适用范围广、控制形式及参数调整简单的新型控制算法，是RLV姿态控制领域需要重点关注的研究方向；② 近年来，国内外学者针对基于干扰观测器的RLV扰动补偿控制开展了大量研究工作，并取得了丰富的研究成果，如TLC干扰观测器[131-133]、滑模干扰观测器[145-146]、模糊控制干扰观测器[169-170]等。该方法通过设计干扰观测器在完成对模型不确定及外界干扰在线观测的同时，可实现对给定制导指令的鲁棒跟踪控制，显著增强系统的抗干扰能力[178-179]。鉴于基于干扰补偿控制方法在抑制模型不确定及外界干扰上的显著优势，基于该方法的RLV姿态控制研究将是未来RLV姿态控制领域的重要研究方向之一；③ RLV的轨迹跟踪效果直接受到内环姿态控制性能的影响，为了确保轨迹跟踪的高效性，在满足执行器物理约束的前提下，需要尽可能的提高姿态跟踪的收敛速度，尽管目前已有固定时间控制文献公开发表[156]，但其设计形式较为复杂，难以在实际系统进行应用，如何设计更为简洁实用的具有固定时间收敛特性的飞行控制算法，是未来RLV姿态控制领域需要重点研究的课题。

4 制导控制一体化设计

4.1 制导控制一体化方法

制导控制一体化(Integrated guidance and control, IGC)设计在20世纪80年代被提出[180-181]，旨在将制导系统与控制系统视为一个整体系统，然后直接针对这个整体系统的模型进行制导控制算法的设计，提高制导系统与控制系统的协调匹配程度, 进而改善飞行器的控制品质[182]。当前主要的IGC设计思路为：建立包含制导与控制的六自由度耦合模型，采用小增益控制[183]、反步控制[184]、动态面控制[185]和全状态反馈[186]等完成高阶非线性模型的控制器设计[187]。文献[188]提出了一种考虑输入饱和约束的制导控制一体化设计方法，基于干扰观测器对系统不确定性进行补偿,然后结合加幂积分方法与嵌套饱和方法对控制律进行了设计。文献[189]通过降阶处理，得到飞行器制导控制系统低阶解析模型，将IGC问题转化为低阶非线性系统进行求解，为解决IGC问题提供了新思路。然而，该方法依赖于解析模型的精度，实际过程中往往难以实现。文献[190]通过建立包含质心运动方程和绕质心姿态控制方程的全耦合IGC高阶非线性模型，在此基础上，基于反步控制设计控制器完成姿态控制任务。为了避免反步控制中的微分爆炸，文献[191]利用动态面控制(Dynamic Surface Control, DSC)技术对IGC系统进行设计。此外，滑模控制方法[192-193]和自适应控制方法[194-198]在IGC系统中的应用也得到了广泛的研究。在IGC系统中，考虑模型不确定和外界干扰对系统性能的影响，往往可以通过引入干扰观测器[199]、扩展状态观测器(Extended State Observer, ESO)[200]、神经网络[201]等方法来提高系统的抗干扰能力。例如，文献[200]中利用ESO估计反步控制每个循环中存在的不确定和干扰，以减少IGC系统对模型精度的依赖。

4.2 制导控制一体化方法展望

目前IGC的研究主要还是采用一种分环递推的设计形式，而没有真正意义上将RLV六自由度模型统一到一个环里进行设计，文献[202]指出这种人为分环的设计方式将有可能对RLV安全可达区域的计算产生影响，导致飞行安全隐患。文献[203]提出了一种直接针对RLV六自由度运模型进行轨迹优化的方法，通过该方法能够直接获得飞行轨迹和执行器之间的映射关系，避免了对制导控制系统的分环设计，但这种方法对机载计算机的计算能力要求非常高。基于类似的思路，文献[202]将RLV六自由度模型放在一个环进行设计，基于伪谱法对RLV再入末端的六自由度实时轨迹优化问题进行研究，通过实时轨迹规划直接获得了RLV舵面与飞行轨迹之间的关系，且系统表现出很好抗干扰能力。这种单环的设计思路，近年来也出现在基于强化学习的着陆飞行器制导控制系统设计中，例如文献[204]提出了一种基于强化学习的IGC算法，使用强化学习方法将系统的状态直接映射到执行器层面。文献[205] 则基于深度强化学习理论，直接建立了飞行器轨迹与引擎推力间的映射关系，实现了单环框架下的集成制导控制一体化设计。这种设计思路为单环的RLV制导控制一体化设计提供了很好的借鉴。随着计算机和人工智能技术的不断发展，从提高RLV飞行安全的角度考虑，将RLV的六自由度模型在单环的框架内进行IGC设计具有重要的研究意义，是未来RLV制导控制一体化设计需要重点关注的研究方向。

5 结 语

航空航天技术高度结合的RLV在维护国家安全、应对潜在空间冲突、获取太空战略资源等方面具有极其重要的战略地位，正成为各个军事强国重点关注的研究方向。本文在深入分析RLV再入飞行特性的基础上，较为系统地从RLV再入轨迹优化、再入制导、再入姿态控制及制导控制一体化角度对当前已有的研究工作进行了综述，基于对每类方法深入分析的基础上，对其未来发展趋势进行了展望。希望本文的研究工作可对从事相关研究的科技工作者提供有益参考。