基于误差相似性的移动机器人定位误差补偿
2020-12-01石章虎何晓煦曾德标雷沛
石章虎,何晓煦,曾德标,雷沛
1. 南京航空航天大学 机电学院,南京 210016 2. 航空工业成都飞机工业(集团)有限责任公司,成都 610092 3. 四川省航空智能制造装备工程技术研究中心,成都 610092
随着工业4.0的高速发展和智能制造的快速推进,以工业机器人为载体的飞机柔性化自动装配技术受到广泛关注[1],其中,AGV(Automated Guided Vehicle)式移动制孔机器人因能更好地适应飞机产品大尺寸、多品种、小批量的特点[2]而成为研究热点。工业机器人本身具有较低的绝对定位精度,同时,承载机器人的AGV存在弹性变形,这种弹性变形与机器人位姿直接相关,同时还受到机器人运动速度、运动路径、运动学姿态、负载变形[3]和惯性等的影响,因此会在机器人安装机座处引入较大误差,当表征到机器人末端时,经过了机器人各连杆的传递,会被进一步放大。导致系统绝对定位精度远远不能满足在离线编程工作方式下的飞机自动化装配系统的精度要求[4]。因此,研究精度补偿技术提高系统绝对定位精度是将AGV式移动制孔机器人广泛应用于面向航空制造的柔性化自动装配的关键[5-6]。
传统的精度补偿技术如机器人运动学标定[7],是基于机器人运动学参数的误差模型,利用有限的定位误差采样数据,通过优化算法识别出机器人各连杆的运动学参数误差[8],其中迭代的最小二乘法(Levenberg-Marquardt, L-M)被广泛应用[9]。但该误差模型仅包含机器人几何误差源,当需要包含更多误差源时,势必需要在其中增加更多误差参数,对于AGV式移动制孔机器人,要用数学模型表征出AGV弹性变形的变化非常困难,而且会导致计算复杂程度和计算量大幅提高。
鉴于运动学参数标定方法的缺陷,很多学者探索了其他一些精度补偿方法来提高机器人的绝对定位精度[10-12]。Zeng等[13-14]利用机器人定位误差的相似性建立了机器人定位误差与关节转角之间的空间映射模型,然后对待补偿点进行线性无偏最优估计。该方法仅关注末端定位误差与关节角输入之间的关系,不关注具体误差源,在一定程度上具有很强的通用性。然而该方法在AGV式移动制孔机器人中却有一定的局限性,这种局限性表现在,当AGV弹性变形引起的末端定位误差增大到一定程度以后,这种依赖机器人关节角的映射模型可能难以建立。
其他一些提高机器人定位精度的方法,如在线误差补偿[15-16]需要在末端加装一个实时反馈装置来调整机器人位姿,通常能获得较高的补偿精度,但加装装置对于一些复杂场景不易操作,且相对于离线标定技术造价也更加高昂。因此,在机器人应用的多形式和快速发展背景下,迫切需要对机器人精度补偿技术进行创新。借鉴周炜等[17-18]提出的基于反距离加权法的机器人定位误差补偿方法,利用定位误差的相似性,将AGV式移动制孔机器人整体视作一个“黑箱”,仅关心末端位置输入和定位误差输出之间的关系,用已知的相似点定位误差实现对待补偿点定位误差的估计。
利用定位误差的空间相似性,论述一种适用于AGV式移动制孔机器人的基于反距离加权的空间插值与补偿方法,并通过提出的AGV式移动制孔机器人机座坐标系换站方法,使精度补偿站位的采样点数据通用于其他加工站位。对AGV搭载的KUKA KR480型工业机器人制孔系统进行试验验证,通过试验选取最优网格步长,补偿结果表明该方法能补偿AGV弹性变形对于机器人末端定位误差的影响,较好地提高AGV式移动制孔机器人的绝对定位精度。
1 AGV式移动制孔机器人系统
1.1 系统工作流程
AGV式移动制孔机器人系统如图1所示,系统工作流程如图2所示。

图1 AGV式移动制孔机器人Fig.1 AGV based mobile drilling robot
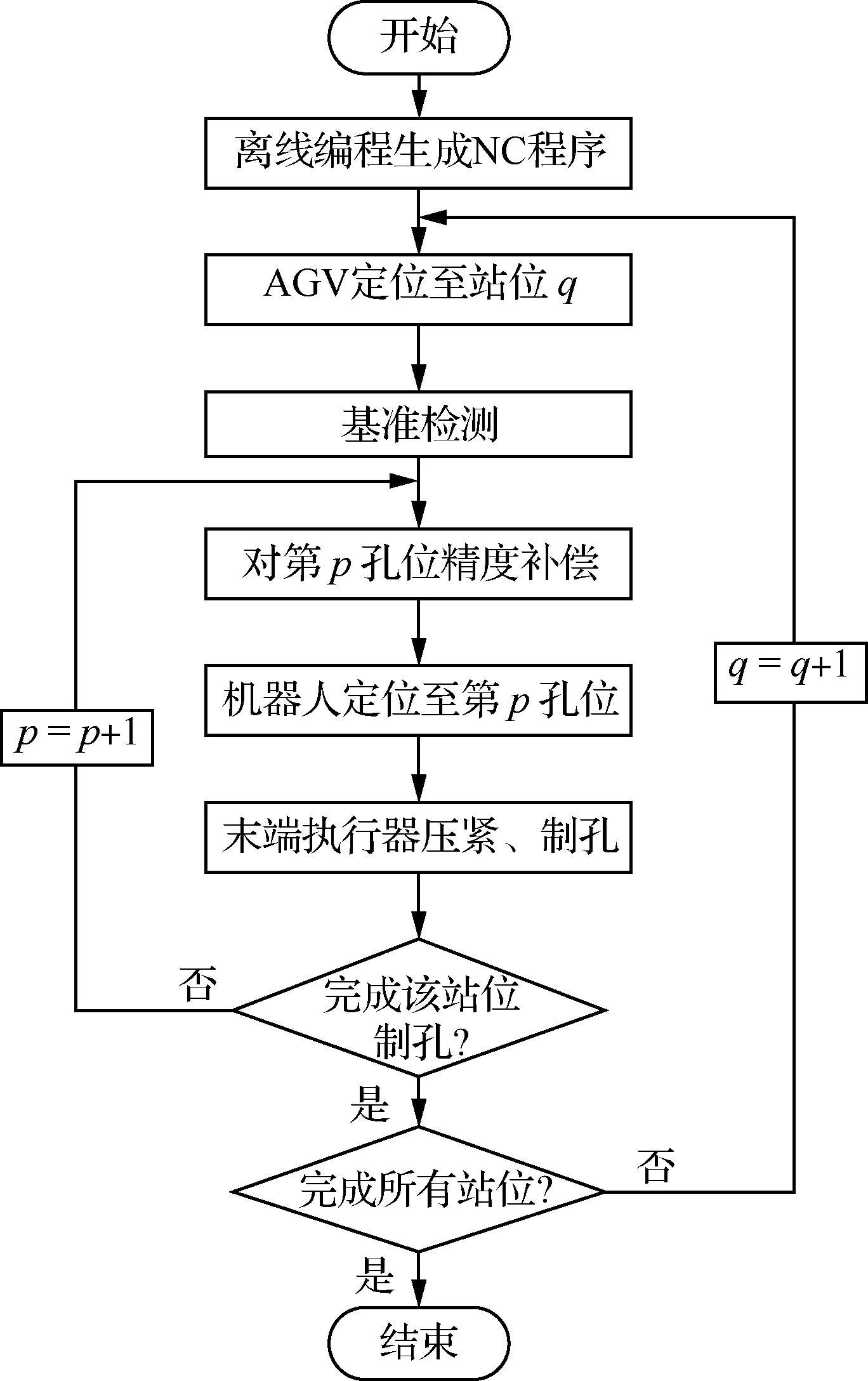
图2 系统工作流程Fig.2 System workflow
系统硬件部分主要由KUKA KR480型工业机器人、AGV、多功能末端执行器以及其他辅助设备组成,系统软件部分主要分为离线编程软件和集成控制软件,本文的精度补偿算法集成在集成控制软件中。系统工作流程如下:首先离线编程软件生成可供集成控制软件解析的NC程序,然后集成控制软件控制AGV定位至待加工站位并进行基准检测,接着对待加工孔位进行精度补偿,机器人到位后末端执行器进行压紧、制孔,循环直至完成所有加工任务。
1.2 系统定位误差
为了观测AGV弹性变形程度以及机器人末端定位误差,将测量杆安装在末端执行器电主轴上,另一端安装靶球座以固定激光跟踪仪的靶球(图1中靶球1);在机器人底座处固定了一个靶标座,固定靶球(图1中靶球2)作为AGV变形的观测点,在机器人默认的HOME位置时,测量观测点的三维坐标为(383.236, -287.460, 63.901) mm,本文中的坐标值均以机器人机座坐标系为基准。KUKA工业机器人规定机座坐标系原点位于底座中心,x方向指向机器人正方向,z轴竖直向上,y轴由右手法则确定,机座坐标系确定了机器人的具体位置和姿态。
在系统实际工程应用的工作空间随机选取了478个采样点,采样点在x,y,z方向取值范围如表1所示。将采样点理论值作为输入,以10%倍率的速度驱动机器人运动,用激光跟踪仪分别测量末端定位误差和观测点三维坐标,数据统计如表1所示,绘制观测点三维坐标的离差折线图如图3所示。
从表1可以看出,由于采样点在y方向取值范围较大,因此AGV弹性变形造成观测点在y方向的离差范围也较大,为[-0.131, 0.127] mm。观测点综合离差达到了0.147 mm。而工业机器人自动制孔系统绝对定位精度要求为±0.5 mm[19],如果仅对机器人做标定,即使只考虑底座处产生的误差向量平移到末端产生的影响,也会使标定的结果大打折扣,因此必须对AGV产生的弹性变形进行补偿。

表1 采样点和观测点数据统计Table 1 Statistical data of sampling point and observation point

图3 观测点离差折线图Fig.3 Deviation line chart of observation point
1.3 系统坐标系换站
在对AGV式移动制孔机器人进行离线编程路径规划时,提取的孔位设计信息是相对于产品坐标系的,产品坐标系在飞机产品建模时创建;同时,在工装设计过程中给定了基准工具球点(Tooling Ball, TB),因此可以通过激光跟踪仪测量工装上TB点的实际三维坐标,结合理论位置坐标,通过奇异值分解法(Singular Value Decomposition, SVD)[20]拟合出产品坐标系。
为了避免精度补偿试验时机器人与产品之间发生干涉,通常会避免在实际工作站位进行精度补偿试验,因此精度补偿站位与加工站位可能不一致;另外由于飞机产品具有小品种、多批量的特点,AGV式移动制孔机器人在使用中存在由于产品变更而导致加工站位具体位置发生改变的可能;同时,离线编程生成的NC程序中的待加工孔位是相对于产品坐标系的,而机器人加工程序和精度补偿采样点数据的参考坐标系为机器人机座坐标系,因此,需将离线编程中待加工孔相对于产品坐标系的坐标值,变换为相对于实际加工站位中机器人机座坐标系的坐标值。通过测量AGV上的靶球座并建立AGV坐标系,利用机座坐标系与AGV坐标系之间的固定变换关系,可对机器人机座坐标系进行重建,从而实现加工孔位坐标信息转换。
图4和图5展现了AGV处于精度补偿站位和当前加工站位时,系统中的坐标系和坐标系之间的空间变换关系。
对于NC程序中给定的加工孔相对于产品坐标系的位姿pThole,相对于当前加工站位中机器人机座坐标系的位姿b2Thole:
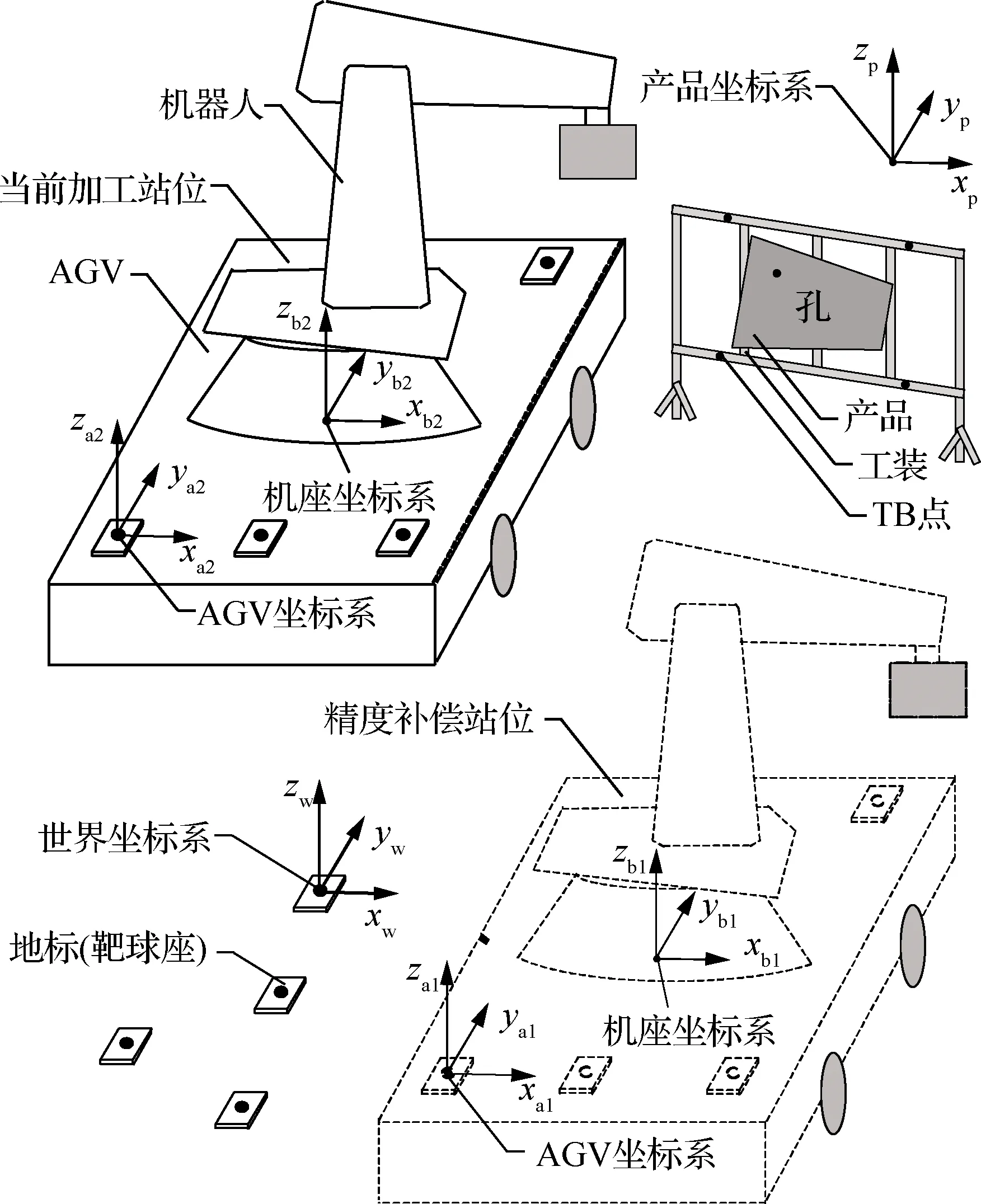
图4 系统中使用的坐标系Fig.4 Coordinate system used in system

图5 各坐标系的空间变换关系Fig.5 Spatial transformation relations of coordinate systems
b2Thole=b2Ta2a2TwwTppThole=(wTa2a2Tb2)-1·
wTppThole=(wTa2a1Tb1)-1wTppThole
(1)
式中:a1Tb1和a2Tb2分别为机器人处于精度补偿站位和当前加工站位处,机座坐标系相对于AGV坐标系的齐次变换矩阵,该变换关系在AGV处于任何站位时都是固定的,因此有a1Tb1=a2Tb2;wTp为产品坐标系相对于世界坐标系的齐次变换矩阵;wTa2为当前加工站位处AGV坐标系相对于世界坐标系的齐次变换矩阵;b2Thole的位置向量即可作为待补偿点的理论位置,可直接使用精度补偿站位的采样值进行精度补偿。
使用测量构建的AGV坐标系作为中间坐标系来重建机器人机座坐标系有以下优势。首先,AGV存在制造误差和定位误差等误差,如果直接使用理论位置对机座坐标系重建,会在机器人机座坐标系处引入较大误差,经过机器人各连杆的传递会被进一步放大;另外,如果通过旋转机器人关节重新测量并构造机座坐标系,重建的机座坐标系会受到机器人重复定位精度以及操作人员的影响,难以与精度补偿站位中构建的机座坐标系保证一致性;而直接通过测量AGV上的固定靶球座来建立AGV坐标系具有较高的重复度,且机座坐标系相对于AGV坐标系的相对位置关系是固定不变的,因此通过中间坐标系进行机器人机座坐标系换站具有较高的重复精度。
2 定位误差分析
2.1 定位误差来源
根据误差的时变性,机器人定位误差可以分为准静态因素和动态因素[21]。准静态因素就是随时间变化缓慢或不变的因素,包括运动学参数误差、温度变化和机械磨损等;动态因素就是随时间变化较大的因素,包括自重或外力等引起的弹性变形、振动引起的定位误差等。
就工业机器人而言,影响末端定位误差的主要因素为准静态因素,而其中又以运动学参数误差为主,约占机器人定位误差的80%~90%[22]。当机器人承载在AGV上时还有动态因素的影响,这是由于机器人在运动过程中,自重、惯性力和外力等变化较大,加之系统振动,会使AGV产生较大的弹性变形,经过机器人各连杆传递放大后,会对末端定位误差产生剧烈影响。
分析系统定位误差来源的目的是找出影响定位误差的主要因素,由以上分析可知影响AGV式移动制孔机器人的主要因素是机器人运动学参数误差和AGV的弹性变形。
2.2 定位误差相似性
从影响AGV式移动制孔机器人定位误差的两个主要误差源分析,只考虑机器人运动学参数误差和AGV弹性变形的影响。对于某个具体的旋转关节串联机器人而言,运动学参数中只有关节转角为变量,一组关节输入对应一个末端位姿,反之,末端位姿在给定的关节约束下也唯一对应一组关节输入,即可认为关节转角变量与末端位姿之间是一一对应的。在机器人运动学参数误差模型中,也仅有关节转角为变量,因此可以认为一组关节输入对应一个位姿,且一个位姿对应一个定位误差。将定位误差看成关节转角的确定性函数,那么定位误差与关节转角之间就存在较强的空间相关性,即每一组关节输入都对应一个定位误差。当各关节输入相近时,对应的定位误差存在相似性。
类似地,当笛卡尔坐标空间中的两个位姿之间越相近时,由机器人自重、惯性力等引起的AGV的弹性变形也趋于相近,由弹性变形的变化引起的末端定位误差的变化也越相似。可以认为在笛卡尔空间中,当各关节输入相近时,由AGV弹性变形引起的末端定位误差也存在空间相似性。
综上所述,从影响AGV式移动制孔机器人定位误差的主要因素出发,可以认为AGV式移动制孔机器人定位误差在空间中具有相似性。且两组关节输入偏差越小相似性越高,对应的末端位置也越近;两组关节输入相差越大相似性越低,对应的末端位置也越远。当两组定位误差之间满足一定相似性时,在一定的误差允许范围内,可以相互替代。扩展到多组相近的定位误差时,任一组定位误差可以由其他定位误差向量及其影响系数进行线性拟合。
3 误差相似性精度补偿
3.1 空间插值与补偿
精度补偿的关键是估计出待补偿点在无补偿状态下的定位误差,AGV式移动制孔机器人误差源不仅包含关节转角误差,还有AGV的弹性变形,要建立一个真实的能反映AGV式移动制孔机器人运动学误差的模型非常困难。基于AGV式移动制孔机器人定位误差在空间中的相似性,考虑用相似的已知对应点对待补偿点进行估计。因此对已知点权值的求解成为误差估计的关键,将已知点权值用待补偿点与已知点之间距离的倒数表示,距离越近的点相似性越强,对应的权值也越大,距离越远的点相似性越弱,对应的权值就越小。这种反距离加权的空间插值方法不用建立复杂的运动学模型,计算过程简单。
为了使采样点在空间中分布足够均匀以利于算法的逼近,且方便补偿时对于相似采样点的选取,将机器人工作空间以一定步长划分为无数立方体网格,网格内包含的所有待补偿点的定位误差都可以用网格的8个顶点的采样值进行估计,原理如图6所示。
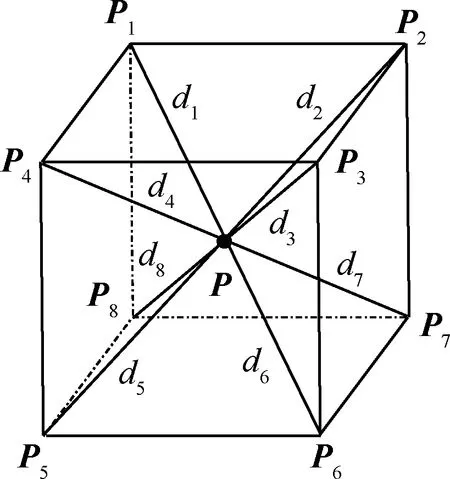
图6 基于反距离加权的定位误差估计方法Fig.6 Position error estimation method based on inverse distance weighting
待补偿点Pc处于点Pi(i=1,2,…,8)为顶点的立方体网格内,用(xi,yi,zi)表示网格顶点的理论位置,用(x′i,y′i,z′i)表示网格顶点实测的三维坐标,则有:
(2)
式中:(Δxi,Δyi,Δzi)为网格各顶点的实际定位误差。
对于机器人工作空间内的任一点Pc采用基于反距离加权的空间插值与补偿算法进行精度补偿的步骤为
1) 搜索待补偿点Pc所在的立方体网格。
2) 求出待补偿点Pc理论坐标(xc,yc,zc)与所在立方体网格顶点实测的三维坐标(x′i,y′i,z′i)之间的距离为
(3)
3) 用反距离加权算法求得网格各顶点在误差估计中对应的权值为
(4)
4) 用各顶点的实际定位误差与对应的权值加权平均,求得待补偿点估计的定位误差为
(5)
5) 用待补偿点估计的定位误差对理论位置进行后置处理,反向修正得到补偿后的坐标值:
(6)
6) 将补偿后的坐标值作为定位指令驱动机器人运动,机器人实际定位将指向理论目标位置。
3.2 最优网格步长
由于机器人定位误差具有相似性,理论上划分的网格越小,待补偿点与网格顶点之间的距离越近,相似性越强。但这并不意味着由相对较小的网格补偿的精度一定比由相对较大的网格补偿的精度更高,这是由于定位误差的分布规律比较复杂,与距离之间并不是单调变化的。选取机器人工作空间内的小范围区域的定位误差分布来说明,为了简化问题,使机器人在保持其余关节角不变的情况下,仅转动A2和A3轴并测量机器人定位误差,各轴变化范围如表2所示。
观察图7中给定的小范围区域内机器人定位误差在x方向的分布情况可以发现,图中Pa点与Pb点之间的关节角变化相对于Pa点与Pd点更大,但Pa点与Pb点在x方向的定位误差差异却比Pa点与Pd点更小,说明此时Pa点的在x方向的定位误差更接近于与其距离更远的Pb点,因此可能出现同一点经由较大的立方体网格补偿出来的精度接近甚至超过经由较小的立方体网格补偿出来的精度的情况。
尽管如此,这种现象在误差变化比较陡峭的情况下是难以存在的。因此,从定位误差相似性的角度看,为了使网格内所有点在补偿后均能满足精度要求,选取的网格步长应尽量小,但同时随着网格划分得越细采样的工作量也随之增大,从工程应用的角度网格数不利于过多。最优网格步长应在满足使补偿后的残差平均值较小,并且标
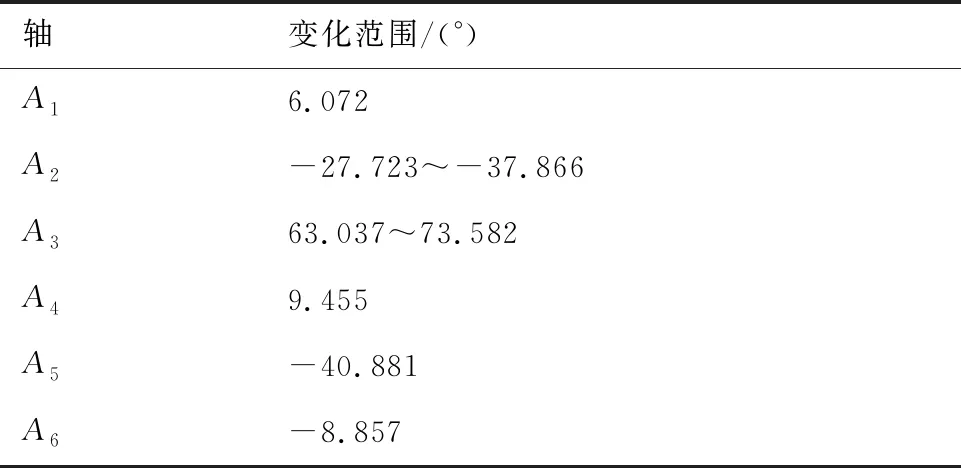
表2 各轴变化范围Table 2 Range of variation of each axis

图7 小范围内机器人x方向定位误差分布Fig.7 Distribution of robot positioning error in x direction in small range
准差也较小的情况下,步长尽可能较大,用最优步长指标stL来表征这种特性,对于不同的网格步长st,对应的最优步长指标值stL越小,该步长越接近最优步长的选取条件:
stL=stAn+stSn-stln
(7)
式中:stAn、stSn、stln分别为步长st下残差的平均值、标准差、对应网格步长归一化的结果,归一化处理为
(8)
(9)
(10)
式中:stA、stS、stl分别为步长st下残差的平均值、标准差、对应网格步长;Amin、Amax分别为各步长下残差平均值中的最小值和最大值;Smin、Smax分别为各步长下残差标准差中的最小值和最大值;lmin、lmax分别为所有网格步长的最小值和最大值。
基于试验数据,通过统计学概率分析,提出一种简单可行的最优网格步长的选取方法。从反距离加权算法的缺陷入手,由式(5)可知,待补偿点处于网格中心时,待补偿点的定位误差估计值相当于网格顶点定位误差的平均值,但当该待补偿点实际定位误差大于网格顶点定位误差的最大值,或小于网格顶点定位误差的最小值时,插值出的估计值的误差将较大。因此考虑在可能存在较大误差的情况下选取试验的步长,在空间中选取几个测试点作为网格中心,且测试点尽量分散在工作空间各个区域以保证普遍性和代表性,然后将网格步长逐步增大。为了检验精度补偿的实际效果,在各步长下对测试点进行反距离加权补偿,测量出补偿后的实际定位误差值即为此时精度补偿的效果值。然后对测试点在每个步长下补偿后残差进行概率统计并计算出平均值和标准差,最后计算各步长下的最优步长指标,在指标值最小附近选取合适步长作为最优网格步长。具体方法为
1) 选取5个以上均匀分散在机器人工作空间中的测试点,以测试点为网格中心,逐步增大步长构建网格。
2) 在各选定的网格步长下,使用反距离加权算法对测试点进行精度补偿并测量补偿后的定位误差。
3) 对测试点补偿后的定位误差进行概率统计,计算出平均值和标准差。
4) 计算各步长对应的最优步长指标,在指标值最小附近合理选取最优网格步长。
4 试验结果与分析
4.1 试验的最优步长
对图1中AGV搭载的KUKA KR480型工业机器人系统选取试验的最优步长步骤为
1) 在机器人工作空间内选取5个测试点,三维坐标分别为Q1(2 600, 0, 1150) mm,Q2(2 500, 350, 1 300) mm,Q3(2 800, 350, 1 000) mm,Q4(2 500, -350, 1 000) mm,Q5(2 800, -350, 1 300) mm。以各测试点为网格中心,从网格步长为20 mm开始,以步幅80 mm 逐步增大到500 mm构建立方体网格,并定义所有网格顶点姿态一致,用RPY角(Roll, Pitch, Yaw)表示为(13.92°, 85.11°, 13.75°)。
2) 用激光跟踪仪测量出5个测试点在每个步长下对应网格顶点的定位误差,对测试点进行精度补偿,为了避免测量过程中随机误差的影响,使机器人重复8次定位至补偿后的三维坐标并测量。
3) 对所有测试点在各步长下多次测量的补偿后的综合定位误差进行数理统计分析:
步骤1根据各步长下测试点综合定位误差的最大值和最小值平均分为多个区间。
步骤2将各区间的最大和最小极值的平均值作为组中值,并求出定位误差在各区间内出现的频数。
步骤3各步长下定位误差平均值为
(11)
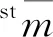
步骤4各步长下定位误差的标准差为
(12)
绘制各步长下综合定位误差平均值和标准差的折线图如图8所示,在步长340 mm和420 mm时分别具有最低的平均值0.199 mm和最低的标准差0.221 mm,且网格步长也较大。
4) 依据式(7)~式(10)计算各步长下的最优步长指标,绘制折线图如图9所示,在步长340 mm 处最优步长指标值最小,为-0.493;步长420 mm处最优步长指标值次之,为-0.409。为方便机器人空间网格划分,选取400 mm作为AGV搭载的KUKA KR480型工业机器人制孔系统的网格步长。
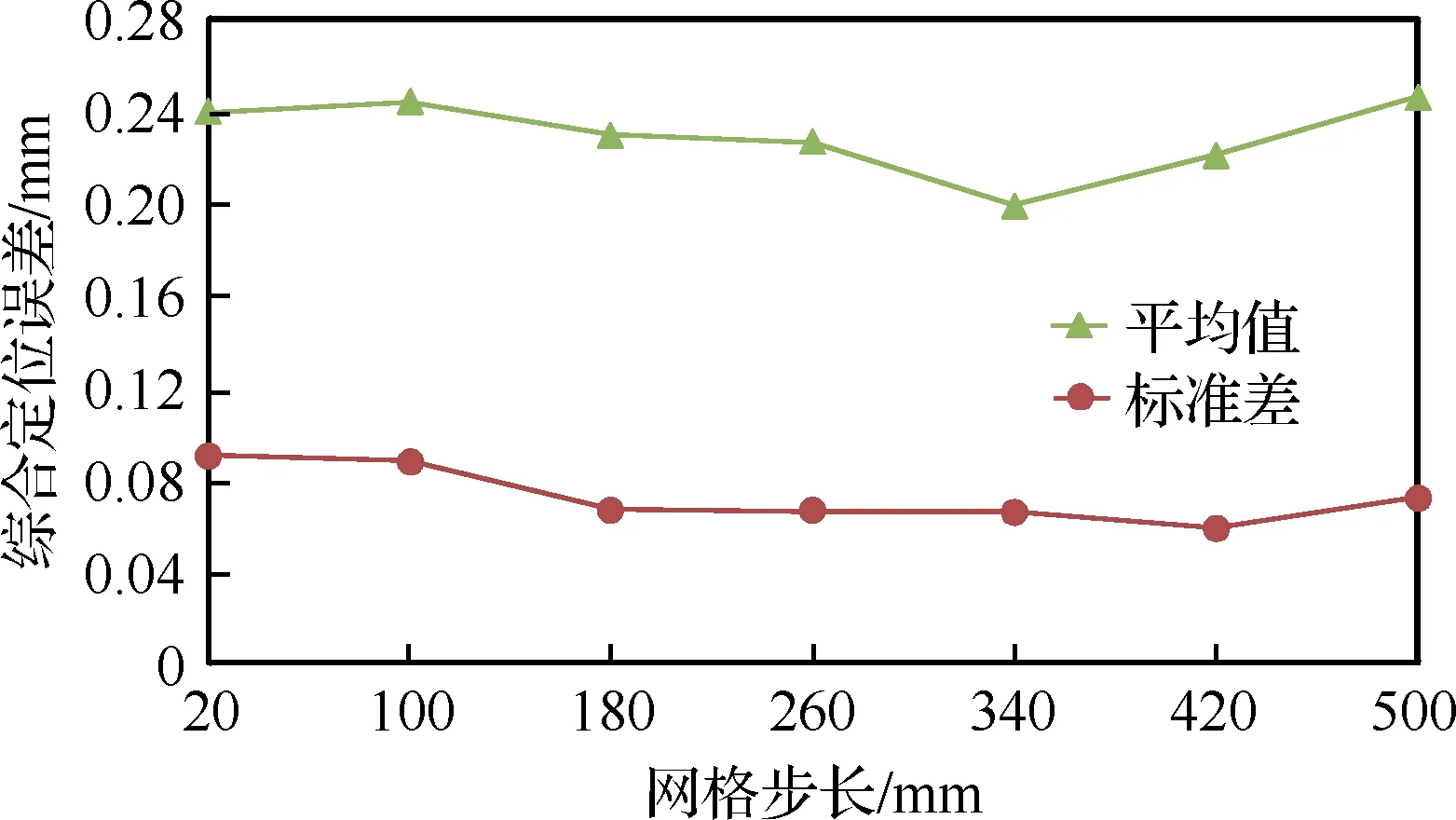
图8 各步长下综合定位误差的平均值和标准差Fig.8 Mean value and standard deviation of comprehensive positioning error under each step
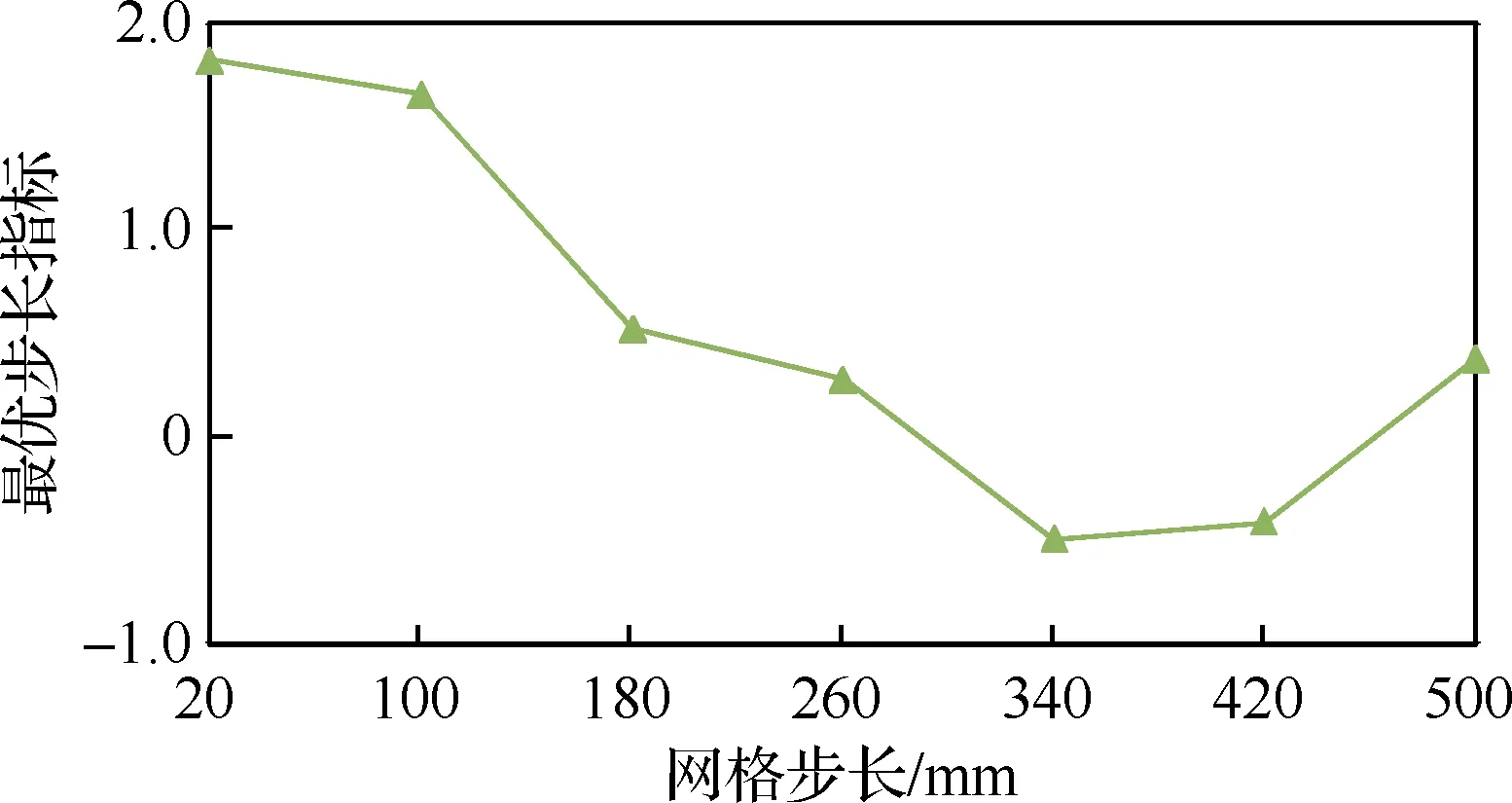
图9 各步长下的最优步长指标Fig.9 Optimal indicator of step under each step
4.2 系统精度补偿
4.2.1 空间插值补偿法
如图10所示,在AGV搭载的KUKA KR480型工业机器人制孔系统中选取了1 600 mm×2 800 mm×1 200 mm的长方体补偿空间,在机器人机座坐标系x,y,z方向范围分别为[1 700, 3 300] mm,[-1 400, 1 400] mm,[400, 1 600] mm。
对基于反距离加权的空间插值与补偿方法进行试验验证,以400 mm步长划分了84个网格,用激光跟踪仪测量网格顶点定位误差。随机选取了276个验证点,绘制补偿后在x,y,z方向和综合的定位误差折线图如图11所示,试验结果统计如表3所示。所有点位均由机器人以固定的姿态角到达,与前文中选取最优步长时一致。
验证点在经过反距离加权法补偿后,综合定位误差最大值由补偿前的2.727 mm降为0.478 mm,平均值由补偿前的1.045 mm降为0.227 mm,标准差由补偿前的0.687 mm降为0.107 mm。系统经过补偿后最大绝对定位误差降低了82.47%,验证了基于反距离加权的空间插值与补偿方法对AGV式移动制孔机器人绝对定位精度的提高可行且有效。

图10 补偿范围和网格划分Fig.10 Compensation range and mesh generation
图11 定位误差折线图Fig.11 Line chart of positional error

表3 验证点数据统计Table 3 Statistical data of verification points
4.2.2 与文献方法比较
为估计待补偿点在无补偿状态下的定位误差,可以通过有限的定位误差采样点数据,建立采样点定位误差与关节角之间的关系模型,文献[9,13]均是通过这种建模方法实现机器人定位误差的映射,从而实现定位误差的识别。
文献[9]是基于机器人运动学参数的误差模型实现机器人定位误差的映射,通过L-M迭代的最小二乘法估计运动学模型中各运动学参数的误差值,这种估计值需要最小化采样点的估计误差与实际误差的区别。其局限性表现在该误差模型仅包含机器人的几何误差源。对于AGV式移动制孔机器人而言,采样点实际误差并非主要由机器人运动学参数误差构成,很大程度上还受到AGV弹性变形的影响,因此在采用该方法计算时机器人雅克比矩阵可能接近奇异,最终可能导致参数辨识的失败。
文献[13]是基于误差相似性建立的定位误差与关节角之间的空间映射模型,并不关注各误差源具体的大小,仅关注末端位置输出和关节角输入,在一定程度上具有良好的通用性。但该空间映射模型的建立以及对待补偿点最优权值的计算,均需要建立相关性矩阵,而这种矩阵是通过输入采样点和待补偿点的关节转角实现的。因此该方法局限性表现在,依赖关节角建立模型的方法在AGV式移动制孔机器人中应用时,当AGV变形程度较大,对定位误差的影响程度也较大时,不利于空间映射模型的建立。
本文提出的基于空间插值的定位误差估计方法无需建立关节转角与定位误差之间的关系模型,且对于空间内的所有待补偿点的定位误差,都可以通过包含它的立方体的顶点进行估计。与文献[9,13]相比优势在于:
1) 无需建立误差模型,计算过程简单,使用较少的采样点即可对待补偿点定位误差进行估计。
2) 使用反距离加权仅依赖于待补偿点与采样点之间的绝对距离,对于关节角并不敏感,因此在满足误差相似性的前提下对各种误差源具有良好的包容度。
3) 在AGV式移动制孔机器人中,在合理选取步长的情况下,不但能有效提高系统定位精度,而且能极大地提高机器人精度补偿的有效范围。
为验证文献[9]和文献[13]方法对于AGV式移动制孔机器人的补偿可行性和补偿效果,选定一个小范围的长方体试验空间,为简化问题,在保持机器人在y方向和z方向补偿范围固定的情况下,仅改变x方向的补偿范围,同时测量图1中靶球2所在观测点离差,探究机器人在x方向不同区域运动时引起的AGV弹性变形变化,以及由此对于文献[9]和文献[13]方法可行性的影响。
在4.2.1节的试验空间中选定x,y,z方向范围分别为700 mm×700 mm×600 mm的长方体空间。保持y和z方向试验范围分别为[-350, 350] mm和[1 000, 1 600] mm,改变x方向的试验范围,从x方向起始范围[1 700, 2 400] mm开始,每次将试验空间向x方向移动100 mm,直到[2 200, 2 900] mm,共选取6个试验空间。在每个试验空间中随机选取了300个采样点,另外再分别选取89个验证点,使用激光跟踪仪测量每个试验空间中采样点误差以及对应的观测点离差,然后分别使用文献[9]和文献[13]的方法对验证点进行精度补偿。结果统计如表4所示。
文献[9]方法在6个试验空间中均无法计算出机器人运动学参数误差,计算结果显示雅克比矩阵接近奇异,验证了该方法并不适用于AGV式移动制孔机器人。
文献[13]方法在x方向范围为[1 700, 2 400]mm,[1 800, 2 500] mm,[1 900, 2600] mm的试验空间内能有效补偿,这3个区域内观测点最大离差为0.066 mm,平均值最大为0.036 mm,标准差最大为0.008 mm;但在x方向的试验范围为[1 700, 2 400] mm,[1 800, 2 500] mm,[1 900, 2 600] mm的试验空间中无法拟合出机器人定位误差与关节角输入之间的空间映射模型,这3个区域内观测点的离差范围、平均值和标准差均比前3个区域大,可以认为此时AGV弹性变形程度相较于前3个区域更大,对于末端定位误差的影响程度也更大。因此可以认为文献[13] 只能在AGV变形程度在一定范围之内时适用于移动式机器人。
综合以上分析和试验验证,本文提出的基于误差相似性的基于反距离加权定位误差的空间插值与补偿方法,能够克服文献[9,13]在AGV式移动制孔机器人精度补偿的缺陷,在有效提高系统绝对定位精度的同时,极大地扩大精度补偿的范围。
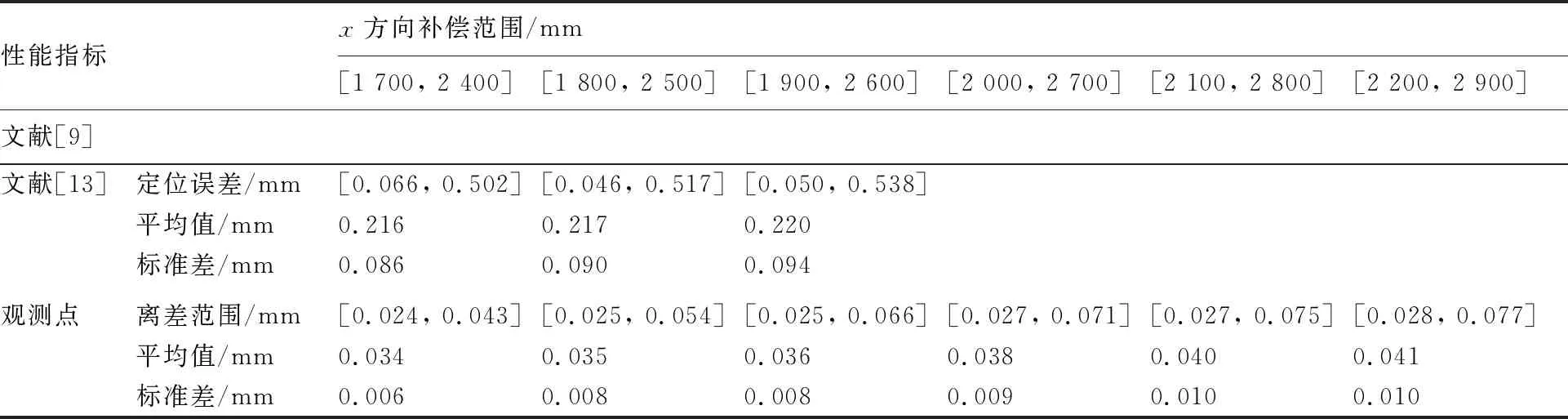
表4 不同补偿区域中的补偿效果Table 4 Compensation effect in different compensation areas
5 结 论
1) AGV式移动制孔机器人定位误差的主要影响因素是机器人关节转角误差和AGV的弹性变形,难以建立准确的物理模型,因此利用定位误差的相似性进行补偿。
2) AGV换站时利用AGV坐标系对机器人机座坐标系重建,具有较高的重复精度,为工程应用和系统升级维护提供了方便。
3) 空间插值补偿方法能克服AGV对于机器人系统定位误差的影响,试验表明能将AGV式移动制孔机器人绝对定位精度平均值提高到0.227 mm,最大定位误差降低到0.478 mm。
4) 在测量网格顶点定位误差时均让机器人以固定姿态到达,对于变姿态的情况还有待进一步研究。
