城市轨道交通共线运营下的开行方案优化研究

文∕黄欣荣、赵前程

1 共线运营的定义

目前，城市轨道交通主要采用共线运营方式，它借助轨道交通良好的通达性，列车可以在临近线路之间进行跨线运营，这使得在同一线路段内可能同时存在多条列车共同运营的情况。

2 “Y”字型共线运营

主、支线是相互独立运营的，同时也可以相互连贯运营。一般来说，主线是主要客运线路，支线主要支持换乘。不管是主线还是支线，承担的客运量压力都较大；主、支贯通运营时，在两线之间有较大的换乘客流量，且主线承载的客运量相对更大。

从下图1 中可以看出，南京地铁一号线采用了Y 型线结构设计。南京站-禄口机场主线承担了较大的客运量，因此主、支线是相互独立的，s1 号线就是支线。

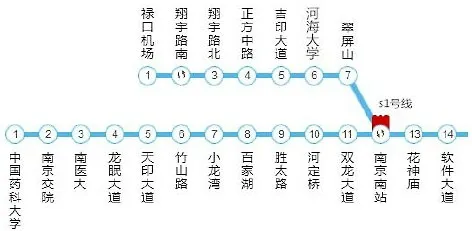
图1 南京地铁一号线示意图

3 城市轨道交通Y 型线开行方案优化研究

3.1 问题描述及基本假设

3.1.1 城市轨道交通Y 型线路描述

从下图2 中可以看出，这是典型的Y 型轨道交通运用线路。该线路一共包括N 个车站，O 站到d1站属于主线路段，主要是全线贯通的大交路，列车从两个末端车站之间来回运行；s1站到d2站属于支线路段，使用小交路运营，在s0站折返，s0站至d2站之间属于小交路运行路段。大交路发车频率为f1、发车间隔为h1，小交路发车频率为f2、发车频率为h2，g 代表大、小交路的发车间隔，我们将该主支线分为四个运营路段，分别用M1、M2、M3、M4代表。

图2 城市轨道交通Y 型线共线示意图

3.1.2 基本假设及定义

3.1.2.1 基本假设

本文做出以下几个假设条件：

（1）乘客到站时间匀速分布，不存在乘客滞留车站的情况；

（2）乘客搭乘列车是最理性合理的，直达列车乘客与换乘乘客之间不会改变自己的出行方案，各自选择就近的一列列车上路；

（3）大小交路路线是相互独立运营的；

（4）Y 型路段上的列车成对发车；

（5）每一个车站都可支持列车双向折返，且折返时间没有差异；

（6）列车型号是不变的，列车的载客量是固定的，且是一个常数；

（7）列车每站都会停靠，不会越站运营，在每一个路段的行驶速度都是相同的。

3.1.2.2 函数定义

为便于本文研究，相关函数定义如下：

（1）Dkl：代表在k站上车，l站下车的乘客人数。

（2）D+k：代表在k站上车，在第l1l2站下车乘客人数，“+”代表上行列车。

（3）D-k：代表在k站上车，在第l1l2站下车乘客人数，“-”代表下行列车。

3.1.2.3 符号定义

为便于研究，本文使用的符号定义如下所示：

C-车辆额定载客量；f0-列车发车最小频率；f1-大小交路列车运行频率；f2-代表大小交路发车频率；fm-代表某一段线路最大列车通过量；h1-代表交路上列车发车间隔时长；h2-代表列车之间的运营间隔时长；g-代表不同交路上列车的发车时长；m-代表交路发车间隔之比，-列车发车次数；α-交路编码，α=1 代表大交路，α=2 代表小交路；s0-小交路往返站；ηα-大、小交路列车最大运量率；ηm-列车最大载客量；Lα-交通路路段里程；να-交路列车行驶速度；Qα,r-代表第r个区间内大、小交路断面客流量；Q1-大交路上载客量；Q2-小交路上的载客量；δ-站点之间的作业时间；ti-第i个路段运营时间；ts-列车安全间隔时间；td-交路列车靠站停留时长。

3.2 城市轨道交通Y 型线共线开行方案模型的构建

在设计城市轨道交通运营线路时，如果从乘客需求出发，那么要最大程度压缩候车时间，这主要通过增加发车频率来实现；从列车运营来看，在保证客运量的同时，有效控制列车发车频率，降低成本，提高列车载客效率。本文综合考虑上述两个方面的需求，优化Y 型线运营方案。

3.2.1 客流分析

根据乘客出行需求，我们将客流分为九种类型，同时将整个路段分为四个子运行区间，M1区段：O 站到s0站；M2区段：s0站到s1站；M3区 段：s1站到d1站；M4区 段：s1站 到d2站。在下图3 中，给出的是上行方向的分段图。

图3 Y 型线路客流示意图

第一类客流：乘客起始站都在M1区段上，乘客只搭载大交路列车，这类列车的发车频率为f1。

第二类客流：乘客在M1区段站台上车，在M2区段内的站台下车，乘客只搭载大交路列车出行，不涉及到复杂换乘方案，这类列车发车频率为f1。

第三类客流：乘客在M1区段站台上车，在M3区段站台下车，乘客只搭载大交路列车出行，这类列车发车频率为f1。

第四类客流：乘客在M1区段站台上车，在M4区段内的站台下车，乘客搭乘大交路列车（发车频率f1）到M2区段下车，再换乘小交路列车（发车频率f2）。

第五类客流：乘客出发、终点站都在M2区段内，该路段同时有两交路列车运营，乘客有两种搭乘方案选择，该路段发车频率为f1+f2。

第六类客流：乘客在M2区段站台上车，在M3区段内的站台下车，乘客只搭载大交路列车出行，该路段列车发车频率为f1。

第七类客流：乘客在M2区段站台上车，在M4区段站台下车，乘客选择小交路列车出行，该路段列车发车频率为f2。

第八类客流：乘客出发站和到达站都在M3区段内，乘客只搭乘大交路列车出行，该路段列车的发车频率为f1。

第九类客流：乘客出发站和到达站都在M4区段内，乘客只搭乘小交路列车出行，该路段列车发车频率为f2。

3.2.2 目标函数

（1）乘客出行成本

本文乘客交通成本主要包括两个部分：候车时间和在途时间。假设所有列车运行速度都是一样的，列车运营方案调整不会影响乘客的出行时间成本，只是候车时间是可变的，因此只将候车时间作为出行时间成本。

在计算乘客候车时间时，要针对上、下行列车区分对待，并根据OD 对乘客进行区段划分，根据不同客流量以及上下车区段计算候车时间，将上、下行候车时间相加就是乘客的总出行时间。

M1区段上行乘客候车时间为：

M2区段上行乘客候车时间为：

M3区段上行乘客候车时间为：

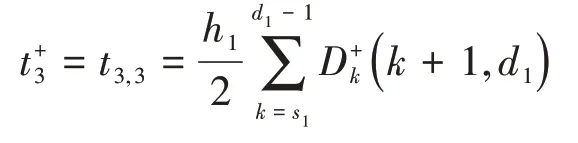
M4区段上行乘客候车时间为：

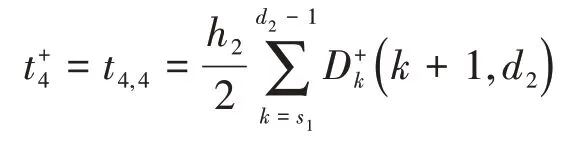
则上行乘客候车时间为

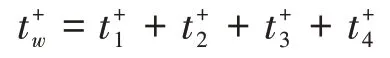
M1区段下行乘客候车时间为：

M2区段下行乘客候车时间为：

M3区段下行乘客候车时间为：

M4区段下行乘客候车时间为：

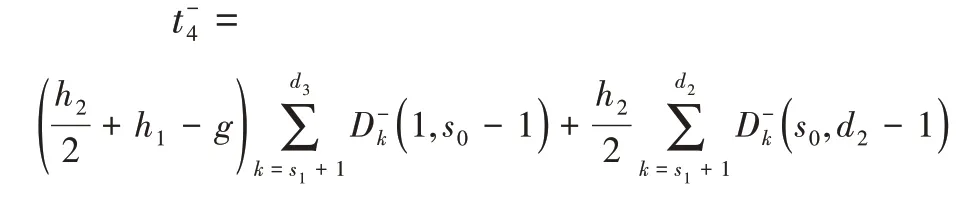
那么，下行列车的候车时间为：

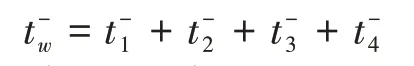
综上所述，我们可以建立乘客最小候车时间函数：

（2）企业运营成本

列车运营成本主要包括两个部分，即人力资源成本和列车运营成本。列车运营里程与维护成本、能耗成本成正比，因此列车运营成本用列车行驶里程来代替。因为列车运行时间与人工成本有很大的关联性，因此用列车运营时间代替人力资源成本。

综上所述，企业运营成本函数主要包括两个变量，那就是列车运营里程以及运营时间，具体可见下式。

列车最小运营里程：

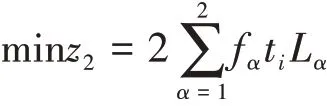
列车最小行驶时间：

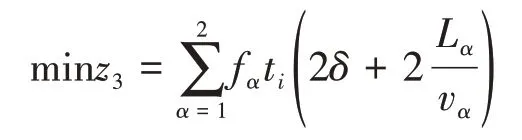
（3）约束条件

本模型的约束条件：

在上述约束条件中，式1 代表线路通行限制；式2 代表小交路往返点分布；式3 代表最小发车频率，交通线路最大载客量以及最大、最小发车频率；式4 代表列车最大载客量；式5 是指列车发车占比数，要避免出现行车冲突，必须要保证大交路发车间隔为小交路发车间隔的整数倍；式6 代表客流交通需求条件；式7 代表大、小交路行车间隔条件。

由于大小交路发车是不均衡的，因此它们的发车频率有所不同，这里要对大小交路列车行车间隔进行识别，具体可见下图4。本文将列车停站时间、行车安全间隔作为大小交路列车行车间隔约束条件。

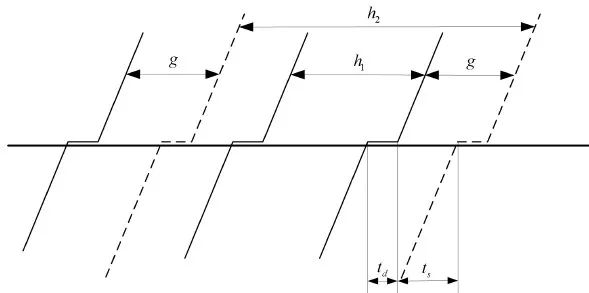
图4 大、小交路行车间隔示意图

4 算法设计

遗传算法是一种比较先进的模拟算法，其是一种全局搜索优化算法。下面，本文对遗传算法具体实施过程进行详细介绍。

4.1 编码

本文模型一共包含四个决策变量，使用二进制编码方式对变量进行描述，每条染色体包含4 段基因信息。

图5 染色体编码示意图

4.2 适应度函数

在设计城市轨道交通 Y 型线列车运行线路方案时，可以通过建立一个总目标函数来描述。这个总目标函数具体如下所示：

4.3 选择

选择是指在样本中选择一个比较有代表性的个体代表全部样本。本文使用轮盘赌法计算各个个体适应度与适应度总和之比，每个个体被选为样本的几率计算方法如下：

4.4 交叉

事先要设定交叉概率，它介于[0，1]区间范围内。如果随机生成概率＞交叉概率，那可以直接进入到下一个操作环节，无需进行交叉操作；如果随机生成概率＜交叉概率，那就确定两个交叉操作个体，这个操作步骤循环到满足所有前置条件结束，否则需要重新开始前面的操作，具体操作步骤如图6 所示。

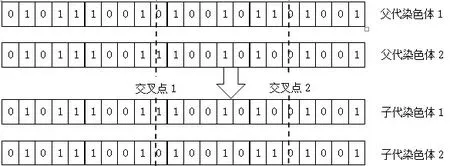
图6 交叉操作示意图

4.5 变异

确定一个变异概率，其介于[0，1]区间内，在这其中随机选取一个数，如果随机生成概率＞变异概率，则直接进入下一个环节，无需进行变异操作；如果随机生成概率＜变异概率，则确定变异个体进入操作过程，具体步骤如下图7 所示。

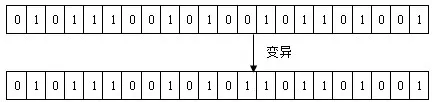
图7 变异过程示意图

5 结语

本文对Y 型线路进行了分区，将其一共分为4 个区间。根据乘客出行需要，将其分为九个类别，对每一个类别乘客进行分析，总结出其搭乘规律。建立一个目标函数，其变量包括候车时间、列车运行里程以及时间，综合考虑了列车通行能力、最大载客量、发车频率等限制条件，根据交流发车频率、站台折返点以及发车间隔作为变量，建立了一套Y 型线列车运行线路优化模型，以最大节省列车运营成本和乘客交通成本。建立模型之后，将具体问题转化为单目标函数求解问题，并使用遗传算法求解函数。