考虑零售商销售努力的双渠道供应链定价策略研究

张霖霖 孙坤鹏

（北京工商大学 商学院，北京 100048）

一、引言

近年来，信息技术的发展使得电子商务市场更加繁荣，从而使制造商在产品销售渠道方面有了更多选择。《2017-2018中国电子商务发展报告》显示，商品类电子商务交易额达到了16.87万亿元，比2016年增长21%，这表明电子商务创造出了新商机。面对电子商务带来的新商机，越来越多制造商在加速建设线上直销渠道，积极融入电子商务大潮中。制造商线上直销渠道的开辟，不仅便利了消费者，也丰富了我国商品销售市场层次。例如海尔集团成立初期，生产出的产品大多由线下零售渠道进行销售，但随着市场对产品需求量的增加，以及海尔集团产品种类不断增加，传统单一销售渠道已经不能满足企业进一步发展需求，所以海尔集团正在加速建设线上直销渠道来应对市场变化，进而满足企业进一步发展的需要。

线上直销渠道的建设，虽然提升了制造企业的产品分销能力，也造成了线上直销渠道与线下零售渠道之间的竞争与冲突，这种竞争主要体现在价格以及服务等方面的竞争，线上直销渠道由于其结构扁平，所以销售成本较低，线下零售商为了应对线上直销渠道的成本优势，需要在销售环节做出更多努力来提升服务质量以及用户消费体验，从而提高销量。因此，将线下零售商的努力考虑到定价策略中是十分有必要的。笔者将零售商销售努力考虑在内，对双渠道供应链中的定价策略进行研究，并且对在销售努力条件下，供应链中的其他因素，如市场潜在需求、交叉价格弹性系数以及渠道占市场比例等对供应链定价策略的影响进行了研究。

二、文献综述

关于双渠道供应链定价策略的研究，目前已有大量理论与实证研究成果。我们将从双渠道供应链定价策略以及销售努力这两个方面来回顾近年的相关研究成果。

双渠道供应链定价策略方面，王玉燕等(2006)通过博弈论模型，对供应链中的定价策略进行研究，得出供应链中的成员在合作博弈与非合作博弈中的均衡解，给以后的相关研究提供了思路。[1]Li Tao等(李涛等，2018)则针对目前供应链中零售商在定价方面话语权不断上升的情况，分析了权力结构对于供应链定价的影响，研究发现供应链成员在不同权力结构下都能从扮演领导者的角色中获得更多的利润。[2]有些学者分析了不同风险偏好与不同渠道偏好对供应链收益的影响。许民利等(2016)通过研究发现在不同风险偏好程度下，供应链成员会采取不同的定价策略，制造商风险偏好程度一定，那么随着零售商风险规避程度的增加，零售商制定的最优价格降低，最优批发价增大；当零售商风险偏好程度一定时，随着制造商风险规避程度的增加，制造商和零售商制定的最优价格均降低。[3]林晶和王健(2018)则发现当消费者对双渠道供应链中某一渠道偏好时，制造商会在该渠道上采取优质高价的价格策略，各个渠道的价格与消费者对该渠道的偏好程度成正比。[4]由此可见，在有关影响供应链定价因素的研究当中，对销售努力的研究较少。随着双渠道供应链的普及，渠道间的竞争势必会日益激烈，可以预见将来会有越来越多的线下零售企业会采取更多的销售努力行为，来面对制造商线上直销渠道的竞争。李建斌等(2016)对供应链内的预设价格进行了研究，发现当预设价格的上限低于某一临界值时,随着成本的增加,制造商的最优策略从固定价格转变为单一报价的定价策略;如果预设价格上限超过这一临界值,制造商则会选择固定价格的定价策略。[5]浦徐进和龚磊(2016)通过构建由制造商主导的二级双渠道供应链，研究了在“搭便车”效应影响下双渠道供应链中的定价策略，研究发现新进入市场的消费者“搭便车”行为会降低零售商的促销力度，同时线上直销渠道价格会较为明显低于线下零售渠道价格，进而不利于供应链整体利润水平的提高。[6]Zhao J等(赵等，2014)和韦才敏等(2018)研究了在不同竞争行为中的供应链定价策略。Zhao J等(赵等，2014)利用博弈论的方法研究得出了制造商与零售商在古诺、Stackelberg竞争模式下的均衡解。[7]韦才敏等(2018)则是给出不同市场竞争模式以及集中决策模式下供应链成员的博弈均衡解。[8]然而张玉忠等(2016)发现合作博弈决策在任何情况下都要明显地优于完全非合作博弈决策以及局部合作博弈决策，因此在竞争日益激烈的背景下，供应链中的成员应通过合作的方式来提升供应链的整体收益。[9]刘昊等(2017)在强势制造商背景下，研究了多渠道供应链定价策略，通过分析发现制造商对于线下零售商的价格指导有利于缓解渠道间的价格冲突，推动供应链中的产品销售，但这样会对供应链中线下零售商的收益产生不利影响，因此需要通过收益协调机制促进供应链的整体发展。[10]在供应链协调机制方面，梁喜等(2018)在制造商主导的双渠道供应链中，通过研究得出制造商在保证一定的佣金比例时，制造商的利润与佣金比例系数成反比，而零售商的利润与佣金比例系数成正比。[11]祖峰等(2017)通过Stackelberg模型求解，发现制造商通过实施补偿激励能够增加自身以及零售商的收益,同时供应链的整体收益也会相应得到提升，并且在实施补偿激励之后，线上直销渠道价格、线下零售渠道价格均得到上涨。制造商线上直销渠道的建立，使线上直销渠道占据了一些原本属于线下零售渠道的市场份额。线下零售商在面对线上直销渠道的竞争时，会采取一定的销售努力行为来争取更多的市场份额。因此，在研究双渠道供应链定价策略的过程中，将销售努力的因素考虑在内是十分必要的。

在销售努力方面，覃艳华和曹玮嘉(2014)分析了在考虑销售努力因素下双渠道供应链的定价策略以及订货量策略。[12]吴正祥和李宝库(2017)通过构建双渠道供应链模型，利用博弈论方法，研究了在不同批发价格模式下，供应链中销售努力对于各个成员最优价格制定的影响。[13]方磊等(2018)将零售商的销售努力和供应链的运营融资问题相结合，进而研究资金不足的零售商分别通过银行贷款和股权融资时，供应链的最优运营策略。[14]可以看出，目前在双渠道供应链定价策略领域结合销售努力进行研究的成果较为少见，并且大多仅仅考虑了销售努力对定价策略的影响，没有考虑供应链中其他因素对于定价策略的影响，如市场潜在需求、交叉价格弹性系数以及渠道占市场比例等。

电子商务市场的繁荣将会带动更多制造商建设线上直销渠道，而线上直销渠道的建立势必会促使线下销售渠道中的零售商在销售环节做出更多的销售努力来应对来自线上直销渠道的竞争。可以预见，销售渠道之间的竞争将会日益激烈。综上所述，笔者在研究双渠道供应链中的定价策略时，将传统销售渠道中零售商的销售努力考虑其中，并且研究了在销售努力条件下供应链中其他因素，如市场潜在需求、交叉价格弹性系数以及渠道占市场比例等对于定价策略的影响，进而得出更加全面、更加贴近现实的结论。

三、模型构建以及符号说明

1.模型构建

图1 双渠道供应链结构图

如图1所示，构建一个包含线下零售渠道和制造商线上直销渠道的二级双渠道供应链。制造商以w的批发价格经由线下零售商销售产品，以价格P2通过自身建立的线上直销渠道销售产品。线下零售商以w的批发价购进商品，以P1的价格通过线下渠道向消费者进行售卖。在售卖的过程，线下零售商通过销售努力来提升顾客的消费体验，进而提升产品销量。

2.符号说明

D1：线下零售渠道需求

D2：线上直销渠道需求

P1：线下零售渠道零售价格

P2：线上直销渠道零售价格

W:批发价,P1≥P2＞w

β:线下销售渠道和线上直销渠道之间的交叉价格弹性系数

θ：线下零售商在不采取销售努力行为时所占市场份额

C：线下零售商采取销售努力所付出的成本

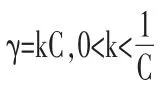
πnm：m决策模式下成员n的收益，m=C,DE,C代表集中决策，DE代表分散决策

a:市场潜在需求

四、重要假设

笔者研究的是单一产品制造商同时拥有线下零售渠道和线上直销渠道时的双渠道供应链定价策略，重要假设有以下几点：

1.供应链中的成员均为独立实体，并且信息对称；

2.制造商的产能能够满足市场需求，即不会出现供不应求的情况。

五、策略分析

1.集中决策下的策略分析

在集中决策模式下，制造商和零售商组成了一个战略联盟，供应链中成员的目的都是使整个供应链收益最高，渠道之间的竞争将会被淡化，零售商无需采取额外的销售努力来提升销量。因此在集中决策模式下，需求函数以及收益函数具体如下：

将（1）和（2）带入（3）中得：

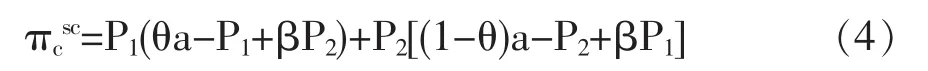
对（4）求二阶导可得：

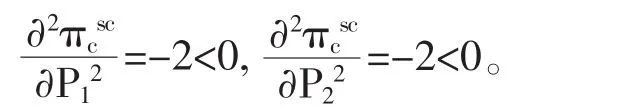
因此，收益函数关于P1和P2均为凸函数。综上所述，在集中决策下收益函数存在最优解且最优解是唯一的。

为了得出最优解，收益函数应满足以下一阶条件：

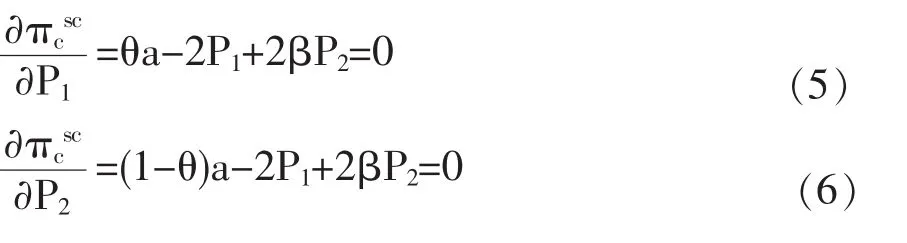
联立（5）和（6），求得在集中决策情况下的最优价格P1*和P2*为：

将（7）和（8）带入（1）和（2）中得:

将（7）至（10）带入到（3）中得：

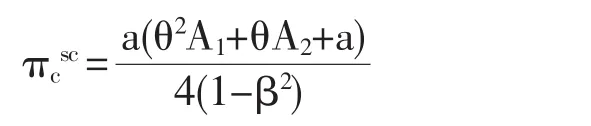
其中

A1=2-2β+a-aβ

A1=2β-2a+aβ

命题1：线下零售渠道与线上直销渠道之间的价格差异随着两个渠道的潜在需求量之间的差异增大而增大。

｜P2*-P1*｜表示线下零售渠道与线上直销渠道之间的价格差异，｜(1-θ)a-θa｜表示线下零售渠道与线上直销渠道之间潜在需求的差异，如（11）所表示，随着线下零售渠道与线上直销渠道之间潜在需求差异的增加，线下零售渠道与线上直销渠道之间的价格差异也随之增加。

命题2：在集中决策的模式下，线上直销渠道的最优价格与线下零售渠道的最优价格均与潜在需求成正比。

将P1*与P2*对a求导，可得：

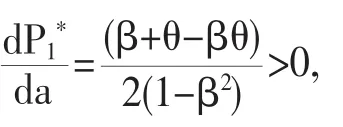
2.分散决策下的策略分析

在分散决策模式下，制造商、零售商之间进行Stackelberg博弈。Stackelberg博弈即在供应链中占据主导地位的一方以最大化自身利益为出发点来制定价格，另外一方在已知主导一方所制定价格的情况下，来决定自身的价格。制造商对零售商的批发价为w，同时以P2的价格通过线上直销渠道销售商品。线下零售商以w的批发价购进商品，以P1的价格通过线下渠道向消费者进行售卖。在售卖的过程中，线下零售商通过销售努力，如投放广告，提升服务水平等方式来提升销量，C为线下零售商采取销售努力所付出的成本，γ为通过销售努力所获得的市场份额。因此在分散决策的模式下，需求函数以及收益函数具体如下：

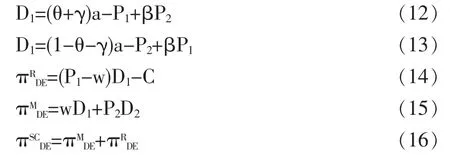
因此，在分散决策的模式下，供应链成员的最优定价策略应满足下列方程组：

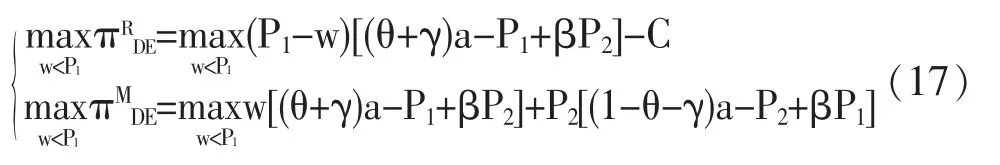
对方程组（17）求解，得到纳什均衡（P1*，P2*）：

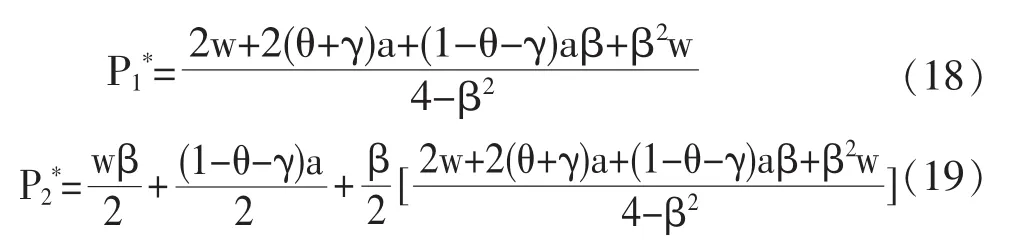
将（18）和（19）带入（12）和（13）中求得各渠道需求为：

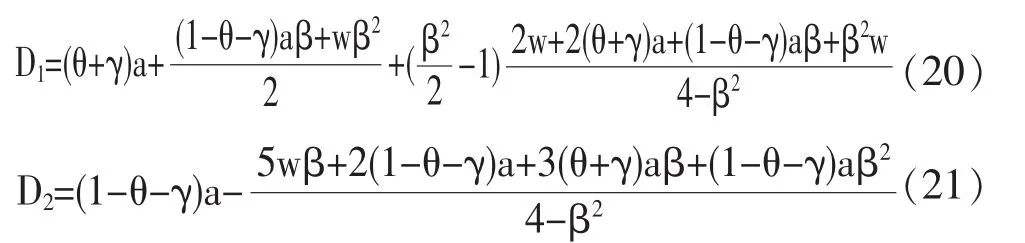
命题3：无论是线下零售渠道还是线上直销渠道的价格，均与潜在需求a成正比。

利用（18）和（19）对 a求导可得：

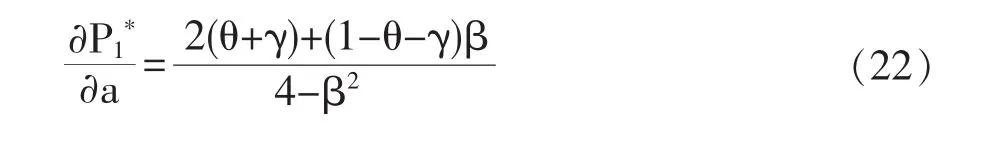
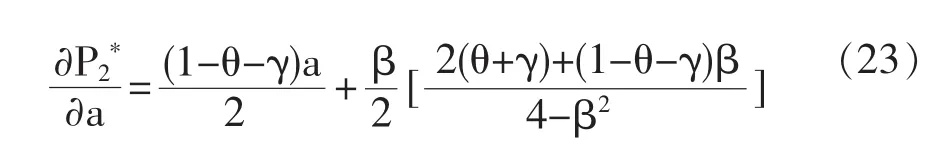
命题4：线下零售渠道的最优价格随零售商的销售努力程度的增加而增加，线上直销渠道的最优价格随着零售商的销售努力程度的增加而减少。

因为 γ=kC，利用（18）和（19）对 C 求导可得：

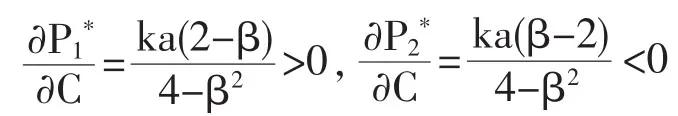
但是随着线下零售商销售努力的增加，其销售努力成本C也在不断增加，成本的增加可能会让线下零售商的利润减少。

利用（14）对销售努力成本C求导可得：

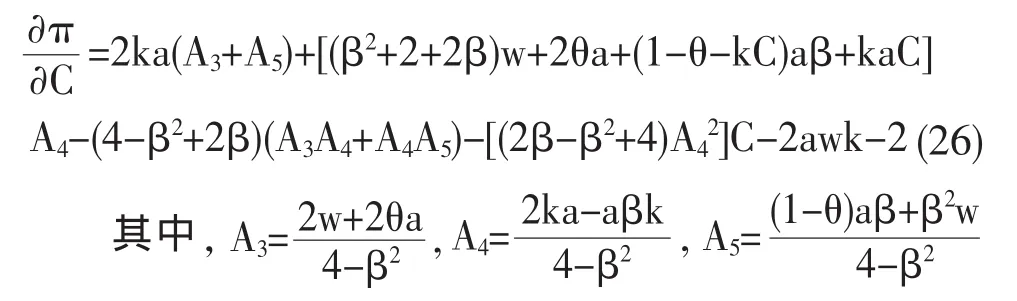
当收益最大时，(26)=0，解得最佳销售努力成本为：

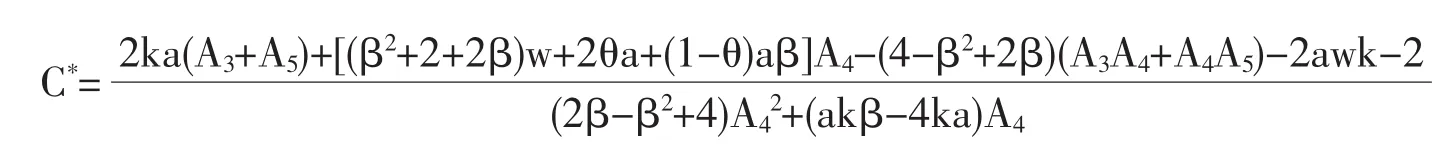
通过以上分析，我们发现线下零售商投入过多的销售努力会减少其收益。只有当线下零售商投入恰当的销售努力时，才能在占据一定市场地位的同时，避免过度竞争，进而获得最大收益。

3.不同决策模型的对比分析

以上两节分别在集中决策与分散决策的模式下对双渠道供应链中的参与者的定价策略进行了研究，本节将从交叉价格弹性系数β对P1和P2的影响，以及线下销售渠道所占市场份额θ对P1和P2的影响，对以上两个决策模型进行对比分析。

表2 集中决策与分散决策中，P1*和P2*与交叉价格弹性系数β之间的关系

因此从表2中可以看出，无论在集中决策还是分散决策的模式下，P1*和P2*均随着交叉价格弹性系数β的增加而增加。

表3 集中决策与分散决策中，P1和P2与线下渠道所占市场份额θ之间的关系

六、结论与展望

笔者通过构建了一个包含线下零售渠道和线上直销渠道的二级双渠道供应链，并且将线下零售商的销售努力行为考虑在内，针对双渠道供应链中的竞争分别研究了在集中决策和分散决策模式下，制造商与线下零售商的定价策略。研究发现，在集中决策模式下，线下零售渠道与线上直销渠道之间的价格差异随着两个渠道潜在需求量之间差异的增大而增大，并且两个渠道的最优价格与市场潜在需求成正比。在分散决策模式下，两个渠道的最优价格亦与潜在需求成正比，并且P1随着线下零售商销售努力的投入的增大而增大，而P2随着线下零售商销售努力的投入的增大而减小。因此，当线上直销渠道在面对线下零售商通过采取更多销售努力行为来争取更多的市场份额时，制造商会通过降低价格的方式来应对线下零售渠道的竞争，但是线下零售商投入过多的销售努力，会减少其收益。只有当线下零售商投入恰当的销售努力时，才能在占据一定市场地位的同时，避免过度竞争，进而获得最大收益。

通过研究我们还发现，无论在集中决策下，还是在分散决策下，两个渠道的最优价格均与两个渠道之间的交叉价格弹性系数β成正比。另外，两个渠道的最优价格随着各渠道所占市场份额的增加而增加。综上所述，只有保持供应链的协调发展，平衡供应链渠道之间的权力结构，避免垄断情况的出现才能切实维护消费者的利益。