高速磁浮列车长定子直线同步电机电磁解耦特性分析

袁贤珍，辛本雨，石 煜

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

TR型常导高速磁浮系统是一套长定子电励磁直线同步电机系统。由于直线同步电机自身独有的结构特点，如空载反电动势、端部效应、齿槽效应及直线发电机磁场等，使得电机内磁场分布情况复杂，易产生牵引力波动并干扰悬浮力。目前，国内外学者对直线同步电机的磁场分布已做了许多研究，如文献[1]研究了长定子直线同步电机磁场分布；文献[2-3]对长定子直线同步电机内磁场进行了分析和测量；文献[4-5]基于ANSYS有限元软件对长定子直线同步电机电磁场瞬态特性分析；文献[6-7]采用有限元法对高速大推力直线电机进行了电磁力特性分析；文献[8]以TR08型车用同步电机为研究对象进行了电机磁场分析及电感参数计算。但这些研究均是基于理想化的建模。为了更好地解决实际工程应用时存在的悬浮电磁场与牵引电磁场不完全解耦引起的互相干扰问题，本文将充分考虑实际车辆安装工况，建立长定子直线同步电机仿真模型，借助于有限元法求得长定子直线同步电机电磁场的近似解，以获得高速磁浮列车长定子直线同步电机内磁场分布特点和牵引力与悬浮力的计算方法，能够更加精确地指导高速磁浮牵引系统的工程设计。

1 长定子直线电机电磁场分析

高速磁浮列车通常由端车和中间车辆组成，其中端车有14个整体悬浮电磁铁和2个半体悬浮电磁铁，中间车有14个整体悬浮电磁铁和4个半体悬浮电磁铁。相邻两车的半体悬浮电磁铁组成一个整体悬浮电磁铁，相邻整体悬浮电磁铁的几何中心间距为3 096 mm。一个整体悬浮电磁铁包括10个宽体磁极和2个窄体磁极，窄体磁极被布置在悬浮电磁铁两端，只有宽体磁极顶部布置有发电机绕组，励磁磁极极距为266.5 mm。为了方便建模分析，本文以一个悬浮架、长度为3 096 mm的长定子直线同步电机作为研究对象，在有限元软件中建立长定子直线同步电机模型，分别对其空载和负载两种工况进行仿真计算。

1.1 长定子直线同步电机组成

根据高速磁浮列车电磁铁特点分析，本文研究对象为一个独立的标准直线电机，其包括一个由10 个宽体磁极和2个窄体磁极组成的悬浮电磁铁以及3个定子铁心。长定子直线同步电机各部分组成见图1。

1.2 长定子直线电机电磁场有限元分析

1.2.1 仿真模型建立

由于长定子直线同步电机的横向长度远比气隙大，绕组端部较短，铁心均为叠压结构，因此可以做如下简化假设：

（1）假设长定子直线同步电机磁场沿轴向均匀分布，即电流密度矢量J和磁位矢量A都只有轴向分量（J=Jz，A=Az）；

（2）假设电机本体以外的磁场很弱，可以忽略不计，则电枢和磁极外表面都可近似为一零矢量的等磁位面积，即A=0；

（3）假设导体内的电流均匀分布。

基于以上假设建立的长定子直线同步电机物理仿真模型见图2，其中长定子直线同步电机运行方向为x轴，平行于高速磁浮列车高度的方向为y轴,垂直于xy平面向内为z轴。运行时，长定子铁心按周期性边界处理。

1.2.2 仿真模型激励加载

图2 长定子直线同步电机物理仿真模型Fig. 2 Physical simulation model of the long stator linear synchronous motor

（1）长定子绕组激励。本文选取定子绕组电流有效值为0（空载）和1 500 A（负载）两种工况进行仿真，定子绕组电流为三相对称交流电，如式（1）所示。

式中：ia,ib,ic——定子绕组ABC三相电流；Is——定子线电流有效值；θ——定子与励磁次级相对位置角，即励磁次级的初始位置角；f——定子绕组电流频率。

（2）长定子直线电机稳态激励设置。f被分别设置为10 Hz和100 Hz。由直线同步电机同步速度vs与定子极距τ和电源频率f的关系式（vs=2τf）可以得到，此时磁浮列车稳态运行速度分别为5.16 m/s和51.6m/s。

（3）电磁铁励磁激励。长定子直线同步电机是电励磁直线同步电机，本模型励磁绕组激励采用励磁电流If= 25 A的直流电。

1.2.3 仿真结果分析

基于上述给定条件，经过有限元软件后处理模块得到长定子电枢磁场与电磁铁悬浮磁场在q轴对齐条件下，实现悬浮磁场和牵引磁场解耦的仿真结果：

（1）长定子直线同步电机空载工况下的仿真结果见图3～图6（空载指只有电磁铁有激励且If= 25 A、电枢绕组电流为0的工况）。

图3 长定子直线同步电机空载反电势波形Fig. 3 No-load back EMF waveforms of the long-stator linear synchronous motor

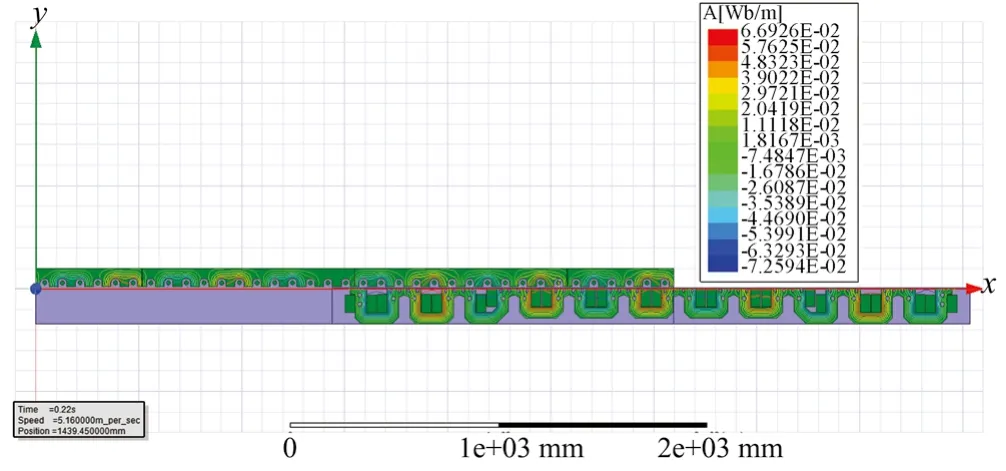
图4 长定子直线同步电机空载磁场分布云图Fig. 4 No-load magnetic field distribution cloud of the long-stator linear synchronous motor

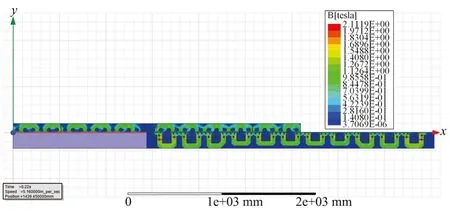
图5 长定子直线同步电机空载磁通密度分布云图Fig. 5 No-load flux density distribution cloud of the long-stator linear synchronous motor

图6 长定子直线同步电机空载气隙磁通密度波形Fig. 6 No-load air gap flux density waveform of the long-stator linear synchronous motor

对图3进行FFT分析，得到长定子直线电机空载反电势线电压峰-峰值（约为495 V）；根据单节车单侧线电压峰-峰值，可计算出空载反电势系数。由图4可知，长定子直线同步电机最大空载磁场强度为6.692 6×10-2Wb/m。由图5可知，长定子直线同步电机最大空载磁通密度约为2 T。由图6可知，空载气隙磁通密度幅值约为0.7 T。因此可得到，长定子直线同步电机各部分磁通密度较高、磁负荷较大。

（2）长定子直线同步电机负载（励磁绕组为25 A，定子绕组供电电流为1 500 A）工况下的仿真结果见图 7～ 图 10。

图7 长定子直线同步电机负载反电势波形Fig. 7 Load back-EMF waveforms of the long-stator linear synchronous motor

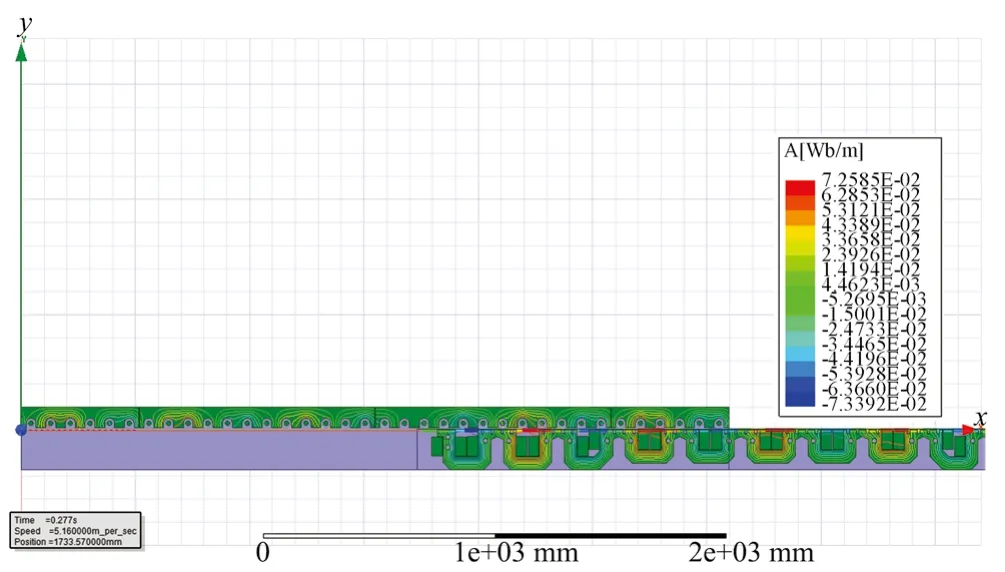
图8 长定子直线同步电机负载磁场分布云图Fig. 8 Load magnetic field distribution cloud of the long-stator linear synchronous motor

图9 长定子直线同步电机负载磁通密度分布云图Fig. 9 Load flux density distribution cloud of the long-stator linear synchronous motor

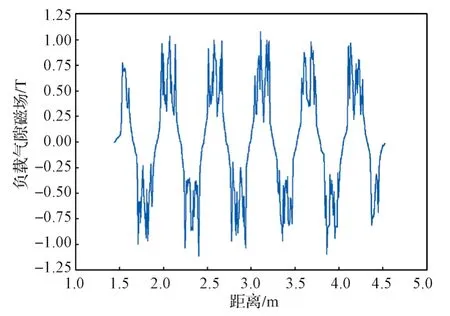
图10 长定子直线同步电机负载气隙磁通密度波形Fig. 10 Load air gap flux density waveform of the long-stator linear synchronous motor

对图7进行FFT分析，得到长定子直线电机空载反电势线电压峰-峰值约为500 V。由图8～图10可知，长定子直线同步电机最大空载磁场强度为7.258 5×10-2Wb/m；长定子直线同步电机最大负载磁通密度约为2 T，负载气隙磁通密度幅值约为0.8 T。

通过对长定子直线电机空载和负载两种工况最大磁通密度和气隙磁通密度的计算结果进行对比分析，可以得出结论：长定子直线同步电机的励磁绕组是建立气隙磁场的主要因素。

2 长定子直线同步电机电磁力分析

长定子直线同步电机的电磁推力和法向力被分别作为高速磁浮列车运行的直接牵引动力和悬浮支撑力的来源，其是高速磁浮列车平稳运行的根本保证。本节通过有限元电磁力计算方法，分别对长定子直线同步电机励磁绕组在有激励和无激励两种工况下，加载相同定子绕组电流（1 500 A）及不同相位角θ时的电磁力进行计算。

2.1 电机有限元电磁力计算理论

直线电机电磁力是直线同步电机非常重要的性能参数。在电磁场理论中，计算电磁力的基本方法有麦克斯韦应力张量法和虚位移法。

2.1.1 麦克斯韦应力张量法[9]

根据麦克斯韦理论，可以把作用在介质任意区域上的体积力归为这个区域表面S所受到的张力。若两种介质的磁导率分别为μa和μb，则在磁场中作用于物体表面上的力可被表示为

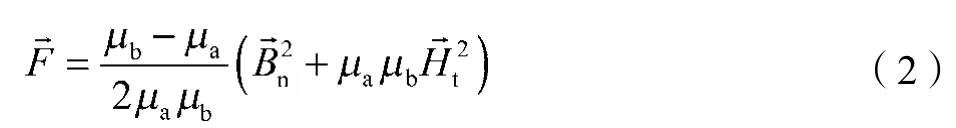
式中：Bn——磁通密度在S平面的法向量；Ht——磁场强度在S平面的切向分量；力F的方向由磁导率大的介质指向磁导率小的介质。

当两种介质分别是铁磁材料与空气时，力的计算表达式为

式中：μ1——铁磁材料磁导率；μ0——空气磁导率；μr——铁磁材料相对空气磁导率；F的方向总是由铁心指向空气。

2.1.2 虚位移法[9]

虚位移法是基于能量守恒原理与虚位移原理的一种计算电磁力方法。当电磁装置的某一部分发生微小位移时，若在恒电流或恒磁链的条件下，整个系统的磁能会随之变化，则该部分就会产生电磁力，且电磁力的大小等于单位微增位移时磁共能的增量(电流约束为常量)或单位微增位移时磁能的增量(磁链约束为常量)。当用有限元方法计算并假设磁链约束为常量时，采用矢量磁势计算比较方便。磁场中物体所受力可被表示为

式中：Fk——磁场力；Wm——磁场储能；ψ——磁链；x——位移；xk——虚位移。

本文基于上述长定子直线同步电机二维模型和电磁力计算理论，采用有限元仿真软件进行长定子电枢磁场与电磁铁悬浮磁场解耦情况下的牵引力和悬浮力的仿真计算。

2.2 长定子直线电机电磁力仿真结果

2.2.1 电磁牵引力有限元计算

在不忽略定子和磁极铁心损耗的条件下，按不同的定子电流相位角θ给定长定子绕组激励，经有限元法电磁场仿真计算，得到长定子直线同步电机电磁牵引力Fx的力族时序（图11）；对图11进行后处理，得到电磁牵引力Fx与定子绕组电流相位角θ的关系曲线（图12）。

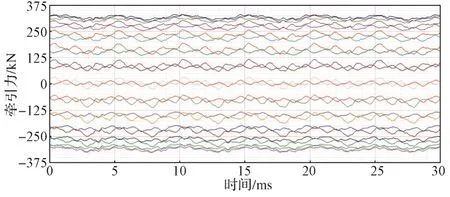
图11 If = 25 A时长定子直线同步电机电磁牵引力时序图Fig. 11 Traction force timing diagram of the long-stator linear synchronous motor as If = 25 A

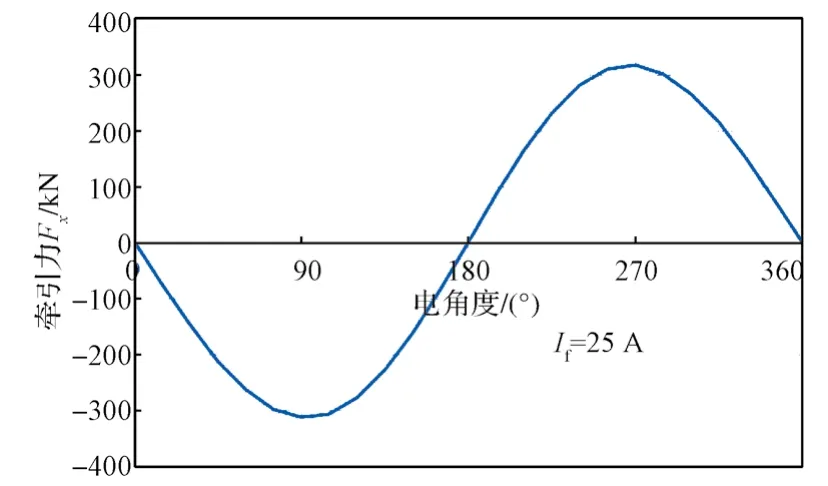
图12 牵引力Fx幅值与电流相位角θ的关系曲线Fig. 12 Relationship between Fx amplitude and current phase angle θ

由图12可知，在长定子直线同步电机励磁激励和绕组激励不变的情况下，三相绕组电流相位角约为90°时，输出电磁牵引力最大，约为310 kN；三相绕组电流相位角约为180°时，输出电磁牵引力最小，且为0。

2.2.2 长定子直线电机悬浮力计算

（1）励磁电流If= 0时悬浮力计算。在不忽略定子和磁极铁心损耗的条件下，按不同的定子电流相位角θ给定长定子绕组激励,且定子绕组电流激励均为1 500 A。经有限元法电磁场仿真计算，得到的长定子直线同步电机悬浮力Fy的力族时序如图13所示。

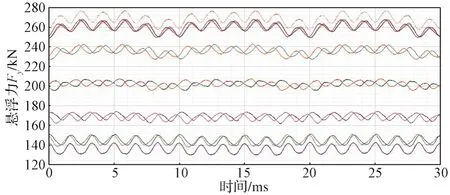
图13 If=0时长定子直线同步电机悬浮力时序Fig. 13 Suspension force timing diagram of the long-stator linear synchronous motor as If = 0

对图13进行后处理，得到悬浮力Fy与定子绕组电流相位角θ的关系曲线（图14）。

图14 电磁悬浮力Fy幅值与电流相位角θ的关系曲线Fig. 14 Relationship between suspension force Fy amplitude and current phase angle θ

由图14可知，在长定子直线同步电机励磁激励为0和绕组激励不变的情况下，三相绕组电流相位角约为90°时，悬浮力最小，约为140 kN；三相绕组电流相位角约为180°时，悬浮力最大，约为260 kN。

（2）励磁电流If= 25 A时的悬浮力计算。计算条件如上并且定子绕组激励为1 500 A时，经有限元法电磁场仿真计算，得到长定子直线同步电机悬浮力Fy的力族时序（图15）。

图15 If=25 A时长定子直线同步电机悬浮力时序图Fig. 15 Suspension force timing diagram of the long-stator linear synchronous motor as If = 25 A

对图15进行后处理，得到悬浮力Fy与定子绕组电流相位角θ的关系曲线（图16）。

图16 电磁悬浮力Fy幅值与电流相位角θ关系曲线Fig. 16 Relationship between suspension force Fy amplitude and current phase angle θ

由图16可知，在长定子直线同步电机励磁激励为25 A和绕组激励不变的工况下，三相绕组电流相位角约为90°时，悬浮力最小,约为4 000 kN。与图14的140 kN相比，可以知道，电磁铁的悬浮电磁场对于悬浮力起主导作用。因此，悬浮电磁场与牵引电磁场q轴对齐时，达到了解耦控制目的，这为长定子直线同步电机的牵引控制提供了理论依据，此时长定子直线同步电机解耦矢量分析如图17所示。

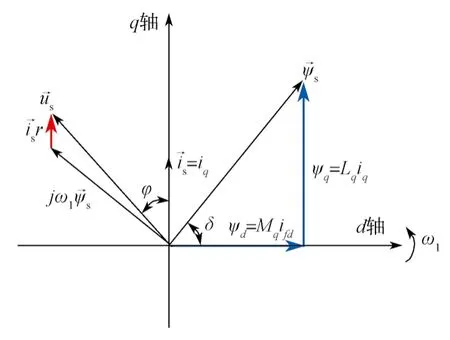
图17 长定子直线同步电机解耦控制矢量分析图Fig. 17 Decoupling control vector analysis diagram of the long stator linear synchronous motor

3 结语

本文基于有限元方法，利用ANSYS有限元软件，首先建立一个标准磁浮长定子直线同步电机的有限元仿真模型，分析了高速磁浮列车用长定子直线同步电机内的磁场分布及其特点；并且应用麦克斯韦应力张量法和虚位移法原理，计算了励磁电流为25 A、定子绕组激励为1 500 A时电磁牵引力和悬浮力特性，以及励磁电流为0、定子绕组激励为1 500 A工况下的悬浮力特性。

经过上述仿真计算分析可知：（1）长定子直线同步电机空载反电势系数线电压峰-峰值为9.59 V/(m/s)，与实际设计峰-峰值10.7 V/(m/s)的计算误差为10.2%，在工程设计允许误差范围之内，说明计算方法正确；（2）长定子直线同步电机的励磁绕组是建立气隙磁场的主要因素；（3）电磁铁的悬浮电磁场对于悬浮力起主导作用。因此，采用悬浮电磁场与牵引电磁场q轴对齐的控制策略可以达到两个磁场解耦控制互不干扰的目的，此结论可为高速磁浮列车用长定子直线同步电机工程应用的设计、优化以及牵引力和悬浮力的控制和改善提供理论参考。