一种线损最小的能馈电压阈值动态调整算法

2020-11-30李红波郑财晖黄子昊罗文广刘华东

控制与信息技术 2020年5期

张超，李红波，郑财晖，黄子昊，罗文广，刘华东

（1. 中车株洲电力机车研究所有限公司，湖南株洲 412001；2. 中车长春轨道客车股份有限公司，吉林长春 130062）

0 引言

城市轨道交通绿色环保、运输能力强大，可以有效缓解城市的环境污染和交通拥堵问题，近年来得到了迅速发展，已成为城市用电大户。目前在轨道交通行业，节能意识已被提升到了新的高度[1]，利用相关技术手段降低轨道交通的能耗已然成为行业研究热点[2-5]，但多以列车再生制动能量的回收利用作为轨道交通节能研究的一个重点，如再生制动能量的回收利用大多以列车为优化控制对象，少有利用地面装置实施优化控制的。随着地面可控设备技术的飞速发展，利用地面可控设备实施优化控制的节能降耗方法将是一种新的技术方向。

在轨道交通的地面可控设备中，再生制动能量回馈装置（简称“能馈装置”）可以回收列车制动能量并将其反馈到牵引电网。相比再生制动电阻器，能馈装置提高了再生制动能量的利用率，有效减少了列车牵引系统用电总量。能馈装置实时监测直流牵引网电压，当列车制动导致牵引网电压超过电压阈值时，其将制动能量回馈到交流牵引电网，以稳定直流牵引网电压，限制列车电压，使之不超过限定值，从而保证列车安全[6]。然而，一方面，因为不同地铁线路牵引电网、钢轨及变电站参数存在差异，现有能馈装置电压阈值的调试工作需要大量的现场人员来完成，人力成本较高；另一方面，因能馈装置电压阈值的大小直接影响列车制动能量的泄放程度以及网络损耗的大小，其目前往往依赖人工经验进行设置，过高的启动门槛会导致列车电压越限，而过低的电压阈值则会致使制动能量利用不充分。因此，本文将能馈装置作为控制对象，以供电区间内线损最小为目标，提出了一种能馈电压阈值的自适应算法，其能根据网络实际情况实时动态调整能馈电压阈值，这对提高轨道交通牵引电力系统的能量利用率、节约现场调试人力成本具有重要意义。

1 网对轨电压潮流算法

在轨道交通牵引供电系统中，能馈装置控制的输出电压为牵引网对钢轨的电压差，而以牵引电网上电位和钢轨上电位为状态量的传统潮流算法[7]因状态量的差异难以被直接应用于牵引供电系统中能馈装置阈值的优化。为此，本文借鉴文献[8]中网对轨电压算法对能馈装置电压阈值进行分析。

潮流计算中钢轨通常采用Π型模型，而流入到排流网或金属导体的电流往往很小，如果忽略此电流，直流牵引网侧的简易等效模型则如图1所示。图中，φ表示电位，Req和Vs分别为牵引变电所等效电阻和电压，R1，R3，R5和R7为牵引网网上电阻，R2，R4，R6和R8为钢轨电阻，It为列车电流。

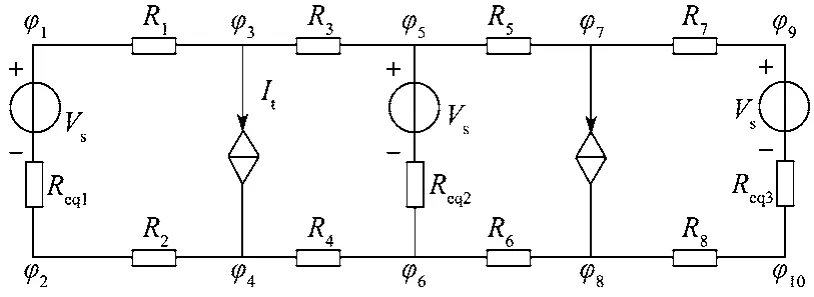
图1 直流牵引供电系统等效模型Fig. 1 Equivalent model for DC traction power supply system

由于忽略了流入到排流网或金属导体的电流，因而牵引网上电流等于钢轨回流电流：

其他供电区间同样存在类似式（1）的关系。

将式（1）左边分子分母同乘(R1+R2)，化简后可得

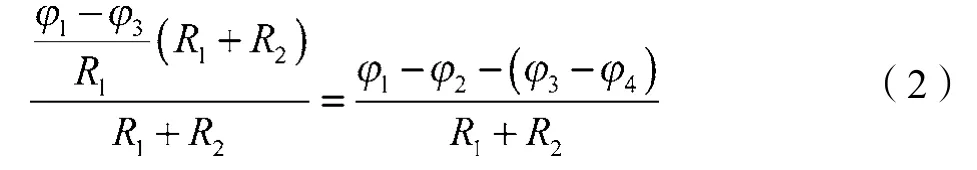
同理也存在

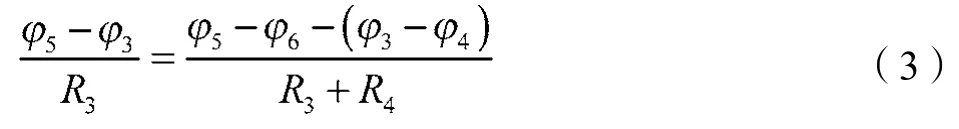
基于牵引电网和钢轨电位，图1中节点1和节点3的节点电压方程为

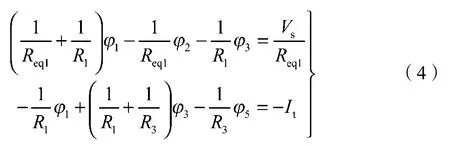
令φ1-φ2=U1，φ3-φ4=U2，φ5-φ6=U3，基于式（2）和式（3），可将式（4）改写为

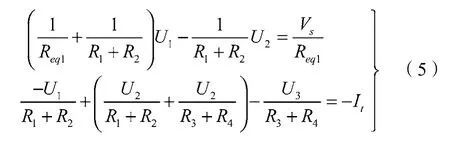
式（5）表明，钢轨电阻转移至牵引电网后，网对轨的电压差（U1,U2和U3）具有类似传统节点电位方程的形式。结合图1，式（5）可用图2的等效电路描述其连接关系。

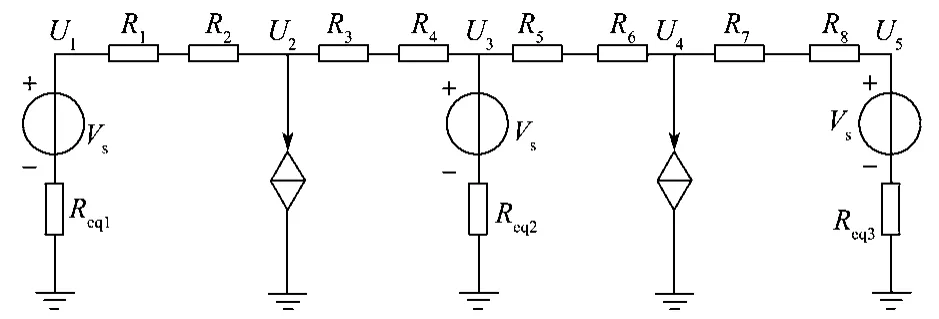
图2 网对轨电压算法的等效电路Fig. 2 Equivalent model of catenary to rail voltage

图2中，U1和U2之间的电流为

式（6）说明，采用电压计算电流和采用电位计算电流，两者形式虽不同，但结果一致，无非是等效电路中钢轨电阻被转移至牵引电网上。

经网对轨电压算法的推导，节点电位方程被转化为节点电压方程，实现了状态量由节点电位到输出电压的转化。

2 线损最小的能馈电压阈值动态调整策略

利用上述转变后的节点电压方程，本文将利用列车信息和牵引变电所内采集的信息构建关于能馈电压阈值的优化模型，并将其转化为椭圆和直线的位置关系进行求解。

2.1 列车信息

列车信息包括电压、电流和功率，是线损优化模型的重要数据。因目前的车地通信系统往往存在数据滞后或通信链路不通的情况(不同设备来源于多个竞争厂商，出于技术保护的目的往往难以实现数据的共享；且由于车地通信的中间环节过多，导致列车数据滞后性非常严重)，地面可控设备想直接利用列车信息进行优化调度几乎不可能，为此，本节介绍列车信息间接获取的方式。

采集图3的I1,I2,U1和U3（其中电流通过直流断路器获取，电压通过牵引所的直流母线传感器获取），根据欧姆定律可得

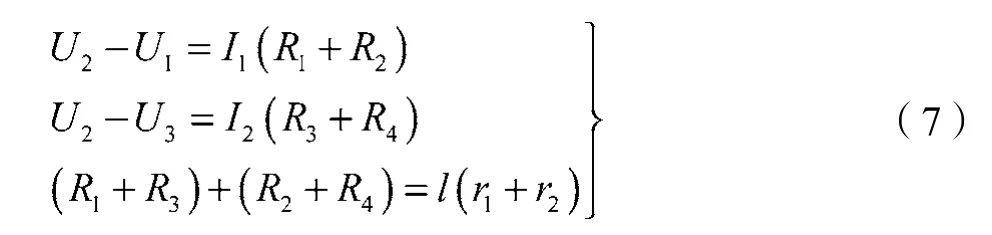
式中：l——两牵引变电所之间的距离；r1——接触网单位电阻；r2——钢轨的单位电阻。

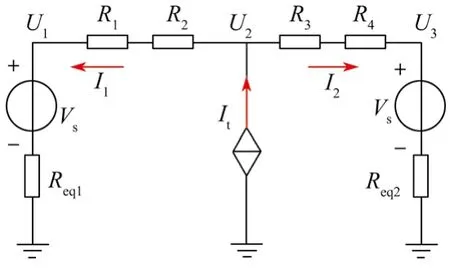
图3 列车及牵引变电所等效电路Fig. 3 Equivalent drawing for the train and traction substations

求解式（7）可得

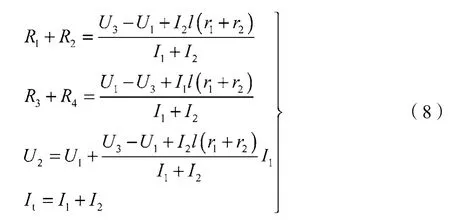
通过式（8）即可获得用于构建能馈电压阈值优化模型的列车信息。虽然式（8）只是单向单一供电区间获取列车信息的方法，但为避免列车排布过密或过稀，并实现能量的高效利用，实际设计列车运行图时通常要求每一时刻上行或下行的每一供电区间内仅有一列车通过，因而式（8）所述列车信息获取方法完全符合实际要求。

2.2 线损优化模型及能馈电压阈值求解

列车制动时，其能量将涌向两侧牵引变电所；随着牵引电网电压的升高，两侧能馈装置将启动并维持牵引变电所输出电压恒定。能馈电压阈值合适与否对网络线损影响较大，为此，本文对单一供电区间的有功线损值Ploss进行分析，并以图3为例给出优化模型：

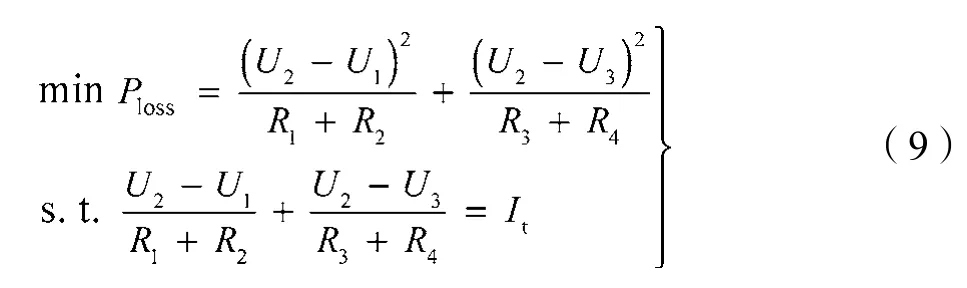
根据式（8）可计算出列车电压、电流和列车至牵引变电所的电阻，即U2,It,R1,R2,R3和R4均为已知量。由于列车制动能量会导致两侧能馈装置启动，同时考虑到启动前后时刻网络状态变化不大，因此利用当前时刻已知的数据计算优化控制变量U1和U3。为分析方便，令x=U2-U1，y=U2-U3，Ra=R1+R2，Rb=R3+R4，则式（9）可改写为

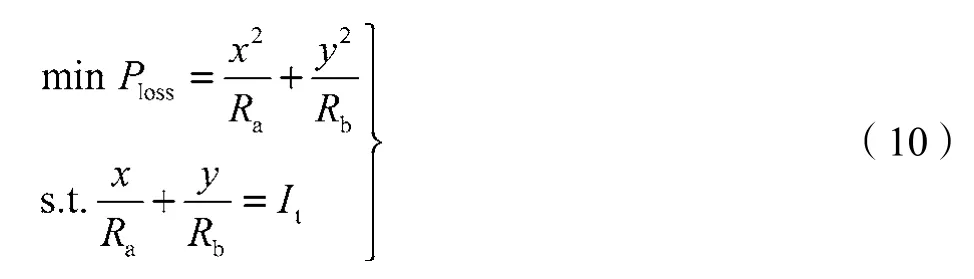
根据式（10）可求得满足约束条件下使得Ploss最小的x和y值。式（10）的目标函数为一椭圆（即Ra≠Rb），约束条件为一条直线，所求得的x和y必须同时在椭圆和直线上，从而将优化问题转为研究直线和椭圆的相对位置问题，如图4所示。由于Ploss决定了椭圆的长轴和短轴，想要Ploss小，应使得椭圆的长轴或短轴小。考虑到直线位置固定且x和y构成的二维坐标点必须在直线上，所以仅当椭圆和直线相切时，才能得到既满足直线约束条件又是最小椭圆的x和y值。

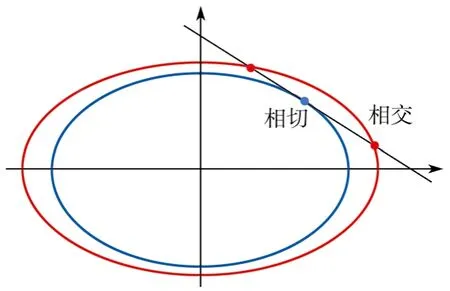
图4 优化模型的几何表示Fig. 4 Geometric representation of the optimized model

化简式（10）中直线和椭圆方程，可得二次方程：

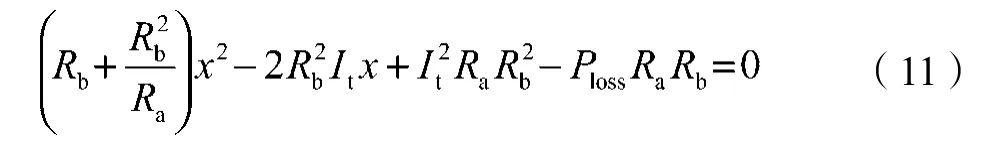
二次方程的判别式Δ和解x分别为

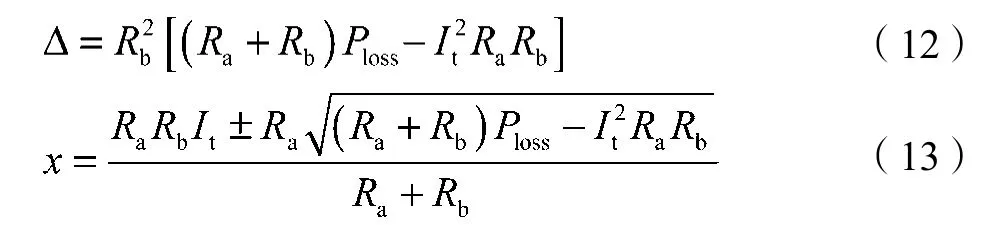
当直线与椭圆相切时，Δ=0，此时对应的解为

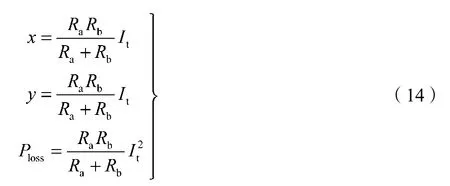
利用式（14）计算电压差x和y，再结合列车电压U2，即可获取两侧能馈装置的电压阈值U1和U3。

2.3 上下行和多供电区间的电压统一

基于运行图优化排布，本文只考虑多车在不同供电区间的情况。考虑到同一供电区间内上行和下行网络中可能同时存在制动列车，致使通过2.2节计算得到的两侧牵引变电所能馈电压阈值将不一致；另外，连续两供电区间也可能同时存在制动列车，导致位于中间的牵引变电所计算得到的能馈电压阈值也将不一致。针对这两类情况，本文进行如下处理：

（1）上行、下行网络同时存在制动列车时，先利用上行网络对应供电区间计算得到的能馈电压来计算线路损耗，再利用下行网络对应供电区间计算得到的能馈电压来计算线路损耗，比较两种方式下损耗并选择损耗小者所对应的能馈电压为阈值电压。

（2）若某两个连续区间均存在制动列车，如图5所示，中间牵引变电所的U3，先按第一供电区间信息计算得到，并计算两个供电区间的损耗，然后U3按第二供电区间信息计算，同样计算两个区间损耗，最后中间牵引变电所的能馈阈值电压选择损耗小者所对应的U3。

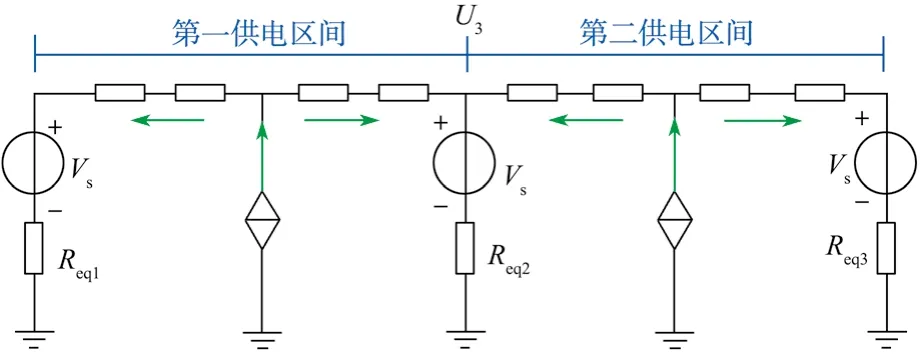
图5 连续供电区间等效电路Fig. 5 Equivalent circuit of consecutive power supply ranges

2.4 能馈电压阈值算法流程

（1）获取牵引变电所输出电压和馈线电流；

（2）以流出直流母线为正、流入直流母线为负分别对上行和下行的每个供电区间进行标记（标记依据是同一供电区间内两侧电流均为负）；

（3）对标记的上行和下行供电区间采用2.2节方法计算两侧牵引变电所的能馈电压阈值；

（4）采用2.3节调整策略统一上、下行网络或者连续供电区间内的能馈电压阈值；

（5）若第（4）步中计算所得能馈电压阈值超过正常范围，则不更新，继续采用上一次电压阈值，否则更新能馈电压阈值；

（6）发送电压指令至能馈装置。

3 算例分析

3.1 数据基础

本文采用长沙轨道交通2号线参数进行仿真分析，该线路上8个牵引变电所均配置能馈装置，上行、下行总共有9辆车在运行，其运行图和列车功率曲线如图6所示，其中时间断面编号代表不同时刻。直流牵引供电系统中单位接触网电阻、钢轨电阻和泄漏电阻分别为0.055 12 Ω/km，0.040 00 Ω/km 和 0.067 00 Ω/km。能馈装置额定功率为3.6 MW，启动电压为1 750 V。仿真时，运行工况与运行图一致，但不考虑列车制动电阻。

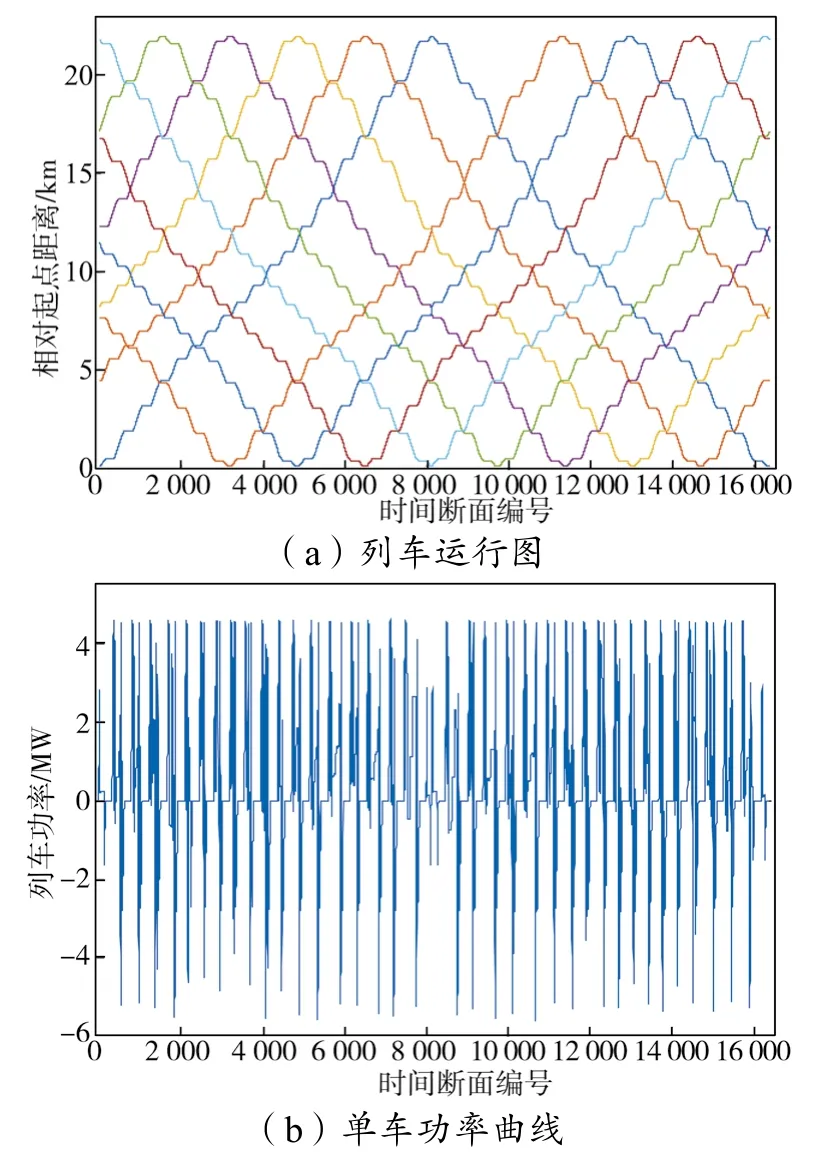
图6 列车运行图和单车功率曲线Fig. 6 Driving profiles and power curve of a train

3.2 网对轨性能分析

图7为采用网对轨电压算法和传统电压算法针对某断面数据的计算结果。从图7可以发现：不同元件电压差异不同，其中牵引变电所的电压波动较小、列车的电压波动较大。用两种潮流算法计算得到的元件电压最大、最小绝对误差分别为4.900 0 V和0.000 5 V，结果表明：利用网对轨算法计算得到的电压误差较小，最大绝对误差未超过1%（4.9/1 500×100%=0.33%），这说明忽略流入到排流网或金属导体的电流并将等效电路中钢轨上电阻转移至牵引电网上的方法是可取的。

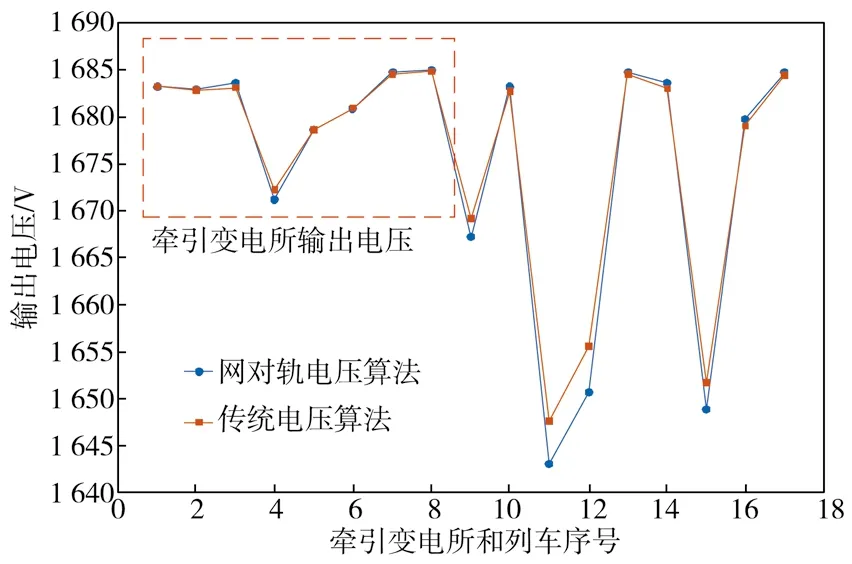
图7 不同算法潮流的仿真结果Fig. 7 Results of different power flow algorithms

3.3 能馈阈值调整策略效果分析

为说明本文所提阈值调整策略的有效性，设置方案A（能馈电压阈值固定为1 750 V）和方案B（本文所提能馈电压阈值动态调整策略）进行对比分析，结果如图8和表1所示。

表1 不同方案的电压差异Tab. 1 Voltage differences of different schemes

从图8可知，采用本文控制方法产生的线损能量节约20.72 kW·h，相对原固定能馈电压阈值方案降低3.21%；另外，由于能馈电压的动态调整，使得网络中制动能量能够被更加充分的吸收或利用，牵引变电所总用电量减小（相比固定能馈电压阈值方案下降0.35%），这表明本文所提方法能够有助于牵引供电系统的节能。

由表1可知，采用固定能馈电压阈值时，列车电压最高为1 947.61 V；而采用本文控制方法时，列车电压最高只有1 921.78 V，下降了25.83 V；同样，采用固定能馈电压阈值时，最大轨电位相比固定电压方案A下降1.11 V。这表明本文所提方法不仅能够实现网络线损能耗的减小，而且有利于对列车最高电压和轨电位的限制。电压的下降主要是因为制动能量通过能馈电压阈值的动态调整被及时调度，不会因接触点能量过度累积而导致列车电压过高。