一种面向中低速磁浮列车的新型速度测量系统及其算法

张征方，蒋 杰，甘韦韦，卢学云，赵旭峰

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

可靠准确的列车速度测量在列车调度安全、列车运行控制中是不可或缺的。磁浮列车作为一种新型的交通工具，有别于传统轮轨式列车，其在运行过程中不依赖传统的轮轨接触，因此无法使用传统轨道交通车辆的旋转测速方法。

目前中低速磁浮列车测速系统主要是基于计数轨枕进行测速定位，该方法在国防科技大学试验线、长沙磁浮快线和北京S1中低速磁浮线上已经得到了应用[1]。虽然此方法具有装置简单、造价低、维护简单及抗干扰能力强等优点，但是存在低速测不准和高速脉冲漏检的问题[2]。因此，很多学者提出了利用加速度信号对低速时的速度进行补偿的方法，以此来提高测速系统的精度和可靠性，但是这些方法对列车线路环境的适应性较差，例如在坡道、弯道工况时计算精度会大打折扣。为此，本文提出一种基于加速度补偿的速度测量系统及其计算方法。其首先利用改进的粒子群算法对模糊系统参数进行最优化搜索，接着将模糊系统用于卡尔曼滤波器中测量噪声参数的自适应调节，最后通过构建模糊规则自适应调整测量噪声矩阵中加速度和速度测量噪声，实现对列车速度的最优估计。

1 新型磁浮车辆测速系统简介

本文所提磁浮车辆测速系统主要包括传感器安装板和测速控制机箱两部分。传感器安装板被安装在车辆底部；在安装板上，以固定间距安装4个电涡流传感器，并通过硬线将信息传输到测速控制机箱中。测速系统的关联关系如图1所示。

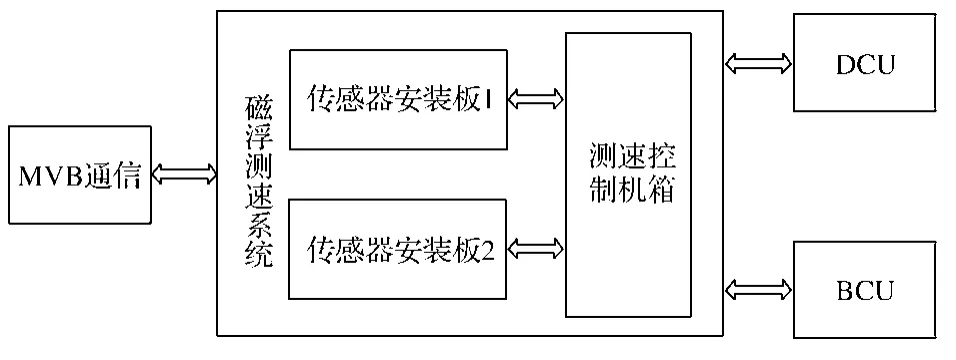
图1 测速系统关联关系Fig. 1 Correlation of the speed measuring system

测速系统控制机箱箱体可被安装在司机室柜体中，其主要由电源板、脉冲输出板、信号采集板、MVB通信板及背板组成，其中信号采集板是实现速度测量的主要载体。信号采集板主要实现对4路电涡流传感器信号的采集和故障处理、加速度信号采集、传感器工作电源提供，并利用本文提出的算法进行估算，输出相应的速度信号及状态信号（图2）。

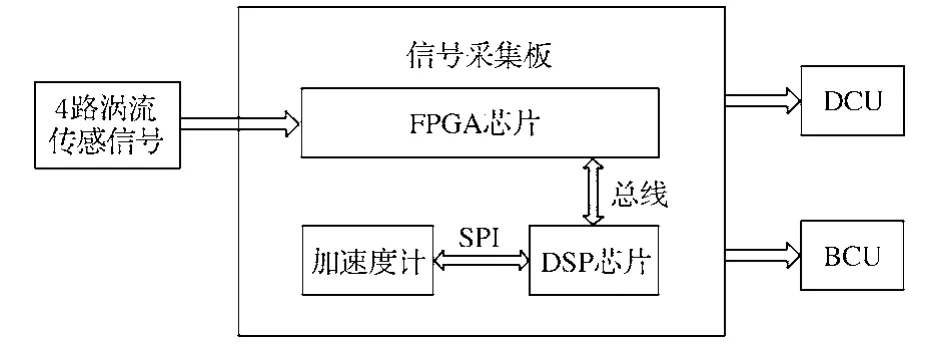
图2 信号采集板原理示意Fig. 2 Schematic diagram of the signal acquisition board

测速系统正常工作时，信号采集板上的FPGA芯片采样4路电涡流传感器信号，通过上升沿的时间差值求其平均值，计算出列车的速度，并通过并行总线将速度计算值传递给DSP，同时DSP通过串行外设接口（serial peripheral interface, SPI）和加速度计进行交互通信，采样列车的加速度信号；DSP芯片通过融合FPGA计算速度和加速度计信号计算出更加精确的列车速度值，并将其传递给FPGA；FPGA通过多功能车辆总线（multifunction vehicle bus, MVB）总线将速度传递到牵引控制单元以及制动控制单元。下文将FPGA通过电涡流传感器信号计算得到的速度称为计数法计算速度，将DSP融合计算的速度称为融合计算速度。

2 本文算法介绍

基于计数轨枕法进行测速定位方法的原理示意如图3所示，电涡流传感器以固定间距(d)被安装在车底，对铺在轨道线路上的金属轨枕进行检测。当以一定速度行驶的列车其电涡流传感器接近轨枕时，传感器将会产生连续的脉冲信号，通过计算脉冲的频率就可以得到列车的速度和相对位移。为提高低速测量准确率并降低高速脉冲漏检率，本文提出一种基于改进粒子群算法的模糊自适应卡尔曼滤波方法。

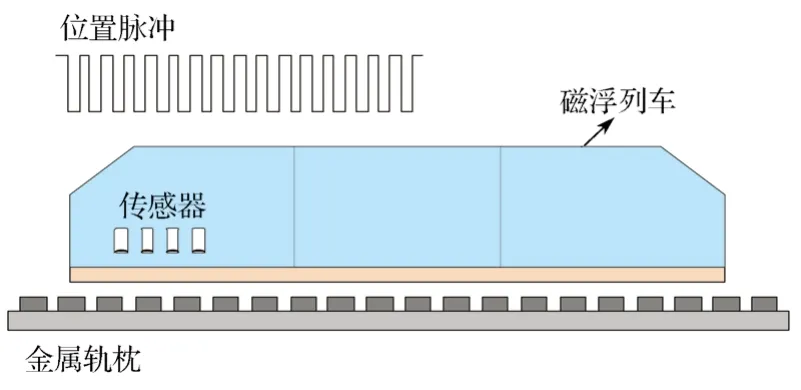
图3 计数轨枕法测速定位示意Fig. 3 Diagram of speed measurement positioning by counting sleeper method

2.1 改进的粒子群算法

粒子群算法是一种最优化理论算法，其将优化问题转化为空间的粒子。粒子有两个重要的参数，即速度和位置，粒子之间通过信息共享的方式使得每个粒子都会朝着当前最优粒子的方向快速移动，最终求得全局的最优解[3]。

假设在一个m维的求解空间中存在有n个粒子，表示为X(X1,X2,…,Xn)，其中第Xi个粒子是一个m维的向量，即Xi=(x1,x2,…,xm)，每一个粒子的运动速度也是一个m维的向量，即Vi=(v1,v2,…,vm)T。传统粒子群算法更新粒子速度和位置的公式如下：

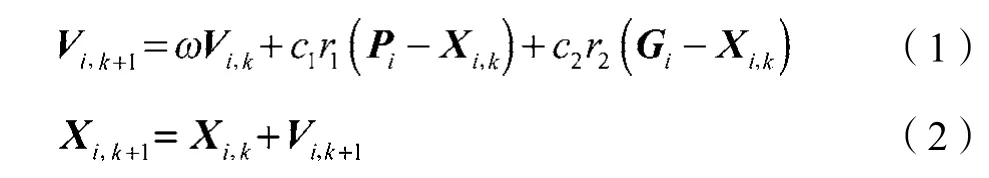
式中：ω——惯性因子；c1,c2——粒子的加速度系数；r1,r2——[0, 1]区间上的随机数；Pi——第i个粒子第k次迭代的最优粒子位置；Gi——第k次迭代的全局最优的粒子位置。

在基本的粒子群算法中，ω取值较小时，其对局部的搜索能力比较强，但是对于新空间的搜索能力较差，因此收敛速度比较慢；当ω取值比较大时，其会提高算法的全局搜索能力，但是有可能会引起振荡而导致无法收敛。针对该问题，本文引用文献[4]中的方法，将速度加权因子和线性递减惯性权重相结合，不断地调整粒子运动速度的大小，以避免传统粒子群算法的易陷入局部搜索空间、易早熟的困境[5]，从而更加智能、准确地寻找空间的最优解。改进后的位置、速度更新公式如下：

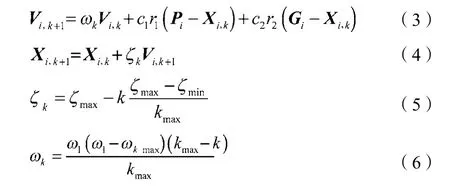
式中：k——迭代次数；kmax—— 最大迭代次数；ζk——第k次迭代的速度加权因子；ζmax——最大速度加权因子；ζmin——最小速度加权因子；ω1——初始惯性因子；ωkmax——迭代到最大次数的惯性因子；ωk——迭代k次的惯性因子。

2.2 卡尔曼滤波

卡尔曼滤波（KF）是一种基于系统的状态空间方程进行时间更新和测量校正的运算方法[6]，其根据当前采样时刻n的估计值Xn预测下一时刻的动态值Xn+1，主要公式如下：

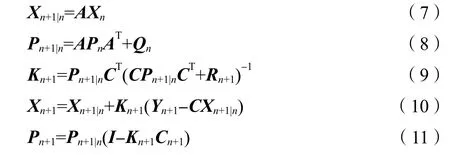
式中：A——系统状态矩阵；C——系统测量矩阵；Xn——第n时刻的状态变量；Yn——第n时刻的输出变量；Q——系统噪声的协方差矩阵；R——测量噪声的协方差矩阵；Xn+1|n——第（n+1）时刻的预测值；Xn+1——第（n+1）时刻的估计值；Pn——第n时刻估算误差的协方差矩阵；Pn+1|n——第n时刻到（n+1）时刻估算误差的协方差矩阵；K——增益矩阵。

本文提出采用卡尔曼滤波对坡道信息以及速度信息同时进行更新。根据车辆运动学理论，当车辆处于坡道运行时，加速度传感器采集得到的纵向加速度不是真实的车辆运动加速度。

式中：a——车辆真实运动加速度；asen——加速度传感器采集加速度；g——重力加速度；α——坡度。

车辆在一个采样周期Δt内，系统的状态方程如下：

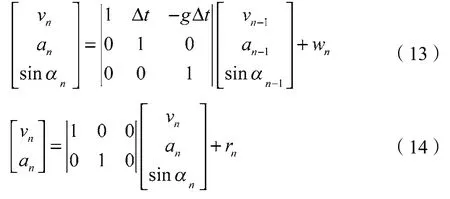
式中：vn——第n时刻车辆速度；an——第n时刻车辆加速度；wn——系统噪声；rn——测量噪声。

2.3 基于改进粒子群的模糊调节器

传统卡尔曼算法存在的主要问题是如何恰当地选取噪声协方差矩阵；而试凑法不仅需要消耗大量的人工精力，而且往往不能找到一个最优的解，已经不能满足当前智能化发展的需求[7]。为此，本文提出一种模糊自适应卡尔曼滤波方法，其通过测量噪声序列方差矩阵R进行实时修正，不仅能智能化地调节，从而更加贴近系统的真实状态，同时也避免了卡尔曼滤波器出现发散现象。

在卡尔曼计算过程中，系统信息为

其理论协方差矩阵为

对应的协方差矩阵方程为

实际协方差矩阵和理论协方差矩阵的差值为

基于改进的粒子群模糊调节器就是根据新息实际协方差矩阵和理论协方差矩阵的差值对模糊系统进行观测噪声的调节。输入Δn的对角元素值Δn(j,j)，输出观测噪声矩阵对角元素的变化量ΔR(j,j)，则定义模糊规则为

该模糊规则中，N, Z, P分别代表偏小、正常、偏大。3个隶属度函数采用高斯型，设其分别为G1(a1,b1) ，G2(a2,b2)，G3(a3,b3)，则模糊系统有9个参数需确定，分别是a1,b1,a2,b2,a3,b3,α,β及γ。 本文利用粒子群算法，将这9个参数作为待优化的变量，所设定目标函数如式（19）所示[8]。利用粒子群算法对模糊参数进行搜索的流程如图4所示。

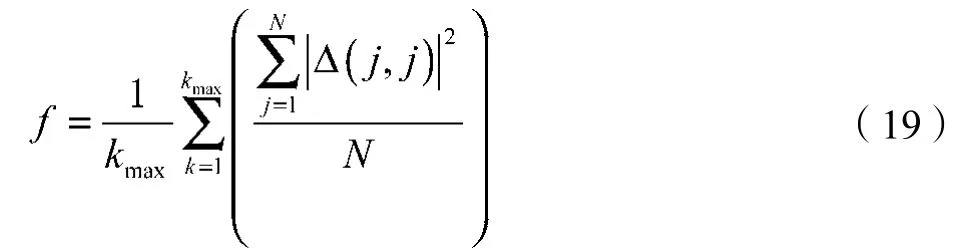
式中：N——Δn(j,j)对角元素的个数，此处N= 2。

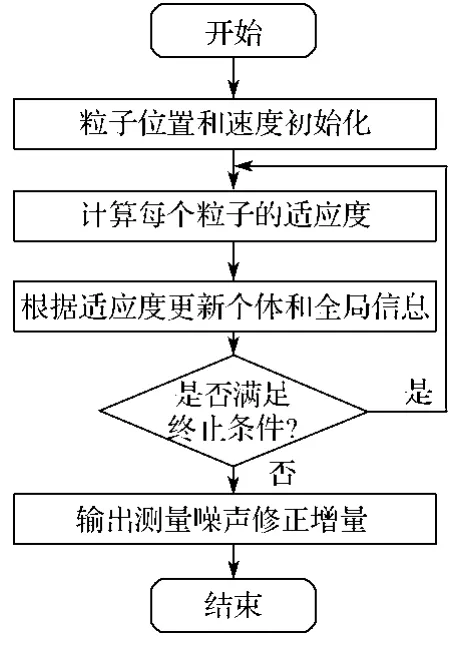
图4 粒子群算法流程Fig. 4 Flow chart of particle swarm optimization algorithm

2.4 本文算法

本文提出的算法流程示意如图5所示。该系统在传统的卡尔曼滤波器的基础上引入了基于改进粒子群的模糊调节器，通过对测量噪声协方差矩阵的实时调整，以改善滤波器的效果，使得融合结果更加贴合真实的情况。

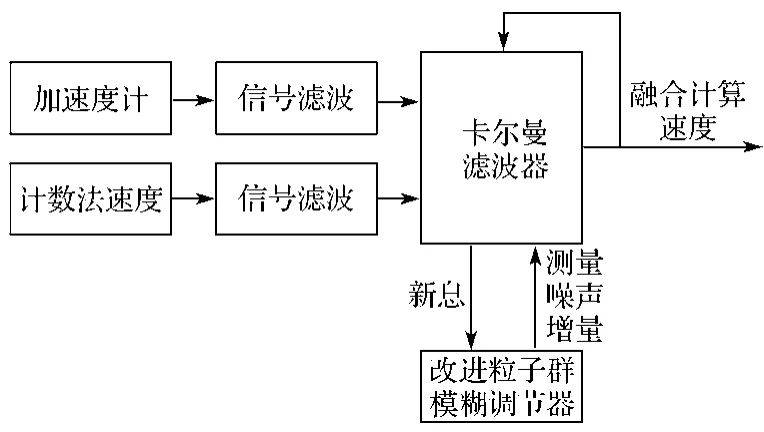
图5 本文算法流程示意Fig. 5 Flow chart of the algorithm

具体实施步骤如下：

（1）分别采样加速度信号和计数轨枕法得到的车辆速度，并对原始信号进行滤波处理；

（2）将滤波后的信号作为卡尔曼滤波器的输入；

（3）改进的粒子群算法根据当前的新息残差训练模糊系统的参数；

（4）模糊系统根据定义的模糊规则输出当前时刻观测噪声的变化量，并输入到卡尔曼滤波器中；

（5）输出最终融合计算的列车速度。

3 现场试验

在某国产中低速磁浮列车上采用ADXL355型3轴MEMS高精度加速度传感器对本文所提速度测量系统及算法进行试验。ADXL355型加速度传感器主要参数如表1所示。实际速度可通过高精度GPS测量装置获取，GPS测量装置采用HWA-PT系列高精度GPS接收机，其速度测量精度可达到0.03 m/s。

表1 ADXL355主要参数Tab.1 Main parameters of ADXL355

3.1 与传统KF算法比较

为了更直观地证明本文所提出算法的有效性，在现场试验采集得到的数据中，将采用本文提出的算法与采用传统的KF算法以及计数法计算得到的速度进行比较，结果如图6所示。可以看出，采用计数法得到的速度在低速阶段存在比较严重的延时现象；采用传统卡尔曼滤波方法得到的速度在人为设定的噪声参数下有突变；而采用本文提出的融合计算方法得到的速度相比于计数法有超前效果，同时比传统卡尔曼滤波方法得到的速度更加平滑。

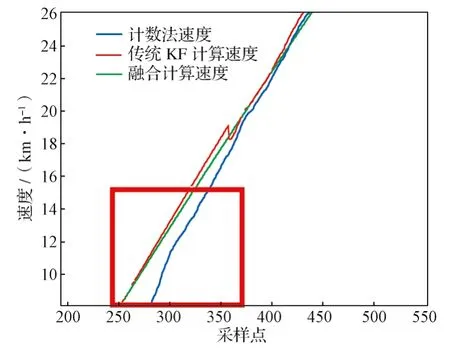
图6 平直道线路计数法速度与实际速度对比Fig. 6 Comparison between speed by straight track line counting method and actual speed

为了评价使用的测量噪声协方差的真实性，本文采用速度方均根误差作为性能指标，在t时刻，速度的方均根误差δ定义如下：

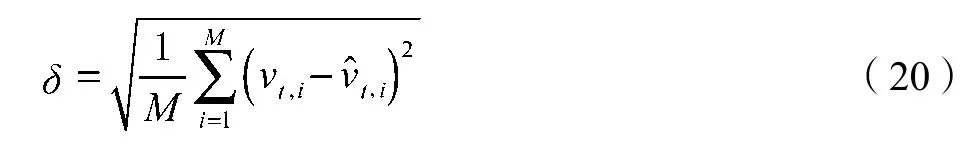
式中：M——试验次数；vt,i和——分别为第i次试验中t时刻的速度真实值和估计值，t=0时刻速度为0，为车辆刚启动阶段。

图7示出真实速度和估计速度的方均根误差。可以看出，初始阶段（即列车刚启动时），方均根误差比较大，即实际速度和估计的速度偏差比较大；100 s时刻以后，方均根误差基本趋于稳定，估计速度更加接近实际速度，表明噪声收敛到了真实值。

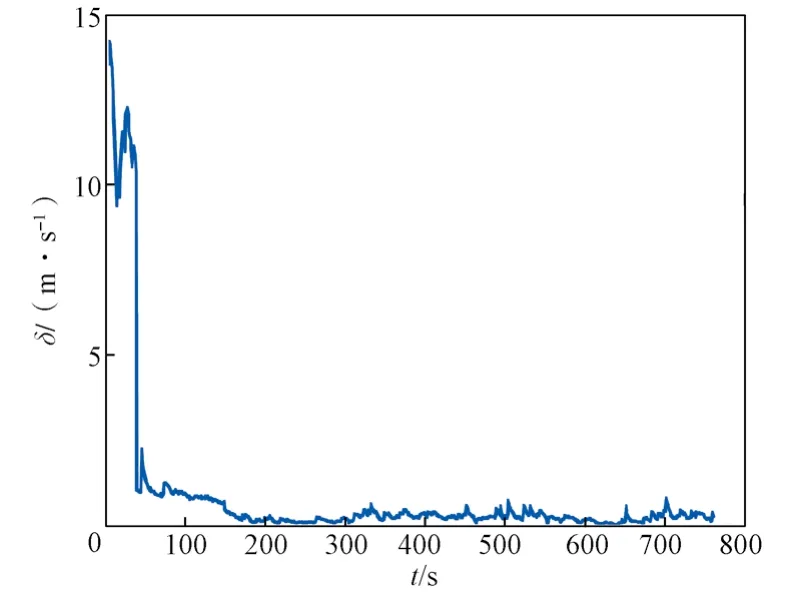
图7 真实速度和估计速度的方均根误差Fig. 7 RMSE of true speed and estimated speed

3.2 平直道试验

车辆在平直道线路上进行试验的数据如图8所示。可以看出，用计数法测量得到的速度在低速阶段存在一定的延时，与车辆真实速度之差超过了1 km/h；且在启动阶段，计数法测得的速度有突变现象，这是因为低速时涡流传感器采样的脉冲更新速度太慢所造成的。

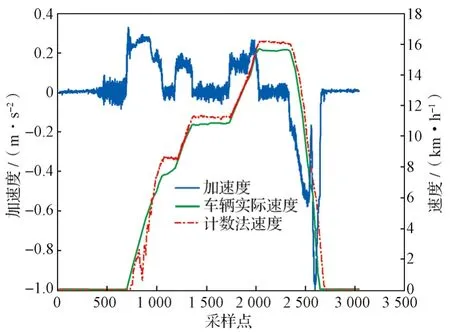
图8 平直道线路计数法速度与实际速度对比Fig. 8 Comparison between speed by line counting sleeper method and actual speed in straight track

图9示出通过本文提出的算法计算得出的车辆速度曲线。从图中局部放大图形可以看出，车辆实际速度和由本文所提方法计算得到的车辆速度基本一致，误差在1 km/h以内。

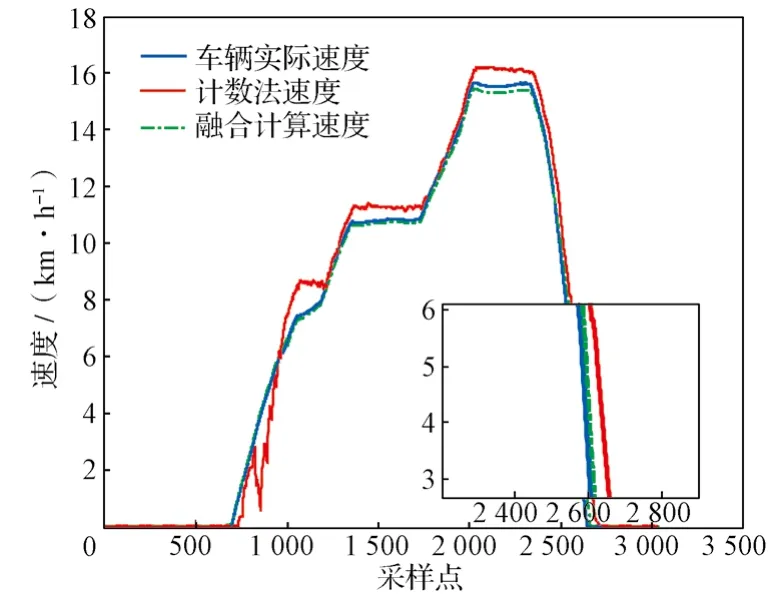
图9 平直道线路融合计算速度与实际速度对比Fig. 9 Comparison between speed by line fusion calculation method and actual speed in straight track

3.3 坡道试验

为了验证本文提出的算法的对于不同路况的适应性，在坡度为52‰的实际坡道上进行了速度测量试验。试验过程为从平直道起车，在下坡道上停车。图10示出用本文方法计算得到的线路坡道角度信息，计算得到的坡度为-2.9°（负号表示为下坡道），换算成坡度约为50‰，与实际坡道信息基本一致。

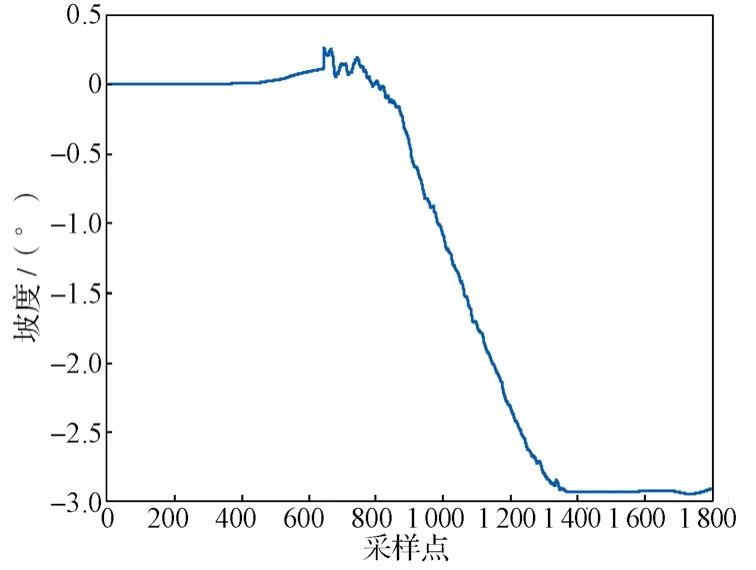
图10 计算线路坡道Fig. 10 Estimated line ramp

图11示出根据测量得到的坡道角度对加速度进行修正的结果。可以看出在下坡的时候，传感器采集得到的原始加速度数值偏大，这将会直接导致计算结果的不准确。

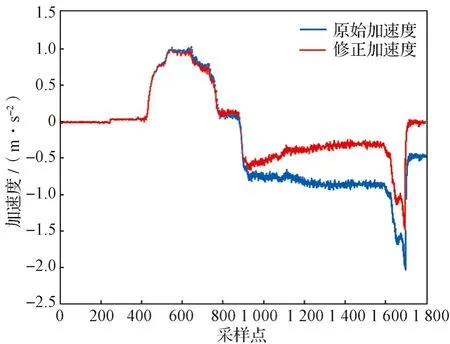
图11 坡道修正前后加速度对比Fig. 11 Comparison of accelerations before and after ramp correction

图12是根据修正后的坡道角度进行融合计算的速度。可以看出，修正后的速度和车辆真实速度基本一致，而计数法得到的速度严重滞后（大约滞后5 km/h）。因此，当电液转换点小于5 km/h时，车辆会容易出现反向牵引的情况；当电液转换点大于5 km/h时，对机械制动的磨损更加严重，不仅会缩短机械制动装置的寿命，而且在低速段利用融合计算得到的速度曲线比利用计数法计算得到的速度曲线更加光滑。

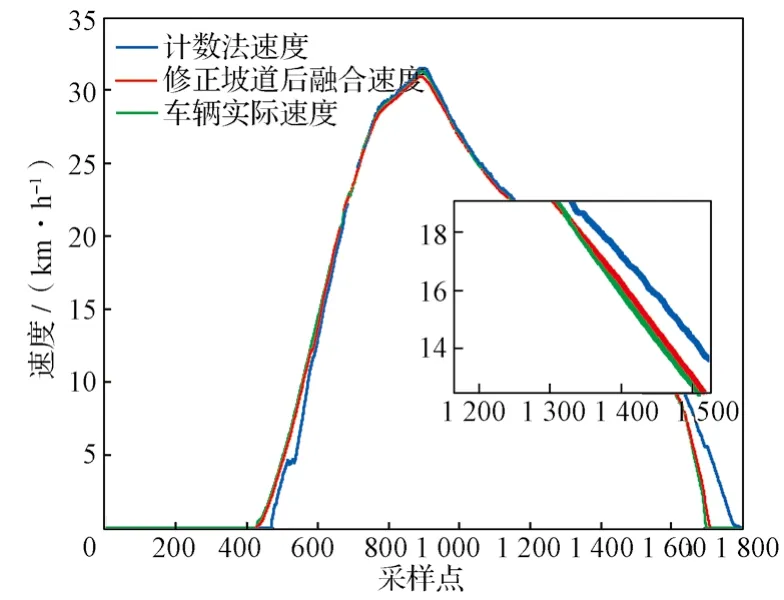
图12 坡道线路融合计算速度与实际速度和计数法速度对比Fig. 12 Contrast of speed by ramp line fusion calculation method with actual speed and speed by counting sleeper method

4 结语

针对磁浮列车计数轨枕法测速存在的不足，本文提出了一种基于加速度补偿的速度测量系统和及其算法。通过在平直道线路和坡道线路进行试验，并与计数法得到的速度相比，表明本文提出的算法可以适应多种路况，计算得到的速度更加贴近于车辆的实际速度（二者误差在1 km/h以内），验证了本文算法的可靠性。相比于传统的卡尔曼估计，本文提出的算法计算得到速度曲线更加平滑，且超前于计数法得到的速度，因此可以指导在列车制动过程中降低电液切换点，更好地利用电制动功能，减少机械制动的使用次数。虽然目前本文提出的测速算法已经通过实际验证，但是对于惯性导航器件测量误差的动态校准以及性能的进一步优化和提升，需要更加准确的测量输入信号，这是下一步的研究方向。