数据驱动下火电机组时延鉴别及主汽温度预测

桂 宁，华菁云

（1.中南大学计算机学院，长沙 410083；2.浙江理工大学信息学院，杭州 310038）

（∗通信作者电子邮箱huajingyun@hotmail.com）

0 引言

火电机组系统相关的预测和控制已经成为一个值得重视的研究领域，火电机组系统是典型的非线性、大滞后、高耦合和复杂的热系统［1］。关键的生产过程指标受到许多因素的影响，往往与其他过程变量之间存在着复杂的非线性关系，其中主汽温度是火电机组最重要的参数之一［2］。主汽温度过高会造成管道和高压缸变形；而温度过低会将水蒸气带入汽轮机，打断和腐蚀低压缸末级的叶片，从而降低机组的效率。因此，准确预测主汽温度对于提高火电机组的运行效率、保证机组的安全运行至关重要［3］。由于火电机组是将燃料的化学能、蒸汽的热势能、机械能分步骤最终转化为电能的复杂过程，各参数之间的关系以及时延现象非常复杂；同时，由于各机组的特性有着较为明显的区别，机组容量越大，时延现象就越严重［4］，很难得到预测对象与各参数之间准确的机理模型的数学表达式［5］。即使通过现场实验的方法得到当时的数学模型，其也会随时间的推移和机组工况的变化发生越来越大的偏差。因此，对于这种复杂系统，必须提供系统性的特征及其时延特性的鉴别方法。此外，特征和时延的判定对于模型的机理分析、模型可解释性均有着重要的意义。

传统的特征选择通常是在质量平衡、能量平衡和动态原理的基础上发展的，这些都高度依赖于专家知识，导致需要较长的建模周期［6-7］。近年来，数据驱动的方法被越来越多的采用，直接分析机组积累的大量历史数据即可提取特征［8］。Buczyński 等［9］通过敏感性分析判断筛选出对CFD（Computational Fluid Dynamics）模型产生实质性影响的特征，用于预测使用固定燃料燃烧的家用中央供暖锅炉的性能；Pisica等［10］选择互信息来评估特征子集相关性，以确定电力系统的运行状态；Wang等［11］利用改进的随机森林的输出作为反向传播神经网络的输入来加权特征的重要性，并提高NOx的预测精度。

上述的工作主要集中在寻找与建模目标参数相关的特征，并未涉及其时延的影响。目前对于特征的时延计算问题较少，Lv 等［12］使用粒子群优化来确定时延，并使用最小二乘支持向量机来预测循环流化床锅炉的床温，然而这种方法在大规模数据集建模时会存在计算复杂性的问题；Shakil 等［13］应用动态神经网络对NOx和O2进行软测量；Xiong等［14］构建了基于局部时延重构的移动窗口时差高斯过程回归方法来动态的计算化学工程中的反应时延的问题，该方法主要通过动态的进行窗口状态匹配的方法来计算时延，特别是动态变化的时延。这些研究主要是通过建模误差反馈的方式对时延进行计算，存在计算量较大的问题。

本文提出利用火电机组DCS（Distributed Control System）中的历史运行数据，根据机组各特征和预测目标的时间和空间维度上的关系进行特征选择和TD-CORT（Temporal Correlation Coefficient-based Time Delay）时延计算。本文算法根据各参数与预测目标主汽温度之间的时延计算结果，重新匹配滑动窗口以重构准确考虑时延特性的建模数据集，然后采用深度神经网络（Deep Neural Network，DNN）与长短期记忆（Long Short-Term Memory，LSTM）模型相结合的融合模型对火电机组30 s 后的主汽温度进行精确建模，实现了从机组的运行参数的变化到机组的物理模型的变化的辨识。该工作已部署应用于国内某1 000 MW 超超临界火电机组，本模型已在前期构建的基于容器的火电机组的边缘计算网关［15］上部署，准确运行了10 个月，为机组的效率提高与安全运行提供了有效的指导。结果表明，该预测系统具有较高的精度，平均绝对误差（Mean Absolute Error，MAE）值达到0.101 6，相较于传统的未考虑时延的深度神经网络的预测MAE值0.238 6，准确度提升了57.42%。

1 特征选择

1.1 火电机组特征的基本说明

常见的火电机组结构如图1 所示，其由多个子系统构成：磨煤机、排粉风机、送风机、空气预热器、锅炉、引风机、除尘器等。在燃料的化学能最终转化为电能的过程中，火电机组部分参数对建模目标有着不同程度和不同时延的影响，影响的差异通常是由各机组的物理模型决定的。

在本文研究的某1 000 MW 超超临界火电机组中，直接传感器的数量高达15 824 个，其采样频率为3 s。火电机组中的检测设备众多且机组产线多，传感器分布非常广，分为总线仪表、功能块、系统点、中间变量以及IO 点特征。根据本文的建模任务，排除总线仪表、功能块、系统点3 个部分的特征，选择更有实际建模价值的中间变量和IO 点部分的特征，其中，中间变量包括DS、AS、DMI、AMI 中的传感器特征，IO 点部分包括DVI、DVO、AVI、AVO、PUI、SOE_DH、REALOUT、REALIN、BITOUT、BITIN 中的传感器特征。在这些特征中，一部分是“COUNTER 计数器”特征，共计588 个，这些特征对预测重要参数是没有实际价值的，因此直接过滤这部分特征。

图1 火电机组结构示意图Fig.1 Schematic diagram of thermal power unit structure

另外，通过统计发现，其中存在一部分特征为恒定值，这部分特征也被认为是对预测重要参数是没有价值的，共计9 711个，过滤后剩余保留的特征量为5 525个。

1.2 数据预处理

1.2.1 缺失值处理

由于火电机组工业生产过程中数据为时间序列连续性数据，正常合理的样本数据被认为应当具有连续性且不会发生突变。因此，对于缺失值，采用前值填充的方式进行数据处理。

1.2.2 异常值处理

在数据采集的过程中，因外界环境变化等非正常生产的影响，采样数据存在异常值。采用3σ准则对异常值进行相关处理。计算σ值：

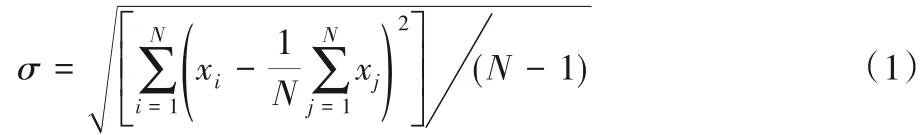
其中xi为x 特征在i 时刻的数值大小。若残差3σ，则xi为异常点，考虑到火电机组流程工业大数据的时序连续性，采用前值对异常值进行替换。

1.2.3 归一化

在本文火电机组建模场景中，采样数据可能会受到离群点的干扰，本文所有特征数据进行零均值规范化（Z-Score Normalization），公式如下：

特征A 的值基于A 的平均值和标准差进行规范化。A 的值vi被规范化为，其中，是特征A的均值，σA是特征A的标准差。这种规范化方式会将原始数据映射到均值为0、标准差为1的分布上。

1.3 结合相关性系数和梯度提升机的特征选择

火电机组数据主要具有三种特性：非线性、高耦合性以及高维性。各传感器数据并非都与建模目标相关，因而必须进行有效的筛选，即特征选择。一般来说，相关性系数是特征选择的主要方法，但是这种特征选择方法一般面临在特征较多的时候性能下降的问题。本文提出通过相关性系数进行粗筛并结合梯度提升机的特征选择方法进行细筛，最终筛选出与建模目标高相关的特征用于后期建模。

1.3.1 基于Spearman的相关度分析

相比于Pearson 相关系数，Spearman 秩相关系数并不依赖数据必须服从正态分布这一假设。因此，对于火电机组实际运行数据而言，Spearman 秩相关系数是一种用来表征特征之间相关性的非常合适的系数。其计算公式如下：

首先，计算各特征两两之间的相关性系数，对冗余特征进行筛除；然后，计算各特征变量与预测目标之间的相关性系数以筛选出高Spearman 秩相关系数的特征，也就是与预测目标相关性较强的特征。

冗余特征筛除 冗余特征是指相互高度相关的特征。在机器学习中，高方差的共线性特征及低可解释性的模型，会严重导致预测模型泛化性差，通过计算两两特征之间的Spearman秩相关系数可对特征进行筛选。本文中将判定为冗余特征的相关性系数阈值设置为0.98，高于此阈值则该组特征被认为互为冗余，只保留其一。筛选掉高于0.98 的高共线性特征后，删除了55.0%的特征，剩余特征数量为2 484。

高相关性的特征选择 在实际建模场景中，通过Spearman 秩相关性系数的特征选择方法，选取与建模目标相关性系数高于相关性系数的较大四等分点的特征作为保留特征。通过该方法，在火电机组的传感器特征中，保留下了585个特征。

1.3.2 基于梯度提升机的特征选择

更精确的特征选择采用梯度提升机（Gradient Boosting Machine，GBM）来进行。使用筛选出的特征组成数据集构造决策树，不出现在树中的特征在此被认为是无关特征，出现在决策树中的特征会有一个相应的重要性指标。重要性指标的绝对值并不那么重要，但其相对值可用于确定与预测目标最相关的特征。借助主成分分析（Principal Component Analysis，PCA）的思路，特征选择最终只保留累计达到某百分比的总重要性的那部分特征，并将其他低重要性特征直接删除。

在保留的585 个特征中，通过基于梯度提升机的特征选择方法，在该特征子集中再次进行筛选，保留特征的累积贡献度阈值选取为99%。为减小每次树模型结果差异的影响，重要性指标取三次梯度提升机训练结果的均值。对应累计贡献度0.99的特征数量为161，因此，最终保留按照特征重要性降序排列的前161个特征作为对预测目标建模的重要特征。

2 基于TD-CORT的时延计算

上述的特征选择本质上是空间维度的建模特征选择，事实上，时间维度的特征选择同样重要。在火电机组中，不同特征对于预测目标还存在着不同的时延特性。火电机组DCS系统采集的传感器数值来自分布全机组不同位置的各个传感器，这些传感器记录下的特征其中一部分的变化可能会在一定时间延迟后反映到预测目标上，而另一部分可能会落后于预测目标变化。为进行空间维度的特征选择（即保留先于预测目标变化的特征而删除落后于预测目标的特征）和重构考虑时延特性的建模数据集，提出了TD-CORT 时延计算算法，对时延进行精确的判断和分析以获得更精准的建模效果。

考虑到各特征和预测目标的时序序列存在趋势性，本文提出了基于一阶时序相关性系数的TD-CORT 算法来量化时序序列之间的相似度以计算传感器特征之间的时滞时间。一阶时序相关性系数的计算公式如下：

其中：XT、YT分别为两段T 长度的时序序列；xt、xt+1分别为XT序列在t、t+1 时刻的数值；yt、yt+1分别为YT序列在t，t+1 时刻的数值。

计算两个时序序列XT、YT之间的CORT(XT，YT)相关性的数值，便可以合理地量化两时序序列之间的相似度。两个时间序列的一阶时序相关性系数CORT(XT，YT)的大小在［-1，1］。当CORT(XT，YT)=1时表示两时序序列之间有类似的趋势，它们会同时上升或下降，并且涨幅和跌幅相同；CORT(XT，YT)数值越接近1，表示两时序序列之间的上升或下降趋势越类似；CORT(XT，YT)=-1 表示两时间序列之间上升或下降的趋势恰好相反；CORT(XT，YT)=0 表示两时间序列之间在单调性方面不存在相关性。

假设在前后K 个数据点范围内计算时延的大小。TDCORT 算法计算特征X 与预测目标Y 之间时延大小的具体步骤如下：

步骤1 取预测目标Y的任意H长度的连续时序序列：

步骤2 取特征X的(2K+1)个H长度的连续时序序列：

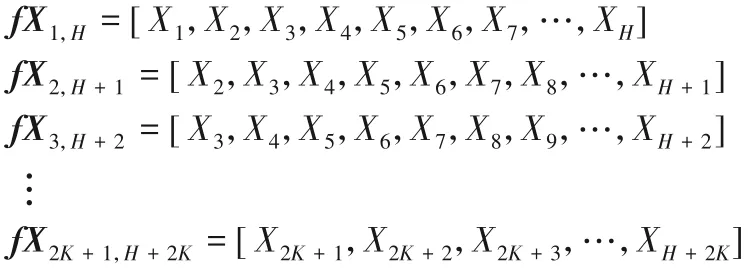
步 骤3 将这(2K+1)个序列fX1，H，fX2，H+1，fX3，H+2，…，fX2K+1，H+2K分别与YK，H+K-1计算(2K+1)次CORT 一阶时序相关性系数，得到一个长度为(2K+1)的特征X 与预测目标Y的CORTX，Y序列：

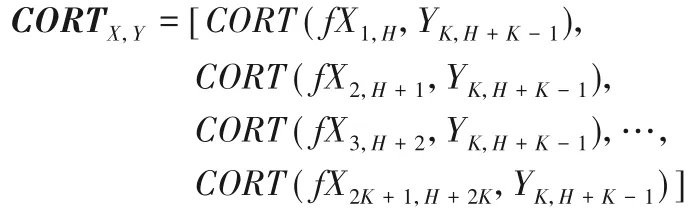
步骤4 将这个长度为(2K+1)的CORTX，Y序列进行五点平滑（构建数据集时滑窗大小也设置为五个点），平滑后的CORTX，Y序列的最大值点对应特征X 与预测目标Y 之间的时延差，即为特征X与预测目标Y之间的时延大小。

构建建模数据集时，使用N 个特征对预测目标（target）进行建模，通过本文提出的TD-CORT 算法获得的N 个特征对于预测目标的时延大小（取绝对值，皆为非负数）分别为d1，d2，…，dN，那么在构建预测模型的输入时，分别以时延dx(x=1，2，…，N)为中心，取滑窗大小为5 个时间点，覆盖尽可能涵盖30 s后预测目标的信息。如当预测t -1时刻后30 s的target时，构建的输入数据即为：

当预测t时刻后30 s的target时，构建的输入的数据即为：

以此类推，这种考虑时延的重构数据集的方法在图2 中详细可视化展示。

3 基于模型融合的建模方法

长短期记忆（LSTM）模型和深度神经网络（DNN）都是目前主流的深度学习模型：LSTM 模型是一种时间递归神经网络，适合进行时间扩展，具有长期记忆功能，适合处理时间序列预测问题，这种预测模型能够具有时间维度的特征表达能力；DNN 模型是具有很多隐藏层的神经网络，是由大量处理单元互联组成的非线性、自适应信息处理系统。相比浅层神经网络，深度神经网络提供了更高的抽象层次，因而能够提高模型的预测能力。

在火电机组的实际建模场景中，不仅需要考虑各传感器参数间空间维度上的关系，还需要考虑各传感器在时间维度上的关系。综合考虑，本文采用LSTM 与DNN 相结合的ensemble 融合模型，抽象出工业大数据在时间维度与空间维度两个维度的特征，从而更好地对目标特征进行建模。融合模型结构示意图如图3 所示，ensemble 模型融合的基本思路是通过对多个单模型融合以提升整体性能。

图3 融合模型结构示意图Fig.3 Schematic diagram of fusion model structure

采用加权模型融合方法，即分别取DNN 与LSTM 预测结果的加权平均进行模型融合，公式如下：其中：n表示单模型的个数，Wi表示第i个单模型权重，predictt表示对应单模型的预测值。本文实验部分具体的融合模型选取LSTM 的模型权重为0.6，DNN 模型的权重为0.4，即n为2，W1为0.6，W2选取0.4。

4 实验与分析

为验证所提出的时延计算方法与融合模型的有效性，在TensorFlow 机器学习平台上进行实验。通过火电机组DCS 系统采集的数据对30 s后的主汽温度进行建模预测。本文的数据来源于某1 000 MW 超超临界发电机组，选取从2018年5月1 日到2018 年7 月31 日三个月的数据作为训练数据，将2018年8月1日至31日一个月的数据作为测试数据。

4.1 时延计算及数据集重构

根据本文提出的TD-CORT 算法，计算各特征对应主汽温度的时延大小。在本文的火电机组工业生产过程中，两个特征之间合理的时延应落在前后3 min 范围内。由于本文数据的采样时间间隔为3 s，前后3 min 范围即前后60 个数据点范围。采用TD-CORT 算法计算时延时，K、L 数值分别设为60、10 000。

图4 展示了主汽温度重要性较高的6 个参数的时延曲线图。图中横轴为时延的大小，从-60到60，虚线为对应时延下该特征的序列与具有30 s时间差的主汽温度序列的一阶时序相关性系数的大小，实线为一阶时序相关性系数的大小的五点平滑后的结果。在每一个曲线图中，五点平滑后的一阶时序相关性都存在一个最大值点，该最大值点对应的时延大小即作为该特征与主汽温度的时延大小。

从图4 可以看出，AM24SIG0304 特征的CORT 最大值为0.682 8，该特征与主汽温度的时延为领先3 个时间点；AM24SIG0601 特征的CORT 最大值为0.393 0，该特征与主汽温度的时延为领先8 个时间点；AM24SIG0307 特征的CORT最大值为0.369 5，该特征与主汽温度的时延为领先33个时间点；HAH51CT255 特征的CORT 最大值为0.315 0，该特征与主汽温度的时延为落后15个时间点；T1AMICVMTMPIN 特征的CORT 最大值为0.196 9，该特征与主汽温度的时延为落后32个时间点；T1AIMSVMTMP 特征的CORT最大值为0.113 0，该特征与主汽温度的时延为落后47个时间点。

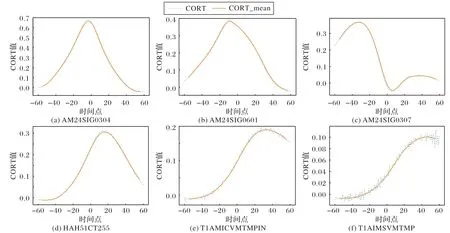
图4 主汽温度权重较高的6个参数时延曲线展示Fig.4 Six parameter delay curves with higher main steam temperature weight

表1 记录了与主汽温度高相关的前6 个特征的时延大小和该时延下对应的CORT 值，其中每个时延时间点为3 s。时延为负数，则说明该特征领先于预测特征变化；时延为正，则说明该特征落后于预测特征变化。落后于预测目标变化的特征，并未对预测目标产生影响，因此直接删除。最终保留所有时延为负的特征，共计57个。

由于在实际问题中，时滞不可能是一个确切的数值，事实上，时延大小会受很多因素影响在一定区间内波动，因此得到的时延大小应该为一个时间窗口，会覆盖在一定波动区间的一个时延范围，因此，在重构考虑时延的数据集时，本文时间窗口取为5个时间点。

表1 与主汽温度高相关的前6个特征的时延大小和该时延下对应的CORT值Tab.1 Time delays of the first six features highly associated with main steam temperature and the corresponding CORT values

4.2 预测建模

LSTM 模型采用节点数为72 的LSTM 单元，再接一个128节点的全连接层，激活函数为ReLU（Rectified Linear Unit），输出层的输出为1维。训练时，batch_size 为10 000，优化器选取Adam，学习率为4E-4。DNN 模型采用7 层全连接网络模型，其中输入层的维度为预测目标对应的特征个数的5 倍（时间滑窗大小设为5）。隐藏层设置为7层，每层神经元个数为64，隐藏层激活函数设置为Sigmoid，输出层的输出为1 维。训练时，层间的dropout 参数设置为0.2，batch_size 大小设置为10 000，优化器选取Adam，学习率设置为2E-3。

融合模型选取LSTM 的模型权重为0.6，DNN 模型的权重为0.4，窗口大小统一设置为5。分别对考虑时延重构后的数据集和未考虑时延重构的数据集进行融合模型建模，并与单一的DNN和LSTM模型在数据集上分别进行对比实验。

传统的主汽温度建模，通过专家知识对机组进行机理分析得出主汽温度容易受到的影响因素。例如，烟气温度的变化、烟气压力的波动、机组负荷的变化、主汽压力的变化、燃料量的变化、给水温度和给水流量的波动、煤水比的变化等都会引起主汽温度的变化［2］。

机组对于火电机组主汽温度一般采用二级减温水结构对末级过热器出口温度进行控制，其中，一级减温水起到粗调作用，二级减温水起到细调作用。因此，本文将一级减温水流量、二级减温水流量的变化也作为影响主汽温度的特征。

传统的建模方式采用以上机理分析得到的相关特征，通过传统线性回归模型对主汽温度进行建模。

为衡量模型性能，本文采用平均绝对误差（MAE）、均方根误差（Root Mean Square Error，RMSE）、平均反切绝对百分比误差（Mean Arctangent Absolute Percentage Error，MAAPE）［16］作为评价指标，计算公式分别如式（6）～（8）所示：

其中：y(t)为真实值，yd(t)为预测值。以上三个指标IMAE、IRMSE、IMAAPE数值越小表明预测值越接近真实值，即模型性能越好。

五种模型在测试集上的预测结果如图5 所示，误差指标的数值结果记录于表2中。

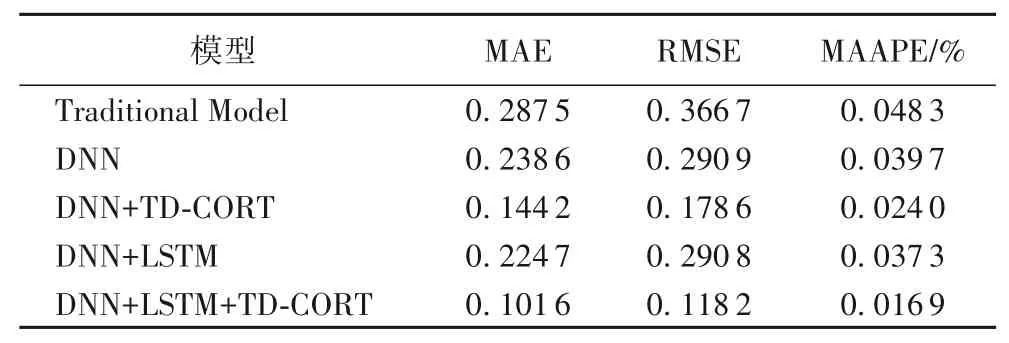
表2 不同模型预测30 s后主汽温度的评价指标值Tab.2 Evaluation index values of main steam temperature after 30 s predicted by different models

观察图5中的预测效果及表2所示的各项模型评价指标，通过比较可以看出本文提出的基于LSTM 和DNN 的融合模型的建模效果都明显优于单一DNN 模型的效果。这组对比，体现了本文提出的LSTM 与DNN 相结合的融合模型的建模有效性。

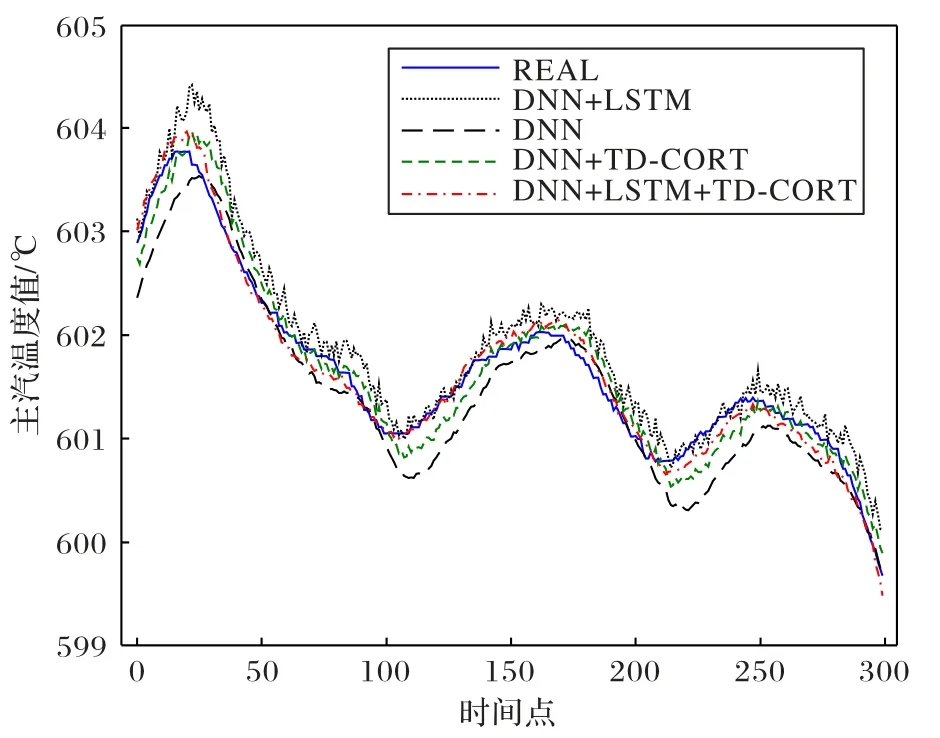
图5 不同模型预测30 s后主汽温度效果对比Fig.5 Effect comparison of different models on the prediction of main steam temperature after 30 s

观察图5 中的预测效果及表2 中对应的各项模型评价指标，通过比较可以看出根据本文提出的基于TD-CORT 计算的特征与预测目标之间的时延构建的模型能够更好地覆盖表征了30 s 后主汽温度变化的信息。考虑特征时延大小，并基于以这个时延大小为中心构建五时间点滑窗的这种构建输入量的方法，建立了更精准的模型输入特征数据集。不论是对于单一DNN 模型而言，还是对于DNN 与LSTM 的融合模型而言，考虑TD-CORT 时延时的建模效果都明显优于未考虑时延时的建模效果。实验充分体现了本文提出的TD-CORT 时延计算方法的有效性，相对于传统的未考虑时延的深度神经网络预测MAE 值为0.238 6，本文的预测结果MAE 值为0.101 6，相较于传统机理分析的线性模型的建模准确度提升了64.66%，相较于未考虑时延的神经网络的模型的预测准确度提升了57.42%。

5 结语

针对数据驱动的工业系统建模面临的特征种类繁多、特征的时延关系复杂带来的建模特征构建复杂、计算量大的问题，提出了一种基于特征关系的时延计算方法，根据数据间关联自动计算特征的时延特性。准确的时延特性构建可以在有限的建模复杂度的情况下，实现模型高精度的预测。在DNN和LSTM 的融合模型上进行了测试，实验结果证明，准确的特征时延鉴别可以最多达到57.42%的精度提升。本方法也可以用在其他模型的建模之上，为其提供延迟窗口自动化鉴别。系统已经在某1 000 MW 机组上实现了部署，在长达10 个月的持续化服务中，对多个运行参数的预测一直保持较高的预测精度，为电厂的实际操作调度提供了有效的指导。