基于哑变量的秦巴山区天然栎类林胸径和树高生长模型研究

闵志强,胡云云,王得军,孙景梅,李宏韬,李卫忠

(1.国家林业和草原局西北调查规划设计院 旱区生态水文与灾害防治国家林业和草原局重点实验室,西安 710048；2.西北农林科技大学 林学院,陕西 杨凌 712100)

立地质量是指特定立地条件下植被的生产潜力,立地质量与树种相关联,并有高低之分[1]。立地质量的主要评价方法有林分因子直接评价法、环境因子间接评价法和两者综合评价方法等[2]。间接评价法一般是通过对优势树高与环境因子的定量分析,计算各立地环境因子对林分生产潜力的贡献,利用立地环境因子来描述立地质量等级[3]。立地环境因子主要分为气候、土壤和地形等3个方面[4],而对栎类影响较大的立地因子主要包括坡向、土层厚度、海拔、坡位、土壤质地等[5-8]。竞争是指两个或多个植物体对同一环境资源和能量在争夺中所发生的相互作用[9]。Staebler[10]首次提出了林木竞争指数。竞争指数作为反应林木间竞争强烈程度的数量指标,其实质是林分中的林木对环境资源的需求与现实生境中林木对环境资源占有量之间的关系[11]。林分竞争指标较密度指标能更好地表示林木间争夺资源(阳光、水分、养分)的关系,而竞争优势木可更好地指示立地的利用潜力[12]。目前,国内外研究提出的林木竞争指标数量较多,大致可分为两大类,即相对型竞争指标与绝对型竞争指标[13]。其中,绝对型竞争指标中的Hegyi竞争指数及其改进型,由于计算简单、容易测量,在竞争指标分析中被广泛使用[14-17]。林分的生长与林分年龄、立地质量、林分密度和经营措施等因子相关,其中,立地质量反映林地的生产潜力,林分密度反映林分对林地的利用程度。作为影响林分生长的两个关键因子,林分密度和立地质量参数在引入到传统林分生长模型后,可以有效提高模型的预测精度和模型的适用性[18-21]。

目前,栎类林在我国分布范围最广、面积最大,其中起源为天然的面积占到88.59%；我国栎类林面积为1 656.26万hm2,蓄积为14.18亿m3[22]。由于栎类资源遭到不同程度破坏,现存栎类天然林大多为残败次生林[23-24]。本文以秦巴山区天然栎类林为研究对象,分析栎树胸径和树高生长规律,建立包含立地质量哑变量和林木竞争哑变量的栎树胸径和树高生长模型,以期为估测栎类林分的生长量和收获量提供基础模型,并为栎类次生林修复和质量精准提升提供重要依据。

1 研究区概况与研究方法

1.1 研究区概况

研究区域主要覆盖秦岭山区和大巴山北坡,总面积近15.42万km2。秦巴山区森林覆盖率53.8%,天然林面积占77%,物种多样性丰富。秦岭有“植物种质基因库”之盛誉,栎树作为当地植被建群树种,一般分布在阳坡或山梁上,主要种类有栓皮栎(Quercusvariabilis)、麻栎(Quercusacutissima)、锐齿槲栎(Quercusalienavar.acuteserrata)、槲栎(Quercusaliena),常形成纯林或混交林,伴生乔木树种有侧柏(Platycladusorientalis)、华山松(PinusarmandiiFranch.)等,灌木有黄刺玫(Rosaxanthina)、栓翅卫矛(Euonymusphellomanus)、鼠李(Rhamnusdavurica)、胡枝子(Lespedezabicolor)等。该地区属北亚热带湿润区,年平均积温为4 500～5 100℃,最冷月平均气温0～4℃,年干燥指数0.050～0.99,日平均气温≥10℃的天数约220～239d。该地区土壤以森林褐色土和黄棕壤为主,植被以亚热带常绿落叶阔叶植物为主。研究区内气温、降水、植被及地貌变化差异不明显,可以利用地形、土壤等因子确定立地主导因子[25]。

1.2 数据来源

数据来源于第八次和第九次全国森林资源连续清查(简称“一类清查”)中的样地调查数据[22]。该数据集中,主要的调查因子包括优势树种、平均胸径、平均树高、地貌、海拔、坡向、坡位、坡度、土壤名称、土壤质地和土层厚度、样地每木检尺数据和空间位置信息数据。本研究中,生长模型拟合样本采用第九次清查数据,生长量相关指标计算采用第八次和第九次两期清查数据。本文选取研究区内一类清查样地共计369块,各样地面积均为666.67m2(1亩)。样地内乔木总株数为11 044株,其中栎木占84.90%,其余树种占15.10%。研究样地的基本情况如表1所示。

表1 样地基本情况Tab.1 Basic characteristics of samples

1.3 研究方法

1.3.1竞争指标

利用全国森林资源连续清查数据中的样木方位角、水平距等信息建立空间位置图,采用Hegyi简单竞争指数为单木竞争指标,其表达式:

(1)

式中:CIi是对象木i的简单竞争指标；Di为对象木的胸径；Dj为对象木周围第j株竞争木的胸径(j=1,2,3,…,n)；DISTij为对象木i与竞争木j之间的距离。

每株对象木相邻的最近4株单木被当做竞争木用以计算简单竞争指数[26]。为了进行样地边缘矫正,本研究采用第4邻体距离判定法消除边缘效应[27]:若样木到第4株相邻木(4株相邻木中的最远邻体)的距离大于样木到标准地4条边的最小垂直距离,则认为该样木可能会受到边界效应的影响,则该样木不作为样地内的对象木,仅作为相邻木参与其他样木的竞争计算。采用样地中所有单木的竞争指数值作为衡量林分水平的竞争指标,根据样地总竞争的数值范围和分布规律,划分林分竞争等级:CI(单木竞争指标和)<250为Ⅰ级,250≤CI≤450为Ⅱ级,CI>450为Ⅲ级。CI越大表示竞争越激烈。CI计算公式:

(2)

式中:CIi是对象木i的简单竞争指数(i=1,2,3,…,n),n为样地内样木总株数。

1.3.2立地质量等级

利用样地数据,提取样地地貌、海拔、坡位、坡度、坡向、土壤类型、土壤质地、土壤厚度、腐殖质厚度等立地因子,采用主成分分析和相关性分析的方法进行因子筛选,删除对评价结果影响较小和信息冗余的因子,最终确定海拔、坡向和土壤厚度为立地质量评价因子。样地中选取竞争指标最小的3株样木代表样地中优势木,并将其年平均生长量作为立地质量分级的依据。对以上3项立地因子进行分级赋分,每项赋分范围为1—5分,以消除量纲的影响,汇总得到立地质量等级。主要评价因子赋分标准如表2所示,按分值划分立地质量等级结果如表3所示。

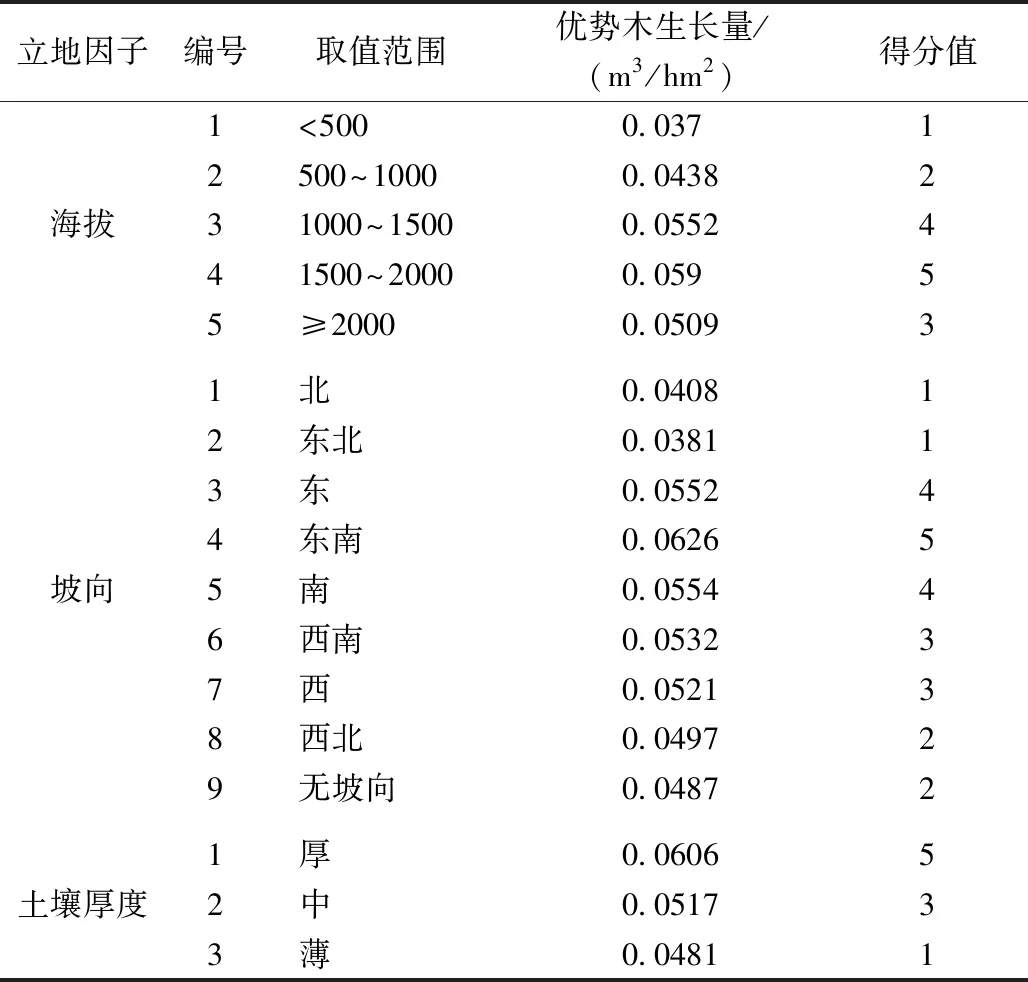
表2 立地因子赋分Tab.2 Site factor assignment

表3 立地质量等级划分表Tab.3 Site quality classification table

1.3.3林分生长模型

借鉴以往研究[18-21],选取常用的林分生长模型(分别为Richards,Gompertz,Logistic和Schumacher模型)进行比选,根据所选4种模型的拟合优度和预估精度筛选出本研究采用的最优基础模型。4种生长模型表达式如表4所示。

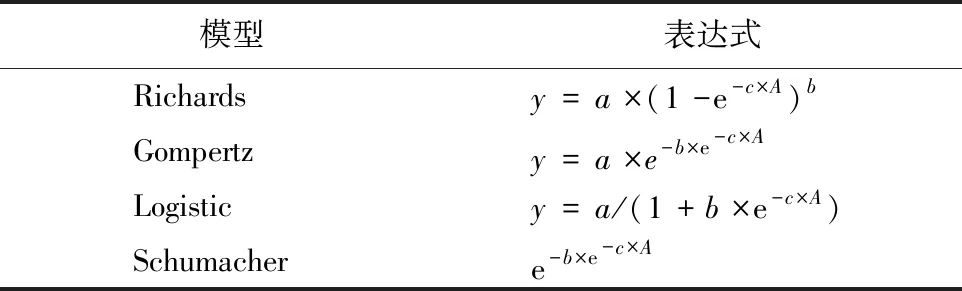
表4 树高和胸径生长模型Tab.4 Growth model of Height and DBH

1.3.4哑变量模型

同一树种的林分生长过程往往受立地条件和竞争状态的共同影响。研究平均树高生长规律时,在基础模型中先引入立地质量等级作为哑变量,确定模型参数形式,再引入竞争等级哑变量来共同构建最优模型。最优模型代表了不同立地条件和竞争状态下的树高生长过程。研究平均胸径生长规律时,由于竞争等级对胸径生长的影响一般大于立地质量等级,因此,先选择竞争等级哑变量确定模型参数形式,再加入立地质量等级哑变量,最终构建胸径生长过程的最优模型。

哑变量,又称虚拟变量[28],它是处理分类变量或定性因子的一种常用方法,哑变量经常取值为0,1,-1。但这些取值并不代表数量的大小,仅仅表示不同的类别[29]。根据立地质量和竞争指标的等级划分结果,以立地质量等级和竞争等级分别作为哑变量,并利用定性代码Si,Sj分别表示不同立地质量等级和竞争等级,将定性数据Si,Sj转化为(0,1),其表达式为:

(3)

式中:i= 1,2,3；j= 1,2,3。

1.3.5模型评价

选取决定系数(R2)和均方根误差(RMSE)对原始模型的拟合优度进行评价,选取预估精度(Pa)和总相对误差(TRE)对原始模型的拟合精度进行评价,选取赤池信息准则(AIC)和贝叶斯信息准则(BIC)对哑变量模型拟合优度进行评价。各评价指标的计算公式为:

(4)

(5)

(6)

(7)

AIC=-2lnl+2k

(8)

BIC=-2lnl+lnn×k

(9)

本研究所有统计分析过程均在SPSS 21.0,Forstat 3.0软件中实现。

2 结果分析

2.1 立地质量等级

根据栎类优势木平均年生长量对立地因子赋分分级,各立地因子的赋分结果如图1所示。结果显示栎木平均年生长量较高的样地主要分布在:1)地貌。海拔1 000～2 000m中山的阳坡。2)地形。平地、平缓的下坡或山谷。3)土壤。腐殖质10～20cm,且土层厚度≥30cm的黄棕壤、黄褐土和褐土,土质以壤土、沙壤土为主。对各立地因子与优势木平均生长量的相关性进行分析,根据相关系数r可以得出,优势木生长受海拔、地貌、坡向等因子影响较大。

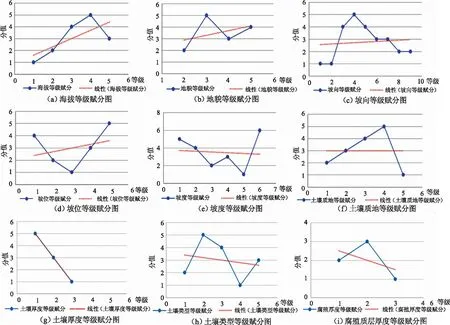
图1 样地各立地因子的赋分结果Fig.1 The scoring results of all site factors for plot

根据9类立地因子进行主成分分析,结果显示主成分特征值大于1的有3个,其中：第一主成分中地貌与海拔因子载荷作用影响明显,认为其代表了地貌有关因子的贡献；第二主成分中土壤类型与土壤厚度的因子载荷值较高,认为其代表了土壤类因子；第三主成分中坡向、坡位和坡度因子载荷值较高,认为其代表了地形类因子。3类主成分代表了影响立地质量的主要类型因子。通过因子双变量的Pearson相关性分析发现,地貌与海拔因子、土壤类型与土壤厚度因子相关程度均为极显著,相关性分别为0.86和0.64,为了消除信息冗余可能带来的影响,选取其中一个因子作为该类型的因子代表。综合以上分析结果,结合栎木生长习性与分布规律等特点,本研究最终选择海拔、坡向和土壤厚度等3个立地因子来划分立地质量等级,具体划分结果如表5所示。

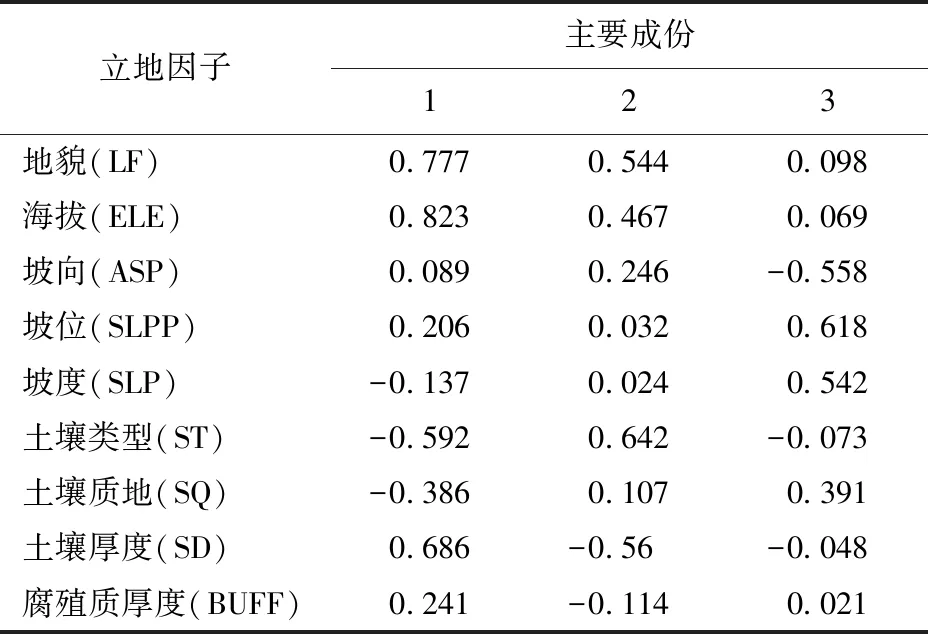
表5 立地因子主成分载荷Tab.5 Principal component load of site factors

2.2 树高和胸径基础模型

分别以胸径(DBH)和树高(H)为因变量,以林龄(A)为自变量,建立生长模型。采用R2,RMSE对模型拟合优度进行评价,以TRE,Pa对模型预估精度进行评价。模型按照R2和Pa值较大,RMSE和TRE较小的原则选取最优基础模型,其中R2为优先评价指标。模型拟合的参数值及评价指标结果如表6所示。

表6 树高和胸径生长模型拟合优度及预测精度Tab.6 Goodness of fit and evaluation accuracy of tree height and diameter at breast height growth model

由表6拟合结果可以看出,树高生长模型中Gompertz模型的R2最高,RMSE最低；胸径生长模型中Gompertz模型的R2和Pa最高,RMSE最低。综合以上结果,确定Gompertz模型作为树高和胸径生长的基础模型。树高和胸径的基础模型结果为:

D=50.12×Exp(-2.14×Exp(-0.0177×A))

(10)

H=21.23×Exp(-1.3662×Exp(-0.0221×A))

(11)

2.3 树高哑变量生长模型

以Gompertz模型为基础,模型所有参数中分别引入立地质量等级作为哑变量,进行树高生长模型拟合。各参数中引入哑变量构建的生长模型拟合效果评价指标结果如表7所示。

表7 立地等级为哑变量的树高生长模型评价指标Tab.7 Evaluation index of tree height growth model with site grade as dummy variable

比较分析不同参数或参数组合构建的哑变量生长模型评价指标,其中参数a,b；a,b,c两种哑变量模型在拟合优度和预估精度方面均优于其它模型,两种模型的R2,Pa相同,RMSE,TRE,SSE值较为相近,但a,b,c参数模型的AIC,BIC值高于a,b参数模型。从简化模型和避免过拟合的角度考虑,选择参数a,b中引入立地质量等级哑变量作为树高生长模型,其表达式为:

现在不少教师一般注重知识的传授和能力的提高，缺乏兴趣激发有效手段，不能调动学生学习。高三学生对生物学习缺乏足够的热情，以为生物只须记忆，学习效果受到极大的影响。生物教师应从学科魅力、生物学独到的研究方法、不断涌现的生物进展、生产生活的密切联系、多媒体教学手段等方面不断暗示学生，激发学生的学习兴趣和学习潜能，以忽略智力的不足。

H=(22.327×S1+19.514×S2+16.059×S3)×Exp((1.2×S1+1.204×S2+1.057×S3)×Exp(-0.023×A))

(12)

与树高基础模型相比,该模型的拟合优度和预估精度均有所提升,决定系数R2为0.717,提高了16.59%；预估精度Pa为98.26,提高了0.65%。

为反映林木竞争对树高生长的影响,在立地质量等级哑变量模型基础上,将竞争等级作为第二类哑变量引入模型中。各参数引入竞争等级哑变量模型拟合效果评价结果如表8所示。

表8 立地等级和竞争等级为哑变量的树高生长模型评价指标Tab.8 Goodness of fit and evaluation index of growth models of H

从表8可以看出,与立地质量等级哑变量树高生长模型相比,所有模型R2,Pa值均上升,RMSE,TRE,SSE,AIC,BIC值均下降,说明引入竞争等级哑变量对树高生长模型拟合优度和预估精度有提升作用。分析不同参数模型拟合效果发现,立地质量等级a,b参数在引入竞争等级a或a,b参数后,R2,Pa相同,RMSE,TRE值较为接近,其中在a,b参数中同时引入立地质量等级和竞争等级作为哑变量时,AIC,BIC值要高于其它参数,为了避免模型参数过于复杂,最终选择立地质量等级在a,b参数,竞争等级在a参数的形式,确定树高生长的哑变量模型,模型表达式如下:

H=(22.08×S11+21.59×S12+18.08×S13+

18.82×S21+18.88×S22+17.94×S23+

16.67×S31+15.78×S32+14.8×S33)×

Exp((1.14×S1+1.17×S2+1.05×S3)×Exp(-0.025×A))

(13)

与立地质量等级哑变量模型相比,同时引入立地质量等级和竞争等级两个哑变量的树高生长模型,决定系数R2为0.745,提高了3.91%；预估精度Pa值为98.35,提高了0.09%。

2.4 胸径哑变量生长模型

由于林木胸径生长过程受林木间竞争影响明显,胸径生长以Gompertz模型为基础,模型参数中先引入竞争等级作为哑变量进行拟合,结果显示,竞争等级哑变量模型的拟合优度和预估精度较基础模型均有明显提升。各参数引入竞争等级哑变量模型拟合效果评价指标结果如表9所示。

从表9可以看出,参数a,c；a,b,c两种哑变量模型在拟合优度和预估精度方面均优于其它模型。a,b,c参数模型虽然在R2,Pa,RMSE,TRE,SSE指标最优,但其AIC,BIC值较高,综合考虑模型简化、过拟合程度影响,最终选择a,c参数模型,拟合决定系数R2为0.834,较基础模型提高13.16%；预估精度Pa值98.17,较基础模型提高0.59%。模型结果为：

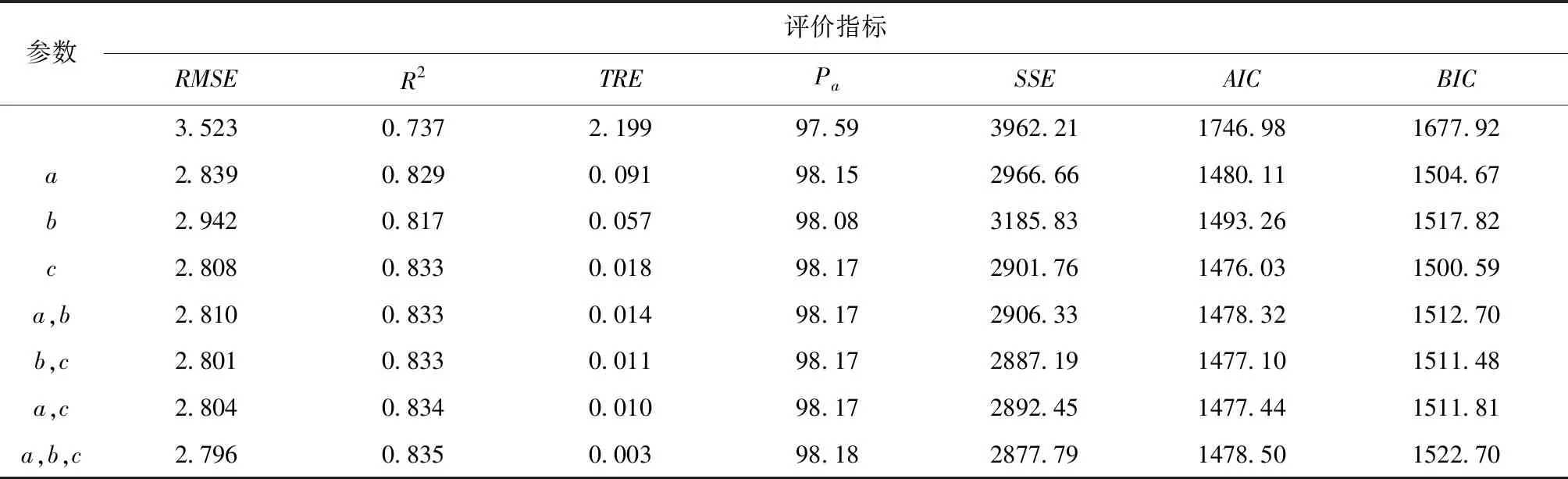
表9 竞争等级为哑变量的胸径生长模型评价指标Tab.9 Evaluation index of DBH growth model with dumb competition grade

D=(38.22×S01+40.94×S02+45.10×S03)×

Exp(-2.01×Exp((0.03×S01+0.022×S02+

0.013×S03)×A))

(14)

为反映立地条件对胸径生长的影响,在竞争等级哑变量模型基础上,将立地质量等级作为第二类哑变量引入模型中。各参数引入立地质量等级哑变量模型拟合效果评价指标结果如表10所示。

表10 立地质量等级和竞争等级为哑变量的胸径生长模型评价指标Tab.10 Goodness of fit and evaluation index of growth models of H

从表10可以看出,与竞争等级哑变量模型相比,引入立地质量等级哑变量模型的拟合优度和预估精度有所提高,模型R2,Pa值均上升,RMSE,SSE,AIC,BIC值均下降。比较不同参数模型评价指标结果,竞争等级哑变量在a,c参数,立地质量等级哑变量在c参数时,R2,Pa值最高,RMSE,SSE,AIC,BIC值相对较小,确定该参数模型作为胸径生长的哑变量模型,模型为:

D=(43.75×S1+34.69×S2+45.79×S3)×

Exp(-1.97×Exp(-(0.026×S11+0.019×

S12+0.016×S13+0.033×S21+0.026×

S22+0.019×S23+0.017×S31+0.018×

S32+0.011×S33)×A))

(15)

与胸径竞争等级哑变量模型相比,同时引入竞争等级和立地质量等级两个哑变量的胸径生长模型,决定系数R2为0.847,提高了1.56%；预估精度Pa值为98.25,提高了0.08%。

2.5 树高和胸径生长曲线

根据树高和胸径单个哑变量生长模型,分别拟合树高和胸径生长过程曲线,结果如图2所示。从图2中可以看出:1)树高的立地质量等级哑变量生长模型拟合曲线显示,各级立地质量等级下树高呈对数曲线生长,且Ⅰ级>Ⅱ级>Ⅲ级。中幼龄(林龄<60a)阶段均随年龄增长快速生长,差距较小；近熟林以后生长速度减缓,差距增加,但逐渐趋于稳定。说明树高后期生长在不同立地质量下表现出明显差异,生长趋于稳定后,可采用树高因子衡量立地质量等级。2)胸径的竞争等级哑变量生长模型拟合曲线显示,各级竞争等级下,胸径生长情况为Ⅰ级>Ⅱ级>Ⅲ级,随着年龄的增加,Ⅲ级竞争等级下的胸径生长速度明显低于Ⅰ级和Ⅱ级。中幼龄(林龄<60a)阶段,随年龄增长各竞争等级下胸径生长差距逐渐增大；进入成熟林阶段胸径生长速度减缓,各竞争等级间的差异基本趋于稳定。说明生长初期竞争对林木的径向生长影响较大,可通过不同的竞争程度,结合林分密度调控林木的干形；生长后期竞争对其径向生长影响不大,基本趋于稳定水平。

图2 不同立地和竞争等级下的树高和胸径生长模型曲线图Fig.2 Curve graph of H and DBH growth model at different site and competition level

根据最终确定的树高和胸径双哑变量生长模型,分别拟合树高和胸径生长过程曲线,结果如图3所示。从图3可以看出:

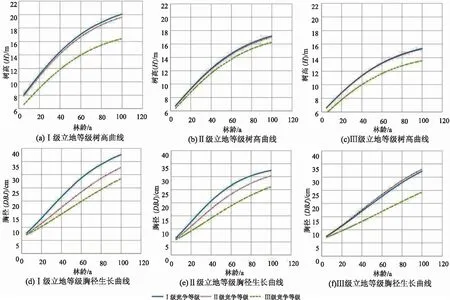
图3 不同立地等级和竞争等级下的树高和胸径生长曲线Fig.3 Curve graph of H and DBH growth model at different site and competition level

1) 树高双哑变量生长模型拟合曲线显示,在3种立地质量等级下,竞争等级Ⅰ级和Ⅱ级的树高生长过程均较为接近,Ⅲ级的树高生长明显偏低。说明在相同的立地条件下,Ⅰ、Ⅱ级竞争等级的栎类林树高生长差异不明显。本研究结果与曹梦等[20]研究的结果相似,即树高生长量受Ⅰ、Ⅱ级竞争压力时,表现的特征是一致的。比较不同立地条件下树高生长情况发现,在Ⅰ级立地质量等级下,不同竞争等级的树高生长差距最大,其次为Ⅲ级,Ⅱ级最小。

2) 胸径双哑变量生长模型拟合曲线显示:Ⅰ级、Ⅱ级立地质量等级下,不同竞争等级的胸径生长差异比较明显,但随着竞争程度的增加,胸径生长明显降低,且随着年龄的增长,生长差异逐渐增大；Ⅲ级立地质量等级下,林木竞争强度为Ⅰ级、Ⅱ级时,林木竞争对胸径生长的影响不明显。比较不同立地条件下胸径生长情况发现,胸径生长随着立地质量等级的降低、竞争的加剧而呈现整体降低趋势。

3 结论

1) 通过优势木的年均生长量与立地因子进行相关性和主成分分析,筛选出影响栎类林生长的主要立地因子,即海拔、坡向、土壤厚度,并按照分级赋分结果进行立地质量评价。结果显示,研究区域生长较好的栎类林主要分布于海拔1 000～2 000m 的阳坡或半阳坡,土层以中厚度适宜,这与栎类林在秦巴山区生长分布习性较为一致。

2) 树高生长基础模型以Gompertz最优,引入立地质量等级哑变量后,模型拟合优度和预估精度明显提升,以参数a,b上引入效果最优,决定系数R2为0.717,预估精度Pa为98.26,较基础模型分别提高16.59%和0.65%；进一步引入竞争等级哑变量后发现,竞争等级哑变量在参数a上时,模型综合评价效果最优,决定系数R2为0.745,预估精度Pa为98.35,较立地质量等级哑变量模型分别提高3.91%和0.09%。对于树高生长模型而言,在代表树木生长的最大值参数上引入立地类型哑变量的模型预估效果较好,当引入竞争类型哑变量时,依然是最大值参数上的预估效果较好。分析其原因,可能是树高最大值受立地条件影响更为显著,而树高生长速率主要是树种的遗传特性所决定。

3) 胸径生长基础模型以Gompertz最优,引入竞争等级哑变量后,以参数a,c上引入效果最优,决定系数R2为0.834,预估精度Pa值为98.17,较基础模型分别提高13.16%和0.59%；进一步引入立地质量等级哑变量后发现,立地质量等级哑变量在参数c上时,模型综合评价效果最优,决定系数R2为0.847,预估精度Pa值为98.25,较竞争等级哑变量模型分别提高1.56%和0.08%。对于胸径生长模型而言,在代表胸径最大值参数和生长速率参数上引入竞争哑变量有利于提高模型预估精度,而在生长率参数上引入立地等级哑变量有利于进一步提高模型预估精度。分析其原因,可能是胸径的生长速率与所处林分竞争和立地条件有密切关系,而对于胸径最大值更多还是受制于林分竞争等级的影响。

4) 不同立地条件下,栎类林树高生长情况为Ⅰ级>Ⅱ级>Ⅲ级,且近熟林以后生长差距明显增加,但其后,随着年龄增长基本趋于稳定。不同竞争等级下,栎类林胸径生长情况为Ⅰ级>Ⅱ级>Ⅲ级,随着年龄的增加,Ⅲ级的胸径生长速度明显低于Ⅰ级和Ⅱ级,成熟林阶段各竞争等级间的生长差异趋于稳定。树高生长过程在不同条件下表现为:立地质量等级为Ⅰ时,竞争等级Ⅲ与Ⅰ、Ⅱ的树高生长差距最大；而立地等级为Ⅱ、Ⅲ时,不同竞争等级间树高生长差异不明显。胸径生长过程在不同条件下表现为:立地质量等级为Ⅰ、Ⅱ时,不同竞争等级的胸径生长差异比较明显,其中以竞争等级Ⅰ的胸径生长最优；而在立地质量等级为Ⅲ时,竞争等级Ⅱ、Ⅲ对胸径生长的影响基本无差异。

综上所述,栎类林在不同立地条件、竞争压力下的胸径和树高的生长特点有所不同,但均以立地条件好(立地质量Ⅰ级)、竞争压力小(竞争等级Ⅰ级)的林分生长最优。由于立地质量短时间内无法改变或提升,因此,针对不同的立地条件应采取不同的经营措施,可促进栎类林健康稳定生长。立地质量等级为Ⅰ、 Ⅱ级的栎类林,可通过分析现有林分结构与相应立地条件下Ⅰ级竞争等级林分结构之间的差异,采取抚育采伐或人工更新等措施,调整林分结构,为林木生长创造良好的竞争环境,促进林木又好又快地生长。立地质量等级为Ⅲ的林分,特别是处于竞争等级Ⅰ、Ⅱ的中幼林,易采取自然修复为主的方式,通过封山育林、人工施肥、补植灌草等方式,改善林分条件,增加林木生长所需养分,促进天然更新。此外,本研究在建模过程中虽考虑立地因子、单木竞争因子,但由于林分水平的竞争难以量化,故评价效果有限。未来研究,可以通过研究林分空间结构,量化林分竞争,从而改善模型精度。