塔里木河流域胡杨生长模型研究

王庆杰,李国东,刘晓曼,安博文,计怀峰

(1.新疆财经大学 统计与数据科学学院,乌鲁木齐 830012；2.新疆农业大学 林学与园艺学院,乌鲁木齐 830052)

自1970年以来,气候变化和人为活动导致塔里木河流域范围内的水资源逐渐减少,其沿岸森林遭受水环境波动的影响,并导致沿岸森林发生缺口的频率增加[1]。在塔里木河两岸植被中,胡杨(Populuseuphratica)在维护两岸生态系统中起着重要的作用[2],开展胡杨的相关研究极其重要。

胡杨具有抗盐碱、抗旱等特性,是极端干旱沙漠地区唯一的乔木树种,对于维持荒漠地区生态平衡具有重要作用[3]。国内外很多学者对胡杨进行了多方面的研究:部分学者研究了其群落特征。如:朱雅丽等[4]采用相关及回归分析方法,将地上鲜生物量作为研究对象,通过胡杨冠幅构建不同函数形式的估测模型,并进行精度比较分析；高生峰等[5]通过对胡杨林的调查和测定,分析了水源距离对胡杨林群落特征的影响。部分学者研究了其光合作用、呼吸作用。如:周朝彬等[6]研究了不同保水剂处理下幼苗的叶片水势、光合和叶绿素荧光参数的变化,并探讨了胡杨对干旱胁迫的适应机制；李熙萌等[7]通过地下水埋深度差异,对胡杨叶片的呼吸作用特性进行了研究。部分学者研究了其扦插、育苗。如陈元宏等[8]为了给胡杨幼苗的培育和质量提升提供技术支持,对温室里胡杨的扦插育苗和管理方式进行了研究。部分学者在其异形叶方面有了新发现。如Li Cailin 等[9]为了探索circRNAs在胡杨假单胞菌(P.hl)的形态发生及其应激反应中的作用,通过链特异性RNA测序分析了4种异型叶片的circRNAs的表达谱。另外,还有一些学者对其精神进行了研究,陈玉萍[10]提出应该大力发扬“胡杨精神”,为新时代实现新疆高等教育现代化砥砺前行,坚持不懈。

树木在生态系统平衡中发挥着非常大的作用,因为其本身不仅具备生态研究价值、还具备经济研究价值,所以研究树木生长模型在生态平衡中极为重要。许业洲等[11]分析了罗田垂枝杉的生长过程和生物量变化规律；孟得干等[12]在对3种天然林分生长模型进行拟合和检验的同时,也对3种林分类型的生长规律进行了研究；曾伟生等[13]建立人工杨树生物量模型,分析生产力与气候因子间的关系；韩金等[14]基于几种常见的理论生长方程,对将乐国有林场不同立地条件下杉木人工林胸径的生长过程进行了拟合；薛春泉等[15]将异速生长方程与理论生长方程相结合,预测了广东省木荷生物量动态。

在树木生长模型方面,学者虽已做出了相关的研究,但是针对胡杨生长模型方面的研究比较少。由于胡杨的稀少导致其各方面的数据一般难以获取,所以利用现有数据开展胡杨生长模型的研究尤其重要。本文针对胡杨的生长模型进行分析与研究,旨在通过评价与比较得出最优的生长模型,为沙漠地区调查胡杨的生长情况提供参考。

1 材料与方法

1.1 研究区概况

1.2 数据来源

2017年9月,通过在塔里木河流域阿拉尔地区的阿拉尔市、十二团及周边地区,根据不同土壤类型(湿地、较湿地、沙地)选择了不同的样地,挑选无生长缺陷、树干生长正常的胡杨作为备选样本。收集到关于胡杨胸径、材积、树高、树龄以及含水量等方面的数据共78组。本文为得到更加适宜当地沙漠气候生存的胡杨生长模型,将78组数据分为建模数据41组、检验数据37组。通过41组数据进行生长模型建模以及37组数据进行生长模型检验,进一步研究生长模型之间通过对比是否可以得到最优的模型。

将胸径、树高、材积分别与树龄构建模型,通过运用SPSS 22.0,Excel 2010和Origin 9.0,并结合设定的模型评价标准得到适合塔里木河流域的胡杨生长模型。胡杨树木的基本统计量信息(树龄、树高、胸径、材积的最大值、最小值、均值、标准差)如表1所示。

表1 建模数据和检验数据的基本情况统计Tab.1 Basic statistics of modeling data and testing data

1.3 研究方法

1.3.1模型选择

目前,在树木生长模型的选择上,已经存在许多相关的模型,所以在生长模型方面,理论及应用已经有据可依。本文选择普遍选用的经验方程及理论方程(表2)。经验方程有柯列尔、豪斯费尔德、修正威布尔、吉田正男、斯洛波达、幂函数、对数、双曲线、混合型等；理论方程有单分子式、坎派兹、考尔夫、舒马切尔、逻辑斯蒂、理查德、莱瓦科威尔[18]。通过将建模数据带入上述方程中分别进行建模,依据所设定的检验以及评价标准进行对比,以期得到最优的生长模型。

表2 经验方程和理论方程Tab.2 Empirical model and theoretical model

1.3.2模型的检验

为了对模型进行比较,选取平均绝对误差(MAE)、决定系数(R2)、均方根误差(RMSE)来对模型进行评价。

平均绝对误差(MAE):

(1)

均方根误差(RMSE):

通过结构分析可知，飞行中该拉杆主要承受轴向拉压载荷，要测得拉杆拉压载荷，需要在拉杆上粘贴垂直组合应变计。常规等截面细长拉杆一般在拉杆中间对称粘贴应变计，对侧组桥即可。该机拉杆属于非常规细长拉杆，结构如图2。拉杆结构左右对称，由螺纹杆、耳环套筒(内含螺纹)、连接螺栓等组成，其中螺纹杆直径6 mm，套筒直径14 mm，图中标出了套筒内部螺纹区域。

(2)

决定系数(R2):

(3)

1.3.3模型的评价

将检验数据分别带入所建立的树高与树龄、胸径与树龄、材积与树龄的各模型中,分别计算出各模型的平均误差(ME)、平均预测误差百分比(MPSE),用以衡量所建立的生长模型是否符合精度标准[19]。

平均误差(ME):

(4)

平均预测误差百分比(MPSE):

(5)

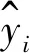
2 结果与分析

2.1 树高、胸径、材积拟合结果

胡杨树高、胸径、材积生长模型的研究,可以在一定程度上为其生长趋势和造林设计等方面提供参考依据。首先将胡杨的树龄设为自变量t、树高设为因变量y1、胸径设为因变量y2、材积设为因变量y3,将其分别带入经验方程与理论方程中进行建模。将这些指标的数据分别带入上述16种方程中,可以得出每个模型的拟合结果。拟合结果如表3、表4、表5所示。

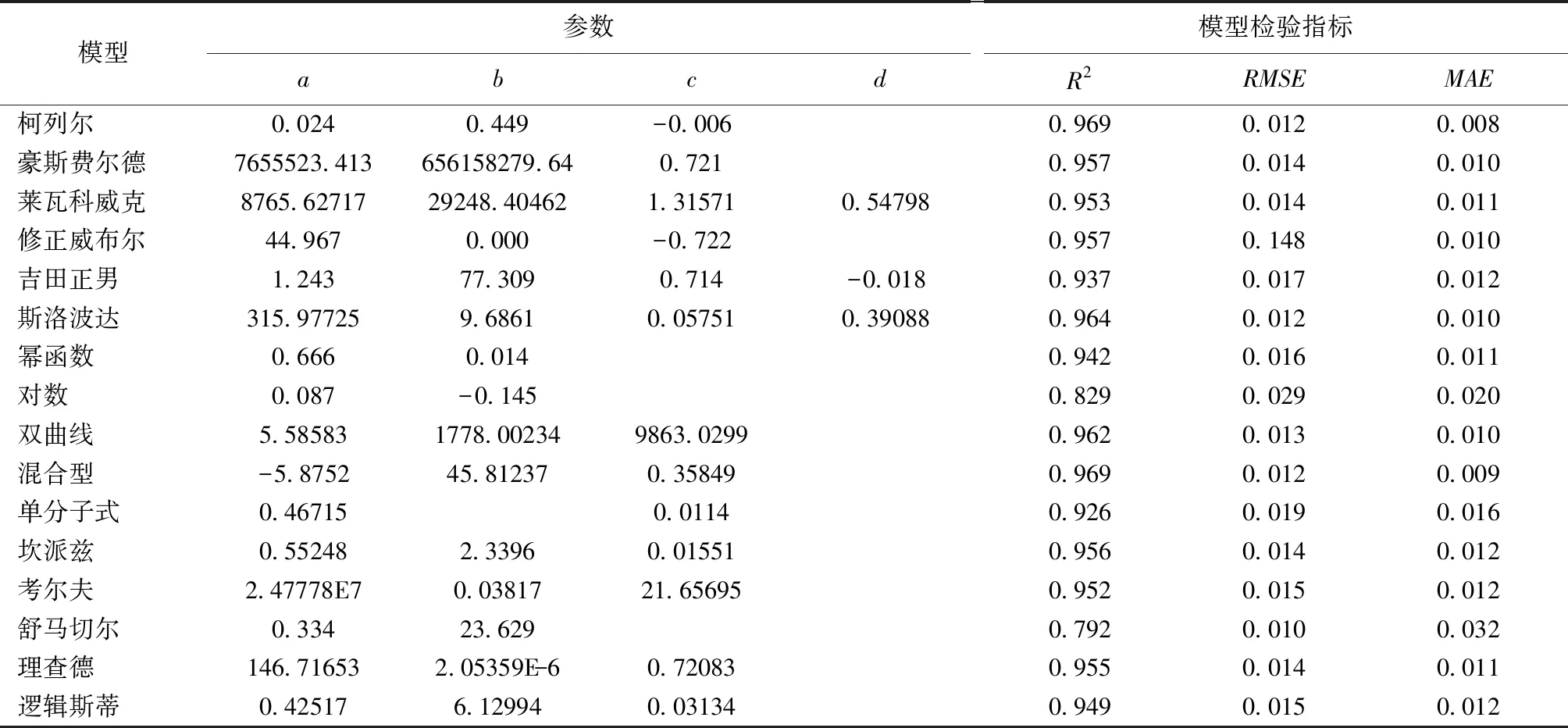
表4 胸径各方程拟合结果Tab.4 Fitting results of equations for breast diameter

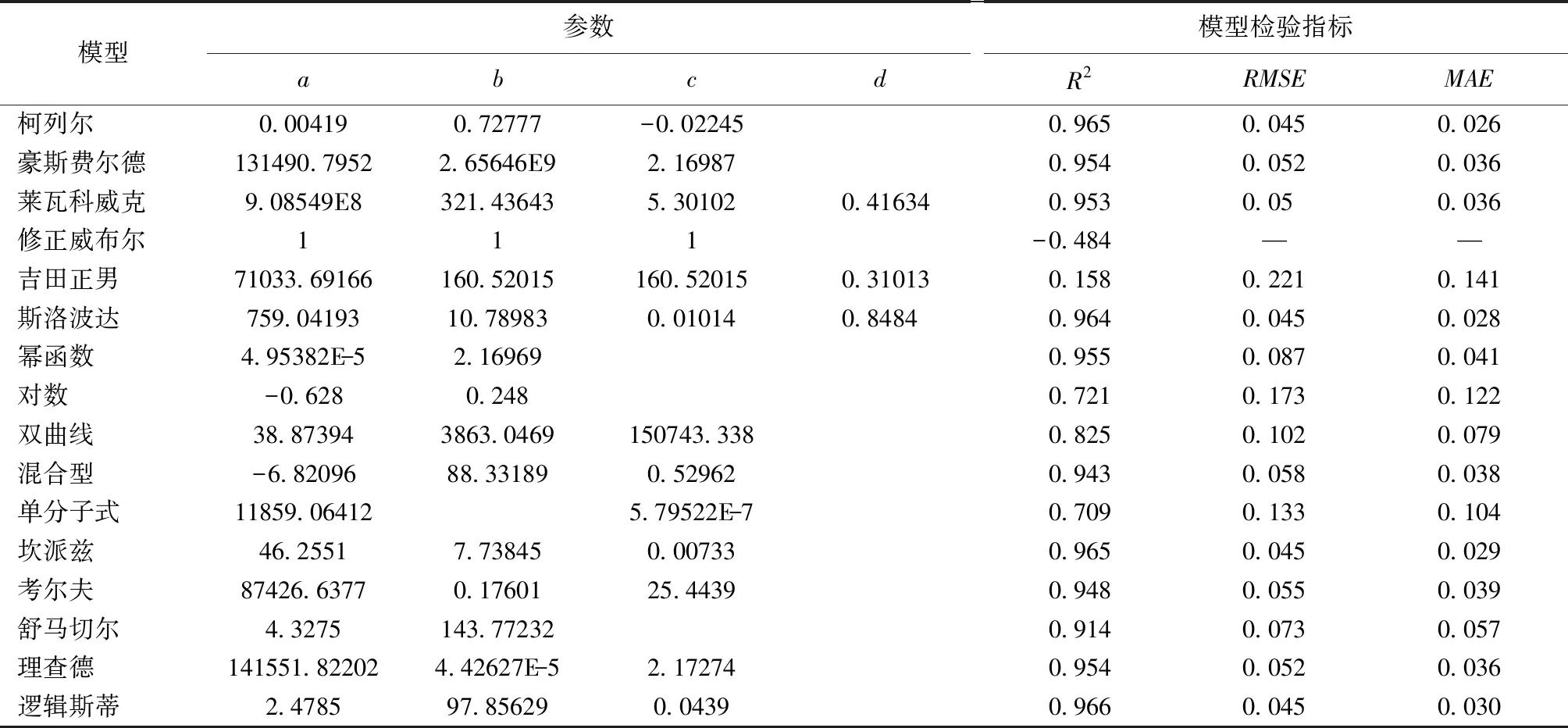
表5 材积各方程拟合结果Tab.5 Volume equation fitting results

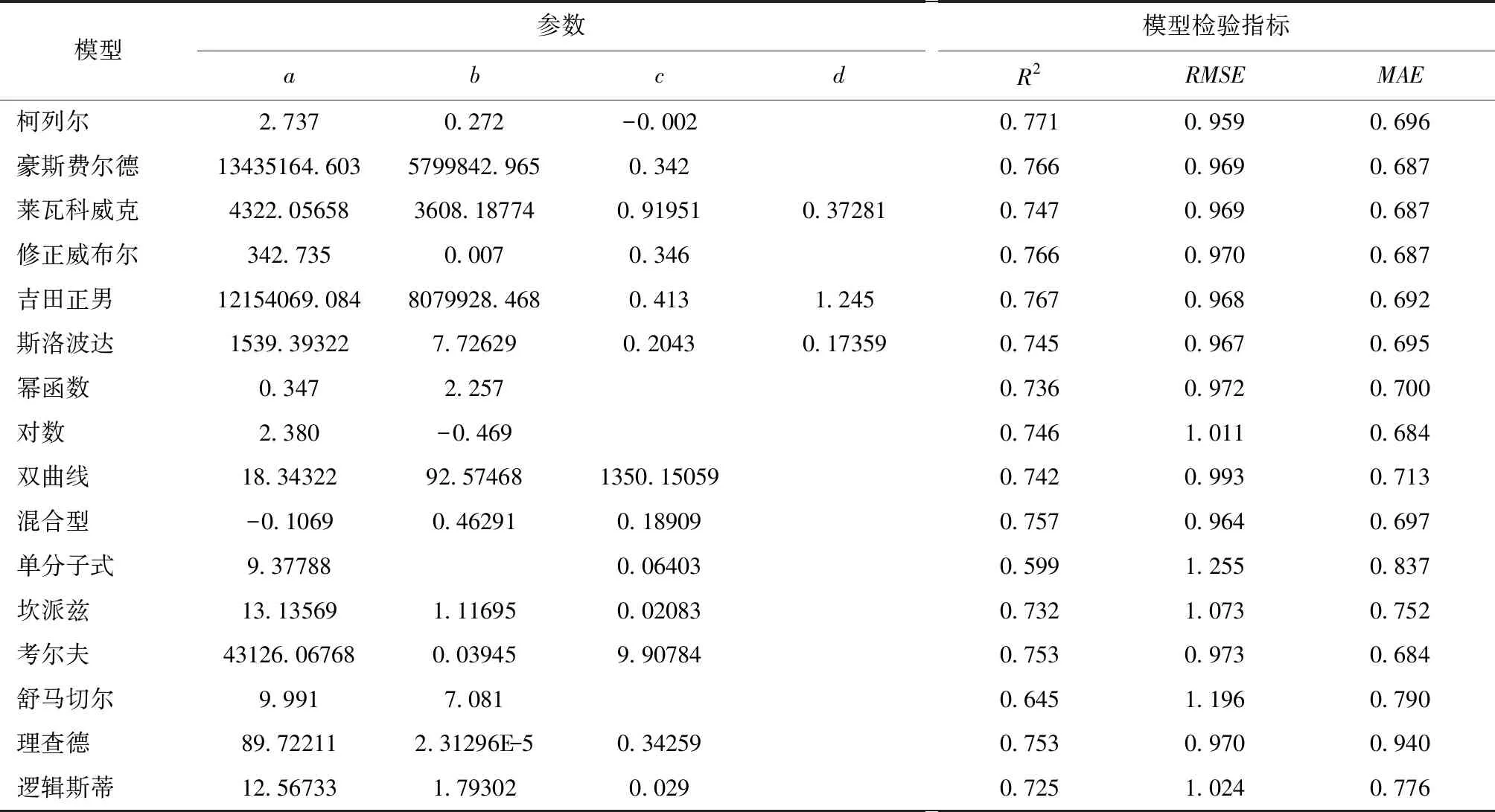
表3 树高各方程拟合结果Tab.3 Fitting results of tree height

2.2 树高、胸径、材积拟合结果分析

通过将建模数据带入上述16种方程可得到树高、胸径、材积的经验模型与理论模型的拟合结果,再进一步计算可得出各模型的MAE,RMSE的值。模型拟合的优劣可根据R2的值大小来进行比较,即:当R2的值越接近于1,可说明该方程的拟合度越高；反之,拟合度越小。拟合度越高,表明模型越能准确预测变量的变化趋势。同时,MAE,RMSE的值越小,更可进一步说明前面所选模型的误差越小。可依据以上规则选出最优模型。

依据树高的拟合结果,各个模型的R2值大部分达到0.6以上,唯有单分子式的R2值为0.599。依照R2的值大小可以对各个模型进行排序,得出其排序结果为(1)>(4)>(2)=(3)>(10)>(14)=(8)>(15)>(7)>(5)>(9)>(6)>(13)>(16)>(11)>(12)。对比MAE,RMSE的值可发现:各个模型的RMSE值都在1.26以下,柯列尔的RMSE值最小、单分子式的RMSE值最大；除理查德模型外,其余模型的MAE值都在0.84以下,对数以及考尔夫的MAE值最小,理查德的MAE值最大。由于R2值反映的是模型的拟合度,所以在选择模型时,以R2值为第一参考标准。鉴于柯列尔模型的R2值最大、RMSE值最小,MAE值在一定程度上具有代表性,因此选择柯列尔作为树高生长模型((6)式)。

y1=2.737t0.272e0.002t

(6)

依据胸径的拟合结果,各个模型的R2值大部分达到0.8以上,唯有舒马切尔的R2值为0.792。依照R2值的大小可以对各个模型进行排序,得出其排序结果为(1)>(10)>(5)>(9)>(2)=(3)>(13)>(8)>(15)>(14)>(16)>(6)>(4)>(12)>(7)>(11)。对比MAE,RMSE的值可发现:各个模型的RMSE值都在0.15以下,舒马切尔的RMSE值最小、修正威布尔的RMSE值最大；各个模型的MAE值都在0.032以下,柯列尔的MAE值最小,舒马切尔的MAE值最大。由于R2值反映的是模型的拟合度,所以在选择模型时,以R2值为第一参考标准。鉴于柯列尔、混合型的R2值相同、RMSE值相同、MAE值存在0.001的差距,暂时将两个方程都选取作为胸径生长模型,通过后面的检验数据进一步选择更优的模型。柯列尔、混合型表达式如(7)式、(8)式所示:

y=0.024x0.449e0.006x

(7)

(8)

依据材积的拟合结果,各个模型的R2值大部分达到0.7以上,唯有修正威布尔、吉田正男的R2值异常。依照R2的值大小对各个模型进行排序,得出排序结果为(16)>(1)=(13)>(5)>(6)>(2)=(8)>(15)>(14)>(10)>(11)>(9)>(7)>(12)>(4)>(3)。对比MAE,RMSE的值可发现:各个模型的RMSE值都在0.221以下,斯洛波达、柯列尔、坎派兹的RMSE值最小,吉田正男的RMSE值最大,修正威布尔的RMSE值不存在；各个模型的MAE值都在0.141以下,柯列尔的MAE值最小,吉田正男的MAE值最大。由于R2值反映的是模型的拟合度,所以在选择模型时,以R2值为第一参考标准。鉴于逻辑斯蒂模型的R2值最大、RMSE值最小、MAE值在一定程度上具有代表性,因此选择逻辑斯蒂作为材积的生长模型((9)式)。

(9)

2.3 模型的适应性检验

通过上述表3—表5拟合对比结果的分析可知:树高的生长模型可以选取柯列尔模型、材积的生长模型可选取逻辑斯蒂模型,由初步的建模数据可得知胸径的柯列尔、混合型拟合度相同。此时,通过将检验数据分别带入所选取的各预测模型,计算得出相应的预测值及ME,MPSE值(表6)。

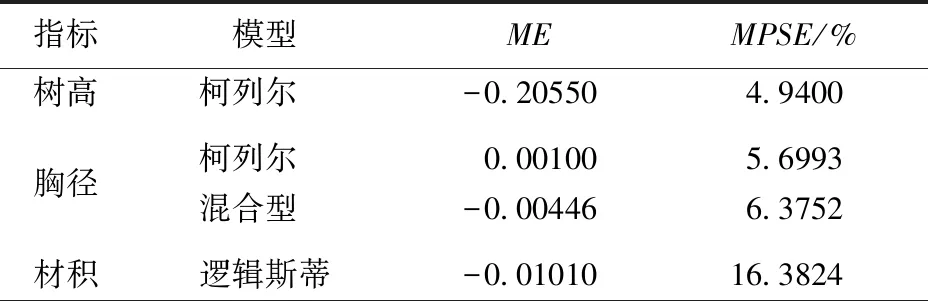
表6 树高、胸径、材积检验结果Tab.6 Test results of tree height,breast diameter and volume

从表6可知,所选模型的ME绝对值都在0.21以下,MPSE的值均在16.39%以下。胸径生长模型的选取:通过将两个模型的ME,MPSE值进行对比,可得知柯列尔的ME,MPSE值均最小,本文最终选择柯列尔作为胸径的生长模型。通过对ME值进行对比可得知,胸径的预测模型效果最好,树高的预测模型效果较差；通过对MPSE的值对比可得知,树高的预测模型效果最好,材积的预测模型效果较差。

根据上述规则所选取的树高、胸径和材积的生长模型,把作为检验数据的自变量带入,可得出各自的预测值。通过将各自的标准化残差视为纵坐标,各个模型的预测值视为横坐标,可以绘制出各个模型的残差图,即树高残差图(图1)、胸径残差图(图2)、材积残差图(图3)。由残差图可看出残差值呈现出了随机波动的趋势,标准化残差值均在±2范围内波动。这表明,所选拟合树高、胸径、材积生长的模型满足随机误差正态分布,回归效果较优,可尝试运用所选模型进行相关数据预测。将上述所得到的各自预测值以及真实值视为纵坐标,树龄视为横坐标,可以绘制出树高生长曲线(图4)、胸径生长曲线(图5)、材积生长曲线(图6)。

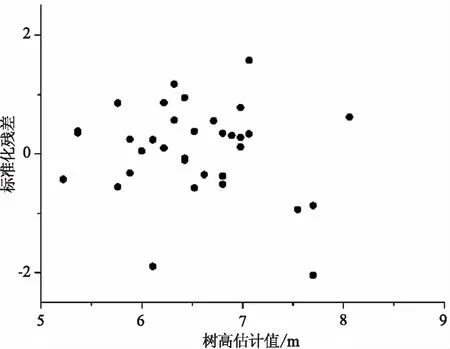
图1 树高残差图Fig.1 Tree height residual plot

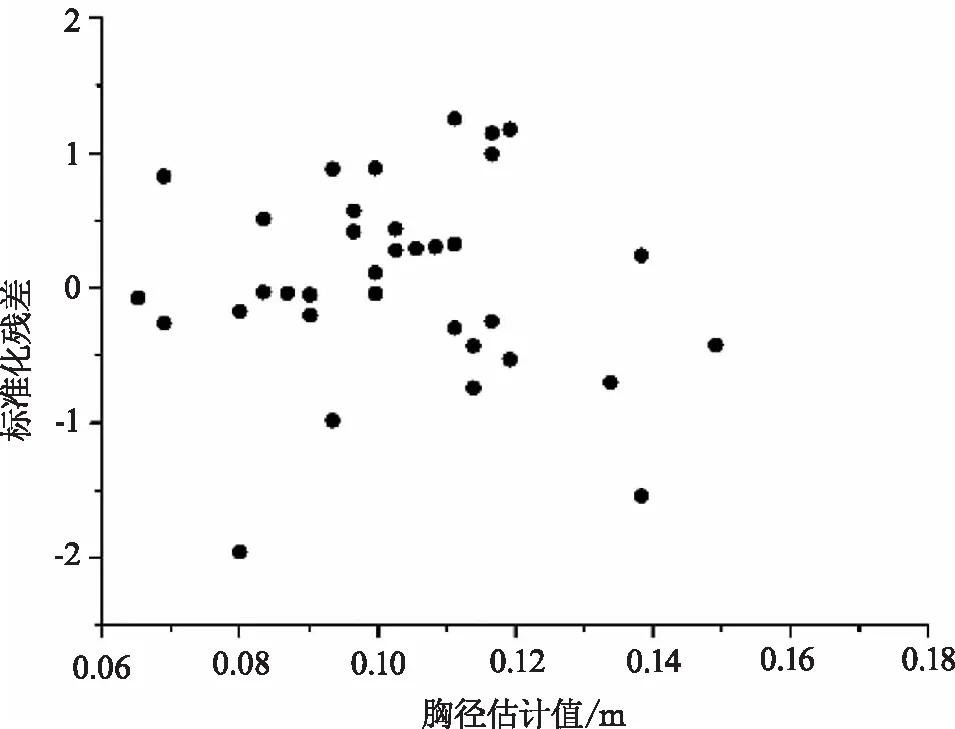
图2 胸径残差图Fig.2 Diameter residual plot at breast height

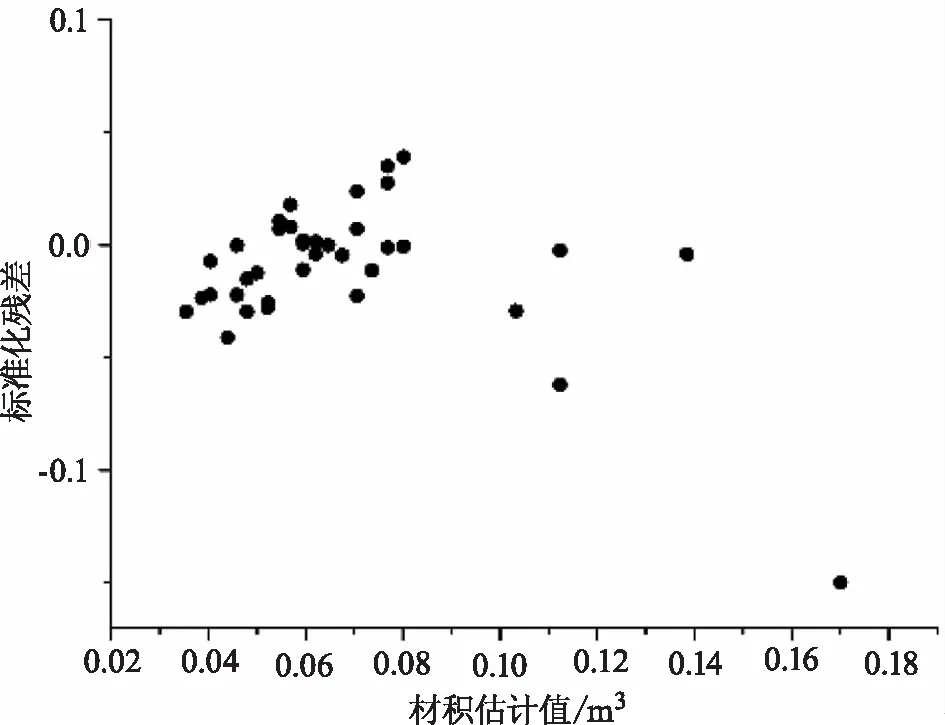
图3 材积残差图Fig.3 Volume residual plot

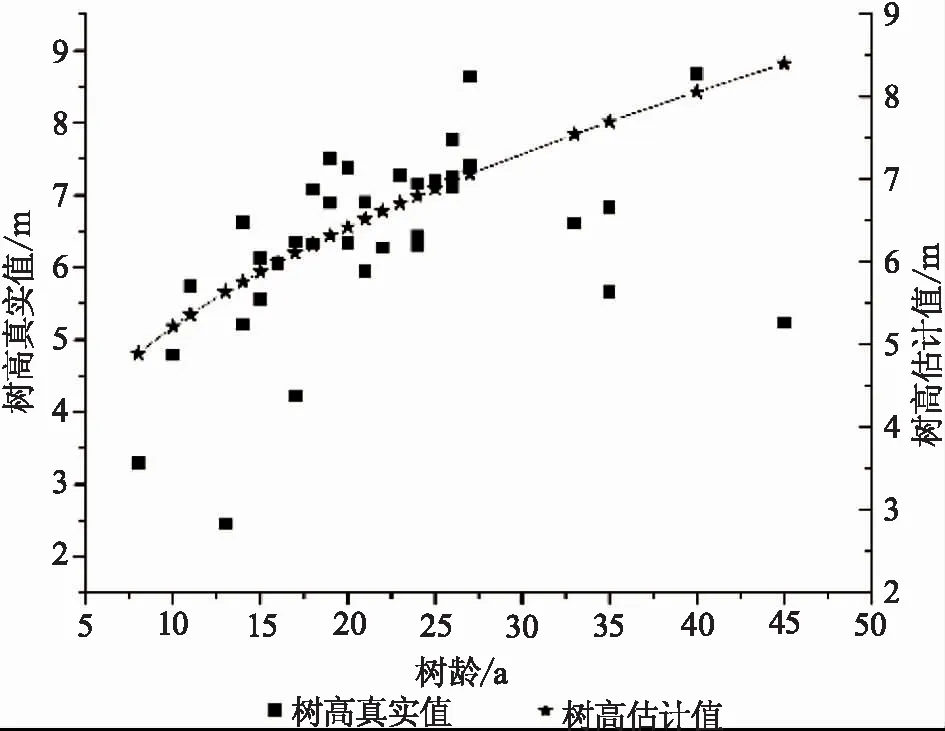
图4 树高生长曲线Fig.4 Tree height growth curve

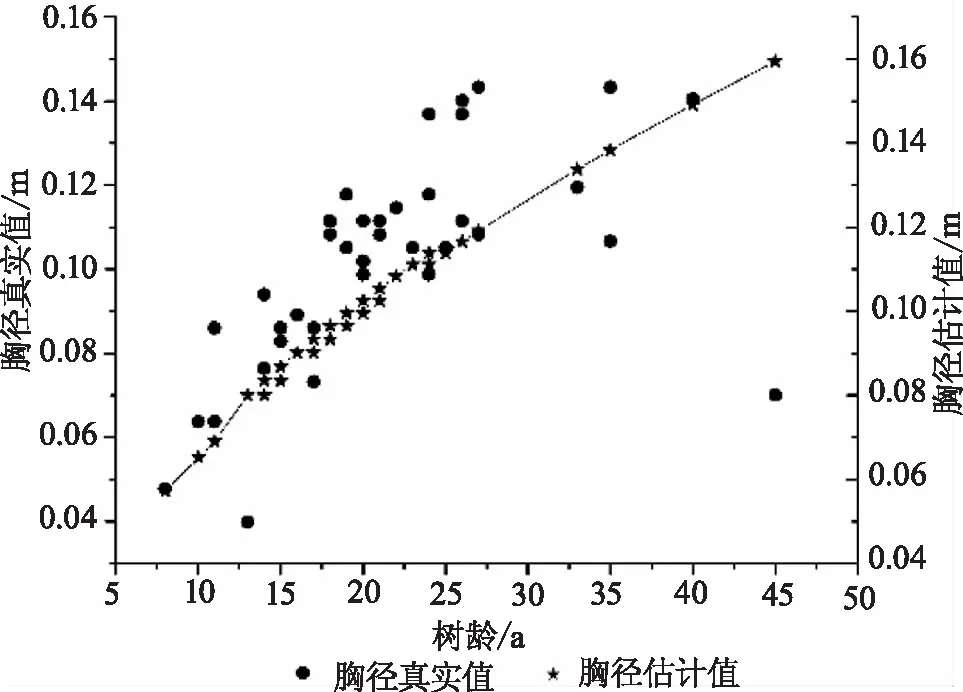
图5 胸径生长曲线Fig.5 Diameter growth curve at breast height

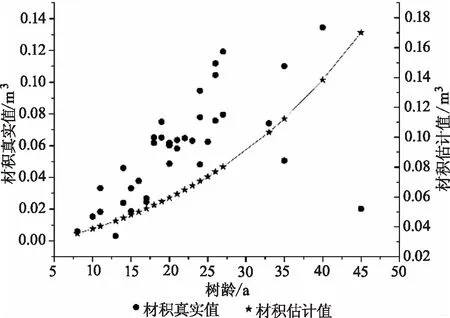
图6 材积生长曲线Fig.6 Volume growth curve

3 结论与讨论

通过利用建模数据,以柯列尔、舒马切尔、单分子式等方程视为胡杨树高、胸径、材积生长模型拟合的切入点,结合相关文献的模型评价方法,得到了胡杨相关因素的生长模型。通过结合前期设定的检验标准,初步选取了决定系数为0.771、平均绝对残差为0.696、均方根误差为0.959的柯列尔方程视为树高的生长模型；决定系数为0.966、平均绝对残差为0.030、均方根误差为0.045的逻辑斯蒂方程视为材积的生长模型。后期通过带入检验数据结合平均误差、平均预测误差百分比,得到了选取的树高、胸径生长模型评价值,得到了平均误差、平均预测误差百分比分别为0.001 0m,5.699 3%的柯列尔方程作为胸径的生长模型,并且树高、材积的相应指标值在一定程度上也具有代表性[20]。

曾有研究者以南疆胡杨茎为研究对象,利用计算机技术以可视化的形式描述该植物的生长状态[21]。由于单一模型的拟合效果可能达不到较优的效果,通过对树木的多种生长模型进行拟合,并进行对比可得到拟合效果较优的生长模型。本研究为胡杨这一珍稀树种的生长可视化提供了参考依据,也为当地其他树种的研究提供了参考方案,还为当地造林规划设计等方面提供了参考资料。但是对胡杨相关因素所进行的研究,是从理论的角度进行的,没有加入当地气候条件、降雨量、人类活动等因素来进行深入研究。如果考虑加入这些因素进行研究,进一步调研更多的样本,或许可得到预测精度更高的生长模型。