基于MATLAB的6R机器人轨迹规划速度分析

杨广新

（1.浙江信息工程学校，浙江湖州 313000；2.湖州工程技师学院，浙江湖州 313000）

0 引言

随着产业升级，迫切需要对机器人的设计进行深入的研究[1]，因此分析和掌握机器人轨迹规划特性至关重要。

目前机器人关节空间轨迹规划方法比较多，但多集中在采用多项式实现关节空间的轨迹规划。孙增光等[2]研究了三次多项式和五次多项式实现IRB2400 机器人的关节空间轨迹规划算法，并对规划效果进行对比。李林升[3]采用组合的5-5-7-5 次复合多项式实现PUMA560 机器人关节空间轨迹规划，计算量较大，需要采用高性能计算机实现关节空间轨迹规划。刘贝贝等[4]在5 次多项式基础上融合了均匀5 次B 样条曲线进行机器人关节空间轨迹规划，实现较好的控制效果。此外，梅江平等[5]提出5 次非均匀有理B样条实现Delta机器人关节空间轨迹规划。

机器人速度雅可比矩阵（简称雅可比）表示在具体位置关节处操作空间速度与关节空间速度之间的线性映射关系。机器人速度雅克比矩阵是机器人操作空间速度分析的关键要素，机器人在不同位置，雅克比矩阵的值是不同的。机器人速度雅克比矩阵求解比较困难，许多学者针对机器人的构型不同研究出不同的机器人速度雅克比矩阵求解方法，但目前主要采用微分变换法、直接构造法和矢量叉乘法等[6-7]。

本文以6R 机器人为研究对象，根据D-H 参数法建立6R机器人运动学方程；在此基础上，根据直接构造法构建6R机器人速度雅克比矩阵，对机器人关节空间和操作空间速度关系进行仿真分析，研究机器人三次多项式轨迹规划对操作空间速度连续性及变化的影响。

1 机器人运动学分析

1.1 D-H建模

D-H机器人建模方法由Denavit和Hartenberg提出。如图1所示，两个构件相连，中间关节轴线有两条公法线与其垂直，每条公法线对应一个连杆，如Zn分别与公法线an和an+1垂直。两公法线之间的夹角为转动角，记为θn，其转向按绕轴线Zn的右手螺旋法确定。

图1 D-H连杆模型

在每个构件上固结一坐标系，固结在杆n 上的坐标系为onxnynzn，其中坐标系原点on为关节轴线zn与an的交点，xn与公法线重合，zn与关节轴线重合。坐标系onxnynzn可以通过坐标系on-1xn-1yn-1zn-1绕xn-1轴转角an，沿xn-1轴平移an，绕zn轴转角θn，然后沿zn轴平移dn四步获得，则变换矩阵如下：

式中：cn为 cos θn；sn为 sin θn； sαn为 sinαn； cαn为 cosαn。

式中： nx、ny、nz，ox、oy、oz，ax、ay、az分别为末端执行器的单位主矢量x、y、z 相对于i关节坐标系的x、y、z 的方向余弦； px、py、pz为末端执行器的坐标原点相对于i关节坐标系的 x、y、z 的位置。

当i=0时，表示在机器人的基坐标系与工具坐标系之间的变换。

1.2 机器人运动学

机器人关节连杆参数如表1所示。

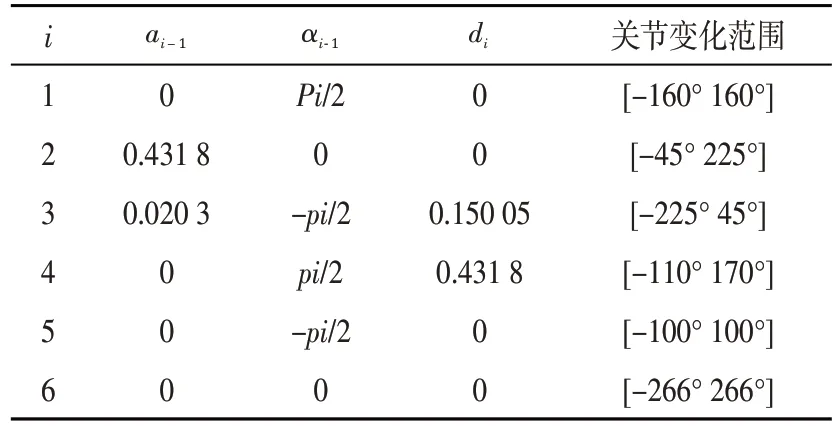
表1 6R机器人连杆参数

根据D-H方法，第i个关节坐标系到第i+1个关节坐标系的变化如下：

2 机器人速度雅克比矩阵的构建

2.1 机器人速度雅克比矩阵

6R机器人关节变量采用向量θ表示如下：

因此，关节空间的微小运动可表示为：

机器人工具坐标系在操作空间的位姿为X，其是关节变量的函数，如下所示：

式中： X 为6 维列矢量； J(θ) 为6R 机器人的速度雅可比（Jacobian）矩阵，其由函数x、y 的偏微分组成，反映了关节空间微小运动dθ与工具坐标系之间微小运动dX 之间的关系，同时也反映了机器人末端工具坐标系在操作空间的位姿变化速度与机器人关节变化速度之间的线性关系，该线性变换与机器人的位置相关。

对于6R机器人，根据机器人运动学方程，可以获得直角坐标位置向量[x, y, z]T的显式方程，但找不到方位向量[ωx，ωy，ωz]T的一般表达式。采用雅克比矩阵构造法可以更方便求出机器人雅克比矩阵。

对于转动关节，关节n 只绕zn轴以角速度θ˙n转动，机器人末端在操作空间位姿速度按如下构造：

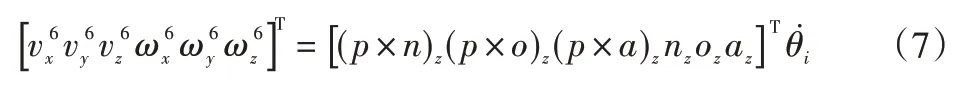
6R机器人6个关节均为旋转关节，6R机器人雅克比矩阵根据式（7）进行构造，如下所示：

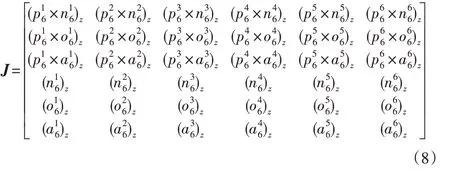
2.2 机器人速度雅克比矩阵构造

机器人速度雅克比矩阵构造步骤如下：

（1）计算各连杆变化矩阵如式（3）；

（3）按式（8）构造J的各列元素。

3 仿真分析

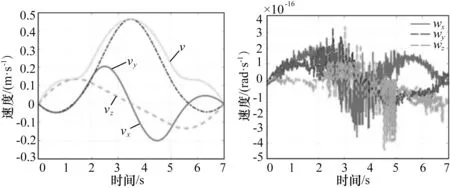
6R 机器人依次经过点P0、P1、P2和P3，对应时间序列为0 s，2 s，5 s和7 s。操作空间点P0～P4对应的关节值如表2所示。经过MATLAB 三次多项式关节空间轨迹规划，各关节位置曲线和速度曲线如图2 所示。由图可知，6R 机器人关节空间位置和速度连续，机器人运行平稳。根据三次多项式关节空间轨迹规划结果，对机器人相对于基坐标系的操作空间速度进行分析，如图3 所示。机器人操作空间沿基坐标系X、Y和Z 方向及合成速度均连续；沿基坐标系X、Y 和Z 轴的旋转角速度不连续，但数值为1×10-16级别，此不连续是由MATLAB计算误差造成的。

表2 关节位置序列 rad

图2 关节位置速度曲线图

4 结束语

采用速度雅克比矩阵直接构造法原理，给出6R机器人速度雅克比矩阵构造过程，机器人力雅克比矩阵是速度雅克比矩阵的转置，对于6R机器人受力研究具有重要意义；在机器人三次多项式关节空间轨迹规划中，机器人关节空间及操作空间运行速度均连续，机器人运动平稳，适合机器人PTP 轨迹规划要求。