基于改进极限学习机和深度神经网络融合的车辆轨迹长期预测＊

谭紫阳 高忠文 邓宇

（1.哈尔滨理工大学，哈尔滨 150080；2.西安交通大学，动力工程多相流国家重点实验室，西安 710049）

1 前言

轨迹预测是智能汽车进行可行域判断的基础[1]。目前，车辆轨迹预测主要采用基于物理的运动模型（Kinematic Model）和基于机器学习的模型。其中，基于物理的运动模型，如运动学和动力学模型，将车辆视为受物理定律支配的对象，主要控制输入和车辆状态[2]。这种预测方法对于短期轨迹预测是相当准确的，但对于长期轨迹预测（超过1 s）不可靠。这是因为没有考虑驾驶员操纵车辆引起的运动变化，而且机动目标运动轨迹非常复杂，要得到准确目标位置的表达式非常困难，且建立的模型很难与目标的真实运动特性相吻合，预测模型及其方法难以选择，而且会导致预测位置偏差大，预测精度不够高。为了解决这个问题，谢彬等提出了一种基于轨迹相似度的轨迹预测算法，在轨迹模式匹配过程中，查询当前轨迹与历史轨迹模型的相似度[3]。范文超等针对高斯混合模型的运动目标检测算法的不足，提出一种基于分块思想和高斯模型数量自适应的高斯混合算法[4]。

基于机器学习的轨迹预测主要对马尔科夫模型、概率图模型[5]、支持向量机模型[6]、神经网络模型等机器学习模型进行改进，挖掘移动对象历史轨迹的行为特征，实现移动对象轨迹预测。特别地，长期短期记忆（Long Short-Term Memory，LSTM）网络已成功应用于分析数据中的时间结构[7]以及横向位置预测[8]和驾驶员意图预测[9]等领域。Byeoungdo Kim 直接将LSTM 网络应用于预测车辆在网格上的轨迹[10]。Florent Altché 提出了一种用于公路轨迹预测的LSTM网络，该网络利用了目标车辆周围车辆的信息[11]。分析现有的机器学习模型可以发现：高斯和马尔科夫等模型的训练需要耗费大量时间[12-14]，预测的时空复杂度高，不能满足实时预测的要求；时间序列法易受外界条件影响，预测精度较低。此外，因为前期模型的训练不足，对于不同类型的道路会无法适应。

针对上述问题，为了更加可靠地预测车辆轨迹，本文提出一种基于深度神经网络（Deep Neural Networks，DNN）的多元信息融合方法来解决回归问题，以期在1 s、2 s、3 s 的预测中得到较好的效果。

2 融合的神经网络模型

2.1 模型结构

为了更加可靠地预测车辆轨迹，本文提出了一种基于深度神经网络的多元信息融合方法，利用DNN、极限学习机（Extreme Learning Machine，ELM）建立模型，该模型将车辆速度、加速度、偏航角速度、转向角和道路曲率作为输入。深度神经网络可以通过输入数据、模型建立训练和测试网络进行预测[15-16]。极限学习机的优势有[17]：需要手动设置的参数只有隐含层结点个数，算法执行过程中不需要人工调整参数；避免了传统训练算法反复迭代的过程，快速收敛，极大地缩短了训练时间；所得解是唯一最优解，保证了网络的泛化性能。将相同数据分别输入到2 个性能不同的神经网络（DNN、ELM），将2个神经网络融合，可获得不同神经网络的优点。因此，多信息融合系统将比使用单个网络具有更好的性能。其中，融合系统分为3个部分：数据处理、信息收集和结果信息融合。采用基于深度神经网络的信息融合预测方法可以构建无需设计且具有复杂方程的系统模型。此外，通过扩展当前的仿真场景，该方法可以很容易地扩展到在各种驾驶场景中预测车辆的轨迹。

将输入数据归一化到[-1,1]范围内，主要方法是将信息反映到共同的描述空间，然后单独输入2个神经网络，其中DNN 和ELM 的隐藏层分别为hDNN、hELM，然后通过1个完全连接（融合）层融合2个神经网络的隐含层输出，模型结构如图1所示。将来自融合层的输出传递到输出层进行预测，输出层分别计算1 s、2 s、3 s预测的横向和纵向位置。融合层执行的计算为：

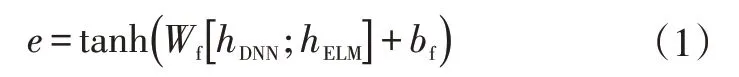
式中，Wf、bf为学习到的模型参数；e为融合层的输出。

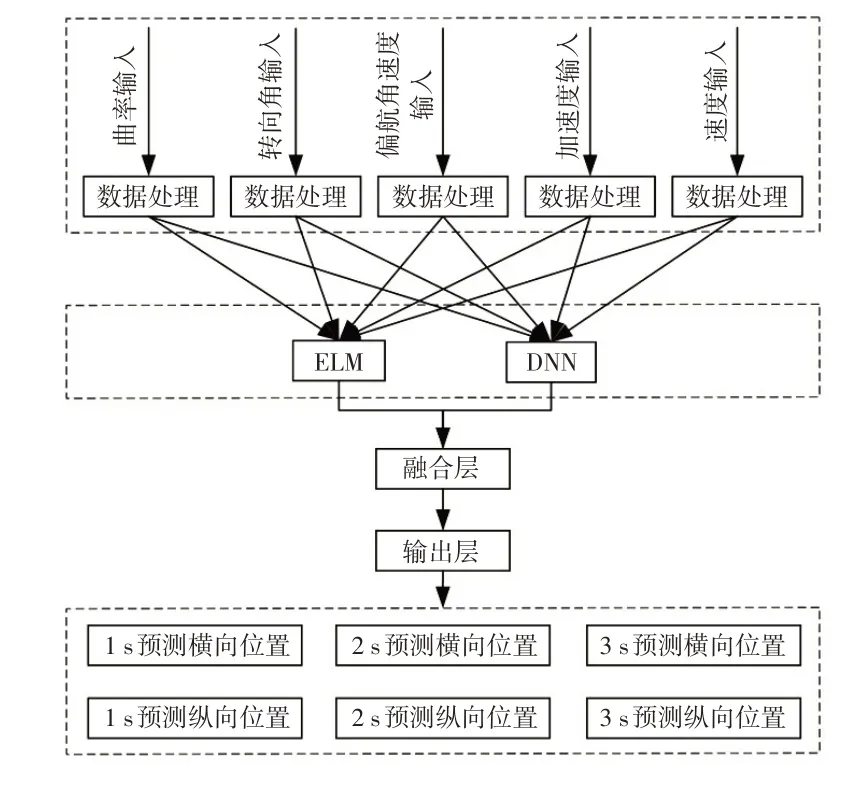
图1 模型结构

训练过程的损失函数采用预测轨迹与地面真实轨迹之间的均方误差（Mean Square Error，MSE）：

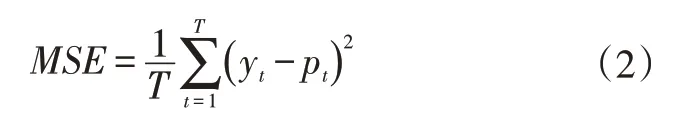
式中，yt为t时刻的实际位置；pt为t时刻位置的预测值；T为总体时间。

此时，神经网络结果的融合已经生成，信息融合已经完成。

2.2 DNN网络设计

DNN 用于轨迹预测时，可以对各种驾驶条件和驾驶模式进行训练，在离线阶段的训练过程中计算连接的权重。为了提高车辆轨迹预测的准确性，进行了离线训练，其中包括各种道路曲率的各种驾驶场景。输入的数据经过输入层和多个隐藏层到达输出层，每个层由几个节点组成。数据在层间传输时需要乘以权重，隐藏层需要通过激活函数将数据传送到下一层。Sigmoid和双曲正切函数是常用的激活函数，但是，这两种激活函数可能产生梯度消失的问题，因为当存在许多隐藏层时，数据不会正确地传播到输入层，这影响了网络的成功训练。此问题可以通过使用修正线性单元（Rectified Linear Unit，ReLU）函数替换激活函数来解决，ReLU 函数在输入数据大于零时输出与输入相同。然而，ReLU函数不适合在本模型中使用，因为DNN 模型的最终输出包括预测未来的横向运动。这里使用带泄露修正线性单元（Leaky ReLU）激活函数，Leaky ReLU 激活函数与原始ReLU激活函数的定义有所不同，其定义为：

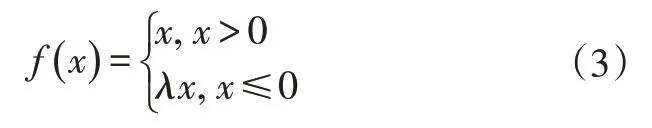
式中，λ=0.15为固定常数。

成本函数将输入所需的值和输出值作为输入来计算成本C：

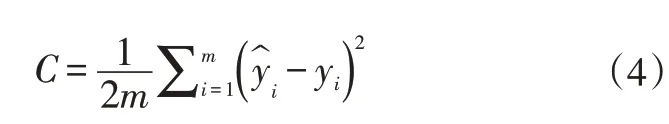
式中，m为用于培训的数据集的数量；为DNN的输出值；yi为期望值。

为实现成本最小化，使用梯度下降算法来更新权重：

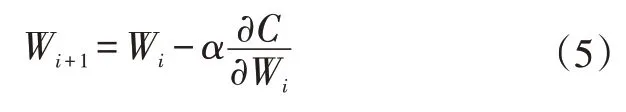
式中，α为学习率；Wi为i时刻的权重。

然后使用均方根反向传播（Root Mean Square Propagation，RMSProp）算法来优化深度神经网络，该算法使用变量M(w,to)来保留前一时间段每个周期梯度平方的平均值，从而实现学习率的自适应调整。RMSProp算法为：

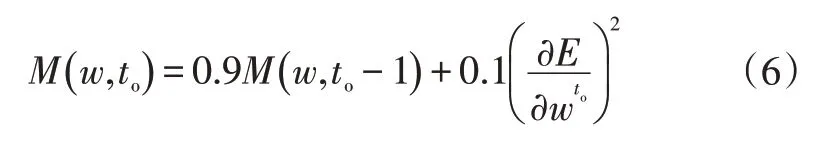
式中，w为深度神经网络的工作权重；to为训练的步骤；为训练步骤to中w的梯度。

输入层数据包括车辆速度、加速度、偏航角速度、转向角和道路曲率等车辆状态信息。输出层有6个节点，分别对应后续1 s、2 s、3 s处的纵向预测和横向预测，采用Leaky ReLU激活函数。隐藏层的数量设置为5，神经元的数量设置为200，小批量数量设置为128，学习率设置为0.1，迭代次数设置为100。

2.3 ELM网络设计

ELM[18]具有强大的网络概括性，其模型输入矩阵X和输出矩阵Y假定为：

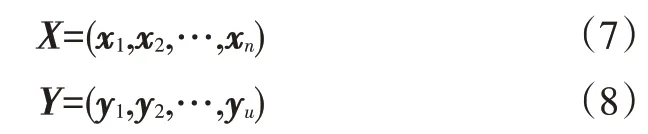
假设隐藏层激活函数为g(x)，隐藏层神经元的数量为1，网络输出T为：

式中，ti为网络输出；l为隐藏层节点的个数；为连接隐藏层与输出层的输出权重；bj为隐藏层偏置；为第K个输入层与隐藏层之间的权值；g(ωj,bj,xi)为第i个隐藏层神经元的输出。

式（11）可表示为T=Hβ，其中H为隐藏层输出矩阵[18]，β可以通过最小二乘估计，即=H+T，H+为H的Moore-Penrose 广义逆，T由训练样本输出Y代替。

粒子群优化（Particle Swarm Optimization，PSO）的本质是搜索最佳位置，并通过迭代找到全局最优解。假设粒子群位置和速度是S维向量，则更新公式为：

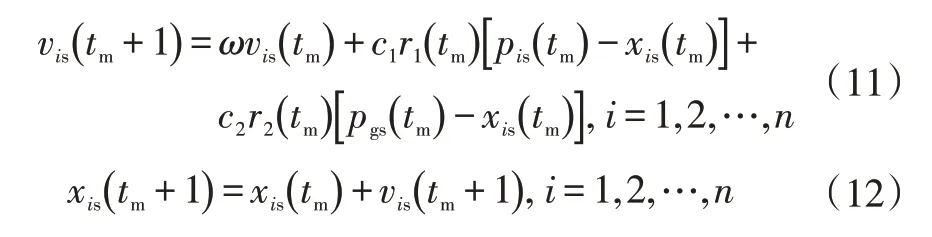
式中，tm为迭代的步骤；vis、xis分别为第i个粒子的速度和位置；c1和c2分别为粒子群学习因数；r1、r2为[0,1]范围内的随机数；pis为目前个体的最优极值；pgs为目前的全局最优极值；ω为功率常数。

ω较大时，全局搜索能力强，但很容易跳过最优解；ω较小时，局部搜索能力强，但很容易陷入局部最优解，并且收敛缓慢。因此，本文提出了一种基于模拟退火粒子群算法的改进的ω自适应公式：

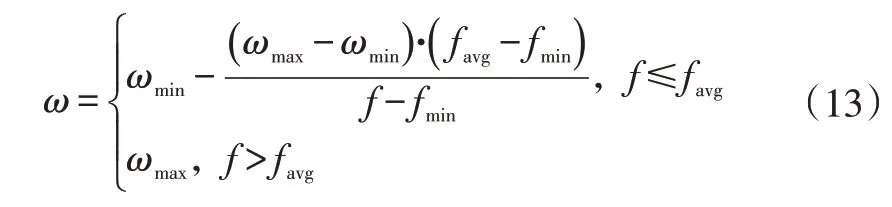
式中，ωmin和ωmax分别为功率常数的最小值和最大值；f为粒子的当前个体适应度；fmin为整个粒子群的最小适应度；favg为整个粒子群适应度的当前平均值。

设粒子群算法迭代次数为50、群体个体数量为100、学习因子c1和c2均为1.539 2，设ωmin=0.4、ωmax=0.9，激励函数为S 型函数，隐藏层神经元的数量为15。ELM 输入权重矩阵和隐藏层阈值由随机算法给出，通常需要更多隐藏层神经元才能达到理想的预测精度。测试集均方误差被认为是适应度函数，利用SAPSO 算法可以提高ELM 模型的随机性，因此ELM 只需要少量隐藏层神经元便可以获得更好的预测效果，改善网络泛化的问题。

3 仿真与验证

3.1 联合仿真

为了验证基于信息融合的深度神经网络的轨迹预测的性能，使用PreScan 和MATLAB/Simulink 构建了仿真环境。从车辆驾驶模拟中获得了用于学习和验证的必要数据集，从模拟试验收集了车辆状态信息，同时在真实数据集Lankershim Boulevard Dataset 上进行了验证。车辆状态信息包括车速、加速度、偏航角速度、车轮转向角和道路曲率。

为评估本文提出的车辆轨迹预测方法的可靠性，针对每个预测项计算均方误差（Mean Square Error，MSE）和标准偏差（Standard Deviation，Std Dev）。使用70%的模拟数据进行训练，另外20%用于验证，其余10%用于测试。用于测试的数据集是在2 条弯曲道路组成的单独模拟驾驶场景中收集的。仿真场景如图2所示，车速设定为72 km/h。

图2 模型结构

3.2 验证分析

实际车辆轨迹以及测试场景的预测结果如图3 所示，预测在1 s之后进行。

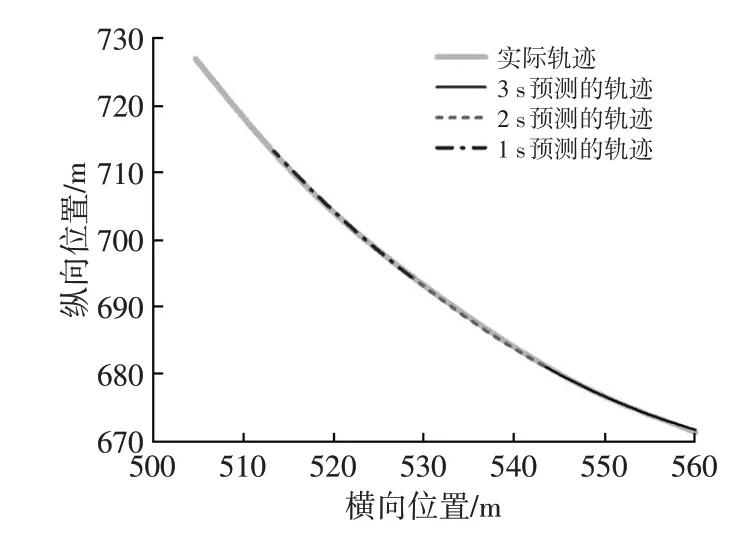
图3 车辆轨迹的实际位置与预测位置

将本文提出的方法与3 层隐藏层的人工神经网络（Artificial Neural Network，ANN）、ELM、DNN 等数据驱动的预测方法进行比较，轨迹预测结果的均方误差、标准偏差如表1 所示，基于动态时间规整（Dynamic Time Warping，DTW）的相似度计算结果如表2所示。

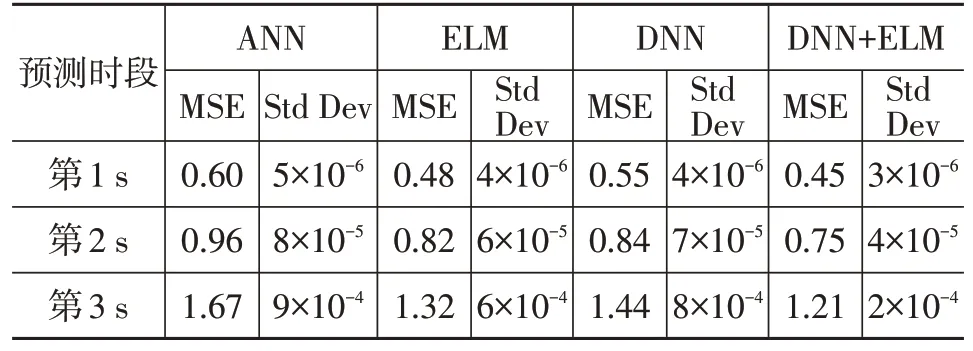
表1 不同算法的轨迹预测可靠性

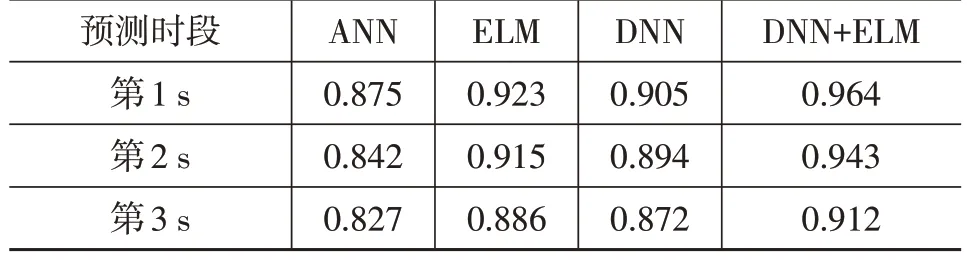
表2 不同方法的轨迹相似度

两条轨迹间的相似度Sm用公式表示为：

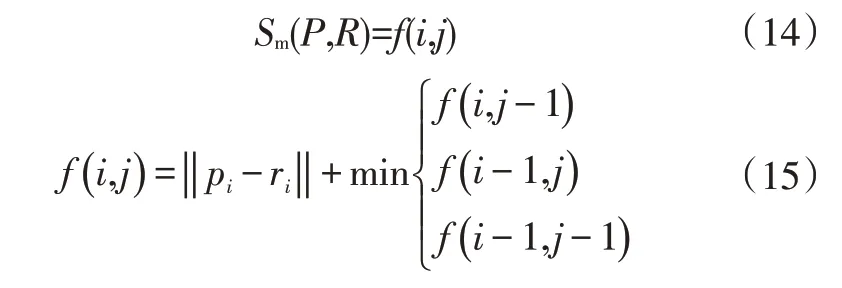
式中，‖· ‖ 为两点坐标的二范数，即欧氏距离；P、R分别为两条轨迹相应点的集合；pi、ri分别为对应的点的坐标。

将所提出的DNN+ELM 方法在真实数据集Lankershim Boulevard Dataset 上进行验证，该数据收集区域的长度约为500 m，包括3～4个车道，并完全覆盖3个信号交叉口。数据是由安装在毗邻美国101 号高速公路和Lankershim 大道的36 层建筑物屋顶上的5 个摄像机获得的。该方法与基于物理的运动模型、高斯过程回归（Gaussian Process Regression，GPR）在3 种场景下左转、右转、直行的预测结果如图4所示，轨迹中前10个位置用于对模型进行训练，误差范围如图5所示。

与其他模型相比，本文提出的融合模型在1 s、2 s、3 s的预测更精准。该结果表明，采用基于融合的深度神经网络的车辆轨迹预测可以用于风险评估和驾驶辅助。

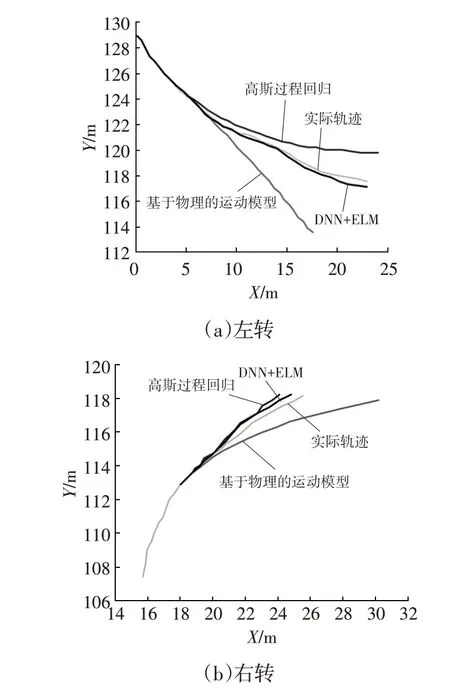
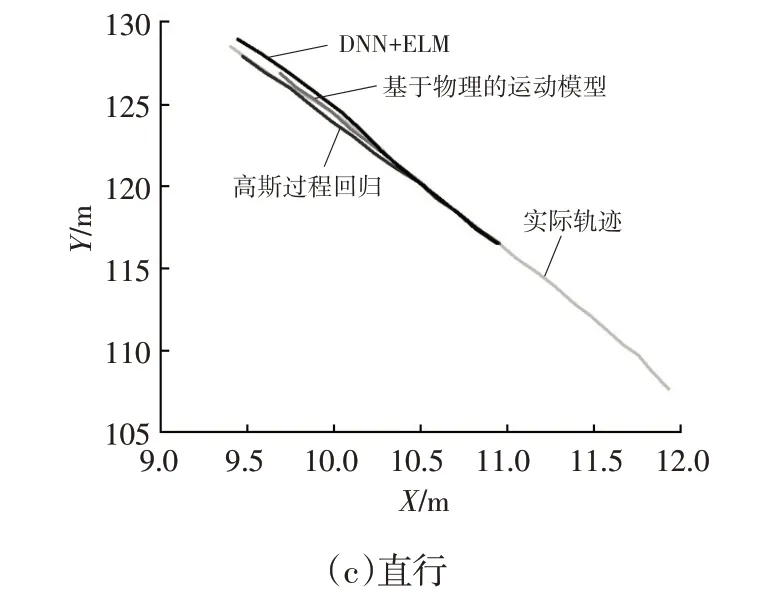
图4 不同方法在真实数据集上的预测结果

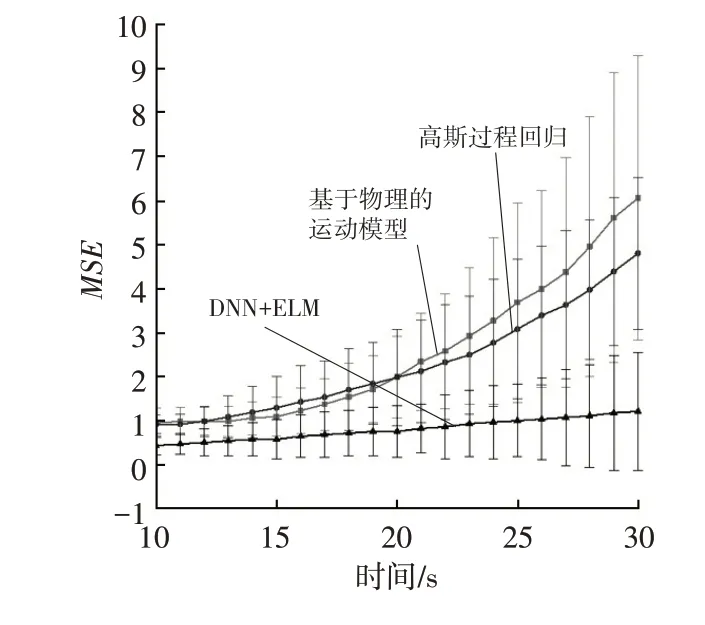
图5 3种方法误差范围的比较

4 结束语

本文提出了一种基于改进极限学习机和深度神经网络融合的车辆轨迹预测方法，改进的极限学习机以模拟退火粒子群优化算法为基础，改进的深度神经网络使用修正线性单元函数替换激活函数，并使用均方根反向传播算法来优化深度神经网络。模拟结果验证了该方法在道路曲率变化工况下的可行性。在未来的工作中，该方法将扩展到基于周围环境中其他车辆进行轨迹预测，以及碰撞检测和警告算法的研究。