一种求解Euler方程的高阶格式

任琴琴, 郑秋亚, 梁益华

(1. 长安大学 理学院, 西安 710064； 2. 中国航空计算技术研究所 航空气动力数值模拟重点实验室, 西安 710068)

在计算流体力学中, 许多经典的数值方法已被广泛应用. 一个好的数值方法应该在光滑区域获得较高的精度, 同时在间断附近避免非物理意义的伪振荡. Liu等[1]提出了加权本质无振荡(WENO)方法, 并构造了三阶WENO格式. 目前, WENO格式在数值模拟中已成为求解非线性双曲守恒律方程常用的数值方法之一, 但WENO格式计算量大、 数值耗散偏大. Jiang等[2]在多维空间上建立了具有一般平滑因子和非线性权重的五阶WENO-JS格式; Henrick等[3]对WENO-JS进行分析表明, 在临界点处并未达到最优解, 利用映射函数提出了WENO-M格式; 文献[4-6]进一步分析改进并提出了WENO-Z格式, 这两种格式主要改进了WENO-JS格式中的非线性权重, 从而在一定程度上降低了耗散, 提高了分辨率; 文献[7-8]通过引入一种基于Lagrange插值的新局部光滑因子η, 并给出η的显式表达式, 构造了WENO-η格式.

为提高计算效率, 在间断处达到高分辨率, 研究者们又提出了对流迎风分裂(AUSM)格式[9]与对流迎风和分压(CUSP)格式[10]. 根据其物理性质, AUSM格式将无黏通量分裂为对流项和压力项, CUSP格式根据其对流项的物理特征, 分为总焓对流迎风和分压(H-CUSP)格式[11]与总能对流迎风和分压(E-CUSP)格式[12-15]. 两种格式计算过程中都避免了矩阵运算, 简化格式的同时提高了计算效率. E-CUSP格式从Jacobi矩阵的特征值出发, 分裂得到对流项和压力项. 通过将无黏通量分解为守恒型通量和压力型通量构造通量. 该格式扩散小, 能清晰捕捉激波和接触间断. 本文在空间上采用E-CUSP格式与WENO-η格式耦合得到一种新格式, 时间上采用4阶TVD Runge-Kutta方法[16].

1 控制方程

1.1 Euler方程

考虑一维标量双曲守恒律方程:

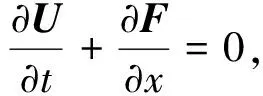
(1)

其中：U=(ρ,ρu,E)T为守恒变量,F=(ρu,ρu2+p,(E+p)u)T为通量,ρ表示密度,u表示速度,E表示单位体积的内能,p=(γ-1)(E-ρu2/2)表示压强,γ=1.4表示比热比;t表示时间变量；x表示空间变量.

1.2 E-CUSP格式

在区间单元上利用有限体积法, 可得方程(1)的数值离散形式为

(2)

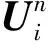
E-CUSP格式[15]的主要思想是通量分裂数值耗散项的系数不是矩阵而是标量, 避免了矩阵运算, 提高了计算效率.

式(1)中F的Jacobi矩阵为

其中，

a为音速,H=(E+p)/ρ为总焓.

F与A之间的齐次性关系式为

F=TΛT-1U.

(3)

根据Jacobi矩阵特征值的特性, 将式(3)拆分可得

其中：Fc=u(ρ,ρu,E)T为守恒型通量；Fp=(0,p,pu)T为压力型通量. 因此，通量F可表示为守恒型通量Fc与压力型通量Fp之和. 通量Fc可表示为

其中Uc=(1,u,E/ρ)T. 在交界面处质量通量的表达式为(ρu)1/2=(ρLuL+ρRuR), 其中速度uL和uR定义如下：

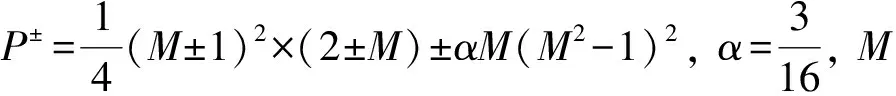
因此, E-CUSP格式中通量F可表示为

2 数值方法

2.1 WENO-JS格式数值重构

WENO格式用于评估变量UL和UR. 采用qk的凸组合近似变量UL的WENO格式, 可写成

(5)

其中:qk(k=0,1,…,r-1)是不同模板中变量的重构多项式;γk(k=0,1,…,r-1)是权重.

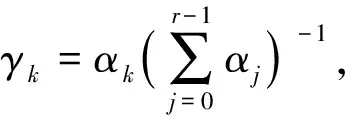
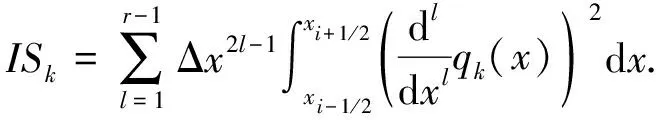
(6)

对七阶(r=4)WENO-JS格式, 有

2.2 WENO-η格式数值重构

类似上述光滑因子的构造过程, Fan等[7]基于Lagrange插值多项式重新定义了一种新的局部光滑因子, 该光滑因子η的简洁公式为

(7)

(8)

由ηk重构的新WENO格式, 记为WENO-η.

因此, 根据式(7)和式(8)计算出对于七阶(r=4)的WENO-η格式, 新光滑因子ηk可表示为

(9)

显然, 式(9)中ηk的显式表达式比七阶的WENO-JS格式中ISk的表达式更紧凑. 通过Lagrange插值多项式Pi,r(x)的Taylor展开式, 可观察到Lagrange插值多项式有以下递归关系：

(10)

根据式(10), 易从低阶的插值多项式递归导出更高阶的插值多项式, 利用该性质可很大程度简化更高阶光滑因子ηk显式表达式的推导过程.

类似文献[4-6]中WENO-Z格式非线性权重定义的思想： 利用经典的局部光滑因子IS构造高阶全局光滑指标τ2r-1, 使得WENO-Z权值的凸组合比WENO-JS更接近于中心格式, 从而减少耗散. WENO-η也可构造一系列的全局光滑因子.

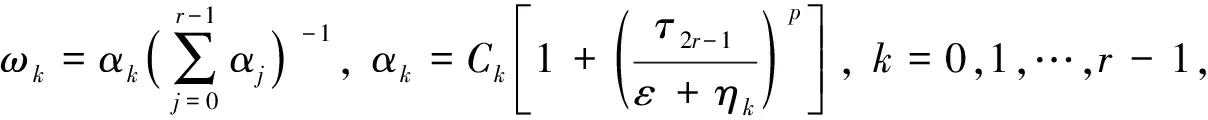
而且基于η的对称性, 分析ηk的Taylor级数展开式可得τ2r-1的截断误差为τ2r-1=ο(Δxr+2).

2.3 高阶全局光滑指标τ2r-1的改进

除给出全局光滑性因子τ2r-1的规则形式外,τ2r-1也可用如下方法[8]表示:

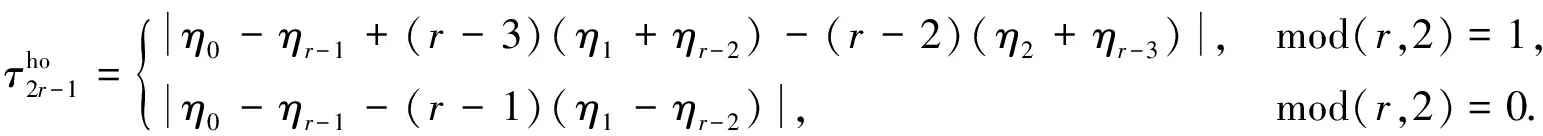
(11)

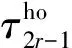
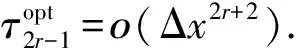
(12)

其中Fk(k=1,2,…,r-1)的表达式为

2.4 Runge-Kutta方法

对Euler方程在时间方向上的离散, 本文利用如下4阶TVD Runge-Kutta方法[16]:

求解

(13)

其中： Δt表示计算的时间步长；L(·)表示差分算子.

3 数值结果与分析

其中:y(xj)为方程的数值解;y(x)为方程的精确解. 对比不同格式的数值模拟结果, 从而分析其性能.

3.1 一维Euler方程激波管问题

例1在区域[0,1]上求解初值问题:

3.2 一维Euler方程Lax激波管问题

例2在区域[0,1]上求解初值问题:

图1 一维Euler方程激波管问题的数值解Fig.1 Numerical solution of shock tube problem for one-dimensional Euler equation

图2 一维Euler方程Lax激波管问题的数值解Fig.2 Numerical solution of Lax shock tube problem for one-dimensional Euler equation

综上, 首先本文基于Riemann问题解求解一维Euler方程, 在已有WENO格式的基础上通过重新构造基于Lagrange插值多项式的局部光滑因子和全局光滑因子, 改变非线性权值构造过程, 构造出高阶WENO-η格式. 与其他经典WENO格式相比, WENO-η格式收敛阶数更高. 其次, 本文考察了低耗散 E-CUSP格式与高阶精度WENO-η格式的耦合性能. 在相同网格条件下, 理论分析和数值实验结果表明, 新格式对接触间断和激波的捕捉更精确, 分辨率和计算精度均更高, 数值耗散更小. 因此, 新格式具有更好的稳定性.

表1 不同格式求解例1和例2的相对误差对比