多孔介质中Brinkman-Forchheimer模型的结构稳定性

石金诚, 李远飞

(广东财经大学华商学院 数据科学学院, 广州 511300)

1 引言与预备知识

目前, 关于多孔介质中流体方程组结构稳定性的研究已有很多结果[1-21], 但这些研究大多数只考虑了方程的结构稳定性, 而忽略了方程的收敛性结果. 文献[6]研究了溶解度与温度有关的Brinkman-Forchheimer流体方程组的结构稳定性, 其控制方程组为

(1)

其中:ui,p,T,C分别表示速度、 压强、 温度和盐浓度;gi(x)和hi(x)分别表示引力向量函数, 假设gi满足|gi|≤G1和|gi|≤G2,hi满足|hi|≤H1和|hi|≤H2； Δ为Laplace算子；λ,L和k均是大于零的常数. 方程组(1)在Ω×[0,τ]内成立, 其中Ω是3中一个有界单连通的星形区域,τ是给定的常数且0≤τ<∞. 方程组(1)是一种基于动量守恒、 质量守恒、 能量守恒和盐浓度守恒的方程组, 是在动量方程中采用Forchheimer逼近而得到的方程组, 其边界条件为

(2)

初始条件为

ui(x,0)=ui0(x),T(x,0)=T0(x),C(x,0)=C0(x),x∈Ω.

(3)

2 先验估计

引理1温度T和盐浓度C满足如下最大值估计：

(4)

(5)

证明: 在方程组(1)中第三个方程两边同时乘以2rT2r-1(r≥1), 并在Ω×[0,t](t∈[0,τ])上积分, 可得

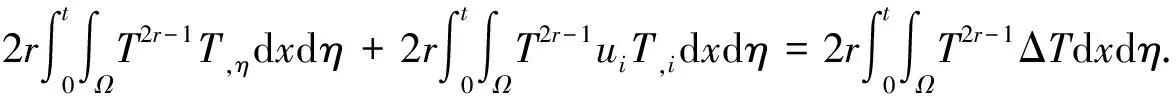
(6)

对式(6)等号左边第二项, 由散度定理和式(2)可得

(7)

对式(6)等号右边项, 由散度定理、 Young不等式和式(2), 可得

联合式(6)～(8), 可得

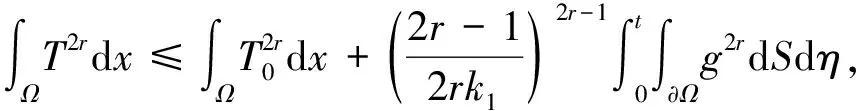
(9)

将式(9)两边同时在[0,t]上积分, 可得

(10)

当r→+∞时, 有

(11)

在方程组(1)中的第四个方程两边同时乘以2rC2r-1(r≥1), 并在Ω×[0,t](t∈[0,τ])上积分, 可得

对式(12)等号右边第一项, 由散度定理、 Young不等式和式(2), 可得

(13)

对式(12)等号右边第二项, 由Young不等式可得

(14)

联合式(12)～(14), 可得

(15)

将式(15)两边同时在[0,t]上积分, 可得

当r→+∞时, 有

(17)

引理2对温度T和盐浓度C, 有下列估计:

(18)

(19)

其中:

证明: 在方程组(1)中第三个方程两边同时乘以2T并在Ω×[0,t]上积分, 可得

(20)

由式(20)可知

(21)

同理, 在方程组(1)中第四个方程两边同时乘以2C并在Ω×[0,t]上积分, 可得

(22)

由式(22)可知

(23)

其中|Ω|是Ω的体积.

3 连续依懒性

(24)

边界条件为

(25)

初始条件为

ωi(x,0)=0,θ(x,0)=0,φ(x,0)=0,x∈Ω.

(26)

(27)

证明: 将方程组(24)中第一个方程两边同时乘以2ωi并在Ω上积分, 可得

对式(28)等号右边第一项, 有

(29)

对式(28)等号右边第二项, 由散度定理和式(25), 可得

(30)

联合式(28)～(30), 可得

(31)

将方程组(24)中第三个方程两边同时乘以2θ并在Ω上积分, 可得

(32)

对式(32)等号右边第一项, 由散度定理和式(25), 可得

(33)

对式(32)等号右边第二项, 由散度定理和式(25), 可得

(34)

联合式(32)～(34), 可得

将方程组(24)中第四个方程两边同时乘以2φ并在Ω上积分, 可得

(36)

对式(36)等号右边第一项, 由散度定理和式(25), 可得

(37)

联合式(36),(37), 可得

联合式(31),(35),(38), 可得

(40)

由式(18),(19)和Gronwall不等式, 可得

(41)

4 收敛性

(42)

边界条件为

(43)

初始条件为

(44)

假设(ωi,θ,φ,π)满足下列方程组:

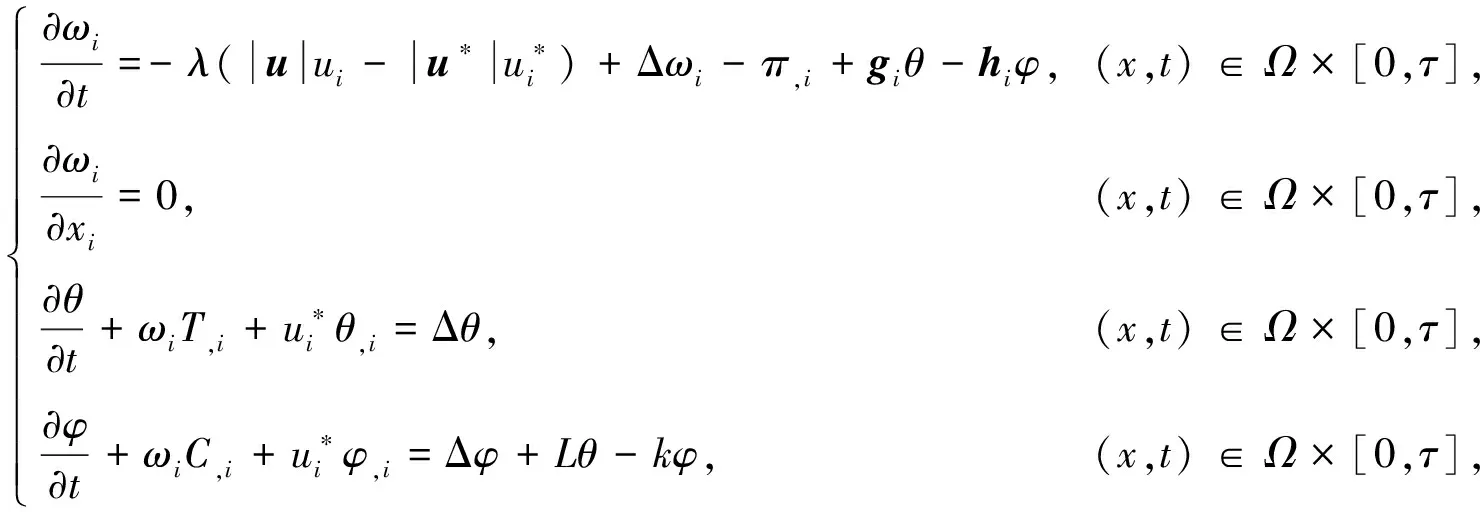
(45)

边界条件为

(46)

初始条件为

ωi(x,0)=0,θ(x,0)=0,φ(x,0)=0,x∈Ω.

(47)

引理3对连续且偏导数存在的函数ω=ω(x,t), (x,t)∈Ω×[0,τ], 有下列估计：

(48)

证明: 对任意函数ω=ω(x,t), (x,t)∈Ω×[0,τ], 由散度定理有

(49)

(50)

对式(50)利用Schwarz不等式, 可得

(51)

由式(51)即可得式(48).

引理4对温度T*和盐浓度C*, 有下列估计：

(52)

(53)

其中n3(t),n4(t)均为单调递增且大于零的函数.

证明: 在方程组(42)中第三个方程两边同时乘以2T*并在Ω×[0,t]上积分, 可得

(54)

由式(43),(48), 可得

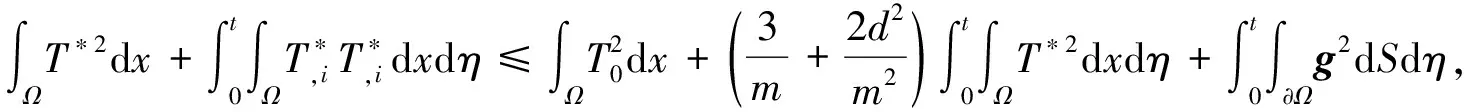
(55)

将式(55)两边同时在[0,t]上积分, 可得

(56)

将式(56)代入式(55), 可得

联合式(56),(57),(48)可得式(52), 其中

同理可得式(53), 其中n4(t)是可计算且大于零的函数.

引理5对温度T*和盐浓度C*, 有下列估计：

(58)

(59)

其中n5(t),n6(t)均为单调递增且大于零的函数.

证明: 在方程组(42)中第三个方程两边同时乘以4T*3并在Ω×[0,t]上积分, 可得

利用式(48), 可得

(61)

求解式(61)得

(62)

将式(62)代入式(61)可得式(58), 其中

同理可得式(59), 其中n6(t)是可计算且大于零的函数.

(63)

其中m2,γ均为大于零的常数.

证明: 将方程组(45)中第一个方程两边同时乘以2ωi并在Ω上积分, 可得

(64)

将方程组(45)中第三个方程两边同时乘以2ωi并在Ω上积分, 由散度定理和式(46), 可得

将方程组(45)中第四个方程两边同时乘以2φ并在Ω上积分, 可得

(66)

对式(66)等号右边第一项, 由散度定理可得

由式(66),(67), 可得

联合式(64),(65),(68), 对任意正常数γ, 有

利用文献[22]中结果(B.17), 可得

(70)

令

则有

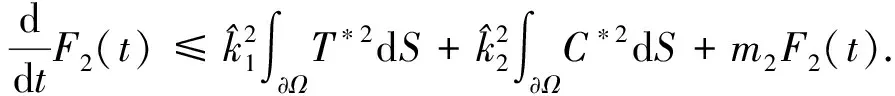
(71)

由式(52),(53)和Gronwall不等式, 可得

(72)