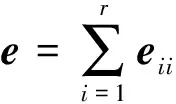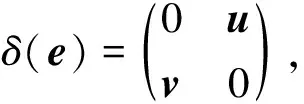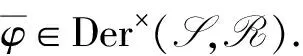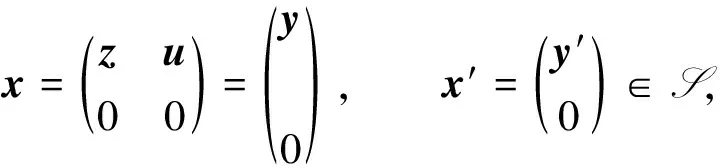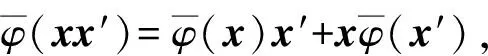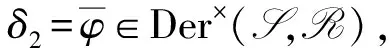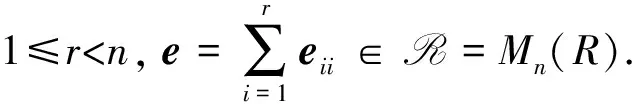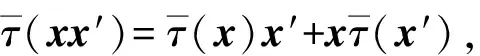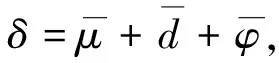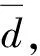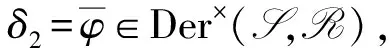矩阵环的乘法导子

王灵燕, 徐晓伟

(吉林大学 数学学院, 长春 130012)

设R是环, 如果对任意的x,y∈R, 均有f(xy)=f(x)f(y), 则称映射f: R→R为R上的乘法映射； 如果对任意的x,y∈R, 均有δ(xy)=δ(x)y+xδ(y)，则称映射δ: R→R为R上的乘法导子. 映射f: R→R是R的自同构当且仅当f是R上的乘法双射, 且是加性映射; 映射δ: R→R是R上的导子当且仅当δ是R上的乘法导子, 且是加性映射.

目前, 关于环上乘法双射是加性映射的研究已有很多结果： 文献[1]和文献[2]分别给出了环上乘法双射是加性映射(同构)的充分条件; 文献[3]从幂等元的角度给出了环上乘法双射是加性映射(同构)的充分条件; 文献[4]改进了文献[3]的结果； 文献[5]研究了环上的乘法导子, 证明了当有单位元1的结合环R满足如下条件时, R上的乘法导子是加性映射(R上的导子): R的左零化子为零, 且有幂等元e≠0,1, 使得eR的右零化子是零, 且对任意x∈R, 若exeR(1-e)=0, 则必有exe=0. 注意到当n≥2时, 有单位元1的结合环上的n阶矩阵环满足上述条件, 因此其上的乘法导子是导子； 文献[6]研究了拓扑空间X上的全体实(复)连续函数构成的代数R=C(X)上的乘法导子, 并当X满足一定条件时, 给出了R=C(X)上乘法导子的结构; 文献[7]研究了交错环上乘法导子是加性映射(导子)的条件; 文献[8]给出了含非平凡幂等元的素环R上导子的一个判别条件, 并证明了如果映射δ: R→R 满足对任意(x,y)∈A ⊆R×R, 有δ(xy)=δ(x)y+xδ(y), 则δ是导子, 其中

A={(x,y)∈R×R|([x,y]y)2=0};

文献[9]定义了环到其上双模的乘法导子: 设M是环R上的双模, 如果对任意x,y∈R, 有δ(xy)=δ(x)y+xδ(y), 则称映射δ:R→M为乘法导子, 并证明了当R含有一个满足6个条件的幂等元时, 则R到其双模M的乘法导子是加性的.

设S是环R的乘法闭子集, 即对任意x,y∈S, 总有xy∈S. 如果对任意x,y∈S, 总有δ(xy)=δ(x)y+xδ(y), 则称映射δ: S →R为乘法导子. 上述研究表明, R上的导子限制在S上是S到R的乘法导子, 但不确定S到R的乘法导子是否为R上导子的限制. 文献[10]证明了当R是二元域上的2阶矩阵环, S为全体可逆矩阵构成的乘法闭子集时, 乘法导子δ: S →R是R上导子的限制.

本文考虑一般的有单位元1的结合环R上的n阶矩阵环R=Mn(R), 研究其乘法闭子集S到R的乘法导子, 给出S =eR到R乘法导子的结构, 这里e为对角线上前r个元素均为1, 其余元素均为0的n阶对角矩阵, 1≤r

例1设为实数域, R=M2(),定义映射δ: S →R, 使得

易验证δ是乘法导子, 但不是加性映射.

因为本文考虑的R的乘法闭子集S恰为R的子环, 因此R也可视为环S上的双模, 从而本文所讨论的问题也可置于文献[9]的框架下, 但例1表明S到R的乘法导子一般不是加性的, 即文献[9]的结论不能涵盖本文的结论.

设R是环,r,s是正整数,Rr×s表示R上全体r×s矩阵构成的集合. 特别地, 可用Ms(R)表示Rs×s, 此时Ms(R)也是环, 称为R上的s阶矩阵环. 用I表示单位矩阵,eij表示(i,j)分量为1、 其余分量均为0的矩阵单位, 其阶数为其所在矩阵环的阶数.

设R是环, 对于x,y∈R, 记[x,y]=xy-yx. 对于x0∈R, 用ad(x0)表示由x0诱导的R的内导子, 即对任意的x∈R, 有ad(x0)(x)=[x0,x]. 若τ是R上的导子, 则对正整数n,τ诱导了一个Mn(R)上的导子τn, 使得

设R是环,M,N都是左R模, 如果对任意a∈R及任意x∈M, 都有f(ax)=af(x), 则称f:M→N是左R映射. 如果左R映射f还是加性映射，则f是左R模同态. 因此, 左R映射可理解为左R模同态的弱化. 用Der×(S,R)表示S到R全体乘法导子构成的集合.

引理1设R是环, S是R的乘法闭子集, Z是R的中心, 则Der×(S,R)是Z-模.

证明: 因为Map(S,R)={f|f是S到R的映射}是Z-模, 且Der×(S,R)是Map(S,R)的非空子集. 因此, 只需证Der×(S,R)是Map(S,R)的子模, 即只需证Der×(S,R)关于加法和纯量乘法都封闭, 从而只需证对任意δ1,δ2∈Der×(S,R)和任意的λ1,λ2∈Z, 都有

λ1δ1+λ2δ2∈Der×(S,R).

事实上, 对任意x,y∈S, 有

表明λ1δ1+λ2δ2∈Der×(S,R), 结论得证.

引理2设n,r是整数, 且满足1≤r

证明: 由文献[11]中定理2知, 存在z0∈Mr(R)及R上的导子τ, 使得

μr=ad(z0)+τr,

这里τr表示τ诱导的Mr(R)上的导子. 令μn=ad(x0)+τn, 其中:τn表示τ诱导的Mn(R)上的导子;

则

证毕.

1) 当1

δ(x)=(μ(z)+d(z))e11.

δ(e)=δ(e2)=δ(e)e+eδ(e).

(1)

将式(1)两边同时左右乘e, 得eδ(e)e=2eδ(e)e, 则eδ(e)e=0. 将式(1)两边同时左右乘(1-e), 得

(1-e)δ(e)(1-e)=0.

表明

其中:u∈Rr×(n-r);v∈R(n-r)×r. 令

则ad(B)(e)=[B,e]=δ(e). 由ad(B),δ∈Der×(S,R)及引理1知,

δ1=δ-ad(B)∈Der×(S,R),

且δ1(e)=0. 对任意z∈Rr×r, 由δ1(e)=0知

从而存在映射μr:Mr(R)→Mr(R), 使得

进一步, 对任意z,z′∈Mr(R), 有

表明μr∈Der×(Mr(R),Mr(R)).

当1

证明: 任给

其中：z∈Rr×r;u∈Rr×(n-r);y,y′∈Rr×n. 则一方面, 有

另一方面, 有

从而对任意x∈S, 有δ2(x)=δ2(ex)=eδ2(x), 即δ2(x)∈S. 进而有eδ2(x)e=δ2(exe)=0, 即

其中u∈Rr×(n-r). 于是有映射φ:Rr×n→Rr×(n-r), 使得

对任意z∈Rr×r,y∈Rr×n, 有

必要性得证. 证毕.

证明: 对任意的

一方面, 有

另一方面, 有

定理2设n>1是整数,R是有单位元1的结合环, S =e11R ⊆R=Mn(R)是R的乘法闭子集. 则δ∈Der×(S,R)当且仅当存在R上的导子μ和R上的乘法导子d以及左R映射φ:R1×n→R1×(n-1), 使得

即

从而对任意x∈S, 有δ2(x)=δ2(e11x)=e11δ2(x), 即δ2(x)∈S. 进而有e11δ2(x)e11=δ2(e11xe11)=0, 即

其中u∈R1×(n-1). 于是有映射φ:R1×n→R1×(n-1), 使得

对任意z∈R,y∈R1×n, 有

必要性得证. 证毕.