如何正确运用Z检验——Z检验的基本概念与前提条件

胡良平

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

在对多种统计量进行比较时需要用到Z检验，本文将着重介绍“与Z检验有关的基本概念”“正态分布与其他概率分布之间的关系”和“正态分布可用于某些其他概率分布的近似计算”这三部分内容。

1 与Z检验有关的基本概念

1.1 何为Z检验

以正态分布为理论依据的假设检验叫做Z检验。Z只是一个符号或名称，它本身并无特殊含义，关键是它所表达的内容。例如，当人们收集了来自单组设计一元定量资料（设结果变量名为“x”）的n个取值时，将其代入下面的式（1）进行计算，再依据正态分布的理论和方法，就可以推断这个样本所代表的总体均值与已知均值“μ0”之间的差别是否具有统计学意义。

在式（1）中，假定“标准差σ”是一个已知的常数。由此式所定义的“Z”被称为“Z检验统计量”，即它是一个可用于实现对某种“检验假设”进行检验的计算公式。统计学家已经证明，式（1）中定义的“Z检验统计量”是一个服从标准正态分布的随机变量，故可以基于样本数据代入式（1）计算出来的结果，并依据标准正态分布的理论作出统计推断。在统计学中，类似式（1）的公式还有多个（注意：应用场合和公式的具体表现形式不尽相同），因篇幅所限，此处从略。

1.2 何为正态分布

1.2.1 正态分布的历史

早在1733年，A.de Moivre首先提出这种分布的方程，至19世纪初期，德国数学家C.F.Gauss与法国数学家P.S.de Laplace分别对其加以发展，但他们过分强调一切自然现象均服从正态分布。约在1924年后，经英国数学家K.Pearson论证，正态分布只是自然界中随机变量的一种分布形式［1-3］。因此，把“正态”作为分布的一种名称而不作为“正常状态”来理解，更为合适。

1.2.2 正态分布的作用

纵观经典统计学的全部内容，正态分布在统计学理论中确实占有十分重要的地位，因为它具有许多良好的性质，是许多分布（如二项分布、Poisson分布、t分布、χ2分布、F分布等）在特定条件下的近似分布；另一方面，有一些重要分布（如χ2分布、t分布、F分布及其非中心分布）是由正态分布派生而来。一般情况下，若影响某一数量指标的随机因素很多，而每个因素所起的作用不太大，则这个指标的取值近似服从正态分布。

1.2.3 一般正态分布的定义

若连续型随机变量x的概率密度函数由下面的式（2）给出：

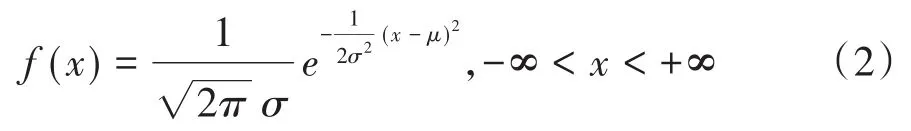
则称x服从一般正态分布，并记作x～N（μ，σ2），其分布函数（也称为累积概率分布函数）见式（3）：

1.2.4 标准正态分布的定义

由上文中的一般正态分布可知，每个实际问题对应着一个特定的“概率密度函数（由具体的均值μ和方差σ2）”所决定。在解决实际问题时，每次都可能要涉及式（2）或式（3）的复杂计算。为了简化计算，可通过式（4）将一般正态分布转变成标准正态分布：

由式（4）可以解出变量x，见下面的式（5）：

将式（5）中等号右边的内容代入式（2）和式（3）等号右边，就得到式（6）和式（7）：

在式（6）和式（7）中，“Z”被称为服从标准正态分布的随机变量，简记为Z～N(0，1)，其含义是：服从标准正态分布的随机变量Z的均值为“0”、方差为“1”；式（6）和式（7）分别被称为“标准正态分布的概率密度函数”和“标准正态分布的累计分布函数”。

1.2.5 正态分布曲线下的面积与横坐标之间的关系

若x～N（μ，σ2），则有式（4）成立，且有下面的诸关系式成立：

上面的三个式子表明：标准正态分布随机变量Z分别在区间［-1，1］、［-1.960，1.960］和［-2.576，2.576］内取值的概率分别为0.683、0.950和0.990。即只要人们知道某个实际问题中“Z”的取值，就可以近似知道Z在某个特定区间上取值的近似概率。例如，在某个实际问题中，已知Z～N(0，1)且Z=2.003，若再做类似的重复试验，出现“Z＞2.0”或“Z＜-2.8”的结果也是有可能的，据此，提出下面两个问题：

问题1：“Z＞2.0”的概率是多少？

问题2：“Z＜-2.8”的概率是多少？

【回答】对问题1而言，依据式（9）可知：P（Z＞1.960）＜5%/2=2.5%，故P（Z＞2.0）＜2.5%；对第 2个问题而言，依据式（10）可知：P（Z＜-2.576）＜1%/2=0.5%，故P（Z＜-2.8）＜0.5%。

欲求出“P（Z＞2.0）”或“P（Z＜-2.8）”的精确数值，必须利用式（6）和式（7）进行计算，因篇幅所限，此处从略。

1.3 Z检验的前提条件

Z检验的前提条件不便一概而论，取决于针对不同实际问题所构造的“Z检验统计量”。就前面式（1）而言，一般要求结果变量x是定量的且近似服从正态分布，样本含量n不应过小，至少需为30。其他的“Z检验统计量”，其前提条件要视具体情况而定，此处从略。

1.4 Z检验的适用场合

1.4.1 均值比较

服从正态分布计量资料且总体方差已知时两算术均值比较、服从Poisson分布计数资料两均值比较、服从偏态分布计量资料两平均秩比较的近似检验和定量资料Meta分析中的效应指标（标准化均值差）的比较，均可以运用Z检验。

1.4.2 率比较

两个一般率比较常用χ2检验，但在一定条件下，也可以运用Z检验；在对两个率进行非劣效性检验、等效性检验和优效性检验时，需要采用Z检验。

1.4.3 同类的一般统计量比较

例如：两个偏度系数的比较、两个峰度系数的比较、两个Kappa（一致性）系数的比较和定性资料Meta分析中的效应指标（如相对危险度）的比较。需注意，这里所说的“两个”通常指：一个是一般统计量来自未知总体，其取值是基于样本数据计算而得，而另一个则属于一个已知总体中相应的数值，即参数（如假定已知总体的偏度系数为0、假定已知总体的Kappa系数为0）。

1.5 Z分位数的适用场合

设Z是一个服从标准正态分布的随机变量，则标准正态分布曲线下横坐标上的任何一个刻度值都叫做一个“Z分位数”。例如，Z0.005=-2.576、Z0.025=-1.960、Z0.5=0；或Z0.975=1.960、Z0.995=2.576。Z的下角标代表标准正态分布曲线下左侧尾端的面积（本质上为“概率”）。在统计学上，常利用分位数“Z0.975=Z1-0.05/2=1.960”来构建服从正态分布的定量资料总体均值双侧95%置信区间，见下式：

常利用分位数“Z0.995=Z1-0.01/2=2.576”来构建服从正态分布的定量资料总体均值双侧99%置信区间，见下式：

2 正态分布与其他概率分布之间的关系

2.1 正态分布是t分布的极限分布

设t分布的概率密度函数为t(x，n)，则它的表达式如下［4-5］：

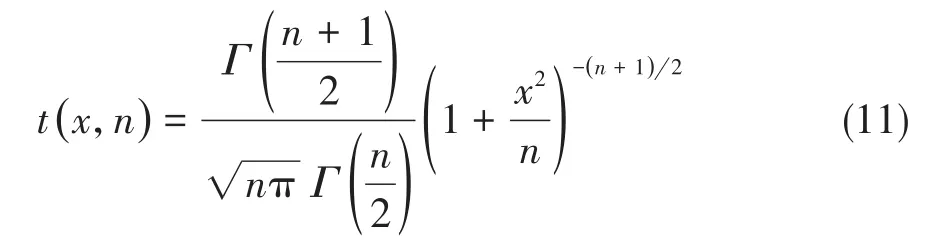
基于高等数学知识，可得下式：

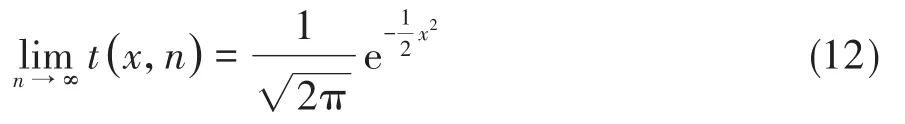
式（12）的含义是：在“n→ ∞”的条件下，t分布的概率密度函数的极限形式是标准正态分布概率密度函数，基于此式，数学上就称为“正态分布是t分布的极限分布”。

2.2 正态分布是其他几种分布的极限分布

基于高等数学知识和中心极限定理知识等，可推导出如下结果：正态分布是χ2分布、F分布、二项分布、Poisson分布的极限分布，为节省篇幅，公式从略。

3 正态分布可用于某些其他概率分布的近似计算

由前述可知，正态分布是t分布、χ2分布、F分布、二项分布和Poisson分布的极限分布。故当涉及前述5种分布的概率密度函数（对连续型随机变量而言）或概率函数（对离散型随机变量而言）或分布函数的计算时，若直接计算的工作量很大，可考虑利用正态分布进行近似计算。因篇幅所限，具体计算方法从略。

4 讨论与小结

4.1 讨论

正态分布不仅是Z检验的理论依据，也是t检验和方差分析的前提条件之一，还是线性统计模型的建模依据（例如，要求模型的随机误差服从正态分布，通常是直接转变为考察定量因变量是否服从正态分布，若不符合正态性要求，可采取Box-Cox变换）［6］，甚至可以说，正态分布是经典统计学的根基（例如，进行很多参数假设检验和区间估计时都要求各组定量资料满足正态性、进行Pearson相关分析时要求两个定量变量满足双变量正态分布等，且许多其他概率分布的极限分布都是正态分布）。由此可知，无论是学习还是运用统计学，正态分布都是不可忽视的重要知识点或统计基础。

4.2 小结

本文介绍了“与Z检验有关的基本概念”“正态分布与其他概率分布之间的关系”和“正态分布可用于某些其他概率分布的近似计算”三部分内容。第一部分详细地介绍了“Z检验的适用场合”，为研究者合理选用Z检验奠定必要的基础。