管井承压水降水的流固耦合分析

魏芸，袁琳

（中交第一航务工程勘察设计院有限公司，天津 300222）

0 引言

承压水降水容易引起地表沉降，对大多数的深基坑工程而言都是一个不可回避的问题，特别是当基坑周边有建筑物存在时，准确预估承压水降水对建筑物的影响就显得尤为重要。承压水降水的沉降准确预估一直以来是工程中的一个难点，近年来许多学者及工程界人士从理论及应用层面都展开了研究[1-9]。但工程中涉及到管井降水时，首先需要遵循现行相关规范。因此本文用规范算法确定承压水降水水头和管井布置方案，之后利用有限元流固耦合分析方法对承压水降水过程进行了模拟，只需要简单的输入条件就可以得到承压水的降水过程线。

1 依托工程概况

某码头翻车机房及廊道工程主体采用钢筋混凝土结构。翻车机房主体长约64.2 m，宽约61.7 m，深约20 m，底板顶面结构标高-12.8 m，漏斗层顶标高-1.0 m，顶板顶标高-5.314 m，机房中部沿横向设有20 mm宽变形缝。翻车机房基坑支护结构为圆形地下连续墙，内径77 m，外径80 m，墙厚1.5 m。坑底标高-15.4 m。

2 地质条件、水文地质条件及周边环境

典型钻孔各土层主要物理、力学性质指标如表1所示。

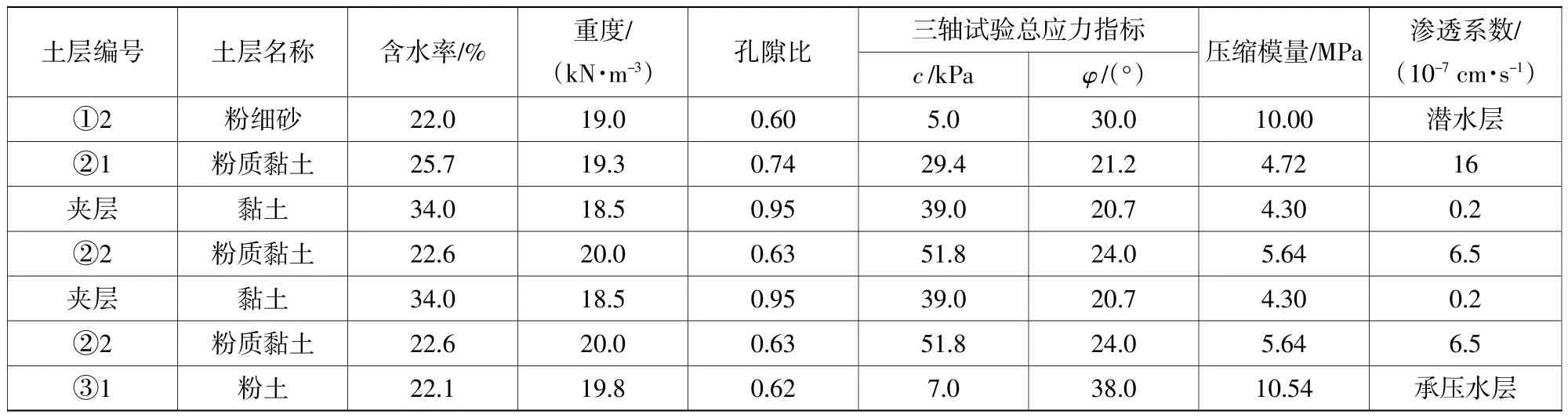
表1 典型钻孔各土层指标Table 1 Soil parameters from typical boreholes

勘查报告显示承压水主要赋存于下部③1粉土中，承压含水层顶板高程为-28.33～-34.00 m，顶板埋深为34.20～39.50 m。从钻孔资料看，其含水层厚度较大，为7.80～10.90 m。从区域地质资料看，地下水侧向径流与越流为场区承压水的主要补给与排泄方式。依据抽水试验报告，承压水含水层的渗透系数为3.34 m/d，影响半径为35.6 m，水位标高3.13 m。

本工程基坑西侧边缘外17 m分布1条铁路，基坑东侧边缘外分布1栋6层框架结构的职工宿舍楼，基础采用高强预应力空心管桩，桩长14 m，距基坑边缘39.2 m。

3 承压水降水设计（规范算法）

首先需要评估承压水降水的必要性，即需要进行基坑底面的突涌稳定性验算。依据JGJ 120—2012《建筑基坑支护技术规程》第C.0.1条：

式中：Kh为突涌稳定安全系数，不应小于1.1；D为承压水含水层顶面至坑底的土层厚度；γ为承压含水层顶面至坑底土层的天然重度；γw为水的重度；hw为承压含水层顶面的压力水头高度。

按典型钻孔计算得到：

Kh=Dγ/hwγw=0.78＜1.1

不满足规范要求，需采取措施保证施工安全，下面是承压水降水设计。

1）坑内水位降深确定

按式（1）可求得满足抗突涌稳定时，坑内承压水位降深标高约为-6.1 m。

2）基坑降水总涌水量计算

依据JGJ 120—2012《建筑基坑支护技术规程》第E.0.3条，群井按大井简化时，降水总涌水量可按式（2）计算：

式中：Q为基坑降水总涌水量，m3/d；k为渗透系数，m/d；M为承压含水层厚度，m；sd为基坑地下水位的设计降深，m；R为降水影响半径，m，取35.6 m；r0为基坑等效半径，m，可按r0=计算，A为基坑面积，m2。

算得Q=3 966 m3/d。

3）单井出水能力计算

管井的单井出水能力依据JGJ 120—2012《建筑基坑支护技术规程》式（7.3.16）计算：

式中：q0为单井出水能力，m3/d；γs为过滤器半径，m；l为过滤器进水部分的长度，m。

算得q0=949.5 m3/d

4）按出水能力确定井数

由JGJ 120—2012《建筑基坑支护技术规程》式（7.3.15）可得降水井数量n最少应为：

5）按式（4）计算出的井数计算承压完整井的地下水位降深

由JGJ 120—2012《建筑基坑支护技术规程》第7.3.10条，承压完整井的地下水位降深可按式（5）计算：

式中：si为基坑内任一点的地下水位埋深，基坑内各点中最小的地下水位降深可取各个相邻降水井连线上地下水位降深的最小值，当各降水井的间距和降深相同时，可取任一相邻降水井连线中点的地下水位降深，m；sw为井水位降深，m。

代入算得sw=87 m，即当只布5口井时，要想使基坑底部降水标高达到-6.1 m，需要每口井的水位降深达到87 m，该值远大于管井长度，显然不合理。因此，需要增加管井数量。这个过程只能通过试算完成。假定管井数为12口，同样可求得管井处水位降深为24 m，相应的水位标高为-20.87 m。

自此，降水井的数量及降水井处的水位降深完全确定，即需布置12口井，每口井的水位标高应保持在-20.87 m标高处。

4 承压水降水流固耦合分析

由于本工程承压水会导致基坑底部突涌破坏，承压水初始总水头+3.13 m，降水井处降水标高为-20.87 m。数值模型如图1所示。

图1 数值模型Fig.1 Numerical model

由于A区域有建筑物基础，B区域有铁路穿行，均是沉降重点关注区域。本次计算采用完全应力-渗流耦合，即抽水引起的渗流场变化会直接影响应力场计算，反过来应力场计算结果又会影响渗流场，如此往复直到数值解达到收敛标准。通过计算可得到渗流场随时间的变化以及整个应力场中位移随时间的变化。

本次计算只考虑承压水，因此，初始地应力平衡应得到只有承压含水层的孔隙水压力分布，该含水层顶板标高-28.33 m，底板标高-40.68 m，承压水水头3.13 m，则承压水层孔压为314.6～438.1 kPa。软件计算得到承压含水层降水前的孔压为310～430 kPa，其它土层孔压为零。由于数值结果是基于单元平均值给出的结果，可以说计算结果与预期十分相符，说明数值模拟的边界条件设置正确。

降水阶段计算，主要提取降水不同时间的孔隙水压力场和位移场云图如图2所示。

图2 孔压场随时间变化图Fig.2 Real-time variation contour of porepressure field

由图3可见，虽然降水井处的水位降深标高是-20.87 m，但是由于降水井直径较小，土层内的承压水压力是随着时间逐渐减小的，降水后1 d、2 d、5 d、11 d基坑中部的孔隙水压力分别是-125 kPa、-104 kPa、-91.5 kPa、-80.8 kPa（限于篇幅只给出历时1 d和11 d的孔压分布），对应的水位降深标高分别是-15.83 m、-17.93 m、-19.18 m、-20.25 m，可见在降水后11 d左右基坑中心达到的降深基本与降水井内一致。

图3 基坑中心线剖面位置孔压分布Fig.3 Pore pressure distribution at thesection of the center lineof the foundation pit

同时，从计算结果中提取铁路沿线离基坑最近的18 m位置点处的沉降值约为18 cm，外委楼桩基础离基坑最近的40 m位置点处的沉降约为11 cm，与现场实测值相近。

5 结语

本次分析采用完全应力-渗流耦合，计算过程只需要输入降水井设计降深，其它均由边界控制，人为因素干扰少，计算结果能够提取不同时间孔压及沉降的变化，能够客观地模拟承压水降水。值得注意的是，承压水的补给条件极大地影响计算结果，目前只能通过增大计算模型的边界减弱或消除这种影响，降水层渗透系数越大，需要的模型就越大。