基于超声振动的土壤切削挖掘装置设计与试验

王东伟 王家胜

(青岛农业大学机电工程学院， 青岛 266109)

0 引言

土壤耕作、深松以及根茎类作物挖掘收获等作业是农业生产中阻力最大、耗能最高的环节。节能降阻一直是该领域的研究重点，其中振动方式是一种降低土壤作业部件工作阻力的有效途径。所施加的振动频率通常为小于30 Hz的低频振动，文献[1-4]研究表明，通过外部动力按照一定振幅和频率驱动触土部件振动，其工作阻力能够得到有效降低，但总耗能一般要比非振动状态下高[5]。振动能量的传递会使连接部件甚至整机产生振动、冲击和噪声，并导致机器寿命下降。超声波振动频率超过20 kHz，超声高频振动辅助切削技术在金属加工领域，特别是硬脆合金材料的车、钻、磨等方面的应用研究较多，相比传统切削，超声振动辅助切削的工作阻力显著降低，而且切削面质量更高[6-8]。在食品加工领域，超声振动技术被应用于干酪等食品切割上，表现出摩擦力小、切面光滑干净、表面损伤小等优点[9-12]。近年来，超声振动技术逐渐应用于更多材料的辅助切削上，并表现了突出的优越性。文献[13-14]设计了Nomex蜂窝材料和气凝胶材料超声辅助切割装置，试验表明，切削阻力大幅降低；文献[15]对柳枝稷和芒草茎秆超声振动辅助切割进行了研究，切削能量最大可节省80%；文献[16]对云杉和山毛榉两种木材的超声辅助切割试验表明，其工作阻力比传统切割降低50%。

本文提出基于超声振动的土壤切削挖掘装置结构方案，以耦合谐振为目标，设计并集成超声换能器、变幅杆、铲刀等关键部件结构参数，搭建超声振动土壤切削挖掘阻力试验测试平台，通过阻力对比试验验证该装置的降阻特性，为研发超声振动土壤作业机具提供理论依据和参考。

1 结构方案与振动降阻理论分析

1.1 结构方案

图1为实现超声波高频振动土壤切削挖掘装置的结构示意图。该装置主要由超声波发生器、换能器、变幅杆、法兰盘以及土壤切挖部件等组成。工作过程中，首先由超声波发生器产生高频振动电信号，再经换能器将超声电信号转变为高频机械振动波，变幅杆两端分别连接换能器输出端和土壤切挖部件的柄端，其作用是将超声机械波进一步放大后传递给触土部件，激励触土铲刀的高频纵向振动，以降低土壤切削挖掘阻力。法兰盘设置在变幅杆上零位移节点位置，与外驱动部件连接，带动超声振动土壤切削装置前进作业。

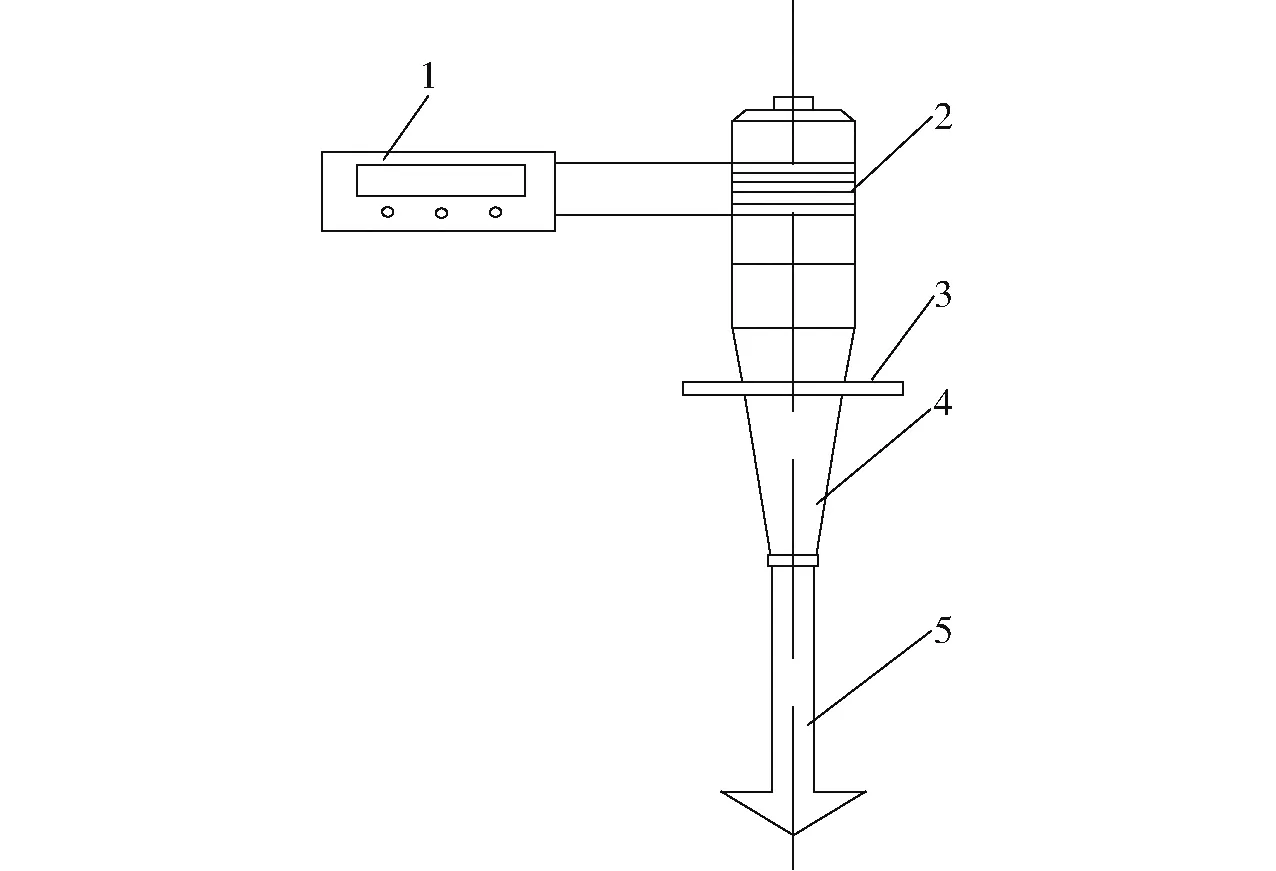
图1 超声振动土壤切削挖掘装置结构示意图Fig.1 Structural sketch of ultrasonic vibration soil cutting and digging device1.超声波发生器 2.换能器 3.法兰盘 4.变幅杆 5.土壤切挖部件

1.2 振动降阻理论分析

图2为超声振动土壤切削原理图。振动方向沿铲刀的纵向方向，则铲尖在水平方向的位移为触土部件的振动位移与前进位移之和，即

xr=vt+Asin(ωt)cosθ

(1)

式中xr——铲尖在水平方向的综合位移，m

v——触土部件前进速度，m/s

t——时间，sθ——入土角，(°)

A——振幅，mm

ω——振动角频率，rad/s

图2 超声振动土壤切削原理图Fig.2 Schematic of ultrasonic vibration soil cutting

对式(1)求导可得铲尖在水平方向上的合速度为

vr=v+Aωcos(ωt)cosθ

(2)

式中vr——铲尖在水平方向上的合速度，m/s

式(2)中动态速度项Aωcos(ωt)cosθ取值区间为(-Aωcosθ,Aωcosθ)，如果-Aωcosθ<-v，则vr<0，此时铲的触土面与前端硬土处于分离状态，前进方向上没有互作力。入土角θ确定，振幅与振动频率的乘积Aω将决定作业过程中是否满足铲面与土壤分离的条件以及铲、土分离时间。超声波的高振动频率会有利于增加土壤挖掘过程中铲面与土壤的分离机会，但由超声波发生器与换能器产生的超声机械波振幅较小，通常只有4～10 μm，还需要设计参数匹配的变幅杆，实现装置的耦合谐振，利用其聚能作用将进一步放大振幅，从而增大振动速度，达到降低阻力的目的。

2 关键部件及参数设计

2.1 超声频率确定

为实现装置的耦合谐振，超声激振频率是决定换能器和变幅杆结构和尺寸的基础参数。特定频率超声波信号由他激式振荡电路超声波发生器产生，当前工业中常用的超声波频段基本在20～100 kHz之间，但频率越高，与之配套的换能器产生的热量越大，不利于长时间工作，因此该方案选定20 kHz作为超声振动频率，换能器、变幅杆及铲刀结构将基于该频率进行设计。

2.2 换能器参数设计

2.2.1夹心式换能器结构

超声波换能器是利用逆压电效应原理将超声波发生器传递的电能转换为机械能。夹心式压电陶瓷换能器结构如图3所示。

图3 夹心式压电陶瓷换能器结构图Fig.3 Structure of sandwich piezoelectric ceramic transducer1.预应力螺栓 2.后盖板 3.压电陶瓷片 4.前盖板

换能器采用偶数片环形压电陶瓷片串联，陶瓷片间装有金属电极，再由前、后盖板经预应力螺栓将其连接为一体，超声波发生器产生的高频电信号接入施加于金属电极片所形成的高频电场与压电陶瓷片作用后，转换为高频机械振动并传递出去即为超声波。

2.2.2压电陶瓷片参数

该系统选用4片环形PZT-8型压电陶瓷片，每片厚度5 mm。为了避免换能器谐振频率与压电陶瓷径向振动相耦合而导致纵向振动效率降低，压电陶瓷片直径应不大于对应频率超声波在陶瓷中1/4波长[17]，即

(3)

式中D——陶瓷片外径，mm

ce——压电陶瓷等效声速，m/s

f——谐振频率，Hz

根据压电陶瓷杨氏模量和密度可查得ce=3 183 m/s，取f=20 kHz，代入式(3)得D≤40.5 mm，取D=40 mm。

2.2.3前、后盖板参数

换能器前盖板主要功能是将产生的超声振动能量高效纵向辐射出去，选用机械损耗小的高强度硬铝材料2A12加工而成。为了实现换能器单向无障碍辐射，后盖板材料选用符合该要求的45号钢。前、后盖板均采用等截面圆柱状，截面直径与陶瓷片外径相等，均为40 mm。为实现系统谐振，前后盖板长度可利用频率方程计算确定[18]

(4)

(5)

式中ρ——压电陶瓷密度，kg/m3

ρ1、ρ2——前、后盖板材料密度，kg/m3

l1、l2——前、后盖板长度，mm

c1、c2——前、后盖板声速，m/s

lc1、lc2——位移节面两侧1/4波长振子中陶瓷片长度，mm

S1、S2——前、后盖板截面积，mm2

S0——压电陶瓷片截面积，mm2

由f=20 kHz，可得ω=1.256×105rad/s；根据前、后盖板材料可知其密度分别为ρ1=2 700 kg/m3，ρ2=7 800 kg/m3，对应的声速为c1=5 092 m/s，c2=5 189 m/s；根据压电陶瓷片的厚度可知lc1=5 mm，lc2=15 mm；因压电陶瓷片与前、后盖板截面积均相等，由D=40 mm，可得S0=S1=S2=1.96×10-3m2；将以上参数代入式(4)、(5)可求得前、后盖板长度分别为l1=58 mm，l2=30 mm。

2.3 变幅杆参数设计

2.3.1变幅杆振动理论模型

变幅杆的聚能作用体现在将微小振幅超声振动进一步放大并传递给负载部件。在忽略传播损耗的前提下，相同时间通过变幅杆截面的能量是不变的，所以变幅杆是通过减小截面积来增大能量密度。能量密度与振幅的关系为[19]

ρE=ρhchω2A2

(6)

ρh——变幅杆密度，kg/m3

ch——变幅杆传播声速，m/s

即能量密度与振幅的平方成正比，因此，超声波振幅也是随变幅杆的截面积减小而增大。为了获得较大振幅，应使变幅杆的固有频率接近或等于激振频率，使之处于共振状态。变幅杆固有频率由其材料、质量及结构尺寸决定。

在超声简谐振动下，变幅杆纵向振动方程为[20]

(7)

式中ξ——变幅杆质点振动位移函数

S——沿变幅杆纵向坐标截面积函数

x——变幅杆轴向坐标，mm

kh——变幅杆声波数，mm-1

Let Eqs. (6) – (5), finally we get the output resistance:

目前常用的变幅杆结构类型可分为圆锥型、阶梯型、指数型等。针对土壤切削的特点，选抗弯强度好、稳定性高且易加工的圆锥形变幅杆。变幅杆选材应满足传递超声振动能量损耗小、疲劳强度高、声阻抗小及易加工等要求。钛合金可很好地满足以上要求，但价格太高，综合考虑，选用45号钢作为变幅杆材料。

圆锥形变幅杆如图4所示，振动由连接换能器的大头传向连接触土部件的小头，根据锥体几何关系，得其截面积及截面直径分别为

Sh=Sb(1-αx)2

(8)

Dh=D1(1-αx)

(9)

其中

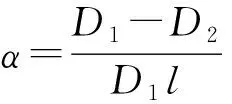
式中Dh——变幅杆截面直径，mm

Sh——变幅杆截面积，mm2

Sb——变幅杆大头截面积，mm2

D1——变幅杆大头截面直径，mm

D2——变幅杆小头截面直径，mm

α——比例系数，mm-1

l——变幅杆长度，mm

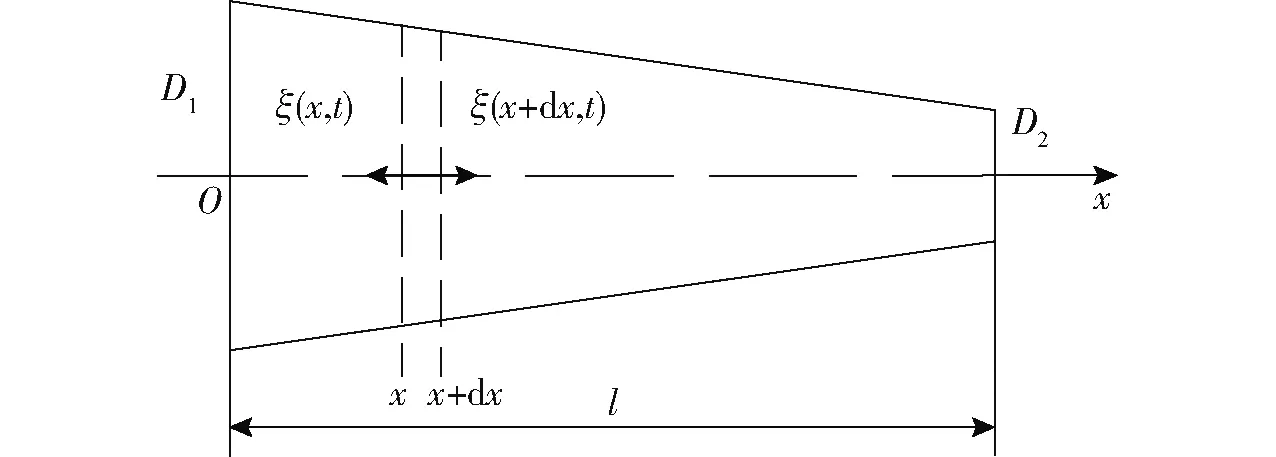
图4 圆锥形变幅杆振动示意图Fig.4 Vibration diagram of conical horn

由圆锥形变幅杆截面积函数式(8)、(9)，求得满足式(7)的解为

(10)

式中A1、B1——常数项

则变幅杆质点应变为

(11)

2.3.2变幅杆谐振长度设计

(12)

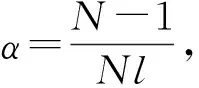
(13)

将已知条件数据代入式(13)，通过数值计算可得到不同变幅杆大、小头直径比与谐振长度的关系曲线如图5所示。由图5可以看出，随变幅杆两端直径比的增大，变幅杆谐振长度呈非线性增大。

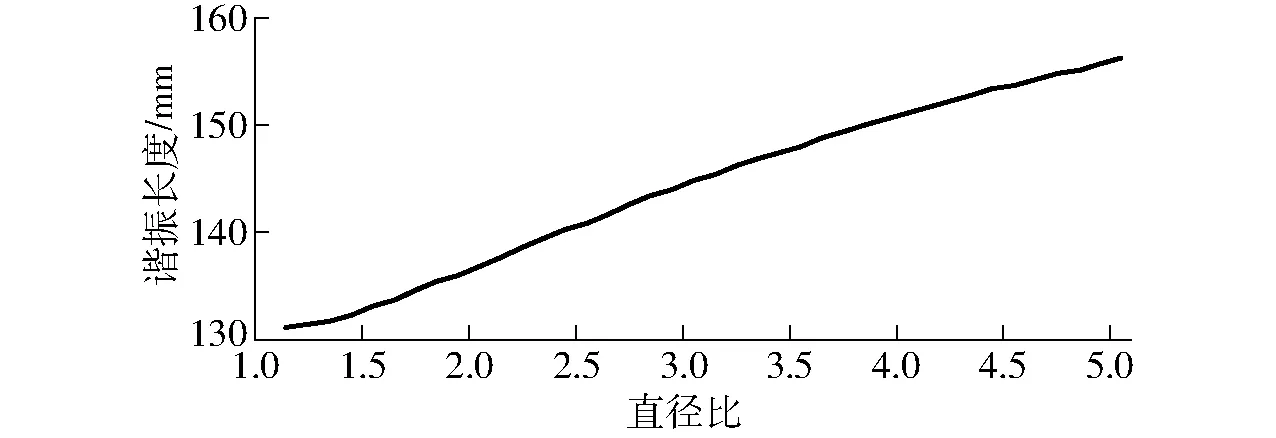
图5 变幅杆直径比与谐振长度的关系曲线Fig.5 Relation curve between diameter ratio of horn and resonance length

变幅杆大头直径与换能器前盖板直径相同，即D1=40 mm，取小头直径D2=20 mm，则N=2，则由式(13)计算得变幅杆谐振长度l=137 mm。

2.3.3位移节点确定

变幅杆位移节点是指振幅为0的点。该点所在的截面是对变幅杆也是对整个部件的夹持固定位

置，有效避免振动能量的外泄。

(14)

式中ξ1——变幅杆输入端最大振幅，mm

基于式(14)，由位移节点条件：x=x0，ξ=0，可得

(15)

式中x0——变幅杆位移节点坐标， mm

将kh=24 mm-1，α=3.65 mm-1代入式(15)，求解得x0=54 mm。

3 超声变幅杆模态分析与谐响应分析

3.1 变幅杆有限元模型

变幅杆谐振的条件取决于变幅杆的材料及结构尺寸，为检查和验证理论设计的正确性，基于有限元仿真软件ANSYS Workbench对锥形变幅杆进行模态分析和谐响应分析。

利用SolidWorks按照设计尺寸对变幅杆几何建模后导入有限元软件ANSYS Workbench，材料取45号钢。根据位移节点位置的理论计算值，在距变幅杆大端面54 mm处固定一法兰圆盘作为切削装置与外部驱动机构的连接点，此处纵向振幅为0，法兰盘面即为动力仿真的固定约束面。网格单元类型采用20个节点的六面体单元(solid186)。有限元模型如图6所示。

图6 锥形变幅杆有限元模型Fig.6 Finite element model of conical horn

3.2 模态分析

模态分析的拓展阶数为11阶，最大振动频率可达23.016 kHz，根据分析结果发现，前11阶振动模态振动方向包括弯曲、扭转、伸缩等不同类型，其中第8、9、10、11阶模态分析图如图7所示。根据仿真结果，第9阶和第10阶模态为与超声激振方向一致的轴向伸缩振动，振动频率分别为16.267、20.096 kHz。2个模态的输入与响应相位差分别为0°和180°，即第9阶模态下，变幅杆大端面振动与小端面振动方向同步，而第10阶模态下，变幅杆大端面振动与小端面振动方向相反。第10阶模态振动频率与设计频率的误差小于1%，与理论值吻合较好，满足变幅杆的设计要求。

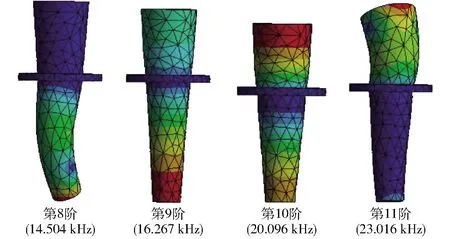
图7 第8、9、10、11阶模态分析图Fig.7 8th～11th order modal analysis diagrams

3.3 谐响应分析

谐响应分析搜寻频率设置为19～21 kHz，轴向激振力施加在变幅杆大端面，从变幅杆小端面测量响应振幅，响应曲线如图8所示。

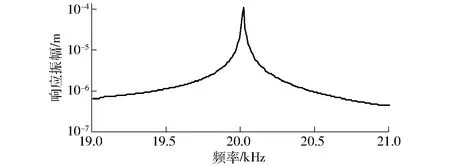
图8 圆锥形变幅杆谐响应曲线Fig.8 Harmonic response curve of conical horn

由图8可知，变幅杆输出端响应振幅在频率为20 kHz附近达到最大值，因此，超声变幅杆能够较好地实现在频率为20 kHz超声下谐振，对振动能量高效传递。仿真结果验证了超声变幅杆理论设计参数的正确性。

4 试验验证

4.1 试验系统构建

超声振动土壤切削挖掘阻力试验测试系统如图9所示。该系统主要包括超声振动切削装置、土槽、伺服电机、力学传感器、数据采集卡、计算机以及软件测控程序等。

图9 超声振动土壤切削挖掘阻力试验测试系统原理图Fig.9 Test system for soil cutting resistance with ultrasonic vibration1.伺服电机 2.力学传感器 3.数据采集卡 4.计算机 5.运动导轨 6.超声振动切削装置 7.土槽

将超声振动土壤切削挖掘装置安装在试验台的运动导轨上，切削装置可在伺服电机驱动下沿导轨直线往复运动。试验台底部安置土槽，则切削装置在前进过程中实现对土槽内土壤的切削挖掘。传感器将所测得数据经数据采集卡传入计算机测控程序，测控程序除了能够采集、显示和存储试验数据外，还可对试验台伺服驱动装置进行控制，实现切削装置运动状态的实时控制及运动与电流参数的采集等功能。按照设计方案试制的试验台如图10所示。

图10 超声振动土壤切削挖掘试验台装置Fig.10 Test bed for soil cutting with ultrasonic vibration

4.2 试验方法

在相同土壤条件下进行有、无超声振动的土壤切削挖掘阻力和耗能对比试验。阻力可直接由测定数据统计得到。耗能对比试验中，土壤挖掘耗能计算式为

EⅠ=Rvt

(16)

式中EⅠ——克服切削挖掘阻力耗能，J

R——切削挖掘阻力，N

振动土壤挖掘耗能除了克服切削挖掘阻力耗能外，还包括振动激励耗能，可利用超声波发生器所耗电能来代替，其计算式为

EⅡ=UIt

(17)

式中EⅡ——振动激励耗能，J

U——工作电压，V

I——工作期间平均电流，A

则振动土壤挖掘总耗能为克服阻力耗能与振动激励耗能之和。与无振动耗能对比可用耗能比来表示，计算式为

(18)

式中e——耗能比

Ev——超声振动下切削挖掘总耗能，J

Eo——无振动切削挖掘耗能，J

试验用土壤类型为壤土，土壤硬度分别设为1.5、2.5、3.5 MPa，土壤含水率在20%～48%间取值，挖掘铲入土角为20°、挖掘深度为8 cm。加载速度为3 000 mm/min。试验前对土槽内土壤进行整备，整备工艺为翻松碎土-整平-洒水-压实4道工序，整备后的土壤满足预设的土壤硬度和湿度要求；在相同土壤条件和工作参数下通过开、闭超声波发生器分别进行有、无超声振动土壤切削挖掘阻力和耗能对比试验，采集并记录试验数据，每组试验重复3次。

4.3 试验结果与分析

图11显示了在土壤硬度为2.5 MPa、土壤含水率为26%时，有、无超声振动土壤切削挖掘阻力时间历程曲线。2条曲线对比显示，加载超声振动下，土壤切削挖掘阻力明显降低。对重复试验数据进行统计计算得无超声振动土壤平均切削挖掘阻力为142 N，超声振动土壤平均切削挖掘阻力为84 N，降阻率达40.7%。

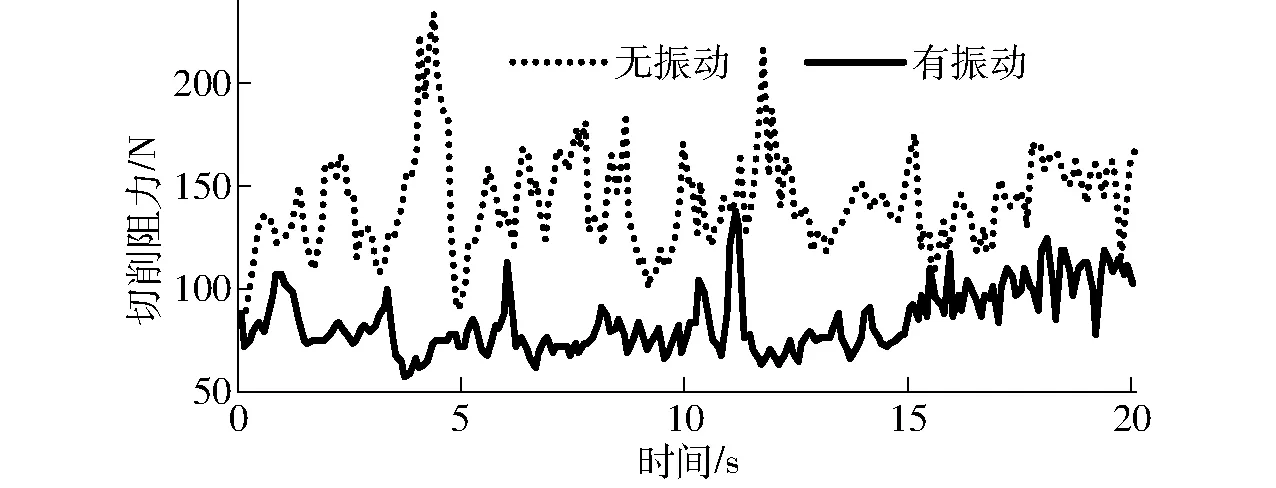
图11 土壤切削挖掘阻力时间历程曲线Fig.11 Curves of soil cutting resistance with time

图12是在土壤湿度26%时，3种不同土壤硬度对应超声波振动挖掘铲和无振动刚性铲土壤切削挖掘阻力的对比。在土壤硬度为1.5 MPa时，超声波振动铲降阻率为35.1%，而当土壤硬度增大到2.5 MPa和3.5 MPa时，对应的降阻率也分别增加到40.7%和44.3%。由此可见，土壤硬度越大，超声波振动挖掘铲的降阻效果越好。

图12 3种土壤硬度下有无振动土壤切削挖掘阻力比较Fig.12 Comparison of soil cutting resistance with and without vibration under three soil hardness

图13显示了土壤含水率从20%到48%区间，有、无振动土壤切削挖掘阻力的变化曲线。由图中可以看出，不论有无振动，土壤切削挖掘阻力都随着土壤含水率的增加先迅速降低，然后又缓慢回升。对比2条变化曲线发现，除了高频振动作用下的阻力明显降低外，还可看出在低含水率(20%)和高含水率(48%)的曲线两端，其阻力的降低幅度稍大于中间段。

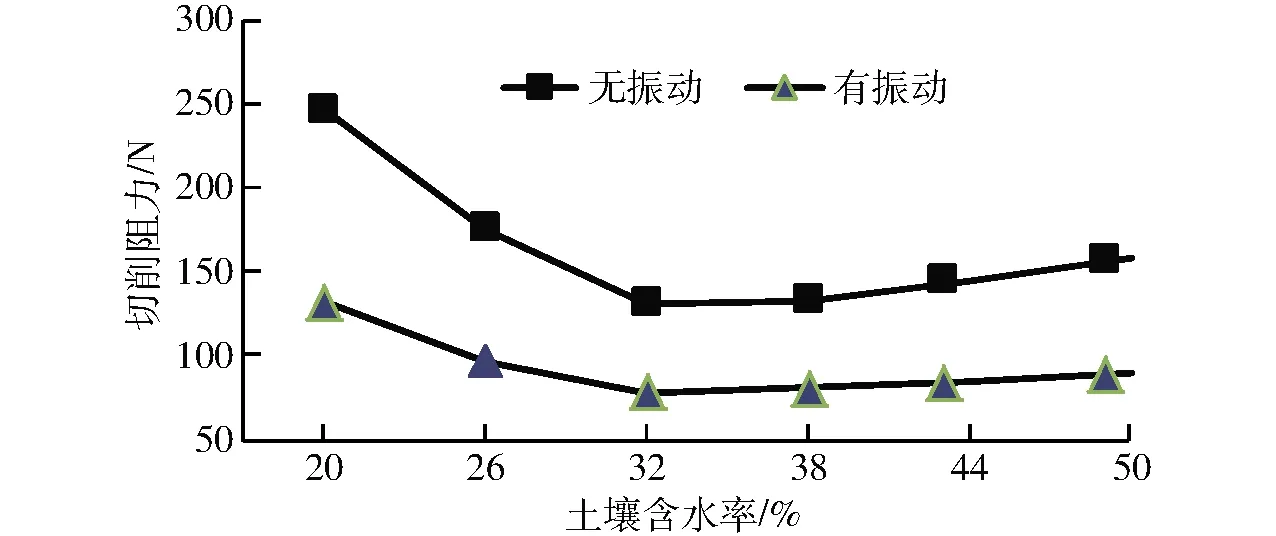
图13 不同土壤含水率下土壤切削挖掘阻力曲线Fig.13 Soil cutting resistance curves under different soil moistures

由于超声振动激励下工作阻力有效降低，触土部件克服阻力耗能也会得到有效降低。但激励触土部件振动需要超声波发生器消耗额外能量。根据试验统计，超声波发生器工作电压为220 V，在土壤硬度分别为1.5、2.5、3.5 MPa下对应平均工作电流分别为8、12、26 mA，可见土壤硬度越大，振动耗能越大。如考虑其综合耗能，分别利用式(16)～(18)统计计算出土壤硬度为1.5、2.5、3.5 MPa下所对应的有无振动土壤挖掘耗能比为0.98、0.93和1.04。计算结果表明，在某些土壤硬度条件下振动挖掘耗能得到了一定降低，但降低效果不明显，某些状态还略高于无振动挖掘耗能。尽管如此，由于超声振动辅助土壤挖掘能够显著降低工作阻力，这就降低了触土部件对动力驱动装备的功率要求；同时，低功率动力装备因自身质量减轻还会减小对农田土壤的压实影响。

试验结果表明，在不同典型土壤硬度和土壤含水率条件下，影响降阻特性的激振频率、换能器与变幅杆关键结构参数能够实现有效匹配和装置的耦合谐振，土壤切削挖掘阻力均能得到有效降低，从而验证了超声波振动挖掘装置设计方案的可行性和设计参数的正确性。

5 结论

(1)设计了超声振动土壤切削挖掘装置。选定20 kHz作为超声激振频率，基于耦合谐振效应的目标，分析、设计了夹心式换能器和圆锥形变幅杆等关键部件的结构参数。建立了变幅杆有限元模型，利用仿真方法对其进行模态分析，仿真结果显示，变幅杆轴线伸缩固有频率接近20 kHz，与设计值吻合。

(2)搭建了超声振动土壤切削挖掘阻力试验测试平台，进行了有、无超声波振动土壤切削挖掘阻力土槽对比试验。结果表明：相比无振动刚性挖掘铲，超声波振动挖掘铲能够有效降低土壤切削挖掘阻力，在1.5、2.5、3.5 MPa 3种土壤硬度条件下，超声波振动挖掘铲所对应的降阻率分别为35.1%、40.7%和44.3%，土壤硬度越大，超声波振动挖掘铲的降阻效果越明显。不论有无振动，土壤切削挖掘阻力均随着土壤含水率的增加先迅速降低后又缓慢回升。由于超声振动激励需额外消耗能量，故振动挖掘总耗能并未降低。