模式转换下养老金投资与提前支取的博弈问题研究

郝雪妍，闫 明

(1.贵州民族大学 数据科学与信息工程学院，贵州 贵阳 550025；2.天津财经大学 管理工程与科学学院，天津 300222)

养老金计划从1889年德国开始执行至今，已成为全球普遍接受的社会保障措施。我国从1997年起实行社会统筹和个人账户相结合的养老保险制度，目前养老基金规模日益扩大。社会养老基金管理是影响数代人的实际利益与社会福利的重大策略。为了提高基金的使用效率并兼顾代际公平，需要管理和科研人员寻求更为细致且可动态调整的方法管理与分配相关资产。本文关注其中一个重要课题：如何在基金过剩时平衡当前与未来参与者的利益。

根据支付和缴费方式的不同，养老金计划可以分为固定缴费模式和固定收益模式。固定缴费(defined contribution, DC)模式确定缴费水平或缴费比率，收益水平与账户积累额直接关联。固定收益(defined benefit, DB)模式事先明确未来的收益水平,缴费水平根据未来收益通过精算均衡原则进行计算核定。近年来，有关DB型养老金投资的研究受到了许多研究者的关注。比如Josa-Fombellida和Rincón-Zapatero[1]研究了具有随机利率的总固定收益养老基金的最优资产配置，Hainaut和Deelstra[2]研究了固定收益养老金计划的最优资金，Josa-Fombellida和Rincon-Zapatero[3]研究了在确定收益随机养老基金的最优风险管理，他们考虑了收益或风险资产的发展变化。Merton[4]考虑了在连续时间模型中的最优消费和投资组合。王愫新和荣喜民[5]研究了保险公司向再保险公司购买比例的保险，得到最优投资策略和再保险策略。李仲飞和陈峥[6]研究了在不同时刻，消费者对消费的偏好由一个时变的风险厌恶系数刻画的最优投资—消费问题。

然而，由于投资的不确定性，根据精算均衡计算的DB型基金的实际资产与未来支出并不是时刻平衡的。当基金运营较好时，实际资产超过未来支出，出现超额(overfunded)。相反的，当经济下行，实际资产可能低于未来支出，出现缺额(underfunded)。在传统的框架下，DB基金的超额部分会继续投入资本市场，可能会提升基金未来的风险。事实上，近些年资本市场的波动和经济下行的风险增加，如2008年的次贷危机与2020年的新冠疫情均造成了全球养老基金的大幅缩水。在这种情况下，基金参与者通过某种机制提前取出部分超额资金作为未来风险的补偿，似乎是一种合理且受到普遍关注的需求。因此，合理处理该需求的有助于提高养老金计划的参与度，并且可实现社会福利更合理的代际分配。

Josa-Fombellida和Rincón-Zapatero 在2018年提出一类随机微分博弈模型处理对养老基金提前支取与投资增值的冲突。笔者认为，当DB型养老基金出现了超额，代表投资需求的投资公司以实现未来投资效益的最大化与代表提前支取需求的工会组织进行动态的非合作博弈。作者使用常数相对风险厌恶函数衡量双方效用，通过建模计算得到投资与提前支取的均衡策略的解析形式，并分析了风险厌恶系数对策略的影响。在经济分析中，作者讨论了在两种经济模式下的策略选择，即牛市与熊市。然而，这些经济模式并不是一成不变的，而是以一定的概率相互转换，这种转换来自于金融市场的不稳定性与结构性变化。目前，很多文献研究了相关的问题。如Hainaut和Donatien[7]考虑了在模式转化下的养老基金投入的冲动控制，Chen和Yam[8]，Jin和Yin 等[9]和Zhu[10]研究了在模式转换情形中保险公司的风险控制问题。

综上，本文在存在模式转换的市场中考虑养老金计划中投资与支取的策略选择问题。利用动态规划原理得到关于最优策略的Hamiton-Jacobi-Bellman方程组，利用数值方法计算此方程组得到相关策略。最后，我们使用韩国市场的数据分析了风险厌恶程度和模式转换强度对策略的影响。

1 博弈模型

1.1 金融市场与资金盈余过程

设(Ω,Ft,P)为完备概率空间，其中Ft是由Y(t)和W(t)产生自然域流过程，Y(t)是两值的连续时间马尔可夫链，其值为模式1和模式2，表示两种不同的市场状态，如牛市与熊市。模式i在单位时间内转换为模式j的强度为λi(j≠i)，即在无限小的时间段dt中[11-12]：

Probability(Y(t+dt)=j|Y(t)=i)=λidt.

设投资者有无风险资产(即债券)B和风险资产(即股票)S。假设B的利率r(t)为

r(t)=r(t,Y(t))

(1)

设b(t)和σ(t)分别表示风险资产S的回报率和波动率。我们令

b(t)=b(t,Y(t)),σ(t)=σ(t,Y(t)).

(2)

在状态i时，设r(t)=ri,b(t)=bi和σ(t)=σi，满足bi>ri和σi>0。设W(t)为标准布朗运动，则资产的动态过程为

dB(t)=r(t)B(t)dt,

(3)

dS(t)=b(t)S(t)dt+σ(t)S(t)dW(t).

(4)

假设投资公司(企业)是养老基金的投资决策者。X(t)表示在t时的资金盈余，初始资金X(0)>0。考虑博弈参与者之一：养老计划参与者，并以工会代表他们的整体。我们认为，养老计划的参与者是短视的，他们期望能在资金池中提前提取收益。在t时工会的博弈策略设为提取的收益P(t)。参与博弈的另一方为投资公司，它利用金融市场进行投资。本文中只考虑两类资本配置，即认为金融市场包括一种无风险资产和一种风险资产，而投资公司决策在这两类资产的投资份额。设它投资于有风险资产的金额设为π(t)，则它投资于无风险资产的金额设为X(t)-π(t)。根据投资公司的交易策略π(t)和工会的提取策略P(t)，得到基金池中的财富X(t)满足。

(5)

将(3)和(4)代入(5)得

dX(t)=(r(t)X(t)+π(t)(b(t)-r(t))-P(t))dt+σ(t)π(t)dW(t),

(6)

与初始条件X(0)=x>0共同构成资产盈余的动态过程。

设博弈双方的策略都是马尔可夫的，即在t时刻策略依赖于状态变量X(t)和状态变量Y(t)，也就是π(t)=π(X(t),Y(t))，P(t)=P(X(t),Y(t))，其中：

{π(X(t),Y(t)):t≥0}和{P(X(t),Y(t)):t≥0}是Ft-可测的。另外，我们设(P,π)满足可积性条件

给定X(0)=x和Y(0)=i，随机微分方程(6)存在唯一的解。将满足上述条件的策略集合记为AU和AF，分别表示工会和企业的可行策略集。为了表达简便，在不引起误解的情况下，下文中记(π(X(t),i),P(X(t),i))为(πi(t),Pi(t))，i∈{1,2}。

1.2 博弈参与者的收益函数

(7)

(8)

其中v是投资公司的效用函数，β>0是时间偏好。这里，使用常数相对风险厌恶(CRRA)效用函数:

可以证明，这些效用函数是严格凹的。

1.3 Nash均衡策略

在动态非合作环境中，相关的解是马尔可夫完全纳什均衡(MPNE)。养老金游戏的MPNE指的是一对可接受的策略(P*,π*)∈AU×AF，对于任何(P,π)∈AU×AF，

在文章中，对照组患者进行常规的护理，而观察组患者则实施优质护理，常规护理组的患者在病情及生活质量方面均有一定程度的改善，但相较于观察组的优质护理来说，差距较大，效果尚不理想[11-12]。饮食护理能够促使患者补充更多高蛋白食物，用药护理能够促进患者的病情改善，生活护理能够为患者提供舒适的治疗环境，改善患者的心境，进而促进病情改善[13-14]。在本文数据当中，观察组在依从性上和生活质量评分上，均较对照组有优势（P＜0.05）。

对于任何x>0和i∈{1,2}有

JU(x,i;P*,π*)≥JU(x,i;P,π*),

JF(x,i;P*,π*)≥JF(x,i;P*,π).

设VU,i(x)和VF,i(x)分别是i状态下工会和公司的价值函数，即

VU,i(x)=JU(x,i;P*,π*)，VF,i(x)=JF(x,i;P*,π*).

定义1：当i∈{1,2}时, 我们定义

函数hi(x)为hi(x)=λjx+(αs,iγ+λi)x1/γ-(αs,jγ+λj)-λix1/γ-1,

(9)

i,j∈{1,2},i≠j.

假设1：在本文中, 假设αs,i>0,βs,i>0,i=1,2.

引理1：在假设1条件下，任何i≠j∈{1,2}, 如果αs,i≥αs,j, 则方程hi(x)=0在(0,1]有唯一解ci，然而hj(x)=0在[1,∞)有唯一解cj. 否则，方程hi(x)=0在(1,∞)有唯一解ci，而方程hj(x)=0在(0,1)有唯一解cj. 在这两种情况下，ci=1/cj. 此外, 定义αi和βi为

命题1:在假设1条件下，工会和企业在纳什养老金博弈(6)，(7)和(8)中的价值函数为

(10)

(11)

均衡资金盈余是一个几何布朗运动过程,

dX*(t)=X*(t)[(r(t)+θ2(t)/δ-A-1/γ(t))dt+θ(t)/δdW]，

(13)

这里A(t)=Ai，Y(t)=i. 因此X*>0.

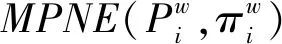
并满足值函数

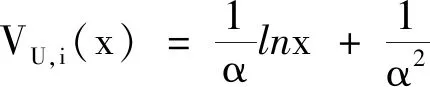
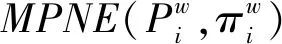
均衡资金盈余是一个几何布朗运动过程，

dX*(t)=X*(t)[(r(t)+θ2(t)-α)dt+θ(t)dW]，

因此X*>0.

2 经济分析

以Jang和Kim[13]的结果，采用1997年-2012年韩国综合股市相关参数进行研究。设μ1=μ2=0.684，σ1=0.2328，σ2=0.5003，r1=r2=0.0117，以及转换强度λ1=0.1063和λ2=0.7682. 对两个参与者取相同的折现因子等于0.98，这意味着α=β=0.02.此外，设δ=γ∈[1,10]，此时，

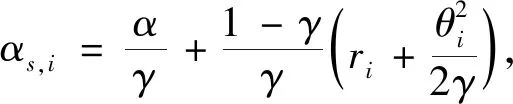
(14)

在该例中均为正。

图1表示在有和没有模式转换的两种制度下，工会在风险厌恶系数γ∈[1,10]下抽取的比例。如果不进行转换，在牛市中所得到的收益要比在熊市中高得多。因此，均衡策略要求工会在经济衰退时谨慎行事。在存在模式转化的情况下，在两个模式下提前抽取的收益占基金盈余的份额相似，且贴近牛市的策略。这是因为假设熊市以相对大的概率转化为牛市，而牛市则以较小概率进入熊市。这表示博弈参与者对市场现状存在较为乐观的预期，所以工会主张抽取更多收益，所抽取的基金盈余份额略低于市场一直保持牛市的情况。

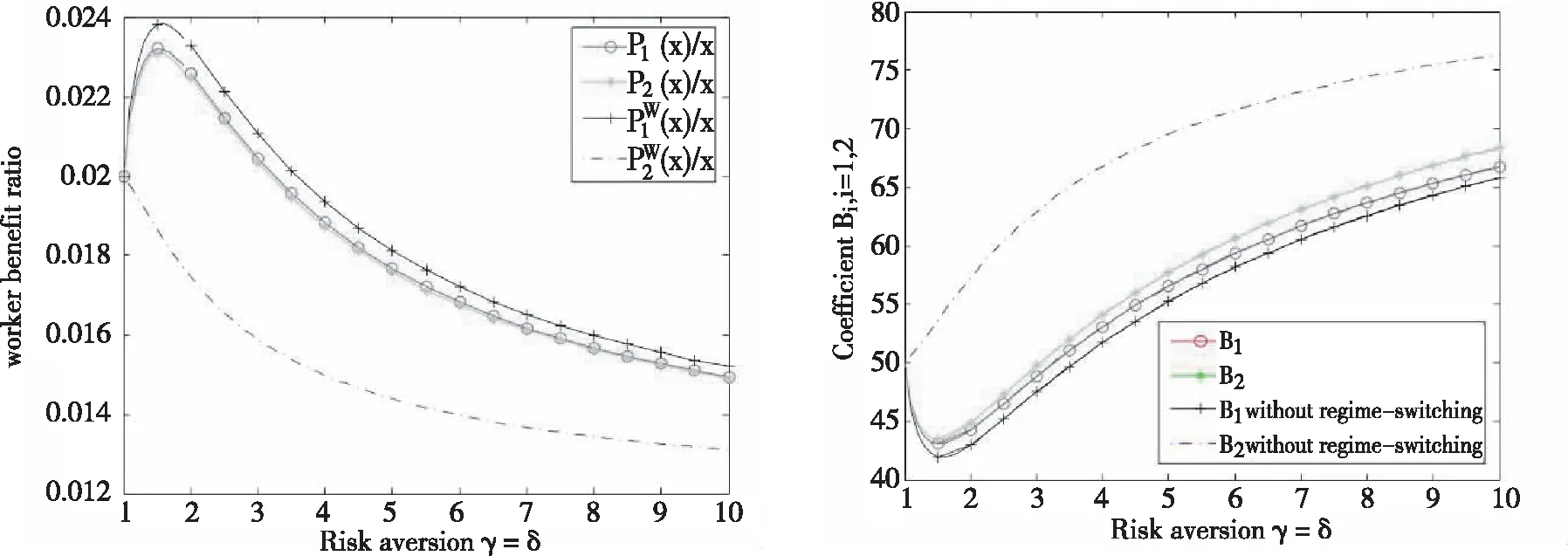
图1 不同风险厌恶系数下工会提前支取比率 图2 不同风险厌恶系数下公司值函数参数

图2表示在有和没有模式转换的两种情况下，投资公司在风险厌恶系数γ∈[1,10]下的值函数系数Bi的变化。如果不存在模式转换，那么熊市中的价格要比牛市中的价格高得多。可以解释这种行为，在蓬勃发展的经济中，工会要求比熊市获得更大的利益。因为δ>1，所以更小的Bi表示投资公司在相同的资金流时获得更大效用。在牛市中，投资公司由于对未来的乐观预期，所以其期望效用高于熊市的情况。在存在模式转换的情况下，投资公司的期望效用趋同且略低于没有模式转换牛市的情况。

图3显示在不同的模式转换强度下的工会的博弈策略。当研究牛市转换为熊市的转换强度λ1∈[0.1,1]的影响时，设置熊市转换牛市的转换强度为默认值λ2=0.7682。与此类似，研究熊市转换为牛市的转换强度λ2∈[0.1,1]的影响时，我们设置牛市转换熊市的转换强度为默认值λ1=0.1063。同时，我们设δ=γ=2。可以看出，随着λ1增大时，对市场的预期更加悲观，因此工会在两种模式下抽取更少的收益。相反的，随着λ2增加，对市场的预期更加乐观，工会在两种模式下抽取更多的收益。同时，我们看出在λi,i=1,2增加的情况下，两种模式下策略会有所靠近。

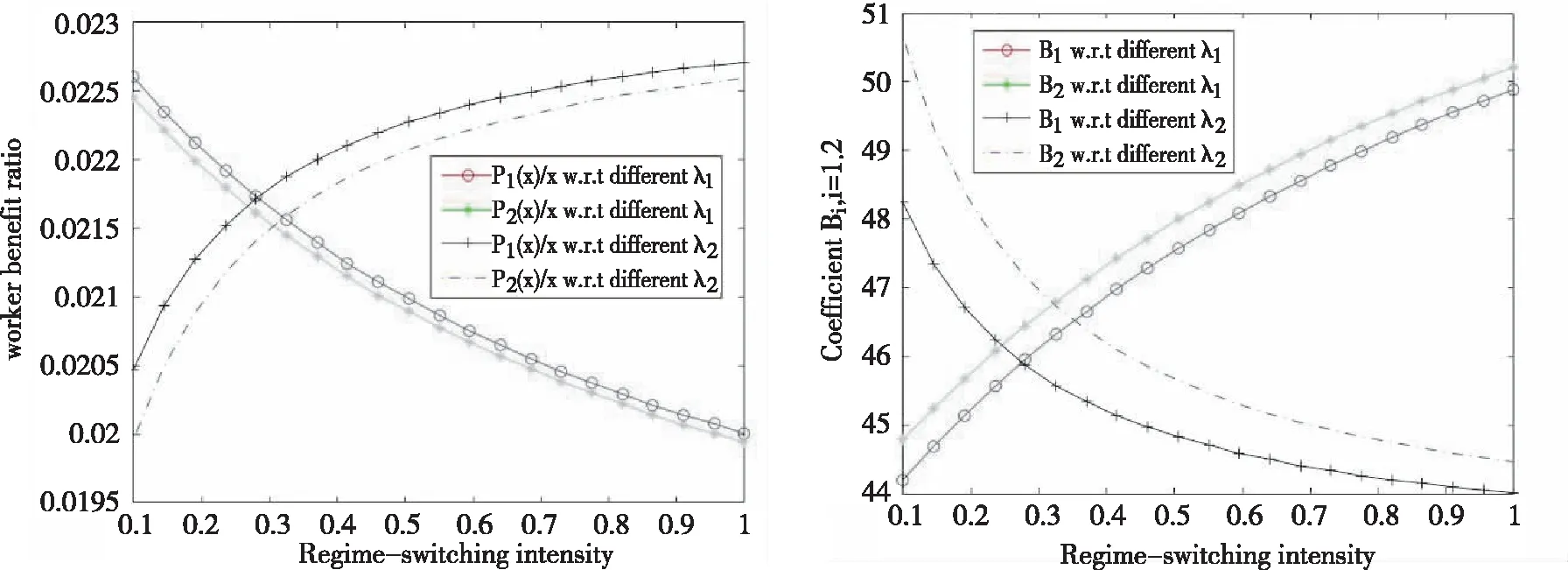
图3 不同模式转换强度下工会提前支取比率 图4 不同模式转换强度下公司值函数参数

图4显示不同的模式转换强度下的博弈中投资公司的效益。可以看出，随着λ1增大时，投资公司效益降低。而当λ2增大时，投资公司效益增加。

3 结论

在传统的养老金管理问题中，以往的文献一般关注的是投资策略选择问题。把养老计划的参与者设置为被动的，即他们没有退出养老计划的意愿或者以前支取养老金的权利。本文采用了一种较为新的模型，即Josa等[14]所提出的工会——投资公司养老金博弈模型。作为博弈的参与者之一，投资公司是传统的框架下的基金管理者，它决定了投资的风险敞口。另一个博弈的参与者是工会，它是基金的所有者且可能会不信任基金管理者。假设工会有权利抽取基金的盈利部分，也就是提前支取养老金，在考虑金融市场出现结构性变化的情况下工会与投资公司的博弈策略选择问题。我们给出一个非对称的博弈模型，得到了Nash均衡解。根据理论分析，在没有模式转换的情况下得到了Nash均衡解的完全解析形式，同时得到模式转换下的解与无模式转换的解的关系。通过分析风险厌恶系数与模式转换强度对均衡策略的影响，得到如下的结论：

(1) 采用CRRA模型时，得到工会抽取基金盈余的比率是一个常数，与风险厌恶系数、市场情况和模式转换强度有关。投资公司的投资策略与莫顿模型一致，且不受模式转换的影响。

(2) 在牛市中，工会抽取基金盈余的比率较大，而在熊市中，工会抽取比率较小。这是因为工会想要分享市场繁荣带来的利益。这种趋势随着模式转换强度的增加而减弱。