覆冰导线驰振时其极限环幅值反馈控制
2020-11-24闵光云刘小会1孙测世蔡萌琦
闵光云, 刘小会1,*, 孙测世, 蔡萌琦
(1.重庆交通大学土木工程学院, 重庆 400074; 2.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室, 重庆 400074;3.成都大学建筑与土木工程学院, 成都 610106)
覆冰导线的驰振是一种典型的自激振动,由于其驰振形状类似于龙舞,因此又称舞动,其主要特点表现为小变形、大位移[1-3]。在雨凇、霜淞等恶劣环境下驰振的持续时间可长达数十日,导线驰振会产生交变张力,大幅变化的交变张力易使得导线疲劳、金具磨损,严重时可导致结构功能失效。针对驰振所产生的交变张力问题,王少华等[4]采用仿真与理论结合的方法研究了覆冰导线的舞动特性并讨论了物理参数对动态张力的影响。黄欲成等[5]采用能量平衡法分析了导线Bate阻尼线体系的微风振动特性,其研究成果表明交变张力可改变输电导线的防振特性。针对导线的驰振机理问题,不同的学者建立了不同的模型,提出了不同的驰振机理,但目前学术界普遍接受的还是Hartog[6]提出的竖向失稳机理,以及Nigol等[7]为代表的学者提出的竖向-扭转二自由度耦合的舞动机理。基于提出的驰振机理,再根据试验或者仿真得到导线的三分力气动参数,接着就能研究导线的舞动特性。蔡萌琦等[8]首先进行了覆冰八分裂导线的风洞试验,接着通过ABAQUS用户子单元施加气动荷载,研究了覆冰八分裂导线的舞动特性。向玲等[9]采用流体计算软件模拟了覆冰四分裂导线各子导线的气动参数,接着将四分裂导线等效为绕中心轴的一根导线,基于驰振控制方程分析了四分裂导线的舞动特性。
在以上学者们的研究基础上[1-14],推导单挡导线驰振控制方程,通过风洞试验得到覆冰导线的三分力气动参数,基于多尺度法求解覆冰导线发生驰振时产生的极限环的表达式,最后通过引入线性、平方非线性、三次非线性反馈控制器实现对极限环幅值的控制。
1 单挡导线驰振方程
为推导单挡导线的驰振控制方程,首先建立单挡导线力学模型,如图1所示。图1中,青色曲线表示导线的静态平衡构型,其上的微元用ds表示;蓝色曲线表示导线在外部荷载作用下的动态构型,其上的微元用ds′表示。y表示导线竖向的静态位移,w表示导线竖向的动态位移,x表示导线横向的静态位移,u表示导线横向的动态位移。

图1 单挡导线力学模型Fig.1 Mathematical model of single conductor
假设导线为连续体,分别在导线静态平衡构型与动态平衡构型上取出一微元段,如图2所示。
图2中,T表示导线静态张力;Q、Q′分别表示导线静态构型、动态构型上微元段所受剪力;M、M′分别为导线静态构型、动态构型上微元段所受弯矩;τ为动张力。

图2 导线微元图Fig.2 Micro element diagram of conductor
列出导线y轴方向静力平衡方程,即
(1)
式(1)中:m表示导线单位质量;g表示重力加速度。
列出扰动状态下导线的动态平衡方程,即

(2)
由材料力学可知:
(3)
式(3)中:EI表示弯曲刚度;w″表示对位移x求二阶导数。
假设导线垂度很小,且u沿x轴方向变化不大,即
(4)
联立式(1)~式(4)可得:
(5)
式(5)即考虑抗弯刚度的动力学方程。
动张力的表达式为
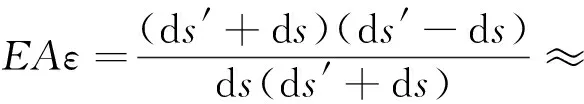
(6)
忽略导线轴向的惯性力,可将动张力表示为
(7)
将式(7)代入式(5)可得:
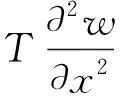
(8)
式(8)中:fc表示阻尼系数;Fair表示空气荷载,其表达式为
(9)
式(9)中:ρ为空气动力系数;D为导线迎风直径;U为当地平均风速;Cy(α)为气动参数,其表达式为
Cy(α)=α1α+α2α2+α3α3
(10)
式(10)中:α1、α2、α3需通过风洞试验获得;α为瞬时攻角,其表达式为
(11)
式(1)中:α0为初始攻角;θ为扭转角。
导线的驰振特征主要由基本模态决定,因此可将导线的动态位移写为
w=φ(x)q(t)
(12)
式(12)中:φ(x)表示模态函数;q(t)为时间函数。
将式(9)~式(12)代入式(8)并结合Galerkin离散法可得:
(13)
式(13)中:
为方便使用多尺度法分析,现转化式(13)的表达式为
(14)

2 风洞试验
为确定导线的覆冰类型以及与风洞试验相关的各项参数,于2008年到四川省西昌市对覆冰导线进行观测调研。图3所示为导线的覆冰类型,主要表现为新月形冰型。

图3 现场调研所得导线覆冰冰型Fig.3 Iced type of conductor obtained from investigation
覆冰模型的材料采用木头,按实际形状进行加工,然后粘贴在导线模型表面,如图4所示。

图4 覆冰冰型模型Fig.4 Ice covered model
采用拟静态方法,选取一段导线模型,进行气动参数测试,测试模型如图5所示。

图5 覆冰单导线舞动模拟试验模型Fig.5 Galloping simulation model of iced single conductor
通过风洞试验测得12 mm冰厚的新月形覆冰单导线在10 m/s风速作用下三分力系数随瞬时攻角的变化曲线,如图6所示。

图6 覆冰单导线空气动力系数Fig.6 Aerodynamic coefficients of iced single conductor
3 多尺度法求极限环
针对非线性振动系统的研究方法有多种,但多尺度法是比较传统的方法,且覆冰导线的驰振属于弱非线性振动,因此选取多尺度法。为方便覆冰导线驰振方程的处理,引入式(15):
(15)
覆冰导线的驰振属于弱非线性振动系统,因此式(14)可改写为
(16)
根据多尺度法可将式(16)的解设为
x=x0(T0,T1)+εx1(T0,T1)+…
(17)
式(17)中:T0、T1表示两个时间尺度,(T0=t,T1=εt)且满足:
(18)
将式(17)代入式(18)可得:
(19)
将式(19)代入式(15),并将涉及ε0项的系数、ε1项的系数分别整理在一起,即
ε0阶:
(20)
ε1阶:

κ4(D0x0)2+κ5(D0x0)3
(21)
令:
x0=A(T1)exp(iω0T0)+cc
(22)
式(2)中:cc表示式(22)共轭项。
将式(22)代入式(21)可得:

(23)
根据微分方程的可解条件,求解式(23)首先需消除其永年项,即
(24)
为方便计算,先引入极坐标函数:
A(T1)=0.5aexp(iφ)
(25)
式(25)中:a表示幅值;φ表示相位;i为虚数单位。
将式(25)代入式(23)并且分离虚部可得到平均方程为
(26)
针对求解系统稳态解的问题,令式(26)左端为0,即可得到:
(27)
4 反馈控制器
4.1 线性反馈控制器
(28)
同样运用多尺度法可得式(28)的稳态解为
(29)
观察式(29)可得知:当κ=0时,式(29)即等价式(27),即未受控的下覆冰导线驰振的极限环表达式;当κ=-κ3时,可将幅值控制到0。
4.2 二次非线性反馈控制器
(30)
同理,运用多尺度法可得式(30)的稳态解为
(31)
观察式(31)可知其与式(27)完全一样,即二次非线性反馈控制系统对覆冰导线驰振下的幅值不起控制作用。
4.3 三次非线性反馈控制器
(32)
同理,运用多尺度法可得式(32)的稳态解为
(33)
观察式(33)可得知:当κ=0时,式(33)即等价式(27);当κ=-κ5时,可将幅值控制到0。
5 算例分析
根据以上分析可知,线性反馈控制器、三次非线性控制器皆能控制覆冰导线驰振时所产生的幅值。为了验证理论结果的正确性,下面将通过具体的数值算例给出解释。导线的物理参数如表1[14]所示,模态函数选取φ(x)=sin(πx/l),导线长度l为300 m。

表1 导线的物理参数Table 1 Physical parameters
根据以上导线的物理参数以及风洞试验所得的三分力气动系数并基于MATLAB可得覆冰导线驰振下受控与不受控的极限环,如图7所示。
观察图7可知,不论是线性反馈控制器还是三次非线性反馈控制器皆能控制覆冰导线驰振下所产生的极限环的大小,针对具体的覆冰导线选取合适的反馈控制函数完全能使得导线的幅值为0。
为了更加清晰地分析反馈控制器对幅值的控制效果,下面给出了导线处于稳定状态下任意10 s的位移时程曲线,如图8所示。
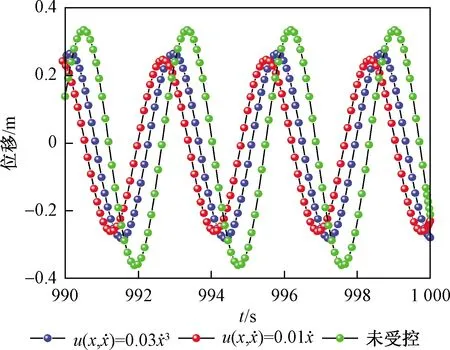
图8 舞动时程曲线Fig.8 Time history curve of galloping
观察图8可以发现,反馈控制器在不改变系统的周期的前提下能对导线的幅值起到明显的抑制作用。由于导线的幅值随着κ的变化而变化,因此针对具体的覆冰导线选取合适的κ能将其驰振所产生的幅值降为最小,从而保证工程的安全。
6 结论
根据研究,所得结论如下。
(1)将导线假设为连续体,推导了导线驰振方程,进行了风洞试验,所得的三分力气动参数能给以实际工程一定的参考价值。
(2)通过多尺度法求得了导线驰振下所产生的极限环的表达式,通过引入线性反馈控制函数与三次非线性反馈控制函数降低了极限环的幅值,进而能保证工程结构的安全运行。
