扇形太阳电池阵折展机构模态及谐响应分析
2020-11-24孟少华张立建高兴文张丹丹
李 健,胡 明*,孟少华,张立建,高兴文,张丹丹
(1.浙江理工大学 机械与自动控制学院,杭州310018;2.北京卫星环境工程研究所,北京100094)
0 引言
太阳电池阵作为大多数地球轨道航天器的能量获取装置,其稳定工作对于航天器的安全有效运行具有重要意义。而太阳电池阵折展机构作为太阳电池阵展开的核心机构,其固有振动特性将会对太阳电池阵的在轨可靠性产生重要影响。Fu J 等[1]分析并验证了太阳电池阵内部蜂窝板结构的频率,为电池阵结构优化和改进提供了重要参考。李郑发等[2]重点考虑支撑点对折叠太阳电池阵固有特性的影响,优化了支撑点的位置分布。魏进[3]基于Ham ilton原理建立系统动力学模型,分析多基板铰接而成的大型太阳电池阵的固有频率和全局模态。曹登庆[4]以大型柔性航天器为研究对象,采用全局模态分析方法建立系统的非线性动力学模型,得到可表征铰链转动和太阳电池阵弹性振动的系统全局模态。刘少锋[5]以太阳电池阵基板为研究对象进行正弦振动试验,其结果与模态分析结果基本一致。黄俊等[6]以折叠太阳电池阵为研究对象,重点考虑锁销连接位置设计对于展开后的太阳电池阵固有振动特性的影响,通过试验对比验证锁销间隙对电池阵刚度特性的影响规律。雷勇军等[7]针对太阳电池阵的空间特殊结构形式,考虑单块基板以及多块组合基板的不同设计,得出其相应的模态参数计算方法。朱兴高等[8]以太阳电池阵驱动机构为研究对象进行谐响应分析,为太阳电池阵驱动机构地面试验提供参考。以上工作研究了太阳电池阵蜂窝板结构、局部支撑点、锁销连接位置、驱动机构等单独部件的固有振动特性。
本文设计了一种新型扇形太阳电池阵折展机构,其具有质量小、折展比大等优点,且可重复折展。为研究该折展机构的固有振动特性,对其进行模态和谐响应分析,首先利用有限元方法对扇形太阳电池阵折展机构展开后锁定状态的三维数字模型进行六面体网格划分,然后进行模态分析得到机构整体的固有频率,并采用模态叠加法对太阳电池阵展开机构进行谐响应分析,获得其危险节点在简谐激励作用下的频率‒位移响应曲线。本研究结果可为太阳电池阵折展机构的结构设计提供参考,实现结构优化,减小振动幅值。
1 扇形太阳电池阵折展机构简介
扇形太阳电池阵折展机构主要由太阳电池阵支撑架总体、动力装置、柔性带传动机构、轮系展开/收拢机构、旋转导板和楔块锁解机构组成。其初始收拢状态如图1所示。

图1 折展机构初始收拢状态Fig.1 Structure of the mechanism in initial folded state
在进入预定轨道之前,折展机构保持收拢状态并与航天器本体锁紧。进入预定轨道后,电机解锁并通过柔性带传动机构及行星轮系驱动旋转导板绕行星架中心逆时针旋转,从而实现扇形太阳电池阵呈扇面展开,见图2。完全展开到位时,旋转导板上固连的楔块插入到固定板上的楔块锁解机构中,完成太阳电池阵支撑架总体的定位、锁定动作。当航天器需要变轨时,折展机构执行收拢动作,楔块锁解机构解锁释放楔块,电机通过柔性带传动机构及行星轮系驱动旋转导板顺时针旋转,从而实现扇形太阳电池阵支撑架折叠收拢。重复折展动作流程如图3所示。

图2 折展机构完全展开状态Fig.2 Structure of themechanism in fully expanded state

图3 折展机构重复折展动作流程Fig.3 Flowchart of repeated folding action with solar array folding mechanism
2 扇形太阳电池阵折展机构的模态分析
2.1 折展机构有限元网格划分
建立折展机构三维数字模型导入到HyperMesh软件中,以行星轮轴线向上指向为x轴正方向,根据右手法则建立空间坐标系。依据折展机构展开锁定的实际工况简化其整体结构,简化过程如下:展开锁定后,锁定模块采用全约束边界条件,选用rbe2单元固连;模块之间铰链保留其转动自由度,铰链部分采用bar 单元;对机构模型进行网格划分,网格单元选择六面体单元。模态分析和谐响应分析不考虑柔性体,扇形太阳电池阵折展机构各刚性构件的材料参数设置为:
1)支撑架总体、楔块和旋转导板的材料为6061铝合金,其弹性模量为7.00×104MPa,密度为2.84×103kg/m3,泊松比为0.31;
2)行星架、行星齿轮和带轮的材料为45#钢,其弹性模量为2.07×105MPa,密度为7.83×103kg/m3,泊松比为0.30。
2.2 折展机构约束模态分析
模态分析是分析机械结构的固有振动特性的重要方法之一,用来考察结构每一阶模态具有的特定固有频率、阻尼比和模态振型等[9]。考虑到扇形太阳电池阵折展机构稳定的展开锁定状态是太阳电池阵正常工作的基础,在折展机构展开锁定状态下的各个铰链连接处施加全约束,将其作为模态分析的边界条件,分析得到折展机构的前20阶固有频率(见表1)和模态分析振型(见图4)。

表1 太阳电池阵折展机构前20阶固有频率Table1 The first 20natural frequencies of the solar array folding mechanism


图4 太阳电池阵折展机构前20阶模态分析振型Fig.4 Modal analysisof the first 20 modes of the solar array folding mechanism
由表1可知:1)固有频率随着振型阶次的提高而不断增大,这是由于在载荷能量固定的前提下,随着阶次的提高,能量减弱不足以激发更高阶的振动,同时高阶振动的节点数增加,所以振动不易激发产生;2)6.47~11.62 Hz和36.49~41.22 Hz 频率范围内,相邻两阶的固有频率比较接近,容易产生模态混叠现象。
由图4可知:1)机构在6.47~11.62 Hz 频率范围内,出现整体弯曲变形;2)在36.49~41.22Hz 频率范围内,折展机构旋转导板会发生扭曲变形。说明折展机构在较低的固有频率下会出现整体的弯曲变形,在较高的固有频率下会出现局部的扭曲变形。两者比较可知,扇形太阳电池阵折展机构在高阶模态更容易出现集中变形。
3 扇形太阳电池阵折展机构谐响应分析
谐响应分析是指在模拟机构整体受到随时间以正弦规律变化的载荷条件下,确定线性结构所表现出来的稳态响应[10]。根据模态分析中折展机构前20 阶固有频率区间范围,设置加载频率的范围为1~65 Hz,并根据模态分析结果选取折展机构中2个容易发生变形的部件上的3个危险节点作为监测点,分别为大带轮转动节点N158505、太阳电池阵支撑板节点N24847和N31185(见图5)。谐响应分析时在节点N24847处x方向施加幅值大小为l N、随时间以正弦规律变化的载荷。
采用模态叠加法进行分析,通过OptiStruct 软件获得上述3个节点的频率‒位移曲线,如图6~图8所示。由谐响应分析结果可知:1)大带轮转动节点N158505的振动幅度相比太阳电池阵支撑板的较小,位移峰值21.35mm 出现在43.23 Hz 频率处,在大带轮的设计上应当注意此点;2)太阳电池阵支撑板节点N24847的位移峰值263.25mm 出现在22.14 Hz 处,节点N31185的位移峰值262.75mm出现在41.04Hz 处,因此应当在适当范围内增加太阳电池阵支撑板的质量,以减小振动幅度。
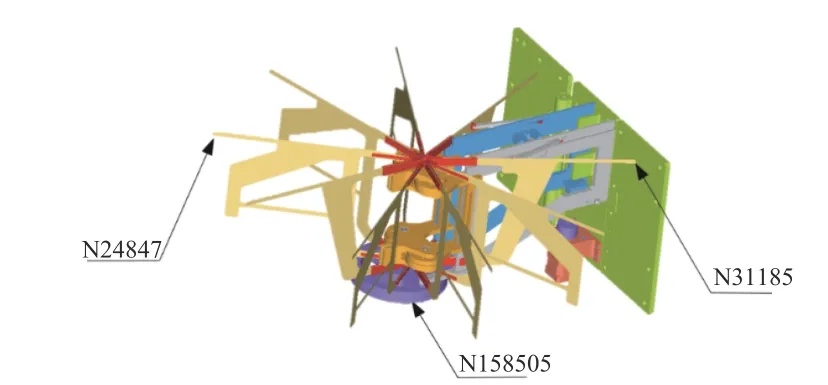
图5 谐响应分析模型Fig.5 Harmonic response analysismodel

图6 大带轮转动节点N158505的频率‒位移曲线Fig.6 Frequency-displacement curve of large pulley rotation node 158505

图7 太阳电池阵支撑板节点N24847的频率‒位移曲线Fig.7 Frequency-displacement curve for node 24847 on solar array mounting plate

图8 太阳电池阵支撑板节点N31185的频率‒位移曲线Fig.8 Frequency-displacement curve for node31185 on solar array mounting plate
4 结论及建议
本文通过对扇形太阳电池阵折展机构进行模态分析,研究其固有振动特性,得到该机构前20阶固有频率;并基于模态叠加法对该折展机构进行谐响应分析,获得若干危险节点在简谐激励作用下的频率‒位移曲线,从而得到如下结论:
1)在6.47~11.62 Hz和36.49~41.22 Hz 频率范围内,折展机构相邻两阶的固有频率差值较小,易出现模态混叠现象,应在折展机构的结构优化设计中予以关注。
2)所分析的3个危险节点在简谐激振力作用下的谐响应峰值位移出现在11.54~50.00Hz 范围内,其中太阳电池阵支撑板振动幅度较大,因此应在允许范围内适当增加太阳电池阵支撑板的质量,以减小振动幅度。
