三轴六自由度闭环虚拟随机振动试验系统建模与仿真

韩 伟，李敏伟，孙建勇，齐亚超，王克强，马 英

（中国航空综合技术研究所，北京100028）

0 引言

三轴六自由度试验技术是国内外振动试验技术的一个新的发展方向。采用计算机仿真的方法来模拟三轴六自由度振动试验的过程，通过虚拟试验结果找出最佳控制策略，可以指导真实试验，克服试验局限，提高试验效率。目前，国外已针对虚拟试验技术和应用开展了多年的研究，取得了丰硕成果。如ESA/ESTEC（欧空局/欧洲空间技术试验中心）为其振动试验系统实物建立了虚拟系统，该系统将振动台、功率放大器与控制器、试验件等子系统模型集成在一起，形成一个多系统集成的虚拟振动试验系统，来指导实施实物振动试验[1]。国内也对虚拟振动试验技术进行了研究，主要是利用有限元方法建立振动台、夹具和产品的模型，然后进行产品的虚拟振动试验；虚拟试验研究主要集中在多台单轴向虚拟振动试验[2]和两点激励虚拟振动试验[3]。

相比较而言，三轴六自由度振动试验是一种实施过程复杂、技术难度大、控制要素多的多维振动试验，其控制目标为6×6维矩阵，对试验设备和试验控制方案要求较高。在实物振动试验之前利用虚拟振动试验系统进行仿真，可获得试验件振动响应，从而有效避免过试验或欠试验。但目前国内外对三轴六自由度虚拟振动试验的研究较少。

本文基于中国航空综合技术研究所三轴六自由度实物试验系统，建立了一套三轴六自由度闭环虚拟振动试验系统，以用于多输入多输出（M IMO）振动系统控制方案设计。

1 三轴六自由度虚拟振动试验系统概述

三轴六自由度虚拟振动试验系统（如图1所示）由虚拟的振动台、多维振动控制器、台面、试验件和夹具等构成。其中：多维振动控制器生成8路驱动电压信号经放大后输入振动台，通过静压轴承、夹具等使虚拟台面产生振动；台面4个控制点上的加速度响应经坐标变换后反馈到振动控制器，控制器再对各控制点的自功率谱密度（或幅值）、相干系数和相位等与参考谱进行比较和修正，使得虚拟台面上产生的加速度响应谱符合试验条件的要求。

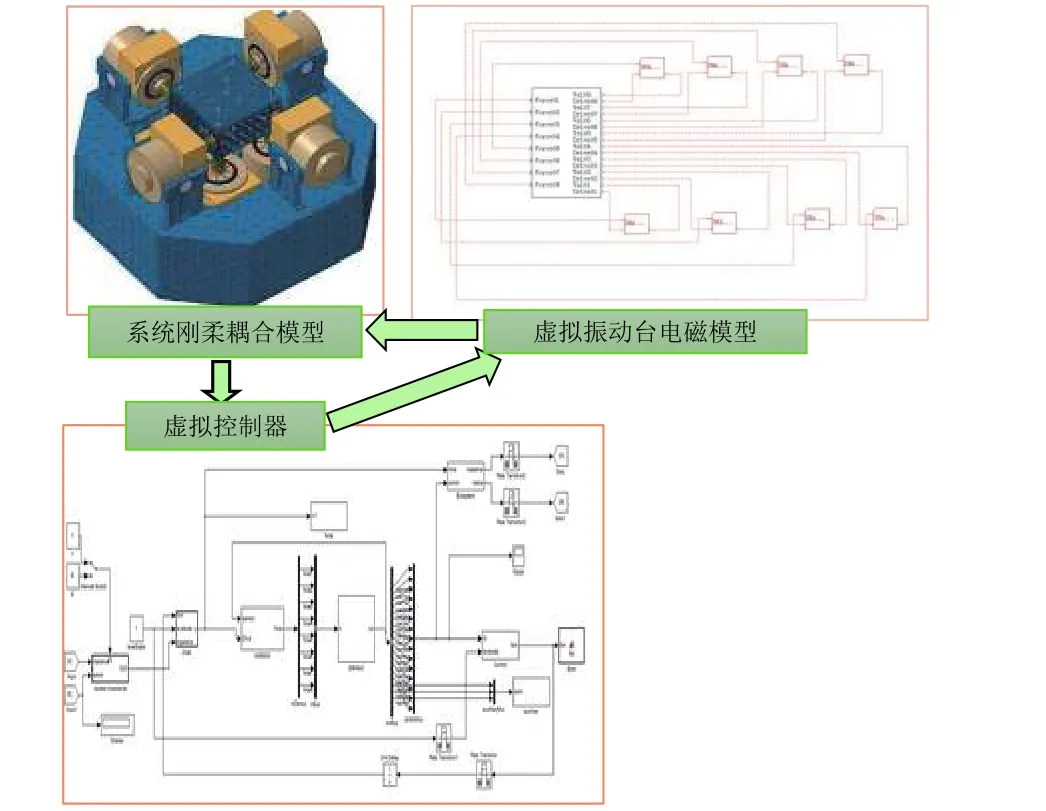
图1 三轴六自由度闭环虚拟振动试验系统Fig.1 The three-axis six-DOF closed loop virtual vibration system

三轴六自由度闭环虚拟随机振动试验系统的建模首先需要建立各组成部分的机械和电磁有限元模型，然后按照实物试验系统（见图2）物理与信号关系将各组成部分装配成完整的虚拟系统。具体步骤如下：1）虚拟振动台建模；2）虚拟控制器开发；3）虚拟台面建模；4）三轴六自由度虚拟振动试验系统装配。

图2 三轴六自由度振动试验系统实物Fig.2 The three-axissix-DOFvibration system

2 三轴六自由度闭环虚拟随机振动试验系统建模

2.1 虚拟振动台建模

虚拟振动台建模主要包括机械和电磁系统两部分[4]，电磁模型预留虚拟控制器的仿真接口，振动台可与静压轴承、台面、试验件和夹具等部件装配成为完整的三轴六自由度虚拟振动试验系统。

振动台机械部分使用二自由度集中参数法（简化为台体、动圈和线圈）建模[4]，具体如下：

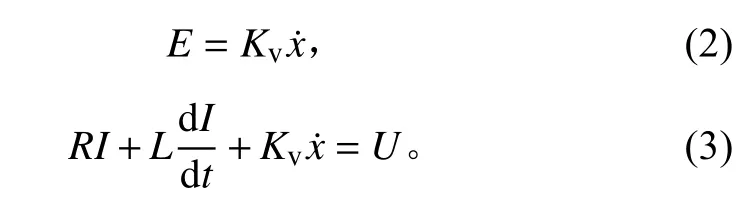
其中：F为电磁力；Kf为电振动台的推力常数；I为线圈中的电流，A；E为线圈两端产生的感应电压；Kv为比例系数；x˙是线圈相对于磁场的运动速度；R为线圈的电阻，Ω；L为线圈的自感系数，H；U为施加在线圈两端的电压，V。

虚拟振动台参数，一部分可通过振动台生产厂家提供得到，其他的可对比实测频响数据修正得到。本文通过参数识别得到的振动台模型参数见表1。

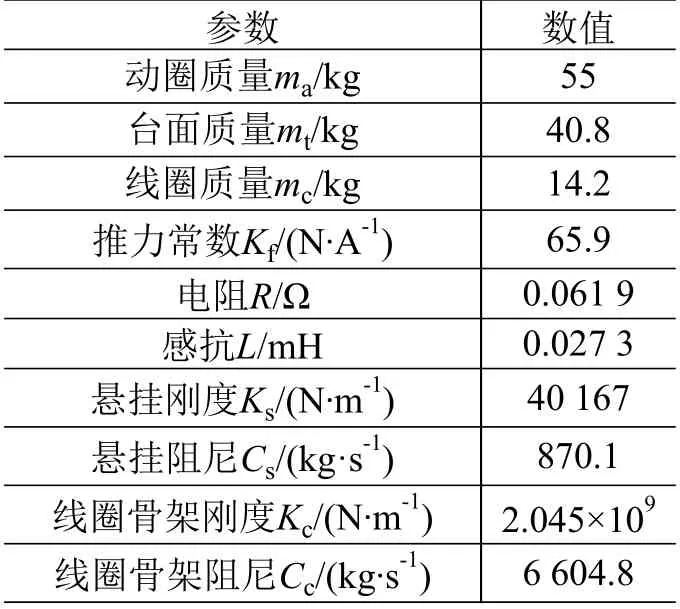
表1 虚拟振动台模型参数Table1 Parameters of thevirtual vibration table model

2.2 虚拟控制器开发

虚拟控制器的开发是三轴六自由度虚拟振动试验系统建模的关键。虚拟随机振动控制器基于SimuLink 软件开发，本文仅给出其开发内容，主要包括频响函数估计模块、互谱密度矩阵估计模块、修正模块和驱动信号生成模块等。

驱动信号的生成需要系统的阻抗矩阵，阻抗矩阵可以通过系统频响函数矩阵求逆得到。本文基于H1估计方法开发虚拟系统的频响函数估计模块，由激励信号d和响应信号y可得到频响函数矩阵的H1估计，即

式中：H为估计得到的系统频响函数矩阵；S yd为各响应信号y和激励信号d的互谱密度矩阵；S dd为各激励信号d的自谱密度矩阵。

虚拟控制器根据阻抗矩阵和用户设置的参考谱矩阵，经驱动信号生成模块计算得到1帧驱动信号，分别向各轴向虚拟振动台发送；各振动台对虚拟台面同时施加激励，通过虚拟台面上的响应加速度信号经互谱密度矩阵估计模块得到响应谱矩阵；与参考谱进行对比（相减），参考Underwood 自适应控制算法[5]，经修正模块得到修正更新后的驱动信号。其中，修正算法为

式中：αn为第n步的优化控制增益；ND为第n步的牛顿梯度矩阵，可通过最速下降方法得到；F(E rr,G)为与E rr和G相关的误差矩阵；E rr为响应谱矩阵和参考谱矩阵的实时差值；G为实时估计得到的阻抗矩阵。

2.3 虚拟台面建模

由于实物试验系统的台面中填充了阻尼材料，所以结合锤击法测得的主要模态对虚拟台面参数进行修正，其中：材料的泊松比依然使用实际泊松比；材料密度根据实际质量和体积进行调整；弹性模量根据测得的模态频率调整；内部孔径尺寸也进行调整；阻尼参数根据实物模态试验结果确定。由于在虚拟试验时引入较多的模态会导致仿真耗时较长，同时根据计算分析，前3阶模态结果能够保证较高的仿真精度，所以仅给出台面自由状态下实测和仿真模态试验的前3阶对比分析结果（见图3），其模态频率对比结果见表2。

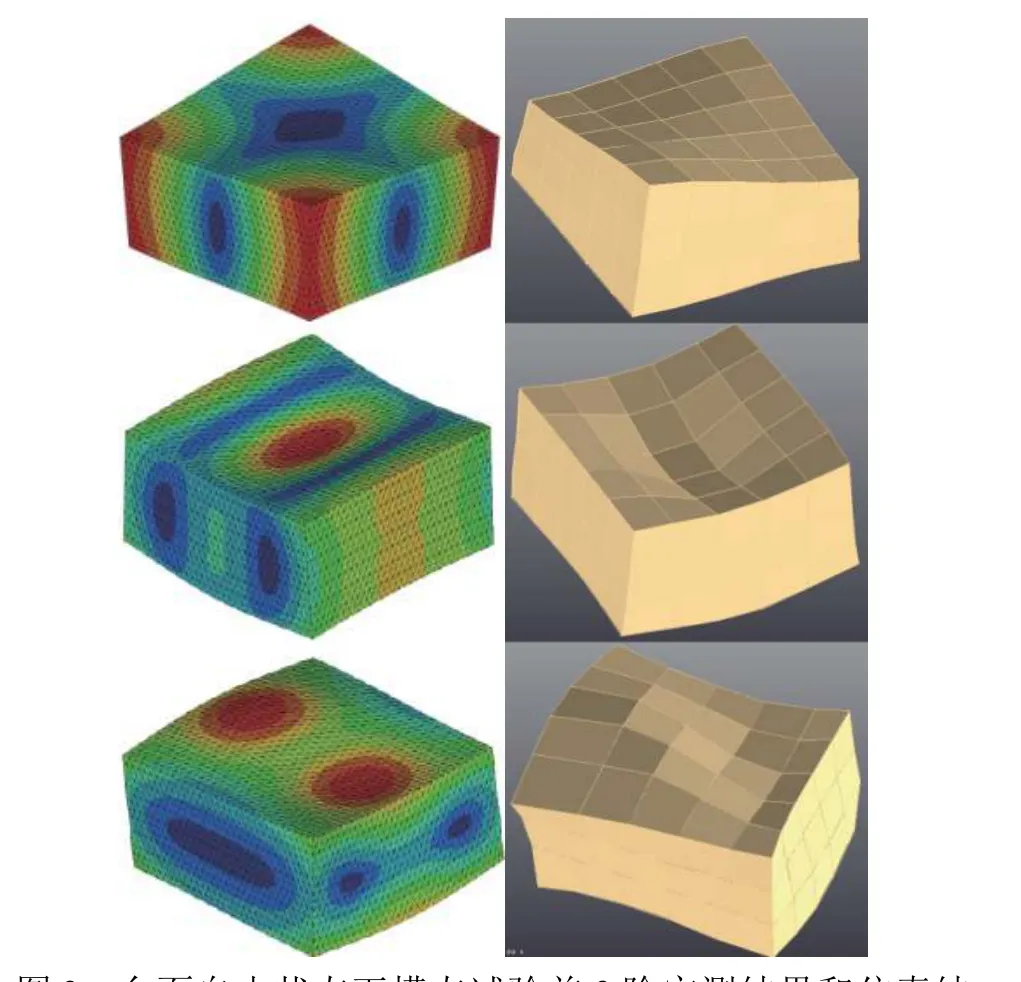
图3 台面自由状态下模态试验前3阶实测结果和仿真结果对比Fig.3 Comparison between the modal test results and simulation results of the first threemodes in free state of the table

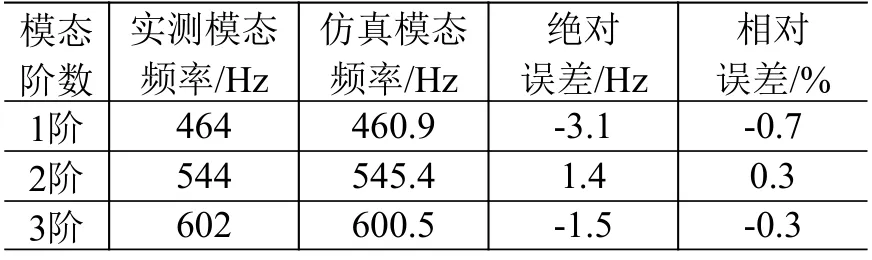
表2台面实物和仿真模态频率对比Table2 Comparison of modal frequency of the table inmodal test and simulation test

由图3和表2可知，三轴六自由度台面的模态实测和仿真试验得到的前3阶模态频率相差不超过5 Hz，各阶模态振型也高度一致，说明上述虚拟台面模型可用于虚拟试验。

2.4 虚拟试验系统装配

在完成了虚拟振动台、虚拟台面、虚拟控制器以及基座、静压轴承等部分的建模后，对三轴六自由度虚拟随机振动试验系统进行装配。该系统使用8 个振动台对虚拟台面进行激励，装配过程中认为各个振动台的各项属性一致，各个静压轴承也都相同。系统装配完成后，进行刚体动力学仿真，然后对台面等部分进行柔性化处理，建立虚拟试验系统模型。

模型建立后，将虚拟控制器发出的8路驱动电压信号传递给振动台的电磁模型（可基于SimuLink或AMEsim）；通过设定通信步长将SimuLink 中的电压信号传送到S-function，即振动台电磁模型，在电磁模型中产生电磁力；电磁力和刚柔耦合模型相互作用，形成闭环虚拟随机振动试验系统。

3 虚拟试验结果评价

虚拟试验系统模型建立后，需要找出最优的控制方案，这涉及对不同控制方案下虚拟试验结果的评价。评价是基于响应谱密度矩阵对参考谱密度矩阵的偏差情况作出，一般采用局部误差和全局误差[6]分别表示单个自由度控制效果和多自由度振动严酷度的总体控制情况。局部误差和全局误差包括各自由度的自谱误差和各自由度间的互谱误差（相干系数和相位）。除上述频域误差以外，对于振动量值，还包括各自由度局部均方根误差和全局均方根误差。以上误差中，自谱的局部和全局误差较重要，体现的是各自由度的自谱的局部和全局偏离程度，因此本文仅对其进行说明，相干、相位谱误差分析方法以及均方根误差分析方法与自谱的局部和全局误差的类似。

3.1 三轴六自由度的自谱局部误差

自功率谱密度（ASD）局部误差一般用相对误差来表征，计算方法同单自由度，具体为

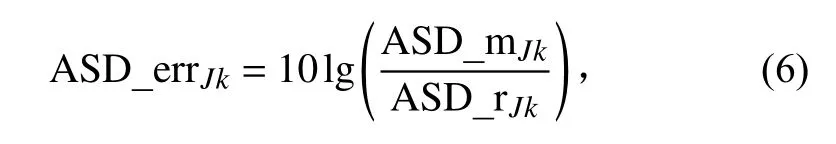
式中：ASD_errJk、ASD_mJk和ASD_rJk为第J个自由度第k个谱线处的自功率谱的误差（单位dB）、实测响应自谱量值和参考自谱量值。

3.2 三轴六自由度的自谱全局误差

三轴六自由度的自谱全局误差通过构建正则化权重矩阵对各自由度的自谱局部误差进行加权平均得到，具体计算过程如下：

1）假定三轴六自由度随机振动自谱的实测值和参考谱量值分别为：

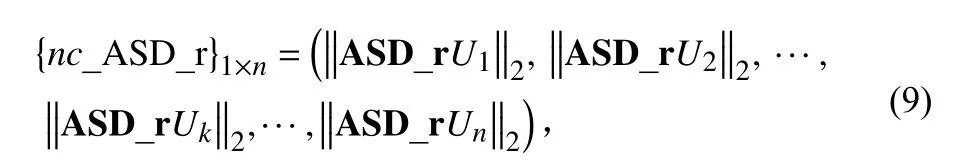
其中：n为谱线数；Uk为n×n维单位矩阵的第k列；矩阵ASD_r 乘以Uk，将分离出自谱第k个谱线处的各个自由度谱值。

2）使用式(8)和式(9)对参考谱密度矩阵ASD_r 每一项对应的权重进行计算，计算时结合参考谱矩阵和相对应的2-范数对列向量进行正则化处理，

其中Wt6×n为6×n维权重矩阵。

权重矩阵是结合三轴六自由度各谱线处的参考谱值大小提出的，其总体思想是，各自由度自谱大的量值（振动严酷度大）在误差分析中权重大，自谱小的量值在误差分析中权重小。

3）使用式(10)权重矩阵对式(6)所示的自谱误差矩阵进行正则化处理，得到正则化误差矩阵为

对式(11)每一列求和，即可得到自谱在各个谱线处的全局误差为

综上所述,对肾结石手术患者进行优质护理服务,使患者术后的康复速度加快,住院时间缩短,生存和生活质量大大提高,患者满意度高,因此值得在临床应用上广泛推广。

式(12)中含有全部自由度的自谱量值信息，表征了六自由度随机振动实测自谱量值与参考自谱量值在各谱线上的整体偏离程度。应注意，权重矩阵中每一列的和为1，这说明式(12)得到的自谱的全局误差即为多自由度自谱局部误差的加权平均，权重就是在各谱线处单个自由度占所有自由度2-范数的权重。

上述试验结果评价方法将用于对虚拟试验不同控制方案的评价和最优方案的选择，以及方案是否可用于实物试验的判定，以防止实物试验中出现过试验（如因自谱的局部误差过大导致试验件经历较大的试验量级而损坏试验件）或欠试验，降低试验风险。

4 三轴六自由度虚拟随机振动试验仿真

4.1 虚拟试验条件和试验结果

基于建立的三轴六自由度虚拟随机振动试验系统进行仿真，并采用基于局部和全局误差的试验结果评价方法对虚拟试验结果进行评价，选择最优控制方案。

本文采用坐标变换的方法得到三轴六自由度振动响应，台面中心处的三轴向平动自由度x、y、z的ASD和转动自由度θx、θy和θz的角加速度ASD，它们代表了各轴向振动严酷量值，非对角元素表示各自由度之间的互谱，由于互谱很难确定，为方便起见，在进行虚拟试验时，假定各自由度互不相关，即虚拟试验暂不考虑互谱关系，矩阵的非对角元素均设定为0，具体为

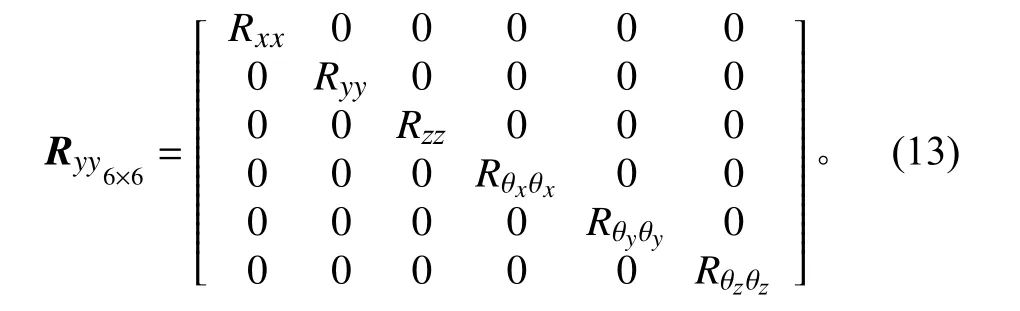
采用4个三轴向加速度计作为控制传感器，传感器安装在虚拟台面的4个边角附近，通过坐标变换的方式实现三轴六自由度随机振动控制，试验条件设计如下：

1）试验谱型使用宽带随机平直谱，频率范围5～2000Hz。

2）试验量值为：3个平动自由度的振动均方根值为10g，3个转动自由度最大振动均方根值为98 rad/s2。

3）各自由度之间的互谱密度为0，相干谱均设定为0，相位谱均设定为0°。

按照上述试验条件进行三轴六自由度虚拟随机振动试验，试验结果见图4。

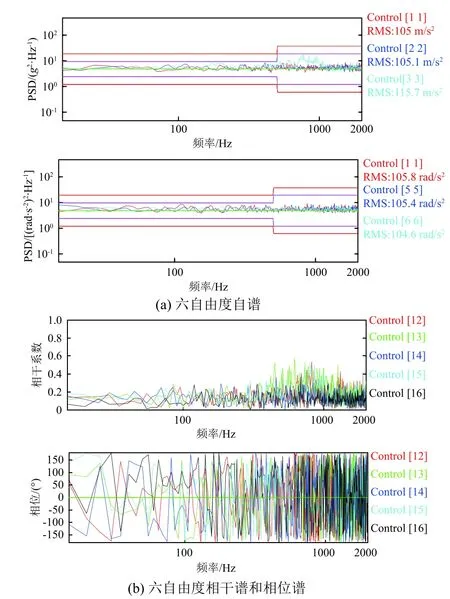
图4 三轴六自由度虚拟随机振动试验控制结果Fig.4 Three-axis six-DOF virtual random vibration test control results

由图4可以看出，在相干谱设置为0的条件下，相位谱是随机变化的。相干谱和相位谱体现的是各自由度之间的关系，跟各自由度所在的结构有关，本文主要考虑了各自由度的能量（自谱）控制，同时假定了各自由度之间的相互关系（相干系数为0）并进行控制，参数的设定跟实际结构的参数有差异，但仿真结果可用于参考。此外，在虚拟试验仿真过程中，可以根据需要观察台面或试验件任意一点的加速度响应和应力场等情况，图5为试验台面上获得的应力场和加速度响应。可以看出，虚拟试验相比实物试验，提供的信息更为丰富，从中可获得加速度、位移、速度和应力等变化情况，并利用这些信息进一步分析结构应力损伤情况，帮助确认试验夹具或试验件在试验过程中是否会损坏，找出其中薄弱环节等。

图5 三轴六自由度虚拟振动试验实时应力场和加速度响应Fig.5 Real-time stress field and the acceleration response in three-axis six-DOF virtual vibration test

4.2 虚拟试验结果评价

基于局部和全局误差的试验结果评价方法分析控制方案下虚拟试验的控制结果，三轴六自由度局部误差和全局误差分别如图6(a)和图6(b)所示，可见：该控制方案虚拟试验控制误差较小，其均方根全局误差在0.2 dB左右，功率谱密度全局误差最大在±2 dB左右，相干全局误差在0.3左右。评价结果表明本试验控制方案能够满足控制容差要求。

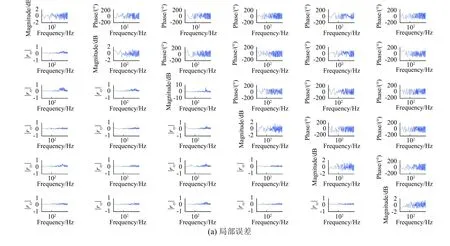
图6 三轴六自由度随机振动试验局部误差和全局误差Fig.6 Local error and global error in three-axis six-DOF virtual vibration test

5 结束语

本文主要对虚拟振动台、虚拟随机振动控制器和虚拟台面进行建模，将3个模型装配成三轴六自由度虚拟随机振动试验系统，然后基于该虚拟试验系统进行三轴六自由度闭环动态仿真。仿真结果显示，三轴六自由度虚拟试验系统建模准确，可以实现虚拟台面的三轴六自由度随机振动功率谱密度矩阵（6×6维）控制，并可基于局部误差和全局误差对控制结果进行评价。该系统可用于三轴六自由度实物试验前的随机振动试验控制方案优化，降低实物试验过程中可能出现的过试验或欠试验风险。