考虑利他行为和服务价值的双渠道供应链动态博弈与复杂性研究
2020-11-23阿布都热合曼·卡的尔金美惠依不拉音·吾斯曼
阿布都热合曼·卡的尔 金美惠 依不拉音·吾斯曼

摘 要:考虑利他行为和服务价值的双渠道供应链动态博弈,分析网络直销渠道和传统渠道销售价格差别定价的市场行为,构建了一个单一制造商和零售商的双渠道闭环供应链模型。基于动态博弈理论、复杂动力学理论,通过倍周期分岔和最大Lyapunov指数描述了模型的动力学特征。研究表明制造商和零售商决策变量的调整速度过快时,系统会进入一种混沌状态。在现实活动中系统的混沌状态意味着决策者无法对价格进行准确分析,导致市场定价偏离正确轨道,降低了整个供应链的利润,为了避免这种情况,采用调整参数的方法对系统的混沌状态进行有效控制。
关键词:利他行为;服务价值;闭环供应链;动态博弈;混沌
中图分类号:F253 文献标识码:A 文章编号:1673-260X(2020)10-0078-07
引言
供应链系统参与者或企业是相互独立、相互影响,又相互依存的,他们之间始终存在利他行为,这就是供应链的内涵。随着人们消费水平的日益增高,消费者越来越重视产品的售后服务,尤其是在家用电器,电子产品等行业。因此本文构建了利他行为和服务价值为一体的双渠道闭环供应链系统,综合分析系统中供应链的定价博弈行为。随着互联网的快速发展,线上购物方式日益完善,也更加符合当代人的需求,许多制造商不仅在传统渠道销售商品,而且开通了网络直销渠道,以便获得更大的利润。根据前瞻产业研究院发布的《中国直销行业经营模式与投资预测分析报告》统计数据显示,截止至2017年中国直销行业市场规模达到2205.5亿元,同比增长6.56%。研究表明,双渠道供应链定价将会达到最优利润,很多学者对于供应链的动态博弈也做了大量研究。Yi Tian,Junhai Ma,LiuWei Zhao等[1-5]研究了双渠道回收闭环供应链动态定价与复杂性研究,当决策变量的调节速度过快时,会使得系统陷入一种混沌无序的状态,可以采用调整参数的方法对混沌进行控制。依不拉音等[6]研究了多渠道供应价格博弈的混沌动力学,进行了理论验证与数据仿真。Yuehong Guo等[7-10]建立了零售商回收的闭环供应链模型,分析了调节参数对系统的影响,从动力学角度解释了非线性的动态博弈行为。
服务价值是指销售商在销售产品实体的同时提供给客户的各种附加服务。在企业营销实践中,随着消费者收入水平的提高和消费理念的变化,消费者不仅注重产品自身的价值,而且更加关注产品的附加值。尤其是在相似产品的质量和性质基本相同或相似的情况下,企业向客户提供的附加服务越完整,产品的附加值越大,客户获得的实际利益就越大,购买的总价值就越大。因此,在提供优质产品的同时,为消费者提供完善的服务成为现代企业市场竞争的新焦点。当消费者处于不同的条件和环境时,有不同的销售渠道供其选择。Dong-Qing Yao等[11]等建立了由两个零售商和一个制造商构成的带有服务价值的供应链模型,适当的服务价值对于供应链成员来说是有利的。Bin Dan等[12]分析了零售渠道的顾客忠诚度对零售商服务和价格的影响,利用Stackelberg博弈模型进行零售服务和价格的最优决策。Yun Chu Chen等[13]的研究表明一味地增加服务成本可能会导致需求减少,所以对于零售商来说不能无限制的提高服务价值。Ruiliang Yan等[14]研究了零售服务在双渠道市场中的战略作用,发现提高零售服务能够有效缓解渠道竞争压力,试图提高在双渠道市场中的供应链绩效。
在制造商和零售商进行定价的过程中,人们也越来越关注利他偏好的各个方面的研究,经济学家已经广泛研究了利他行为对经济的影响。王冬冬等[15,16]研究了利他行为的低碳供应链决策模型,发现制造商和零售商的利他行为都会刺激制造商的碳减排以及零售商进行低碳宣传活动,供应链利润随制造商利他偏好的增加而增加,随零售商利他偏好的增加而减少。王磊等[17]研究了利他偏好、服务与供应链Stackelberg博弈研究。Zehui Ge等[18-22]研究了供应链中成员的利他行为。他们表明,考虑利他主义的供应链效率介于权力下放和整合情景之间。他们还发现供应商和供应链的效率都得到了提高。孙玉玲等[23]建立了考虑利他主义偏好的供应链模型,发现供应商利他属性的增加有利于零售商和整个供应链系统的收入。虽然零售商利他主义属性的增加对供应商有利,但不利于其自身利润和供应链系统的利润。结果表明,供应商利他主义程度越高,供应链绩效越高;零售商利他主义程度越高,供应链绩效越低。
由国内外文献可见,已有研究只考虑服务价值的闭环供应链系统,或是只研究具有利他行为的闭环供应链系统,考虑其单一的行为。因此本文构建了考虑利他行為和服务价值两种行为下的双渠道供应链模型,系统中加入了利他行为变量和服务成本变量,结合博弈论和动力系统理论,研究利他行为和服务价值对市场的影响,同时采用数值模拟的方法对其进行了数值仿真验证。随着决策变量参数调节速度加快,系统会从稳定状态最终进入混沌状态,采用调节参数控制法,使系统重新回到稳定状态。
1 模型建立
1.1 问题描述与假设
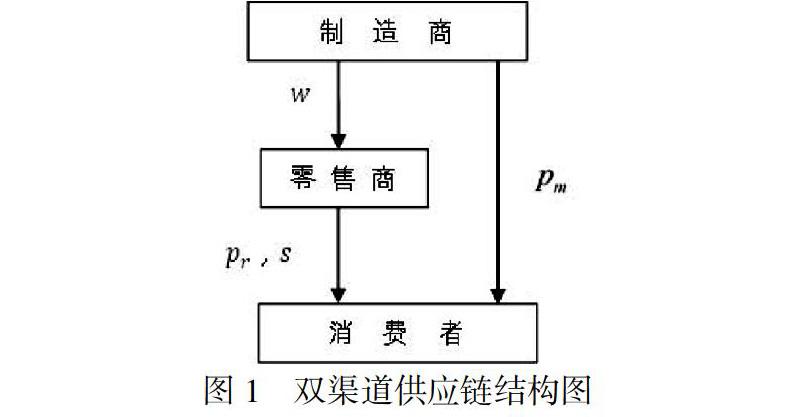
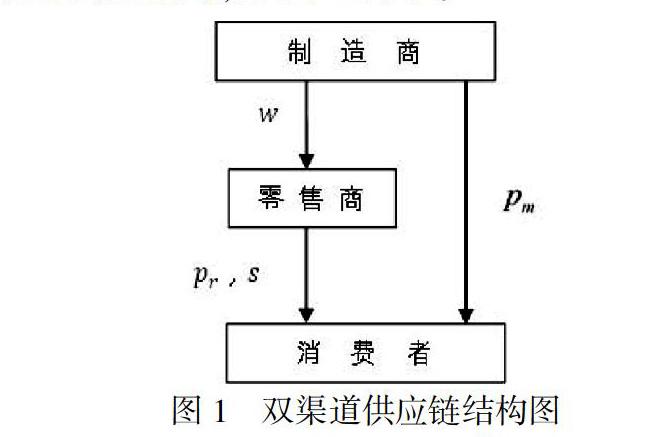
在一个由单一的制造商和零售商组成的考虑利他行为和服务价值的双渠道闭环供应链系统中,传统渠道中制造商以w的价格将产品批发给零售商,零售商在以pr的价格出售给消费者,在直销渠道中制造商直接以pm的价格将产品直接销售给消费者。在决策过程中制造商占主导地位,决策传统渠道的批发价格和网络直销渠道的价格,零售商决策传统渠道的零售价格。由于在传统渠道中,零售商直接面对消费者,存在服务价值,进而会有部分消费者选择传统渠道。同时供应链成员具有利他偏好的行为,所以在进行动态博弈的过程中考虑决策主体的利他偏好,如图1所示。
假设:
(1)在传统渠道中,零售商给消费者提供服务,使消费者具有更好的消费体验。
(2)为了保证零售商是有利可图的,假设零售商的零售价格减去批发价格大于服务价值,即pr-w>s。
(3)直销渠道和传统渠道中的产品是同质的。
(4)供应链成员在进行决策的过程中表现出利他偏好的行为,并且决策目标是自身利益最大化。
1.2 模型的构建
在双渠道闭环供应链中,假设同一商品的渠道忠诚度和渠道价格决定了渠道需求量,根据文献[24]中的线性需求函数,制造商和零售商额的需求函数如下:
其中D1表示直销渠道的需求量,D2表示传统渠道的需求量,?琢表示市场规模,?兹表示消费者对于传统渠道的忠诚程度(0<θ<1),bi表示价格的弹性系数,ti表示交叉价格弹性系数,s表示服务价值,pr是传统渠道的零售价格,pm是直销渠道的价格。和直销渠道相比传统渠道给消费者提供了更好的服务,为保证零售商盈利,用一个严格的凸函数来表示服务价值于成本之间的关系,即c2=,?茁是传统渠道的服务成本系数。
2.1 混沌分岔现象
当系统(6)中其他参数值不变,直销渠道的零售价格调整参数k2=0.009,传统渠道的零售价格调整参数k3=0.004,随传统渠道的批发价格调整参数k1在区间[0.006,0.01]变化时系统出现分岔现象,在[0,0.0066]区间内,系统处于稳定状态,三种价格存在纳什均衡,分别稳定在6.288,15.61,19.02,随着参数k1的变化,决策变量的纳什均衡变得不稳定,在到达0.0066这一时刻,系统发生第一次分岔,制造商制定批发价格时,越重视网络直销价格和传统渠道零售价格,以及批发价格调整速度不断加快的行为,会引起市场进入混沌无序的状态,如图2所示。
当系统中其他参数值不变,传统渠道的批发价格调整参数k1=0.003,传统渠道的零售价格调整参数k3=0.001,随直销渠道的零售价格调整参数k2在区间[0.01,0.014]变化时系统出现分岔现象,在[0,0.0123]区间内,系统处于稳定状态,三种价格存在纳什均衡,分别稳定在(6.51,15.29,18.49),随着参数k2的变化,决策变量的纳什均衡变得不稳定,在到达0.0123这一时刻,系统发生第一次分岔,制造商制定网络直销价格时,越重视批发价格和传统渠道零售价格,以及网络直销价格调整速度不断加快的行为,会引起市场进入混沌无序的状态,如图3所示。
当系统中其他参数值不变,传统渠道的批发价格调整参数k1=0.007,直销渠道的零售价格调整参数k2=0.009,随传统渠道的零售价格调整参数k3在区间[0.0035,0.005]变化时系统出现分岔现象,在[0,0.0047]区间内,系统处于稳定状态,三种价格存在纳什均衡,分别稳定在(6.831,15.61,19.13),随着参数k3的变化,决策变量的纳什均衡变得不稳定,在到达0.0047这一时刻,系统发生分岔,零售商制定传统渠道零售价格时,越重视批发价格和网络直销价格,以及传统渠道零售价格调整速度不断加快的行为,会引起市场进入混沌无序的状态,如图4所示。
2.2 最大Lyapunov指数
最大Lyapunov指数时描述系统动力学特征的方式之一,当最大Lyapunov指数小于0时,系统处于稳定状态,当最大Lyapunov指数大于0时,系统进入混沌状态。下面以k1,k2和k3的变化为例,分析系统的最大Lyapunov指数。当k2=0.009;k3=0.004时,k1在区间[0.006,0.01]变化,最大Lyapunov指数如图5所示。
当k1=0.003;k3=0.001时,k2在区间[0.01,0.014]变化,最大Lyapunov指数如图6所示;
当k1=0.007;k2=0.009;k3在[0.0035,0.005]变化,最大Lyapunov指数如图7所示。
3 混沌控制
當决策参与者的调整系数不断变化并超过一定的合理范围时,整个系统最终会陷入混沌状态,在混沌状态下,会对整个市场经济带来危害,使市场陷入混乱,决策主体的价格和利润的无序波动变得不可预测。此时,决策主体对价格决策的微小变化在后期也在不断变化,中间会产生巨大的差异。可以看出,在混沌状态下,决策主体很难做出正确的决策,而混沌状态是决策机构所不希望看到的。对此采用参数法对系统进行控制。
u是控制系统中的调整参数,当u=0时系统变成原来的离散动力系统即公式(6),所以可以通过调整参数u来对系统进行控制,以避免系统进入混沌状态。从图3可以看出,当决策参与人的调整参数是k1=0.003;k2=0.0145;k3=0.001,制造商决策系统和零售商决策系统处于混沌状态。因此设置与之前相同的参数,加入调节参数u后系统进入稳定状态,图8所示系统控制后的分叉图,图9所示Lyapunov指数。
在制造商和零售商的定价决策中加入调节参数后,系统的混沌得到了有效的消除,产品的批发价格和零售价格从混沌状态重新回到了稳定状态;控制参数u可能由决策者自身决定的,也可能是市场决定的,当决策者意识到市场处于混沌状态时,可以通过多渠道了解最新市场信息,调整自身价格,使市场重回稳定;也可能是当市场处于混沌时,政府制定政策对其进行干预。总而言之,供应链的所有成员都希望自己所处的市场是稳定的,能够在稳定中追求利益的最大化,所以需要供应链系统的所有成员共同携手,对混沌状态采取措施。实验结果表明,调节参数控制是控制系统混沌的一种有效方法,决策者可以将此方法应用于价格决策。
4 结论
本文研究了一个由单一的制造商和零售商组成的考虑利他行为和服务价值的双渠道闭环供应链系统,建立一个动态的博弈模型,运用复杂动力学相关理论进行数据仿真,通过分岔图和最大Lyapunov指数对系统进行混沌特征分析,最后采用调整参数的方法可以对该系统进行了有效控制。得出如下结论:(1)当制造商和零售商的决策是稳定的,并且制造商的决策对零售商的决策有影响时,系统是稳定的。(2)制造商和零售商在一个长动态重复博弈过程中是合理有界的,应采用适当的调节速度,否则整个系统会陷入不稳定状态,对系统造成危害。为了保证系统的稳定性,决策者不能盲目定价。(3)调整参数控制法是控制系统混沌的一种有效方法,制造商和零售商可以将此方法应用于价格决策中。
——————————
参考文献:
〔1〕Yi Tian,Junhai Ma,Lei Xie,Timo Koivum?覿ki,Veikko Sepp?覿nen. Coordination and control of multi-channel supply chain driven by consumers channel preference and sales effort[J]. Chaos, Solitons and Fractals: the interdisciplinary journal of Nonlinear Science, and Nonequilibrium and Complex Phenomena,2020,132.
〔2〕LiuWei Zhao,Jianguo Du,QiWei Wang. Nonlinear analysis and chaos control of the complex dynamics of multi-market Cournot game with bounded rationality[J]. Mathematics and Computers in Simulation,2019,162.
〔3〕Zhanbing Guo,Junhai Ma. Dynamics and implications on a cooperative advertising model in the supply chain[J]. Communications in Nonlinear Science and Numerical Simulation,2018,64.
〔4〕张芳,马小林.双渠道闭环供应链博弈模型的复杂性分析[J].天津工业大学学报,2018,37(03):76-82.
〔5〕马小林,马帅宝,郭玉杰.双渠道闭环供应链博弈模型的动态定价研究[J].哈尔滨商业大学学报(自然科学版),2017,33(02):246-250+256.
〔6〕依不拉音·吾斯曼,郭文强,阿布都热合曼·卡的尔,于凯.专业零售商与厂家直售商的多渠道供应价格博弈的混沌动力学研究[J].运筹与管理,2019,28(11):54-59.
〔7〕Yuehong Guo,Junhai Ma. Research on game model and complexity of retailer collecting and selling in closed-loop supply chain[J]. Applied Mathematical Modelling,2013,37(07).
〔8〕朱晨,张骥骧.考虑零售商双渠道和回收品质量的闭环供应链定价与协调[J/OL].计算机集成制造系统:1-19[2020-05-17].
〔9〕李文龙,王雪,李璐璐,田立平,郑忠义.基于顾客偏好的差别定价回收与契约协调研究[J].生态经济,2020,36(04):62-68.
〔10〕孙浩,王磊,李晨,胡劲松,钟永光,达庆利.回收模式相异的零售商主导型闭环供应链竞争模型研究[J].中国管理科学,2020,28(04):86-98.
〔11〕Dong-Qing Yao,Xiaohang Yue,John Liu. Vertical cost information sharing in a supply chain with value-adding retailers[J]. Omega,2006,36(05).
〔12〕Bin Dan,Guangye Xu,Can Liu. Pricing policies in a dual-channel supply chain with retail services[J]. International Journal of Production Economics,2012,139(01).
〔13〕Yun Chu Chen,Shu-Cherng Fang,Ue-Pyng Wen. Pricing policies for substitutable products in a supply chain with Internet and traditional channels[J]. 2013,224(03).
〔14〕Ruiliang Yan,Zhi Pei. Retail services and firm profit in a dual-channel market[J]. Journal of Retailing and Consumer Services,2009,16(04).
〔15〕王冬冬,劉勇.考虑利他偏好和碳减排努力绩效的供应链决策[J/OL].工业工程与管理:1-15[2020-01-20].
〔16〕Ruguo Fan,Jinchai Lin,Kaiwei Zhu. Study of game models and the complex dynamics of a low-carbon supply chain with an altruistic retailer under consumers low-carbon preference[J]. Physica A: Statistical Mechanics and its Applications,2019,528.
〔17〕王磊,戴更新.利他偏好、服务与供应链Stackelberg博弈研究[J].中国管理科学,2014,22(S1):473-478.
〔18〕Zehui Ge,Zi-Ke Zhang,Linyuan Lü,Tao Zhou,Ning Xi. How altruism works: An evolutionary model of supply networks[J]. Physica A: Statistical Mechanics and its Applications,2012,391(03).
〔19〕曾婷婷,李登峰,郑小雪.考虑互惠偏好的闭环供应链系统合作机制研究[J].系统科学与数学,2020,40(01):41-62.
〔20〕黄祖庆,蒋连杰,孟丽君.供应链竞争下考虑消费者偏好的最优决策机制研究[J/OL].工业工程与管理:1-10[2020-05-17].
〔21〕兰龙辉,郑小雪,李登峰,曾婷婷.考虑互惠偏好的闭环供应链合作博弈模型[J/OL].计算机集成制造系统:1-22[2020-05-17].
〔22〕徐静,程发新,刘吉林.政府补贴下考虑消费者低碳偏好的闭环供应链网络均衡决策[J].科技管理研究,2019,39(13):266-274.
〔23〕孙玉玲,袁晓杰,石岿然.基于利他偏好的鲜活农产品供应链决策研究[J].系统工程理论与实践,2017,37(05):1243-1253.
〔24〕Praveen K. Kopalle, Ambar G. Rao, Jo?觔o L. Assun?觭?觔o. Asymmetric Reference Price Effects and Dynamic Pricing Policies. 1996, 15(01):60-85.
