应用混合遗传算法的多集货中心多车型整车路径规划研究

刘建胜，谭文越

（南昌大学机电工程学院，江西 南昌 330031）

1 引言

随着汽车工业的发展，第三方整车物流（FVL）已成为汽车企业成品车物流的趋势。作为第三利润源泉，整车物流变得原来越重要，而配送方案的优化则是降低物流成本的根本保证。

VRP 最早由文献[1]于1959 年首次提出。根据研究的重点不同，VRP 有多种分类方式。如按特征分类，有装货问题、卸货问题和装卸混合问题；按车辆载货情况分类，有满载和非满载问题[2]；按车场数目分类，有单车场[3]和多车场问题[4-5]；按运输车类型、商品车类型分类，有单车型[6]和多车型[7]问题等等。由于情况的不同，车辆路径问题的模型构造及算法会有很大差别。

VRP 属于NP-hard 问题，在规模较大时很难求出精确解。其求解算法大体上可以分为精确算法、启发式算法和智能优化算法三大类。用于求解VRP 问题的启发式算法有禁忌搜索、模拟退火、遗传算法[8]、粒子群算法[9]、蚁群算法[10]等。每一种算法都有其优势，但是单独工作都会存在一些缺陷；因此近些年的研究开始侧重于构造混合算法来解决实际问题。

综上所述，与传统的VRP 问题不同，着重研究具有多专业集货中心、多种轿运车型、多种运输车型，并考虑路线成本权重不同和配载几何约束的整车运输车辆路径规划问题。同时设计出一种基于遗传算法与粒子群算法的改进混合遗传算法，并通过实例仿真证实了该算法的高效性与收敛性。

2 整车批次运输优化模型

2.1 问题描述

某汽车厂商的产业模式是集团公司多专业集货中心式。其在一个城市具有多个集货中心，每一个集货中心具有相同规格系列的商品车型。而某一物流公司在全国各地有若干个轿运车车场，车场内有多种轿运车型，每种轿运车型具有不同的载重量和规格，且一般规格大的轿运车每单位公里的运输成本也会相对较高。此时汽车厂商接到一批订单，客户需要一批不同规格的商品车。物流公司接到汽车厂商的运单后，根据客户需求及实际情况，选择一定数量相应规格的轿运车进行配载，并制定每辆轿运车的路径规划方案。方案制定后，如图1 所示。轿运车场派出若干辆轿运车，每辆轿运车都要按所分配任务前往各集货中心装载所需类型的商品车，然后运输至各个客户点，完成运输任务的轿运车回到公司的另一个轿运车场等待下一次运输任务。

图1 路径示意图Fig.1 Path Diagram

2.2 数学模型

2.2.1 模型假设

（1）考虑到集货中心和客户点规模对运输和装卸货成本的影响，将各中心和客户地简化为点。

（2）每个集货中心只有一种商品车，且数量足够多。

（3）每个客户点的订单都是小批量，均只由一辆轿运车一次性满足，一辆轿运车可以完成多个客户点的配送任务；

（4）运输处于理想状态，不考虑自然因素带来的风险和损失。

2.2.2 模型建立

根据以上假设，建立多集货中心多车型整车物流模型，目标函数为：

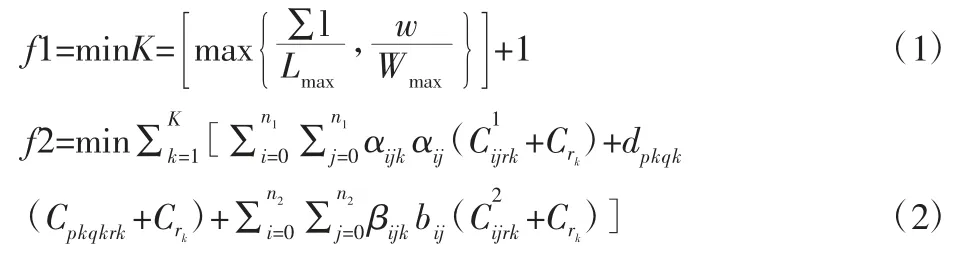
约束条件为：

式中：Σl、Σw—商品车的总车身长和总车身重；Lmax、Wmax—容量最大类型的轿运车所能装载的最大车身长和车重；n1—集货中心数量；n2—客户点数量；rk—第k 辆轿运车的车型；ki—车型为 i 的轿运车数量；wi、li—车型为 i 的商品车的重量与车身长；K—轿运车的总数；aij—集货中心i 到j 的距离；bij—客户点 i 到 j 的距离—第 k 辆轿运车最后一个到达的集货点pk与第一个到达的客户点qk的距离—对车型为rk的轿运车来说，从集货中心i 到j 和从客户点i 到j 的单位距离路费—对车型为rk的轿运车来说最后一个到达的集货点pk与第一个到达的客户点qk的单位距离路费—车型为rk的轿运车的单位距离油费、限载重量、限载总长度；Sik—第k 辆轿运车在集货中心i 装载的车型为i 的商品车数量；Dij—客户点i 对商品车型j 的需求量。

式（1）和式（2）为目标函数，分别表示轿运车数量最小，物流总成本最低；式（3）、式（4）、式（8）为（0～1）变量；式（5）表示集货中心流量守恒；式（6）表示轿运车数量之和；式（7）表示轿运车的载重限制；式（8）表示轿运车的装载车长限制；式（10）表示每个客户点有且仅有一辆轿运车负责配送；式（11）和式（12）表示客户点流量守恒；式（13）表示供应与需求平衡。

3 混合遗传算法设计

遗传算法作为一种启发式搜索算法，在处理不连续、不可微和非凸等问题上可以取得很好的效果，并且其具有良好的全局搜索能力，可以快速搜索解空间的全局解，而不会陷入局部最优解的快速下降陷阱。遗传算法不依赖于问题的具体领域，具有很强的鲁棒性，因此被广泛用来解决各种复杂的优化问题。但遗传算法也存在明显的缺点，如收敛速度慢，局部搜索能力差，控制变量多等。粒子群算法（PSO）由文献[11]提出。与遗传算法类似，PSO 是一种迭代优化算法。与遗传算法相比，标准PSO 具有较少的控制变量。它遵循个体极值和全局极值进行极值优化，易于操作和快速收敛。然而，随着迭代次数的增加，人口收敛时，粒子越来越相似，易于陷入局部最优解。为解决以上问题，提出一种混合算法GA-PSO，该算法结合了遗传算法的全局优化型和粒子群算法的快速局部搜索性能。不同于传统粒子群算法中通过单纯的跟踪极值来更新粒子位置，而是引入遗传算法中的交叉和变异操作，通过染色体与个体极值和群体极值的交叉和自身变异的方式来搜索最优解。算法步骤如下：

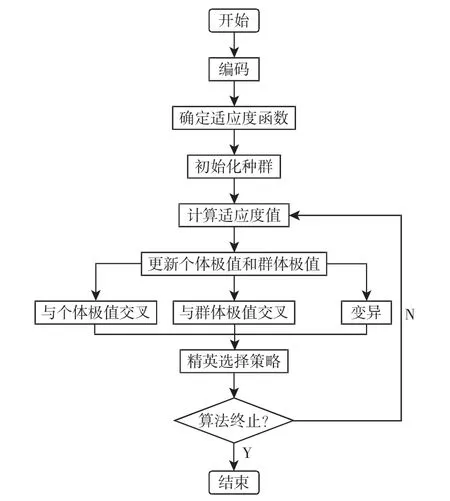
图2 算法流程图Fig.2 Program Flow Diagram

3.1 染色体编码

采用自然数编码，编码中的数组需要包含三个信息：集货中心点、客户点和轿运车型号，这样才能确定一辆轿运车的路线方案。比如，比如：-3-1-2-6-4 16 10 M+1。这组数字表示车型为1的轿运车从起始车场出发，先依次去集货中心3、1、2、6 处装载商品车，然后依次运至客户点16、10 处完成配送任务，最后回到终点车场。集货中心序号前加负号是为了区分集货中心和客户点，M 代表一个绝对值很大的负数，一是为了区别于客户点的数字，二是为了与下辆车的路线分割开来，且由于M 很小，所以很容易就能从数组中找到各个分割点；如果把上面的这串数字看成一组，那么代表一个可行解的染色体编码就是由若干个组连接而成，一个组对应一辆轿运车的运输路线，有几个组就代表了该方案总共用了几辆轿运车，很容易从编码中得到我们所要的信息。

3.2 适应度函数

遗传算法使用适应度函数值来评估个体并指导搜索，因此适应度函数值的选择非常重要，选择不当容易导致欺骗问题。其选择标准是：规范性（单值、连续、严格单调），合理性（计算量小）和具有普遍性。因此使用谢菲尔德遗传算法工具箱中的“ranking（）”函数来获取适应度。经过这样处理后，成本较低的个体具有较大的适应度值，并且群体的适应度函数值将在区间（0，2）中分布更均匀。

式中：Nind—种群中个体的数量。每个个体的适应度值根据它在排序种群中的位置Pos 计算出来；sp—指定压差。

该算法首先对目标函数值进行降序排序。最小适应度个体被放置在排序的目标函数值列表的第一个位置。

3.3 种群初始化

要生成一定规模的种群，并且同时满足所有的约束，应该先生成客户点，然后才能对应生成集货中心点和确定商品车需求量，具体生成有以下几个步骤：

（1）先随意生成一个1～20 的乱序数组

（2）选择轿运车车型，这里使用一个选择结构：

u=rand；if0＜u&u≤pau=1；

else if pa＜u&u≤pbu=2；

else u=3；

为了达到轿运车数量最小的目标，应尽可能选择容量大的轿运车。而车型1 的容量最大，其次是车型2，因此参数pa 和pb应根据每种轿运车的运载能力来确定。

（3）将这个数组分隔开来。只要装载重量或者长度超出轿运车的限制，就插入一趋于负无穷的数；

（4）根据客户的需求确定集货中心点，然后生成一个无序数组，并在取相反的数字后将其插入到客户点前面。

（5）重复步骤（2）～（4），直至所有的客户点都分配好轿运车。

3.4 更新染色体（粒子）

在每次迭代中更新个体极值和群体极值。

3.5 交叉操作

个体通过和个体极值和群体极值交叉来更新，交叉方法采用整数交叉法。首先删除染色体中所插入的负数只留下代表客户点的20 位数。然后随机选择两个交叉位置，把个体和个体极值或者群体极值进行交叉。为避免重复编码，交换前应删除重复点，例如：

A=1 7 3［10 15 8 9］16 13 11 2 17 19 20 4 5 6 12 18 14

B=7 9 1［12 2 20 16］19 5 6 3 15 13 18 11 14 4 8 10 17

首先从A 染色体中去除重复的数字12，2，20，16 然后从B染色体中去除 10，15，8，9，然后我们得到：

A=1 7 3［10 15 8 9］13 11 17 19 4 5 6 18 14

B=7 1［12 2 20 16］19 5 6 3 13 18 11 14 4 17

接下来，将交换的染色体片段分别移到染色体最前端，可以得到：

A=12 2 20 16 1 7 3 10 15 8 9 13 11 17 19 4 5 6 18 14

B=10 15 8 9 7 1 12 2 20 16 19 5 6 3 13 18 11 14 4 17

然后我们重复初始化操作，插入表示运输车辆的集货中心和车型的数字，从而生成一对新的染色体。

3.6 变异操作

遗传算法常用的变异操作有基本位变异、均匀变异和高斯变异等。变异操作可以有效避免过早收敛，保持种群的多样性。使用的多点变异属于基本位变异的一种。具体操作如下：首先在种群中随机选择三个基因位点14、10、18，然后将三个基因位点之间的两个染色体片段互换。例如：

P=13 17 16 4 15 8 2［14］11 1［10］6 7 3 20［18］9 5 12

变异后得到：

P′=13 17 16 4 15 8 2［6］7 3 20 18［14］11 1［10］9 5 12

3.7 精英选择

我们按照染色体适应度值从大至小进行排序。我们将每代中具有最大适应度值的个体定义为精英个体，在通过交叉和变异操作产生的种群中，具有较高适应度值的个体被选择并复制两次传给下一代，排在末位的个体则被舍弃。在迭代中，使用这种自适应方法不仅可以有效的避免早熟和近亲繁殖，还可以加快种群整体收敛速度。公式如下：

式中：m（i）—第 i 条染色体的适应度值；num—种群大小；N（i）—复制的第i 条染色体复制的次数。

4 算例仿真及结果分析

4.1 算例仿真

设某物流公司有三种轿运车车型，车型规格，如表1 所示。各集货中心坐标和成品车的规格，如表2 所示。各客户的坐标和订单，如表3 所示。本算例含有7 个集货中心和20 个客户点。

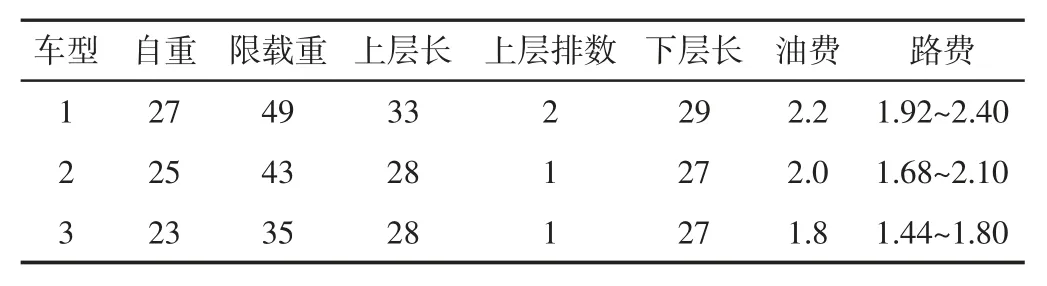
表1 轿运车规格Tab.1 Relevant Data of Transport Vehicles

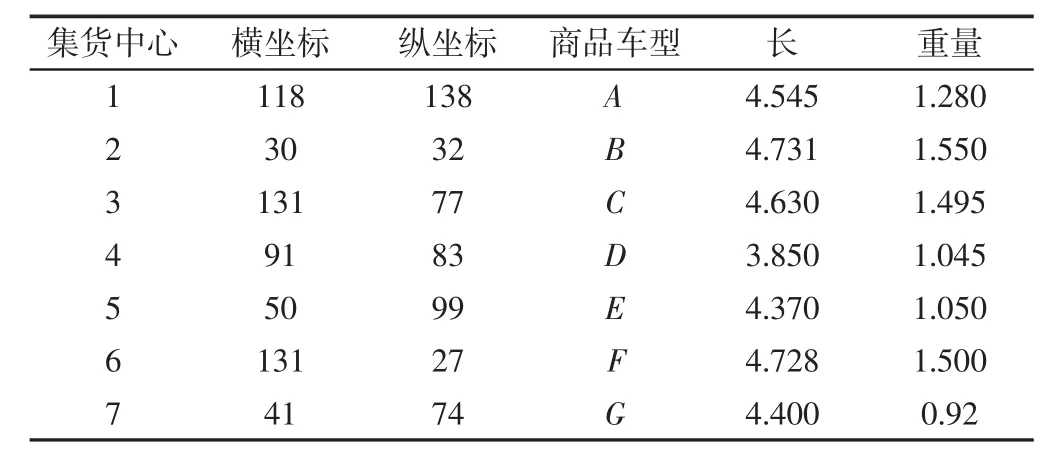
表2 集货中心位置和商品车规格Tab.2 The Information of Depot and Finished Vehicles

表3 各客户点位置需求Tab.3 The Demand of Each Customer Point

优化目标是最小化运输成本。运输成本由路费和油费两部分构成。每单位距离的油费与轿运车型号有关，而路费不仅取决于轿运车车型还取决于具体的运输路线。

用Matlab2015b 针对算例进行编程，并在一台Intel3.7GHz，4GRAM 的电脑上进行运行实验，设定迭代次数为1000。从实验结果中可以看出：总的运输费用为20824.363 元，所需轿运车数量为8 辆。路由方案，如图3 所示。详细的路由及运载方案如表4，算法迭代图，如图4 所示。

图3 路径优化方案Fig.3 The Routing Solution

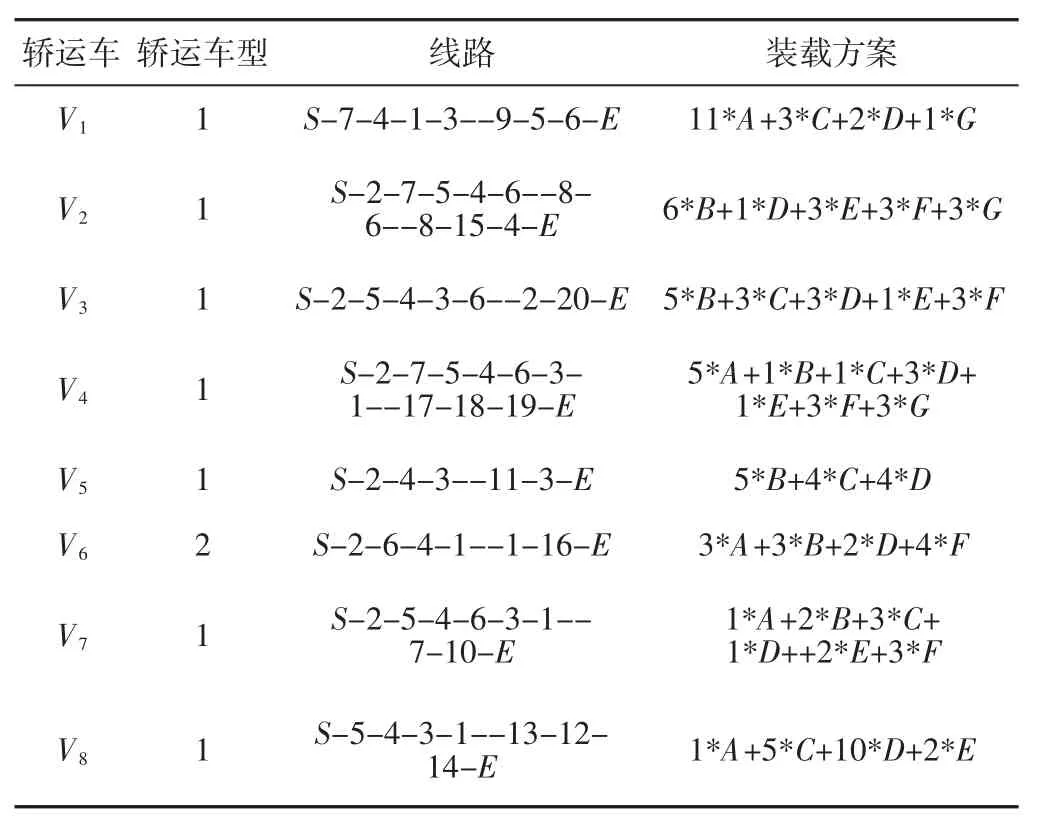
表4 轿运车线路与配载明细Tab.4 Route and Loading Details

4.2 实验结果分析和算法对比

为了验证GA-PSO 算法有效性，将GA-PSO 与GA 分别进算了十次。在两种算法中采用了相同的编码，初始种群大小设定为100，遗传算法中，交叉概率设定为0.8，变异概率设定为0.05。两种算法的最优解迭代图，如图4、图5 所示。实验最优解在GAPSO 的341 代中得到。两种算法的对比结果，举出了每次试验中的各算法最差值和平均值，如表5 所示。通过比较两种算法，GAPSO 收敛速度更快，优化结果更好。最重要的是GA-PSO 的运行时间只是GA 的5%左右。实验表明，我们提出的GA-PSO 算法具有更好的性能，可以快速的找到最优解或者近似最优解。为了充分验证此算法的有效性与效率，进行了多次实验。在下面这些测试案例中，模型和假设不变，测试算例的位置坐标仍然是随机生成。随着算例规模的增加（集货中心数量和订单数量），两种算法的运行时间差异愈发明显，如表6 所示。

图4 混合算法迭代图Fig.4 Optimization Iteration Figure of GA-PSO

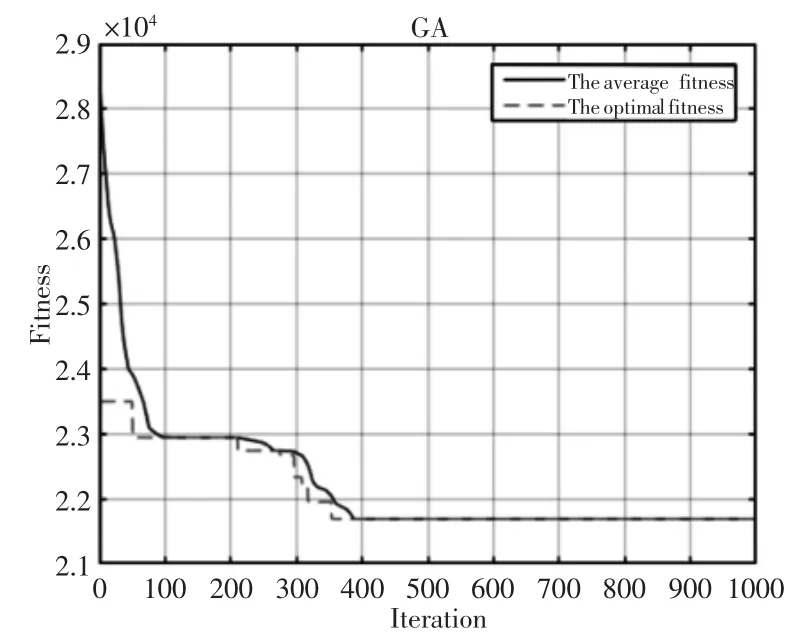
图5 遗传算法迭代图Fig.5 Optimization Iteration Figure of GA

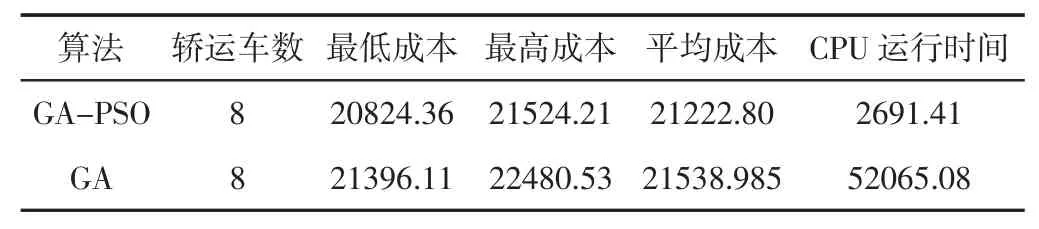
表5 算法结果比较Tab.5 Two Algorithm Comparison

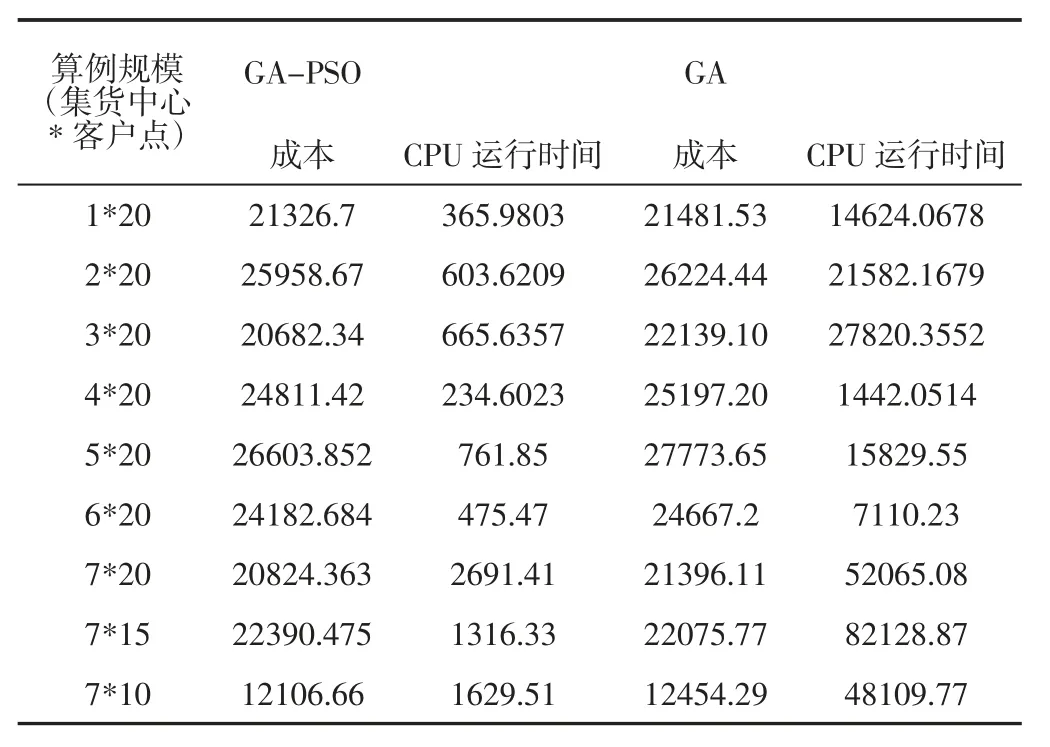
表6 测试算例算法性能对比Tab.6 Algorithm Comparison of Test Cases

5 结论

结合整车物流中的实际运输情况，综合考虑了物流成本和物流公司人力成本等要求，针对多集货中心、多轿运车型、多商品车型的整车物流运输问题，建立了以物流总成本最低和车辆数最小为目标的（0～1）整数规划模型，包括运输的路费成本、油费成本等，并设计出一种基于遗传和粒子群算法的算法GA-PSO 进行求解，解决了此整车物流配送中的路径优化问题，并进行了实例验证并将结果与遗传算法实验结果进行对比，结果说明此模型和算法具有可行性和实用性。