基于工图图像的法兰三维重建方法研究

于 灏 ，杨建鸣 ，王小刚 ，2

（1.内蒙古科技大学机械工程学院，内蒙古 包头 014010；2 包头钢铁钢联股份有限公司焦化厂，内蒙古 包头 014010）

1 引言

随着机械、汽车等领域的快速发展为了减少繁重工作量，对CAD 系统提出了更高的要求，实现从工程图纸向三位实体的快速转化可以有效提高设计效率、缩短开发周期与降低前期投资成本[1]。工程图纸三视图重建三维模型的课题在上世纪70 年代被文献[2-4]提出后便得到了普遍关注与深入研究。文献[5]提出提出了一种人机交互识别算法，算法通过人工选取基本环并补充视图中缺失线条，可以有效的实现基元体的完整提取；文献[6]依据三视图轮廓生成原始三维形体然后再依据工图中信息对初始形体进行切削最终得到目标模型；文献[7]基于Shum 与Soni 算法提出一种启发式线索算法，在三维重建中对于相贯体旋转半轮廓恢复有较好效果，但其仅可以处理旋转轴与坐标轴相平行的二次曲面；文献[8]以可信度为引导提出了一种交互式基元体验证算法，可处理基元体信息缺失的基本视图与剖视图；文献[9]提出了基于面域理解的三维重建算法，算法依据投影规则建立实体面进而获得零件的边界模型；文献[10]对二次曲面体重建进行了研究，算法利用多点构造的三维二次曲线生成线框模型，分别采用最小内角法与决策链法生成候选曲面与消除假元；文献[11]提出了基于共轭直径的一种新算法，直接在线框模型中生成面环省略了候选步骤，但是算法不适合处理二维曲面相交与相贯的三维重建。

三维重建研究已经取得了丰硕成果但是由于研究存在一定的局限性，要应用于实际还需要更近一步的研究。大多数二维向三维的转化研究是基于dxf 或dwg 格式文件的，但是需要转化的常常是以纸质形式保存的图纸，这一点大大限制了二维转三维的实际意义与用途；大多数的二维向三维转化所需条件苛刻且需要专门的平台或系统这大大限制了二维转三维的实际应用与推广；由于二维转三维提出较早且近期科研人员关注不多，所以对于新方法与新技术的应用不多。以纸质图纸为研究对象，以Matlab 与SolidWorks 为平台并结合数字图像处理与神经网络等技术，提出了一种基于工图图像的法兰零件重建方法，有效的弥补了上述不足。

2 方法简述与理论基础

2.1 方法简述

针对法兰零件的三维重建提出了一种较为有效的方法，首先对工程图纸进行预处理，预处理包括对纸质工程图纸的扫描、对光栅图像的灰度化、对灰度图像的降噪、灰度图像分割以及二值图像细化。然后采用Harris 角点识别算识别工图中角点，采用Hough 检测算法检测工图中的圆，采用BP 神经网络以及图像特征建立参数预测模型。最后依据模型预测参数应用SolidWorks参数化建模功能实现法兰零件的三维重建。

2.2 Harris 角点检测原理

Harris 基本原理是采用检测窗口在被检测的图像上滑动，当其在某点任意滑动时，且其在任意方向滑动的灰度值变化较大则称这一点为角点。窗口函数滑动一定偏移量后其灰度的变化可以用 E（u，v）表示，其值可以用式（1）求得：

式中：E（u，v）—图像灰度偏差；W（x，y）—窗口函数；I（x，y）—被检测图像；Ix图像在x 方向梯度；Iy图像在y 方向梯度。当图像灰度偏差取常数时，这一函数可以用椭圆来描述，其特征值可以用以判断角点是否存在。

2.3 Hough 圆检测原理

Hough 变换的基本原理是把图像所在空间中圆的边界点映射到Hough 变换空间，如图1 所示。在图像空间中的点被映射到参数空间后是一个圆，图1（a）是原图像空间的圆以及圆上的点，图1（b）是点映射到Hough 变换空间后所形成的圆，其中众多圆的交点是被检测到的圆的圆心，而这些圆的半径则是被检测到圆的半径，所以合理设定角度步长、半径步长以及要检测圆的半径的极限值对Hough 检测十分重要。

2.4 BP 神经网络

反向传播神经网络（back propagation，BP）是一种按照误差逆向传播算法训练的多层前馈神经网络，目前应用较为广泛。BP神经网络神经元的激活函数可以由式（3）描述：

式中：neti—神经元i 的结果；wij—前一层网络传递到神经元i 的权值；xi—输入值；θ—误差值。BP 神经网络的训练思路是要求误差函数减小最快即沿梯度方向，其迭代方程，如式（4）所示。

式中：xk+1—迭代计算后的偏差与权值；xk—在进行迭代计算前的偏差与权值；ak—BP 网络训练时的学习率；gk—误差函数梯度。

采用标准差计算BP 神经网络的误差，前向传播计算如式（5）所示。输出，如式（6）所示。其中误差定义，如式（7）所示。

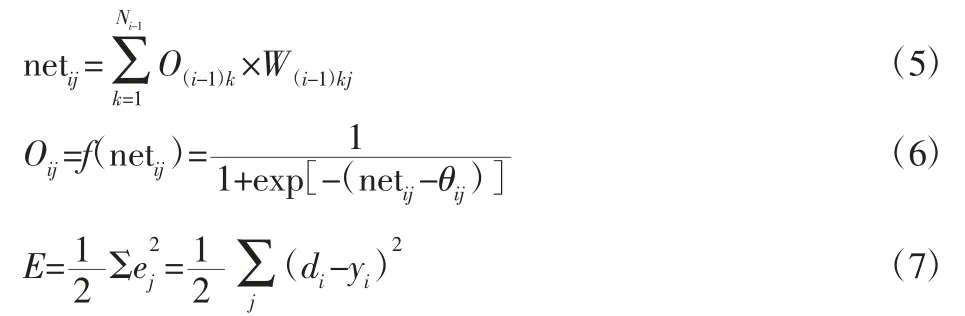
式中：netij—网络计算值；O（i-1）k—前一层输出；W（i-1）kj—权值；Oij—输出结果；θij—误差；E—均方误差；di—预测结果；yi—实际结果。

图1 原空间与Hough 变换空间Fig.1 Original Space and Hough Transform Space

3 实验及结果分析

所做实验采用的是windows 系统，处理器为Interl（R）Core（TM）CPU @ 2.40GHZ，内存（RAM）为 8.00GB，系统类型为 64位，所用软件为MATLAB 2014a。工程图纸预处理后首先对其进行角点检测与圆检测，角点检测过程中先提取x 与y 方向分量然后依据Harris 原理提取角点，如图2 所示。由图可知本方法可有效提取工程图中的角点。圆检测过程中首先进行边缘检测，然后将原有图像映射到Hough 变换空间；对局部交点个数进行统计，得到其最大值并记录其坐标。如图3 所示，其中，边缘检测结果，如图3（a）所示。Hough 检测结果，如图3（b）所示。处理图像的原图，如图3（c）所示。被检测的到的圆标记后图，如图3（d）所示。

图2 Harris 角点检测Fig.2 Harris Corner Detection

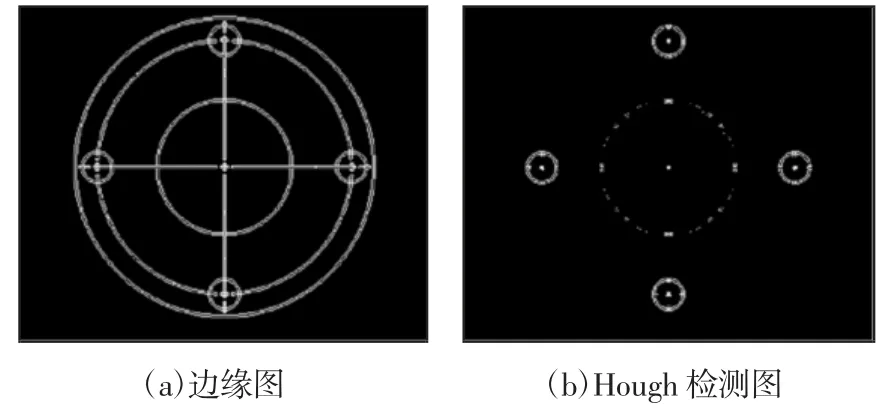
图3 Hough 圆检测图Fig.3 Hough Circle Detection Chart

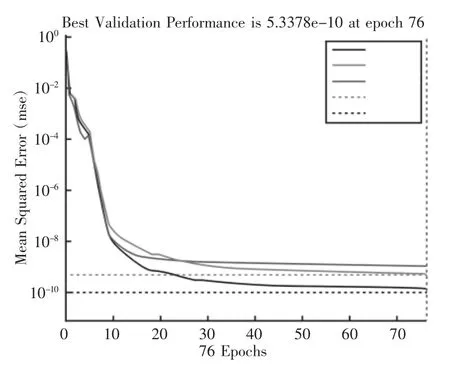
图4 高度识别均方误差Fig.4 Height Recognition Mean Square Error

将角点与圆等特征信息输入到BP 神经网络，BP 神经网络经学习后即可得到相应模型，用以识别法兰零件的参数。一个简单的法兰零件至少需要用大圆直径、大圆高度、小圆直径、小圆高度中心孔直径、倒角尺寸、阵列个数与小孔直径等参数描述，以大圆高度为例简述识别过程。

实验数据共50 组数据其中30 组作为训练数据，20 组作为测试数据。神经网络在识别法兰盘大圆盘高度训练过程中的均方误差，如图4 所示。从图中可以看出均方误差在经过76 次迭代后达到设定目标，最佳测试结果其误差约为5.34e-10。BP 神经网络的预测值域真实值的比较图，如图5 所示。从图中可以看出神经网络的预测结果与真实值基本重合，取得了较好效果其误差十分微小，预测结果与真实值之间的标准差，如图6 所示。BP 预测结果、真实值与标准差表，如表1 所示。同理可以得到其他法兰零件的相关参数，对识别后的参数进行取整其结果，如图7 所示，把这一结果导入到SolidWorks 的零件设计表中据此自动生成法兰零件的三维模，如图8 所示。法兰零件的工程图纸扫描图像，如图9所示。

图5 高度预测结果Fig.5 Height Prediction Results

图6 高度标准差Fig.6 High Standard Deviation

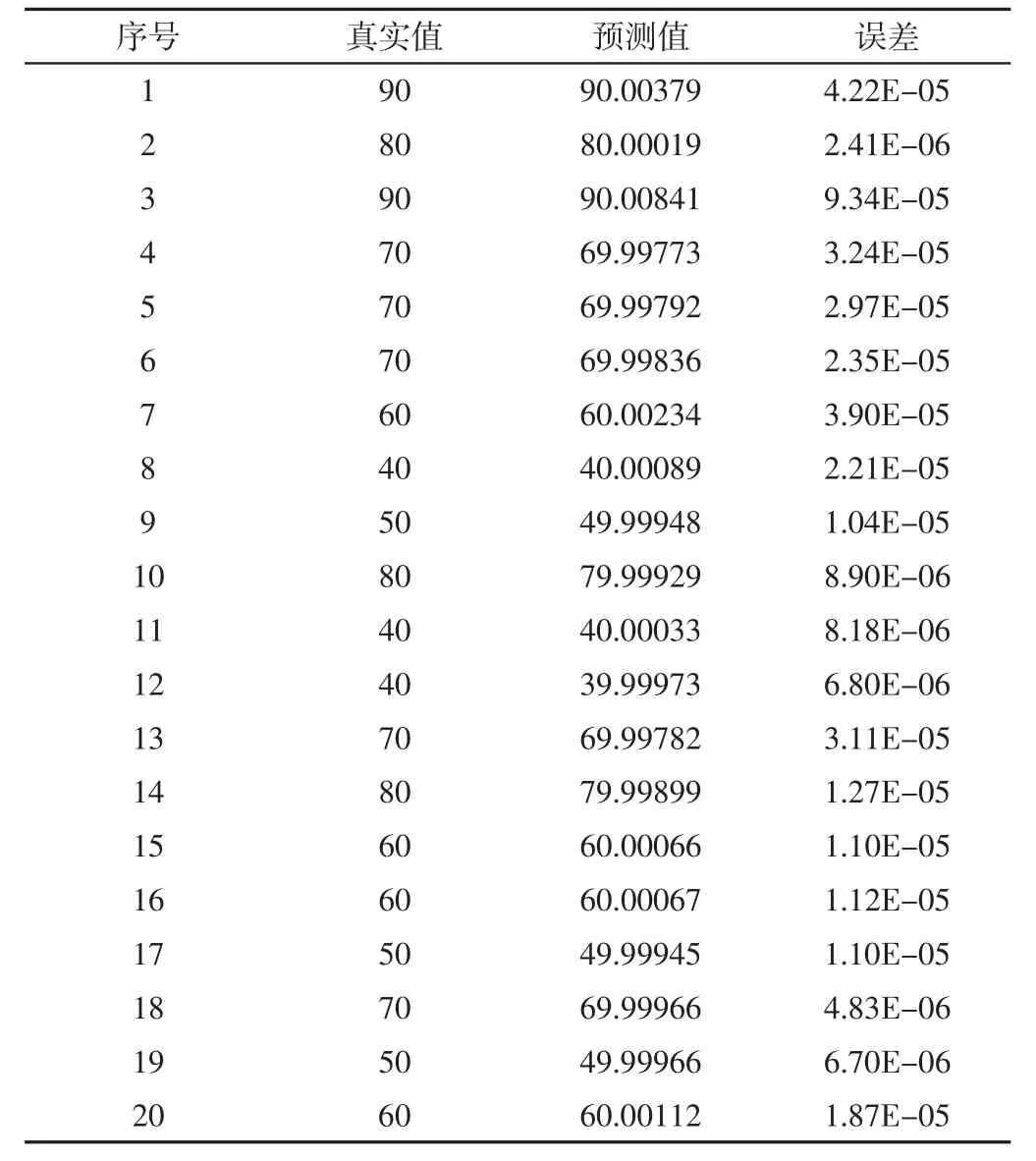
表1 BP 高度预测结果Tab.1 BP Height Prediction Results

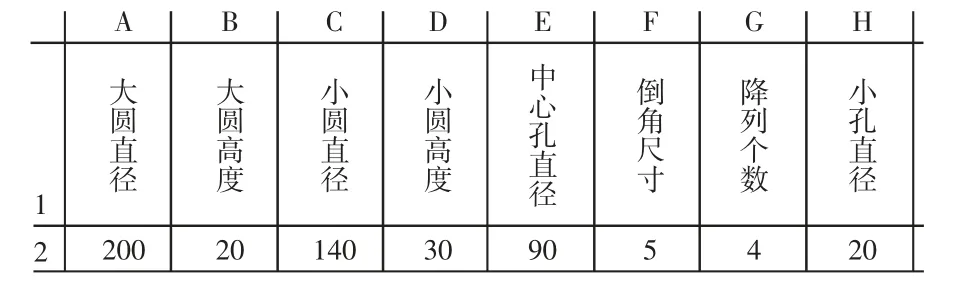
图7 BP 网络计算参数Fig.7 BP Network Computing Parameters

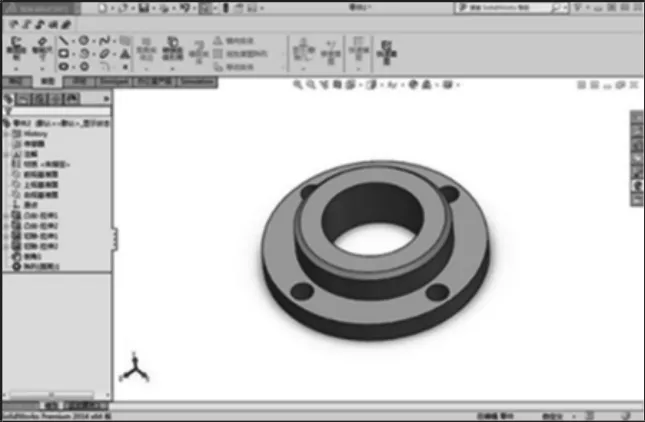
图8 重建法兰模型Fig.8 Reconstruction of Flange Model

图9 法兰零件工程图Fig.9 Flanged Parts Engineering Drawings

4 结语

提出了一种基于工图图像的法兰三维重建方法，采用了图像处理、特征提取与BP 神经网络等技术，一定程度上提高了重建效率与精度；方法以纸质图纸为研究对象一定程度上拓宽了三维重建的实际应用范围；方法以Matlab 与SolidWorks 为平台不需要设计专门的系统或平台，有利于二维转三维的实现与推广。实验证明本方法可有效且快速的重建法兰零件三维模型，为工程图纸的三维重建提供了新思路与方法，对后续研究有一定的指导意义。