适应增材制造构件倾角约束的拓扑优化方法

2020-11-23杜义贤田启华

机械设计与制造 2020年11期

杜义贤，徐明，周鹏，田启华

（1.三峡大学机械与动力学院，湖北宜昌 443002；2.水电机械设备设计与维护湖北省重点实验室，湖北宜昌 443002）

1 引言

与传统的制造技术相比，增材制造技术（AdditiveManufacture，AM）通过材料层层累加的方式实现结构的制备，极大地拓宽了设计空间，与拓扑优化的完美融合，使得几何构型的复杂程度不再是工程设计考虑的主要指标[1]。然而，现阶段普遍遇到的难题是结构的倾角（与基面相对的边界和基面所成的夹角）小于临界值[2-4]时无法直接打印出来。目前解决的办法主要是添加附加支撑[5-6]，但是附加支撑会增加打印的时间和材料，导致成本的增加。文献[7]搜索最优的打印方向，降低所使用支撑结构的总体积；文献[8-9]固定打印方向，优化模型的形状使边界面向基底的面积减小，从而减少支撑结构；文献[10]将支撑结构融合为初始模型的一部分形成自支撑，然后对附加支撑结构进行优化，达到减少支撑的目的。上述研究主要考虑的是减少支撑，不能消除附加支撑带来的影响。基于文献[11]提出的AM 过滤方法，构建一种新的单元密度更新迭代规则，与拓扑优化程序[12]相结合，以MBB 梁和悬臂梁为例，定义不同的基底方向，拓扑出可直接打印的构型。为了更直观验证所提出的单元密度更新迭代规则的可行性，将MBB 梁W方向和悬臂梁的S方向的构型进行模型重构，并测量典型倾角的大小。

2 建立单元密度更新迭代规则

将矩形设计域均匀离散为ni×nj个正方形单元，i 方向为打印方向。每个单元的可打印密度 ξ（i，j）取决于初始密度 x（i，j），其中i 和j 分别表示单元的竖直位置和水平位置，第一层位于基底上，其层索引序号为i=1。根据增材制造技术层积堆叠制造原理，新增层只有被已打印层充分支撑才可打印，定义所有依靠基底层（i=1）支撑的单元都可打印。结构的倾角在［45°，90°］可直接打印[2-4]，Martthijs 提出单元的可打印密度与该位置的初始密度及其下一层的可打印密度有关，得到的角度约束为45°，但是在实际打印过程中发现拓扑出来的结构会出现坍塌。若单元的可打印密度由该位置的初始密度及其下多层的可打印密度决定，得到的角度约束会随着决定层数的增多而增大，打印的结构稳定性也会越好，但是角度约束越大拓扑构型的多样性就越少。因此为了实现可直接打印且结构尽可能的多样，规定每个单元的可打印密度ξ（i，j）既与位置（i，j）处的初始密度 x（i，j）和其下一层即 i-1 的可打印密度相关，同时也与位置（i，j）下面第二层即i-2 层的可打印密度相关。

设（i，j）处初始密度为 x（i，j），（i，j）处可打印密度为 ξ（i，j），位于（i，j）处单元正下方i-1 层与i-2 层及左右相邻的单元共6 个单元组成支撑区域 S（i，j），如图 1 所示。S（i，j）中位于 i-1 层的三个单元最大可打印密度为 Ξ（i，j），S（i，j）中位于 i-2 层的三个单元最大可打印密度为 Ξ（i-1，j），显然若 i=2 则 Ξ（i-1，j）=0。建立如下单元密度更新迭代规则：规定（i，j）处可打印密度 ξ（i，j）为相应支撑区域内i-1 层最大可打印密度和i-2 层最大可打印密度以及该处初始密度的最小值。

由此建立更新迭代模型公式化如下：

式中：ξ（i，j）—每次迭代后单元（i，j）处的可打印密度；x（i，j）—每次迭代前单元（i，j）处的初始密度—与单元（i，j）相应的支撑区域内i-1 层与i-2 层最大可打印密度的较小值；下一行临近三个单元可打印密度最大值。

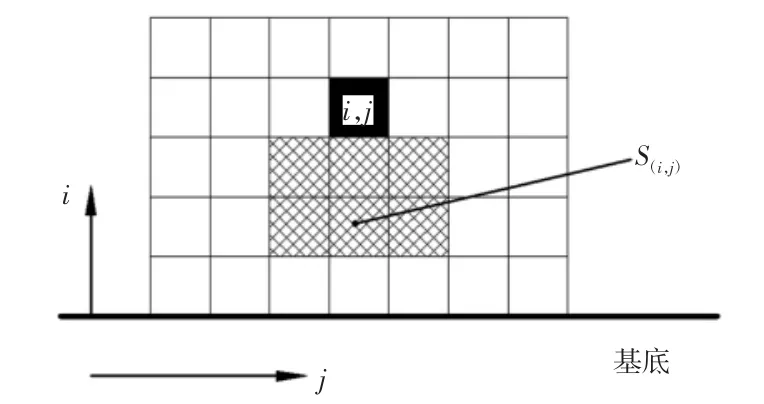
图1 单元（i，j）及其支撑区域 S（i，j）Fig.1 Definition Supporting Region S（i，j） for Element（i，j）

迭代的过程示例，如图2 所示。按照迭代规则对每一层的可打印密度进行更新，最终得到密度分布图，如图2（l）所示。用一条线段将有材料区域和空白区域分隔开来，即可在宏观上得到一条与基面夹角为arctan2（约为63°）的清晰结构边界，如图2（l）所示。

图2 逐层迭代过程Fig.2 Conceptual Layer-by-Layer Iterative Process

为了便于进行敏度分析，将迭代模型用光滑近似的可微形式进行表示，定义如下近似形式：

所以单元密度迭代的模型可以表示为：

由式（8）、式（9）和式（10）知第 i 层的可打印密度与第 1 层到第i-1 层的可打印密度均密切相关，为了在敏度分析中求解更高效，采用伴随公式表达可打印密度与初始密度的关系：

式中：S′—smin 符号的简写形式，单一下标为层数索引符号。

3 拓扑优化数学模型及敏度分析

3.1 拓扑优化数学模型

基于SIMP[15]的结构拓扑优化技术，在满足约束条件下，以可打印结构的柔度c 对最小为目标。根据前文分析可知，目标函数取决于可打印结构密度矩阵ξ（x），而可打印结构密度矩阵ξ（x）又取决于初始密度x，建立的优化问题的数学模型如下：

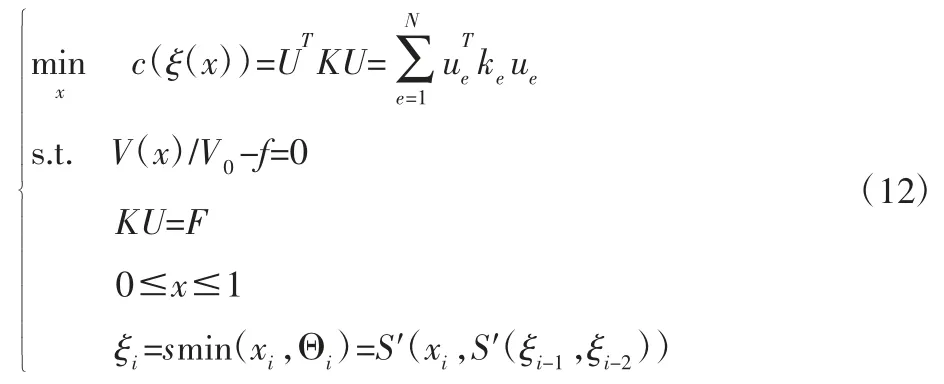
式中：c—结构整体的柔度；KU=F—结构力学控制方程；V（x）—优化后结构的体积；V0—设计域体积；f—体积系数，ξi单元密度迭代规则即倾角约束。

3.2 目标函数的敏度分析

在式（12）的拓扑优化模型中，目标函数c 关于设计变量x的敏度为：

在矿区内针对性采集了石墨矿、斜长角闪片岩、大理岩、黑云斜长石英片岩、黑云斜长片麻岩、黑云花岗闪长岩、石英闪长岩等350件物性标本，进行了电性测定，统计结果见表2。

式中：λi—乘子矢量，对于第一层和第二层有≡式（14）微分形式为：

式中：δij—克罗内克函数，当 i=j 时 δij=1，当 i≠j 时 δij=0 且 1≤j≤ni。由于可打印密度只取决于其下层的初始密度，所以当i＜j时所以可以去掉式（15）中 i＜j 的项。提取求和公式中 i=j 的项，利用整理式（15）得到：

由于每个乘子都取决于其上面两层相关联的乘子，因此评估的顺序将从顶层开始向下进行，与瞬态问题伴随灵敏度分析相似[14]，可得：

式中各微分形式均可根据式（4）～式（10）得到。

所以，目标函数关于初始密度的敏度为：

3.3 模型求解

根据所建立的优化模型，结合单元密度更新迭代规则，采用OC 算法（优化准则）对模型进行优化求解，优化步骤如下：

（1）定义设计初始条件即设计域、载荷条件、约束条件等边界条件及材料相关属性，将材料均匀的离散到每个单元，得到初始密度分布；

（2）按式（11）进行单元密度的更新迭代得到满足倾角约束的可打印密度分布；

（3）进行有限元分析求解获取结构整体位移场U；

（4）按式（12）和式（21）计算得到目标函数的值和关于设计变量的敏度分析计算；

（5）采用OC 算法更新设计变量，得到新的密度分布；

（6）根据收敛条件判断目标函数是否收敛，若收敛，则输出拓扑优化结构，否则转到（2）。

4 数值算例分析

以MBB 梁和悬臂梁（纵横比均为3）为例，将单元密度的更新迭代规则与拓扑优化程序相结合，迭代的初始值分别设定为P=40，ξ0=0.5、ε=10-4、nS=3，拓扑出相应的可打印构型，以 MBB 梁的S 方向和悬臂梁的W 方向为例，对优化构型进行几何重构，并对结构下边界与地面所成的夹角进行角度测量，证明所提出的单元密度更新迭代规则是可行的。

4.1 MBB 梁

将MBB 梁的设计域均匀离散为180×60 个单元，定义不同方向的基底，材料的弹性模量为1，泊松比为0.3，集中载荷F=1（所有量为相对值，无量纲，下文同），如图3 所示。以柔度最小化为目标，添加单元密度迭代规则，分别拓扑出以不同基底的可打印模型，如图4 所示。图中的粗实线表示增材制造的基底（下同）。

图3 MBB 梁基底方位Fig.3 Baseplate Orientation of MBB Beam

图4 添加迭代规则的MBB 梁拓扑构型Fig.4 MBB Beam Topological Configuration with Iterative Rules

4.2 悬臂梁

类似的将悬臂梁的设计域均匀离散为180×60 个单元，定义不同基底的打印方向，材料的弹性模量为1，泊松比为0.3，集中载荷F=1，如图5 所示。以柔度最小化为目标，添加单元密度迭代规则，分别拓扑出以不同基底的可打印模型，如图6 所示。

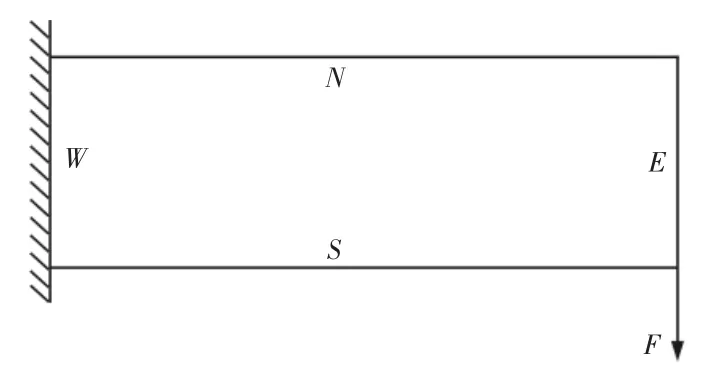
图5 悬臂梁基底方位Fig.5 Baseplate Orientation of Cantilever Beam

图6 添加迭代规则的悬臂梁拓扑构型Fig.6 Cantilever Beam Topological Configuration with Iterative Rules

4.3 约束的角度验证

虽然以不同方向为基底的拓扑出来的结构不同，但是均能满足倾角大于63°的要求，实现无附加支撑的打印，如图4、图6所示。为了更严谨的验证提出的单元密度更新迭代规则的是可行性，分别对MBB 梁的S 方向和悬臂梁的W 方向基底的拓扑构型进行模型重构，并对典型的倾角进行测量，其测量结构，如图7、图8 所示。从测量结果可知，无论是MBB 梁还是悬臂梁其倾角都大于或者等于63°，进一步说明所提出的单元密度迭代规则是有效的。