一种RBF 神经网络的直接自适应滑模轨迹跟踪控制设计

2020-11-23王文娟

机械设计与制造 2020年11期

王文娟，李俊

（江西应用科技学院人工智能学院，江西南昌 330100）

1 引言

轨迹跟踪问题一直是飞行器制导控制领域研究的热点和难点，结合不同的问题背景，应用不同的控制方法，可以形成不同形式的轨迹跟踪控制律[1]。针对运动模型的非线性和高度耦合特性，对此问题的处理思路大致可分为两类，一类是基于小扰动线性化[2]或邻域最优控制理论[3]对模型进行近似线性化，然后采用线性控制方法设计控制律。该类方法设计过程简便，工程上易于实现。但当干扰与模型不确定性造成的实际弹道与标称轨迹偏差较大时，其跟踪精度较差。

另一类思路是直接采用非线性方法进行控制律设计[4－5]，该类方法的设计过程复杂，控制律的实现需用信息多，工程应用较困难。针对上述问题，采用滑模变结构的策略设计控制律，该方法与其它非线性方法相比无须在线系统辨识，物理实现较简单，且其对参数摄动和干扰不灵敏，良好的鲁棒性利于工程应用[6]。但是滑模控制器内在不连续的开关特性会造成抖振现象，对抖振的削弱一直是滑模控制理论的研究热点，国内外学者针对此问题提出了不同的解决方法，如设计边界层[7]、滤波方法[8]、干扰观测器方法[9]等。这些方法从不同的角度提出了解决思路，每一种都有其相应的优点与局限性。将径向基函数（RBF）神经网络与滑模控制相结合，通过RBF 网络对非线性系统的自适应逼近来降低切换增益，削弱抖振。且其能以任意精度逼近任何非线性函数，具有唯一最佳逼近特性。另一方面，RBF 网络构简单，收敛速度很快，非常适合在线的实时控制[10]。

2 飞行器运动模型

以战术导弹中制导段的运动模型为研究对象，因其朝向预测命中点飞行，在实际飞行的过程中，由随机干扰产生的侧向运动参数的变化量都是小量，其飞行弹道与纵向平面内的弹道差别不大，因此可以将纵向运动和侧向运动分开来研究。主要考虑纵向平面轨迹跟踪系统的设计，其质点运动模型为：

式中：v—导弹速度；θ—弹道倾角；x—横程；h—纵程；α—攻角作为控制量；P，Cx，Cy，q，S 等参数的表达式均参考文献[2]。

在战术导弹设计阶段，一般先进行速度特性设计，从而确定发动机参数，所以导弹速度近似认为是不可控量。另一方面，设计中制导律的目的是引导导弹沿基准弹道飞向预测命中点，对导弹的速度大小没有必要进行精确跟踪。对于剩余三个状态变量，只要能对θ，h 稳定跟踪，即可实现对基准弹道的稳定跟踪，所以取θ，h 为系统状态变量。此外，由于战术导弹主动段发动机造成的误差较大，通常不对弹道进行精确跟踪，而是采用方案飞行，对于无动力段即中制导段，可以对运动模型进行如下简化，系统状态方程变换为：

根据式（5），对高度求二阶导，并令x1=h，可以将上述模型可以转换为如下的一个非线性二阶系统：

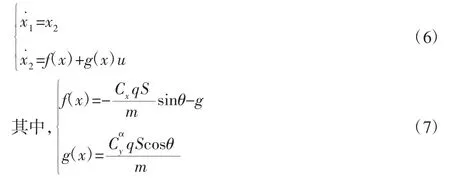
3 滑模跟踪控制律

考虑上节得到的二阶非线性系统式（6），只要实现对x1，x2的精确跟踪即可实现对弹道的精确跟踪。选择如下的滑模面：

式中：hr—标称弹道的飞行高度，c=［c 1］满足赫尔维兹条件。

对式（8）进行求导：

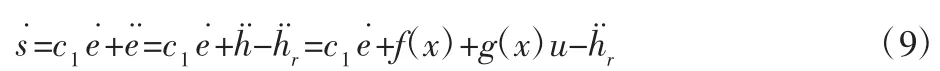
滑模控制器的设计通常由两种思路，一种思路是设计趋近律，通过趋近律与所选择的滑模面联立推导得到控制律；另一种思路如下：

定理1 对于式（6）所示的非线性系统和式（9）所选择的滑模面，满足（fx），g（x）为光滑函数设计如下的理想滑模控制器：

证明：导弹沿标称弹道飞行，其实际轨迹应在标称轨迹的邻域内，此时显然f（x），g（x）是光滑函数，g（x）有界；在无动力段，弹道倾角的变化范围属于且不接近 0，不会产生奇异现象。

取Lyapunov 函数为：

对式（11）求导，可得：

将式（9）代入式（11），可得：

将式（10）设计的滑模控制器代入式（13），可得：

综上，采用式（10）设计的滑模控制器，弹道跟踪系统是稳定的。

4 RBF 神经网络直接自适应控制

在实际飞行中，参数摄动及各种随机干扰造成f（x），g（x）难以精确获得，采用滑模控制理论设计跟踪控制律时，这种建模的不确定性会产生较大的切换增益，进而造成较大的抖振。针对此问题，本节采用自适应RBF 神经网络逼近第二节所设计的滑模控制器。

4.1 神经网络调参律

RBF 神经网络是一种局部逼近的神经网络，其基函数通常选取为如下的高斯基函数：

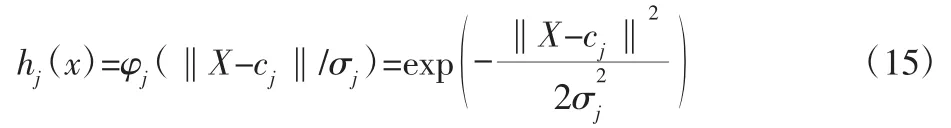
式中：下标 j—第 j 个基函数；cj—基函数中心点；σj—基宽参数；φj—径向对称函数。

RBF 神经网络的结构由输入层和输出层两层组成，输入层实现输入信号到隐含层节点的非线性映射，输出层实现隐含层节点到输出信号的线性映射。为了实现对滑模控制器u 的逼近，选择如下的网络输入：

将控制器作为神经网络的输出，其映射关系结构图，如图1 所示。图中隐含层节点向量为H=［h1，h2，…h9］T，相应的中心点向量和基宽参数向量分别为：C=［c1，c2，…c9］T，σ=［σ1，σ2，…σ9］T。

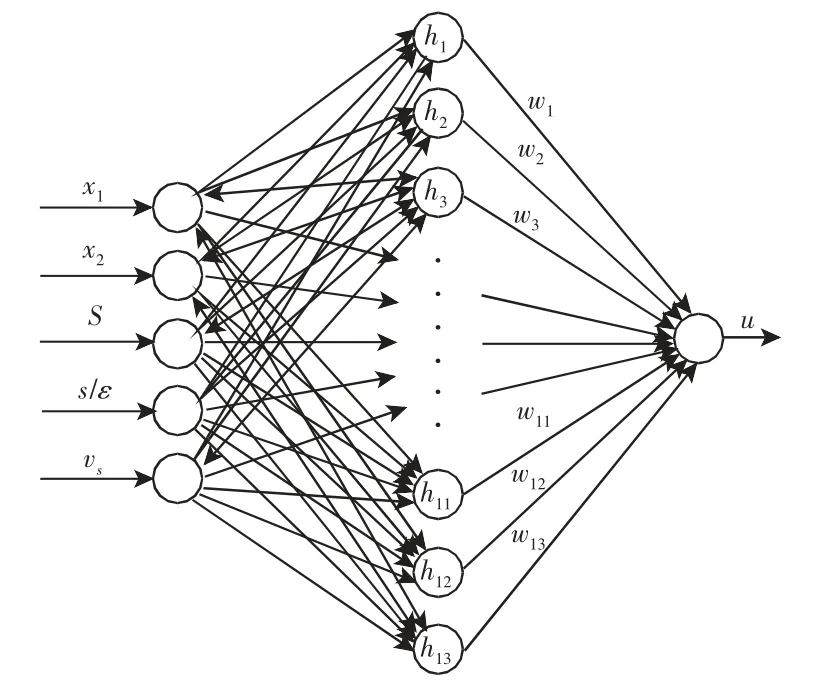
图1 神经网络结构设计Fig.1 Structure of Neural Networks

神经网络输出的表达式为：

RBF 网络具体的学习过程可以分为两个阶段。第一个阶段是无监督学习，其作用是根据输入的样本确定隐含层的高斯基函数的中心点向量cj与基宽参数σj。采用K-均值聚类算法实现中心向量的调整，具体步骤如下：

（1）首先初始化隐含层各个节点的中心向量值cj（0）（j=1，2，…，9），学习步长 β（0），（0＜β（0）＜1）及误差阈值 δ。

（2）根据输入样本X（k），计算欧氏距离，确定与样本距离最小的隐含节点。计算公式如下：

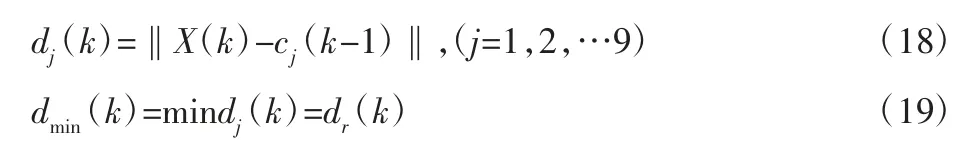
式中：k—输入样本的序号；r—与样本距离最小的隐含节点序号。

（3）进行中心调整。

由式（22）可知，随着输入样本的增多，学习步长逐渐减小，最后趋于0。

（4）对于所有的输入样本重复进行步骤（2）和（3），直至样本总误差小于所设定的误差阈值。

基宽参数由所选取的中心向量的最大距离确定，具体算法如下：

式中：D—中心向量之间的最大距离。

第二个阶段是有监督学习，该阶段训练隐含层到输出层之间的权值。由于隐含层到输出层为线性映射，所以训练连接权值W 是一个线性优化问题，其解是唯一的，不存在局部极小值。连接权值的学习算法设计为：

式中：η—学习效率，为了保证学习算法的收敛性，通常取0＜η＜1；ud，u（l）—网络的期望输出与实际输出。

当样本离中心向量较远时，hj非常小，可以当作0 处理。只有当hj大于某一数值（如0.05）时才会对权值进行相应修改。因此隐含层节点向量H 中只有个别元素为1，其余为0，每次训练时只有少数几个权值需要调整，从而保证了RBF 较快的学习速度。

4.2 控制器的设计与分析

对于图1 所示的神经网络结构，其理想的输出为：

式中：μl—逼近误差，且 μl有界，即|μl|≤μ0。W*—理想的连接权值：

连接权值的鲁棒更新算法设计如下：

式中：Γ=ΓT＞0—自适应增益矩阵；σ—大于零的常值，当存在神经网络逼近误差及外界干扰时，σ—修正能够提升自适应控制器的鲁棒性。

将式（28）代入式（9），可得：

将式（26）代入式（30），可得：

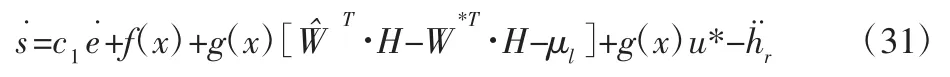
将式（10）代入式（31），可得：

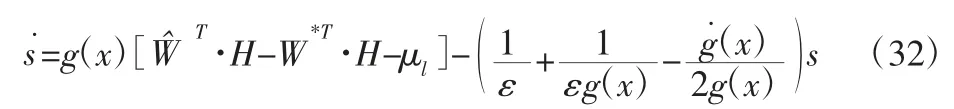
在设计Lyapunov 函数时考虑包含滑模面与鲁棒自适应律，为了使自适应律中不出现g（x）项，将Lyapunov 函数中的项用代替，具体表达式如下：

对式（32）求导，可得：

在式（34）中：

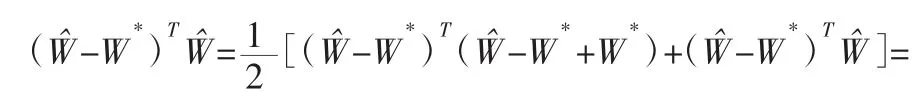
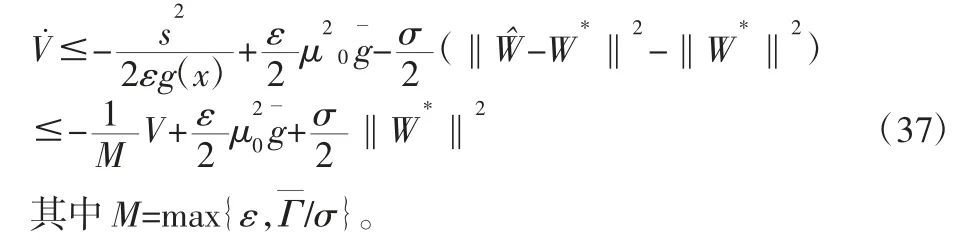
引理 1 对于半正定函数 V 的不等式方程组V˙≤-αV+f，α 为任意常数，在任意的t≥t0≥0 上的解为：

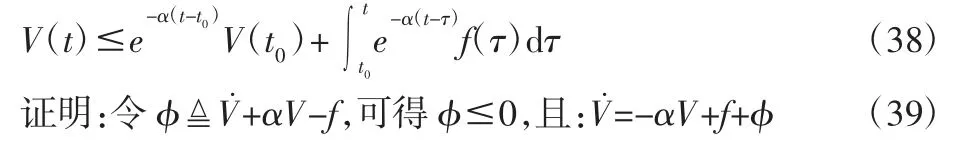
微分方程的解为：

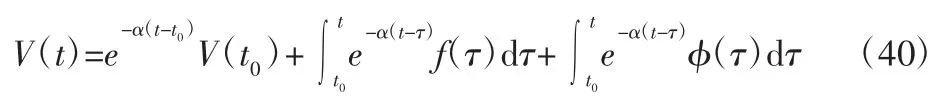
又因为对任意的 t≥t0≥0，有 φ（τ）≤0，即：

综上，引理得证。

对于式（37），令 t0=0，根据引理 1 可得：

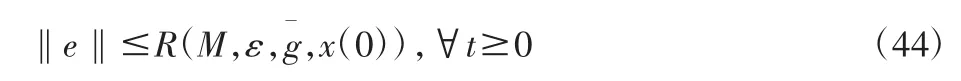
定义如下的初始紧集：

因为初始状态必须包含在紧集Ω0里，所以控制器是局部稳定的。这样定义是合理的，因为只有在一个紧集内，神经网络近似才是有效的[10]。

对于所有的x（0）∈Ω0，设计参数值的大小由如下表达式决定：

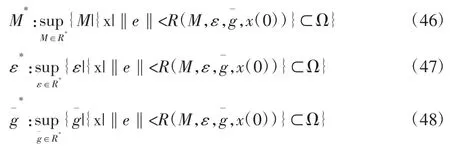
为了保证x∈Ω，∀t≥0，选取控制器参数时应满足M≤M*，ε≤ε*

5 仿真验证

为了所设计控制律的有效性，仿真工况条件设置如下：分别给定三组初始误差，加入等效攻角为（-1～1）deg 的随机风干扰，并对气动参数施加30%的摄动，采用所设计的控制律验证能否有效消除跟踪误差，实现轨迹精确跟踪。模型中各参数的取值参考文献[2]，三种情景的具体参数，如表1 所示。

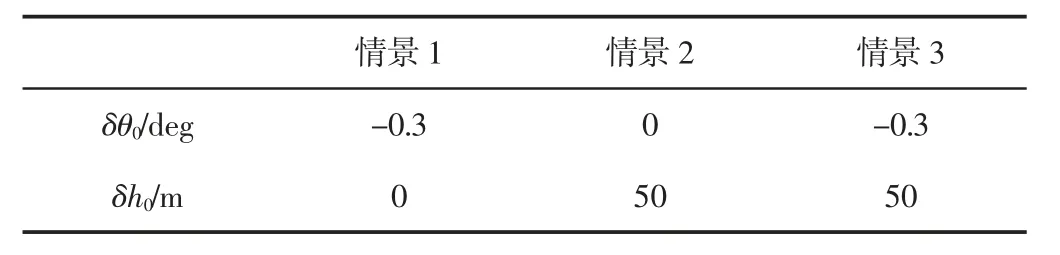
表1 仿真条件Tab.1 Simulation Conditions

图2 情景1 跟踪误差Fig.2 Tracking Errors of Case 1

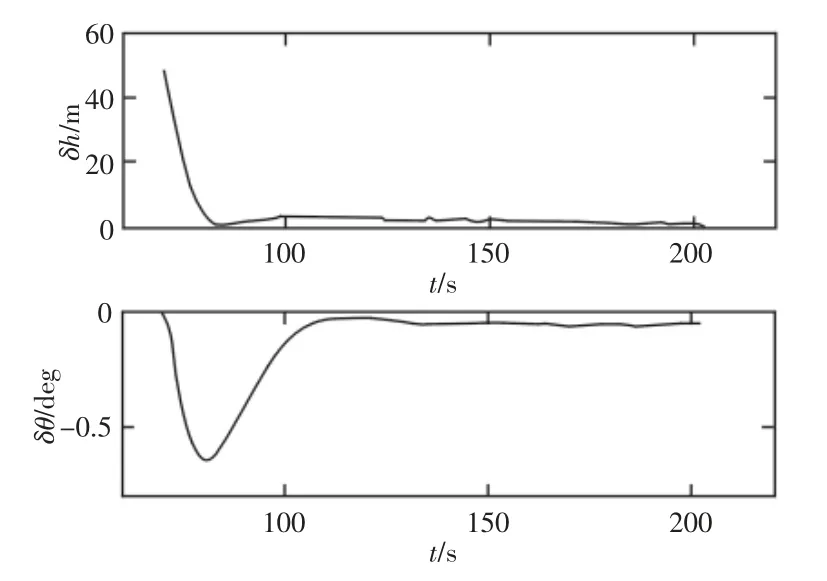
图3 情景2 的跟踪误差Fig.3 Tracking Errors of Case 2

图4 情景3 跟踪误差Fig.4 Tracking Errors of Case 3

由图2～图4 可知，当存在随机干扰和参数摄动的情况下，无论是给弹道倾角和高度状态量的其中之一施加初始误差，还是给两者同时施加初始误差，其都能有效消除跟踪误差，实现轨迹的精确跟踪。同时在三种情景下，误差曲线都较为光滑，说明了引入RBF 神经网络可以有效削弱由滑模控制不连续的开关特性造成的抖振现象。为了验证所设计的控制律对不同初始误差的适应性，分别将高度误差设置为［-50，50］m 内的随机值，将弹道倾角误差设置为［-0.3，0.3］deg 内的随机值，进行20 次蒙特卡洛仿真，仿真结果，如图5 所示。由图可知，该控制律在不同初始误差组合下，都能够有效消除误差，实现对轨迹的精确跟踪。