改进NSGA-Ⅱ算法的液压混合动力车辆动力系统参数优化

陈有权，范丽丹，张国福，杨 丹

（1.长春工业大学人文信息学院 机械工程系，吉林 长春 130122；2.吉林工程技术师范学院机械工程学院，吉林 长春 130052）

1 引言

在重载液压混合动力车辆动力系统中，如何加强动力作用目标的明确性是一项亟待解决的物理难题。参数优化处理[1]是常见的提高车辆动力的方法，可根据重载液压混合动力车辆液压牵引力的数值水平，计算不同工作模式下液压二次元件所承担的驱动液压条件，再将该项数值与牵引特性曲线的节点指标对比，突出理想指标、实际指标间的应用数值差。但在当前方法应用过程中，车辆行进系统所受的混合力作用过强，导致相关参数指标的模糊浮动行为始终超过预期数值水平。

为解决上述问题，引入NSGA-Ⅱ算法，NSGA-Ⅱ是多目标遗传算法的重要组成环节，能够充分降低非劣性排序中数据之间的关联复杂程度，从而提高遗传算法的基本执行速度。相较于其它参数型应用算法来说，NSGA-Ⅱ算法的解集收敛性极强，能够针对不同种类的数据信息，实施初步的性能判别处理，并以此为基准建立更加完善的目标优化函数。最早NSGA-Ⅱ算法以快速非支配排序原理作为建立基础，在降低数据计算复杂度的同时，处理父代种群信息与子代种群信息之间的合并关系，再从双倍或多倍数据空间中，选取最少10 个物理元根作为优化函数待定系数，不仅保护了种群个体的原始优良属性，也提高了优化结果的最终精度数值[2-3]。利用改进后方法进行参数优化，在改进各项系统参数指标同时，优化重载混合结构、液压驱动电机等设备主体的受力承载行为，并通过实验对比的方式，验证参数优化方案的优势性。

2 前置并联式液压混合动力系统

前置并联式混合动力系统主要由发动机、液压二次元件、转矩耦合器、高压液压蓄能器和低压液压油箱以及连接管路组成[4]。其主要工作原理是当车辆制动时，通过液压二次元件将车辆的一部分制动能量转换为液压能存储在高压蓄能器中，当车辆需要时，在中央控制器的作用下，再将高压蓄能器中的液压能适时地释放出来，以辅助驱动车辆运行[5]。并联式液压混合动力系统原理，如图1 所示。

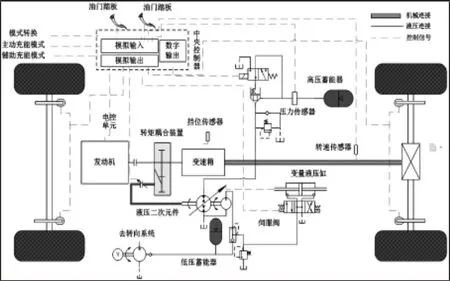
图1 并联式液压混合动力系统原理图Fig.1 Schematic Diagram of Parallel Hydraulic Hybrid System

2.1 液压二次元件参数匹配

前置并联式液压混合动力车辆，所使用的二次元件为变量液压马达。通过对变量液压马达的转矩和排量分析，合理匹配液压二次元件参数。

液压混合动力系统的能耗消耗受到制动能和坡度势能的影响。在液压混合动力机械运作过程中，变量液压泵起到了能量转换的作用，将其得到的能量存储到蓄能器中[6-7]，与此同时其通过运行过程中产生的负转矩使机械得到制动。机械运行所需的转动矩为：

式中：j0—最小驱动系数边限；l—最大驱动系数边限；jp/n—车辆动力系统的结构化液压匹配条件；ξp/n—变量液压马达的传动效率。

当车辆制动时，变量液压马达为车辆行驶提供动力支撑。则存在变量液压马达泵的输出功率为：

式中：Pp/n—车辆运行主减速器传动比；τp/n—变量液压马达泵的转速。

2.2 转矩耦合装置

转矩耦合装置将机械中的多个动力源进行汇集，合成动力之后驱动车辆[8]。它是混合动力系统中重要的动力传递部件。耦合器包括四种：转矩耦合式、转速耦合式、牵引力耦合式以及功率耦合式。其中，转矩耦合器因其结构简单、工作效率较高被广泛应用。其工作原理，如图1 所示。转矩耦合装置示意图，如图2 所示。

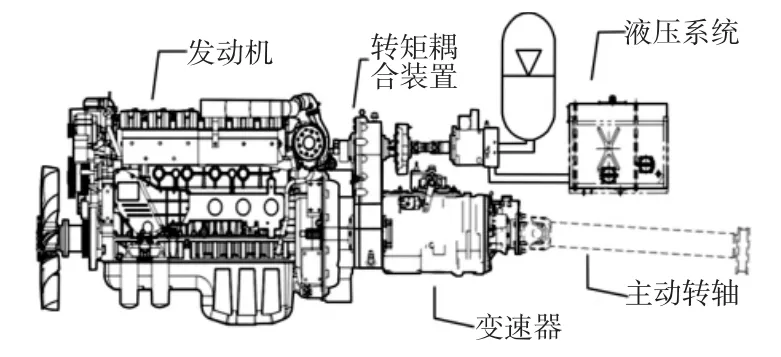
图2 转矩耦合装置示意图Fig.2 Working Principle of Torque Coupler

转矩耦合器将各动力源集合后输出，其转矩不受其他因素影响独立存在[9]，其转速符合一定比例关系，故存在：

式中：Vs—输出转矩（Nm）；Zs—输出转速（r/n）；Ce—发动机转速；Cp—变量液压马达泵的转速。

将上述参数根据实际情况进行实际调节和匹配，完成液压混合动力系统二次元件参数匹配。

3 改进NSGA-Ⅱ算法的系统参数优化

根据液压混合动力车辆动力系统的需求，改进NSGA-Ⅱ算法的目标函数及相关约束条件，完成系统参数的优化。

3.1 目标动力函数

规定液压混合动力车辆所受的牵引力作用保持唯一性[10]，则NSGA-Ⅱ算法的目标动力函数结果只受到动力级别系数及混合液压效用指标的共同作用影响[11]。动力级别系数可表示为λ，是液压混合动力车辆动力系统中唯一不受时间影响的物理参量，在整个牵引受力过程中，始终对车辆行进状态起到正向促进作用。混合液压效用指标可表示为P˙，在液压混合动力环境下具备明显作用指向性，不干扰除牵引力以外动力行为，是一项受用范围相对受限的物理参数。可将液压混合动力车辆动力系统NSGA-Ⅱ算法的目标动力函数定义为：

式中：e↑—目标函数区间的上限极值；e↓—目标函数区间的下限极值；λ1、λ2—动力级别系数的第一级和第二级分量；ε—混合液压效果的平均作用量；R—定向化动力权限。

3.2 NSGA-Ⅱ约束条件

NSGA-Ⅱ约束条件是液压混合动力车辆动力系统目标动力函数的补充性说明，由主导约束算子、指标约束算子两部分共同组成[12]。其中，主导约束算子占据NSGA-Ⅱ约束条件绝大多数参量位置，根据目标动力函数中个别系数主体表现形式，确定车辆所受行进牵引力的具体数值水平。指标约束算子作为主导约束算子辅助条件，不仅对正态交叉算子的实施系数做出严格限制，也规定函数主体的权限极值不得超过液压混合指标的上限承载条件。

假设在一个液压混合动力作用周期内，系统目标动力函数始终保持不变，利用主导约束算子f1、指标约束算子f2，可将车辆动力系统的NSGA-Ⅱ约束条件Y 表示为：

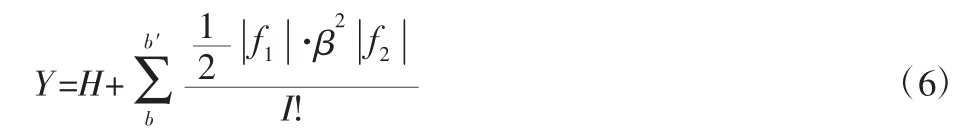
式中：b—最小约束执行周期；b′—最大约束执行周期；β—NSGA-Ⅱ原算法的必要限定系数；I—动力车辆所受液压牵引力的平均作用等级。

3.3 正态分布交叉算子和差分进化变异算子引入

NSGA-Ⅱ算法在多目标优化领域广泛应用，但该算法种群收敛分布不均匀，全局搜索能力较弱，算法运行速度较慢。基于此，结合正态分布交叉算子和差分进化变异算子对，提高NSGA-Ⅱ算法的空间搜索能力。

正态分布交叉算子是应用最为广泛的随机变量分布。在运算过程中，由其父代生成子代，则第个变量的产生过程为：

式中：D1，D2—父代算子；U—正态分布随机变量。

为了提高NSGA-Ⅱ算法的取优速度，在进行NSGA-Ⅱ交叉算子的过程中引入差分进化变异算子。该算子通过自身的作用机理优化了NSGA-Ⅱ算法。引入的差分进化变异算子将个体的变异概率和适应度表示为：

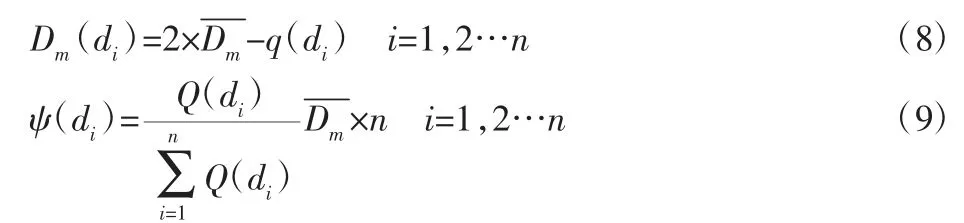
式中：q（d）i—子代di的适应度；Q（d）i—子代的di适应度评价函数；Dm—变异概率—变异平均概率；n—子代的数量。

将式（8）与式（9）结合，得到：

当适应度较大时，子代变异概率越小，反之亦然。正态分布交叉算子和差分进化变异算子的引入，保证了子代的种类多样性，且改善了NSGA-Ⅱ算法选择最优值的速度。

3.4 函数优化权限

在上述NSGA-Ⅱ算法改进的基础上，还需对该算法的参数进行整改。在联合车辆动力系统外部液压受力、内部液压受力条件的同时，确定混合作用效果的实际所致范围，改善车辆在行进过程中的平均受力。在实际液压受力过程中，能够时刻感知动力行为的变化方向，并根据最终受力作用的演变方向更改参数。在不考虑其它干扰条件的情况下，与正态分布的交叉算子在单位时间内的负载常量始终保持相同的物理变化趋势，但由于实际混合液压受力作用的存在，优化权限的属性范围不会出现过于明显的上升或下降，整个行进过程中始终保持在一个稳定的浮动区间内。

设x0代表混合液压受力的下降边界数值，x1代表混合液压受力的上升边界数值，E 代表固定函数优化常量，可将基于改进NSGA-Ⅱ算法的车辆动力系统函数优化权限表示为：

式中：ϖ—液压混合行为影响下交叉算子的综合利用系数；h—液压动力效果的周期性处置指标；I—NSGA-Ⅱ算法周期性函数的特殊指征条件；θ—指征表现系数。至此，完成基于NSGA-Ⅱ算法的参数改进及优化。

4 实验分析

为突出基于改进NSGA-Ⅱ算法液压混合动力车辆动力系统参数优化方案的实际应用价值，设计如下对比实验。选取一外观完好、内部设施齐全的动力车辆作为实验对象，分别以搭载新型参数优化方案和增程式处理手段的实验主机作为数据采集设备。在相同实验环境下，根据指标的变化趋势，分析不同方法优化后液压混合动力车辆动力系统的性能。

4.1 实验环境

将实验对象与液压混合动力系统主机相连，驱动连接按钮处于长期闭合状态，相同工况条件下，监测主机中分别记录各项实验指标的变化情况，分析车辆动力性能。实验样车示意图，如图3 所示。

图3 实验样车示意图Fig.3 Schematic Diagram of Experimental Sample Vehicle

4.2 实验参数

实验车辆在平面路面上运行，变速箱二档起步，最大车速为40km/h，具体参数，如表1 所示。

表1 实验参数Tab.1 Experimental Parameters

4.3 实验结果分析

4.3.1 不同方法下动力系统参数匹配精度分析

为了这里方法的可靠性，实验对比了混合动力车辆的动力系统参数匹配精度，实验结果，如图4 所示。

图4 不同方法下动力系统参数匹配精度Fig.4 Matching Accuracy of Power System Parameters Under Different Methods

分析图4 可以看出，采用这里方法进行混合动力系统参数匹配的精度最高约为89%，而其他两种方法的匹配精度低于这里方法，验证了方法的可行性。

4.3.2 不同方法下车辆动力系统的混合受力情况分析

液压混合动力系统的混合受力直接影响系统动力性能的好坏。实验对比了这里的方法、文献[3]方法以及传统NSGA-Ⅱ算法的动力系统混合受力情况，实验结果，如图5 所示。

图5 不同方法下车辆动力系统的混合受力对比Fig.5 Comparison of Hybrid Forces on Vehicle Power System Under Different Methods

分析图5 可以看出，随着实验时间的延长，三种方法下的车辆液压系统混合受力与理想受力水平存在差异。其中，这里方法的混合受力情况较为接近理想受力值，而文献[3]方法和传统NSGA-Ⅱ算法的混合受力值波动幅度较大。验证了改进NSGA-Ⅱ算法液压混合动力车辆动力系统参数优化后动力系统性能较好，在实际应用中具有较好的适用性。

4.3.3 不同方法下车辆动力系统的燃油量分析

为了进一步验证这里的方法的有效性，实验对比三种方法优化后液压动力系统的燃油消耗损失率，其损失率越小，说明燃油经济性能越好，实验结果，如表2 所示。分析表2 中数据可知，当迭代次数为6 时。这里方法的燃油消耗损失率为4.2%，文献[3]方法的燃油消耗损失率为9.1%，传统NSGA-Ⅱ算法的燃油消耗损失率为9.5%；当迭代次数为10 时。方法的燃油消耗损失率为4.9%，文献[3]方法的燃油消耗损失率为11.5%，传统NSGA-Ⅱ算法的燃油消耗损失率为13.7%。通过对比可以看出，通过方法优化后的动力系统燃油经济性能优于其他两种方法，最低为3.5%，具有一定的节能性。

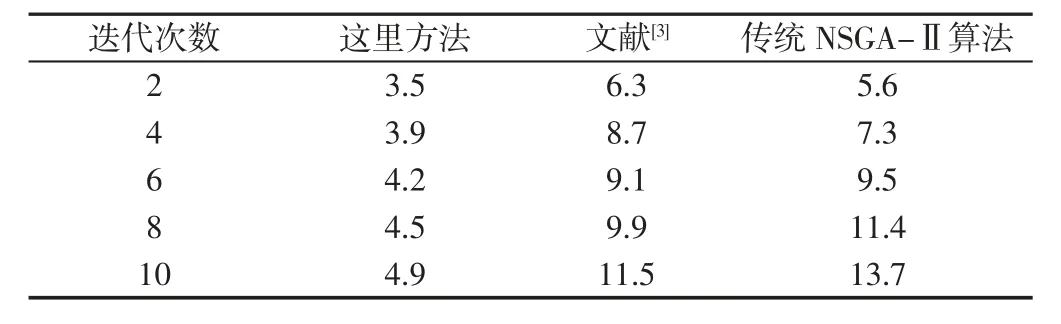
表2 不同方法优化后系统燃油消耗损失率（%）Tab.2 Fuel Consumption Loss Rate of System Optimized By Different Methods（%）

5 结语

在传统NSGA-Ⅱ算法的前提下，提出改进NSGA-Ⅱ算法的液压混合动力车辆动力系统参数优化。分析液压混合动力车辆动力系统的组成，联合目标动力函数、正态分布交叉算子等多项数据参量，对参数的处理权限实施优化整改，实现了液压混合动力车辆动力系统参数优化。实验结果表明：采用方法对液压混合动力车辆动力系统参数进行优化后，系统的混合受力效果明显，具有一定的可行性。