感应电动机调速系统运行速度跟随控制方法
2020-11-23王丽静张建军王丽君
王丽静,张建军,王丽君
(1.西安石油大学,陕西 西安 710065;2.陕西国际商贸学院,陕西 咸阳 712046)
1 引言
感应电动机工作中保证定子磁链幅值不变,并确定出交流感应电机定子的工作频率与电压变化的幅值区间,即可以在不改变感应电动机转矩输出和工作频率的前提下,实现对电机当前速度的识别与跟踪控制[1]。在恒压频比控制的基础上,增加了交流感应电动机的调速范围,适用于市面上大多数感应电机变频器控制。
现阶段感应电动机调速系统速度识别与控制的方法,以非线性静态控制为主,例如文献[2]分析对每个方向的研究状况,针对滑模变结构控制原理,将其分为18 个研究方向,并对滑模控制的未来发展作出展望。文献[3]考虑到变换器中寄生电阻存在,针对期其负载稳定性降低以及不能稳定运行的问题,基于无源性的控制方法,观测变换器中寄生电阻状态,并应用非线性函数对其进行改进。文献[4]基于模糊PID 控制算法,建立3-RRR 平面并联机构控制系统,并搭建机构控制实验装置,研究机构角位移误差的影响要素,形成3-RRR 平面并联机构实时控制方法。
但是以上方法存在动态性能不强、控制与识别精度低、算法复杂不易实现等缺点。为达到精准控制的目的,从建立动态数学模型的视角出发,提出一种对感应电动机的磁场定向实时控制方案。其创新之处在于在高性能的调速系统中,感应电机出现的自恃震荡现象会影响到系统的性能,转子工作中存在时间常数的估计偏差,增加了调速系统的周期性震荡,因此基于动态数学模型解耦定子与转子之间的电磁关联,提高方法对感应电动机速度的辨识精度与速度跟随控制性能。
2 感应电动机调速系统速度矢量控制数学模型
为实现对感应电动机调速系统运转的高性能跟随控制,基于数学模型对调速系统的运动过程做高阶非线性分析。感应电动机产品容量为阶梯性分布,无论是转数差控制还是恒压比频控制,都会造成一定能耗的浪费,跟随控制方法根据调速系统的运行情况控制磁通的变化,能够达到提高电机效率,减少能源无谓消耗的目的。基于电动机转子的空间坐标关系建立矢量控制模型,感应电动机转矩会受到磁通、转子的通过电流和功率角度等因素的影响,各影响因素之间具有高度耦合性,导致系统的调速功能衰减,设感应电动机的电磁转矩为we:

式中:λ—感应电动机电磁转矩的系数;i—通过感应电动机的电流;ω—感应电机功率角速度;η—电机调速系统的磁通。采用数学矢量模型可以模拟更为直观、简单的直流电机控制模式,达到改善调速系统性能的最终目的[5-6]。感应电动机调速系统电磁转矩变化过程中,常用的三种定子坐标系速度矢量重叠,如图1 所示。
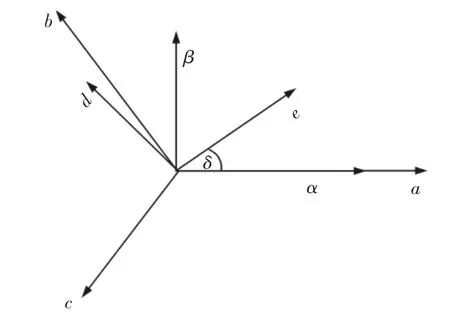
图1 三类定子坐标系旋转投影关系示意图Fig.1 Schematic Diagram of Three Types of Rotational Projection in Stator Coordinate System
在由三种坐标系复合组合的调速控制系统中,abc—坐标系的三个分量成120°夹角,该坐标系统任意一个分量在直角坐标系统α、β—坐标系上投影可得到唯一的投影分量;de—坐标系是α、β坐标系逆时针旋转δ 角度得到。给感应电动机abc 坐标系的三个轴向输入正弦交流电使其产生电磁感应,ω—电机的旋转速度;给相互垂直的两项绕组输入交流电合成电磁电动势,同理也给de 坐标系输入交流电形成绕组磁链,做相应的坐标转换产生等效的磁动力[7]。由abc 坐标系转换到α、β 坐标系用数据矩阵Habc表示为:

由α、β 坐标系转换到de 坐标系用数据矩Hαβ阵表示为:

对三个相关的坐标矩阵进行逆变换得到两项旋转电磁绕组的电压、电流、磁链等信息,即可以基于磁链坐标系调速系统控制模型,辨别出当前时刻感应电动机的运行速度,并对运行速度实施有效跟随控制,适应更多的应用条件。
3 基于模型的调速系统运行速度辨识
感应电动机调速系统转数识别是矢量控制核心环节,基于速度矢量控制自适应模型系统观测电机系统转子的运行速度,系统模型主要由于数据参考模型,可调模型与自适应模型构成,系统的整体工作流程,如图2 所示。
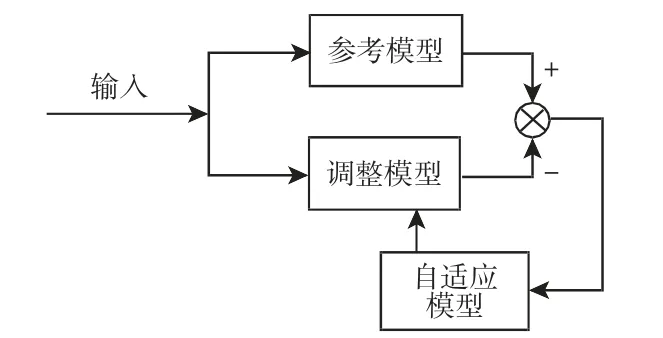
图2 电动机调速系统各模型整体工作流程Fig.2 Overall Work Flow of Each Model of Motor Speed Control System
将传感器采集到的数据输入速度矢量控制模型中的参考模型和调整模型,得到一对输出值y 和y′,改组性能指标值存在差异,经过模型的比较与处理后得出结果并输入自适应模型机构调整,将差值的结果逼近至零。定义三相abc 坐标系三个方向的矢量电流分别为 ia、ib和 ic,两相静止坐标系下矢量电流为 iα和 iβ,逆时针旋转δ 角度得到坐标系的矢量电流为ic和id,基于上节中的速度矢量控制模型能够计算得出各个方向的磁链幅值φr和转角速度ωr。基于磁链的运行速度观测要得到电动机真实转速信号与电流信号,才能保证对速度矢量测量的准确性[8]。依据感应电动机调速系统相对静止状态下磁链方程与转矩方程,得到电流参考模型矩阵方程:

式中:T—观测时间周期;κ—模型电路中的定子漏电感,以电流观测模型的结果作为参考值,通过测量电机系统中转子的电压值与电流值,能够提取到更为完整电流信号和可调节参数[9]。
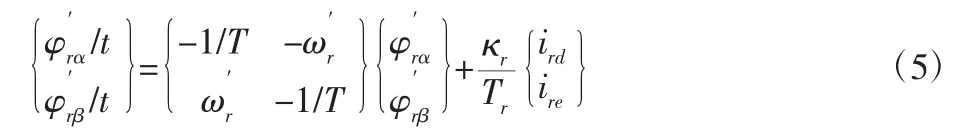

当速度矢量控制模型处于稳态变化时对应的转子磁链区域平衡,偏差信息的值达到最小,在该时刻能够辨别出感应电动机调速系统的当前运行速度,及速度区间是否处于正常的控制区间。
4 基于改进价值函数的速度跟随控制
为增强调速系统速度跟随控制方案的鲁棒性和抗干扰能力,基于价值函数设计速度跟随策略对电磁转矩实施控制。由于感应电机系统运动中,电气时间常数要远小于机械时间常数,当采样周期逐渐变小,可以以周期参考值T 作为电磁转矩的参考指标。以电磁转矩、系统电流、最佳转数分别为状态变量设计一组电磁参考值价值函数G1:
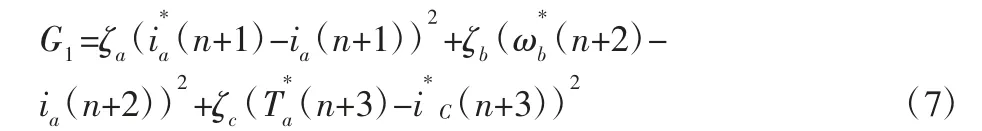
式中:ζa—电动机系统电流的平方误差;ζb—感应电动机当前速度误差;ζc—电磁转矩的控制周期误差项。
对于经典价值函数进行优化,基于鲁棒性原则分别控制矩阵和参数电流的精度,并进行扰动补偿;以直流电流、电机旋转角度和电磁转矩作为模型优化的参考值,增强系统的学习能力和参数匹配能力;最后还对系统电流做优化处理,约束感应电动机调速系统的跟随控制效果。参数ζa、ζb和ζc的选定,对于跟随控制的效果具有重要的影响,具体的影响程度会随着参数权重比例关系的变化而变化。权重系统调整中,三个参数的量纲标准不同采用归一化处理方法两两确定参数的初始值,其中ζa=1/i,ζc=1/T ,in和Tn为感应电动机调速系统额定电机和额定功率;如果电机系统的电流脉冲不存在异常的波动,则无需调整ζb项所对应的电动机角速度,如果需要进一步改善的系统的性能,应保证ζa和ζc两个参数结果调整完成后,再调整从动参数ζb;最后从整体上权衡感应电动机调速系统输入电流的性能稳定情况和角速度的变化情况,对是哪个参数变量的权重比例关系做进一步微调整。
由动态跟随控制原理和矢量控制数学模型可知,电动机磁链、电感和电阻等参数匹配不适合会对系统电流的约束造成不利影响,进而导致控制策略失效,为此将参考电压作为新的变量输入跟随控制模型,设计关于感应电动机电压的价值函数G2:

具体执行步骤如下:
(1)测量电机的母线电压值ia和电机转子的当前角度和位置。
(2)分别观测 abc 坐标系三个轴向的电流值 ia、iC、ib,转矩参数,及电压的补偿量。
(3)利用矢量控制模型和式(7)、式(8)提取各轴向的电流值、电磁转矩和角度误差分析得出跟随控制速度的延时补偿。
(4)基于改进的电压价值函数,对感应电动机电流和电压进行限制,使感应电动机调速系统的运行速度始终处理设计数学模型的跟随控制范围,可以降低定子与转子系统发生故障的概率,改善感应电动机调试系统的性能。
5 数值仿真
5.1 仿真环境搭建与参数设置
在MATLAB 仿真环境下,验证文中提出基于速度矢量控制数学模型跟踪算法在转子运行速度辨识,及跟随控制等方面的应用效果。仿真实验的相关参数设置,如表1 所示。感应电动机调速系统需要根据不同情况改变系统的工作频率和工作电压,因此在实验中设计了一个可变的主控电路,执行系统的指令并影响到控制方法的性能,电路结构设计,如图3 所示。

表1 仿真参数设置Tab.1 Simulation Parameter Settings
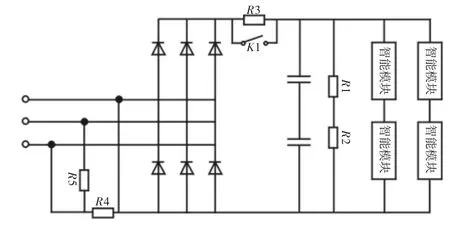
图3 可变主控电路设计Fig.3 Design of Variable Main Control Circuit
主控电路是调速控制系统的执行机构,根据主控电路的接入方式选择直流-交流变频,和交流-交流变频等两种不同的工作方式。
5.2 仿真结果分析
利用光电编码装置将感应电动机的真实运行速度信号传递到STM32 单片机中,并利用MATLAB 软件绘制出运行速度的变化曲线,如图4 所示。
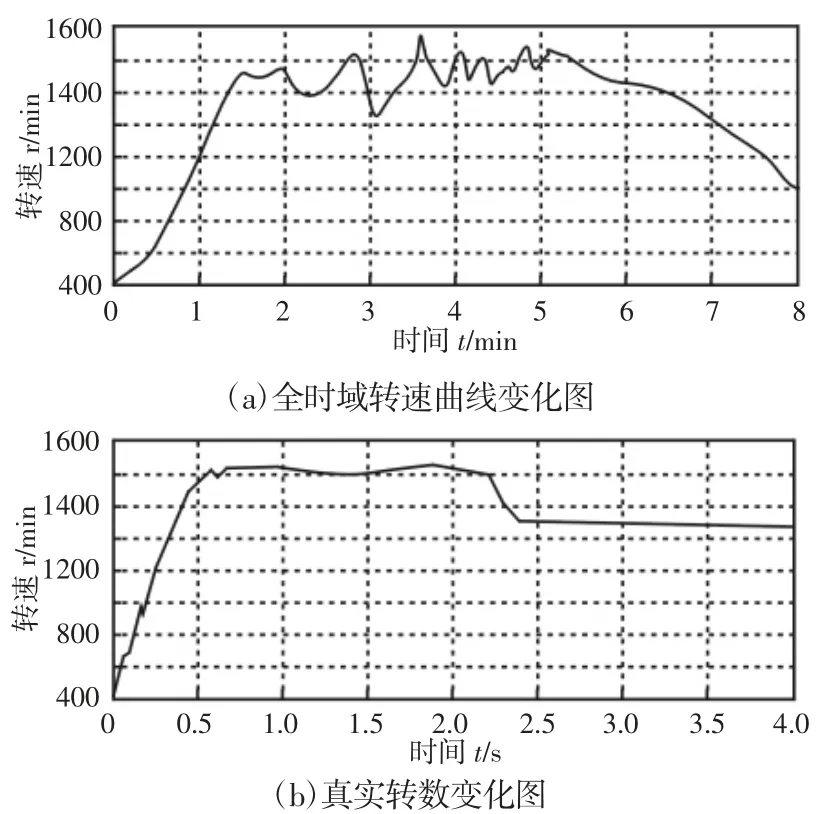
图4 仿真时间内调速系统的真实转数变化对比Fig.4 Real Revolution Change of Speed Control System in Simulation Time
首先给出MATLAB 仿真环境下文中提出方法对于转速的识别情况,如表2 所示。
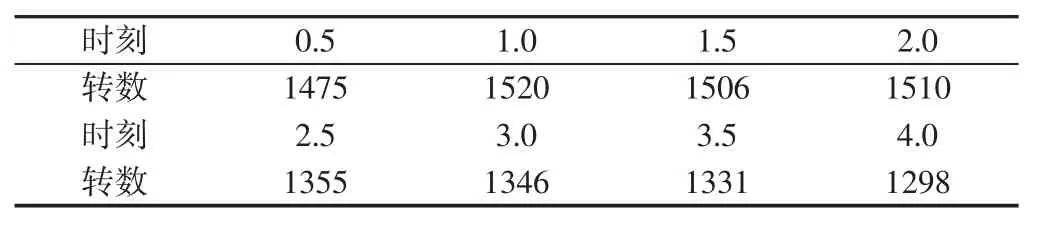
表2 文中速度矢量跟踪模型的转数识别情况Tab.2 Speed Vector Tracking Model Revolution Recognition
分析表2 数据与与图4 的曲线对比轨迹可知,提出方法对于感应电动机调速系统速度的识别趋近区域理论值,识别效果良好。再分别基于文献[2-4]三种传统控制方法,讨论其对运行转数的辨识情况的统计结构,如表3 所示。

表3 传统方法调速系统的转数识别情况Tab.3 Speed Identification of Traditional Speed Control System
从三种传统方法的电机运行速度识别结果能够分析出,辨识效果距离真实转数变化曲线的差距较大,方法的性能有待加强。且在于全时域转速曲线变化进行对比时,其曲线变化变化平缓,说明这里方法可以有效的调整系统转速。
其次利用MATLAB 仿真软件在4.0s 控制时间内仿真一个方波型运行轨迹,分别利用不同的方法进行速度的跟踪控制,结果,如图5 所示。图中:a、b、c、d—基于速度矢量模型的控制方法,文献[2]控制方法、文献[3]控制方法和文献[4]控制方法:
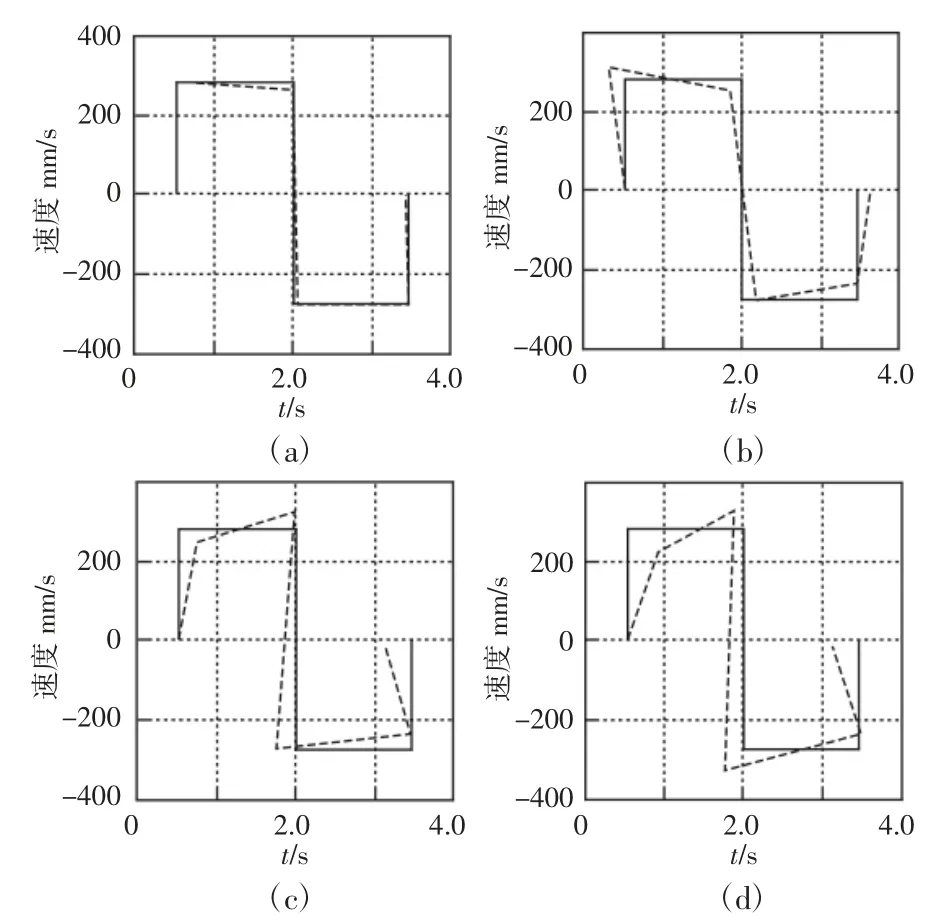
图5 跟随控制数值仿真结果对比Fig.5 Comparison of Follow-Up Control Results
跟踪控制结果显示,这里提出方法的控制效果与理论曲线重合度较好,而其他三种传统方法都出现不同程度的偏差。
6 结论
针对感应电动机调速系统速度跟随控制过程中的各种不确定情况,提出基于速度矢量数学模型的控制方案,改善系统的动态性能。从数值仿真的结果可知文中提出跟随控制方法的效果趋近于理论真实值,速度辨识效果和跟踪控制效果显著较优,能够大幅度提高感应电动机系统的性能。
