磁轴承飞轮储能系统非线性动力学研究

刘朝涛，王卓雅

（重庆交通大学机电与车辆工程学院，重庆 400074）

1 引言

随着新材料、新技术的迅猛发展，超导磁储能、飞轮储能、超级电容器、压缩空气储能等各种储能技术应运而生，并受到国内外专家学者的广泛关注[1-2]，其中飞轮储能以其功率密度高、循环寿命长、清洁环保无污染等[3-4]优良特性广泛应用于重载机车、电网系统、轨道车辆、电动汽车、卫星调姿等众多领域[5-7]。

飞轮转子在启停、外界激励作用下会产生不平衡力，使整机系统发生受迫振动，严重影响飞轮储能装置高速平稳运行[8]。文献[9]建立了基于轴向摩擦力矩与间隙变化刚度的双质量飞轮系统非线性动力学模型，分析飞轮设计参数对系统非线性特性的影响；文献[10]采用改进型拉格朗日动力学方法建立了卫星飞轮系统的非线性机电耦合动力学模型，并基于力学模型对系统动力学进行分析；文献[11]建立了飞轮储能系统径向非线性动力学方程，分析转子偏心条件下飞轮转速、磁轴承刚度对系统稳定性的影响。然而，基于电动机启停瞬间输入端激励扰动下，磁轴承飞轮储能系统径向与轴向的非线性动力学特性还鲜有研究。

基于Lagrange-Maxwell 动力学理论，建立磁轴承飞轮储能系统的非线性动力学微分方程，考虑电动机输入端激励对系统稳定性的影响，对磁轴承飞轮储能系统的非线性动力学模型进行分析，探讨输入端激励扰动与储能系统运动状态的映射关系；采用Runge-Kutta 法对飞轮储能系统非线性动力学进行数值仿真，通过时间响应历程曲线、相轨迹图、庞加莱图和幅值谱图综合分析激励振幅与频率对系统稳定性的影响规律，仿真结果为磁轴承飞轮储能系统设计中的参数优化匹配提供理论设计基础。

2 转子-磁轴承轴向运动受力分析

研究的飞轮储能系统主要包括飞轮、电动机、转子、轴向磁轴承和径向磁轴承，轴向、径向磁轴承分别用于平衡系统轴向和径向的不平衡力，维持系统处于稳定状态。储能系统转子由推力盘和转轴构成，推力盘一侧为轴向磁轴承，轴向磁轴承采用有偏置电流的差动控制方式，推力盘与磁轴承通过电磁力调节两者之间的相对位置，保证整个飞轮储能系统轴向偏移量在安全范围内，避免偏移量过大对整机系统稳定性造成不利影响。

当系统处于平衡位置时，推力盘和磁轴承间的气隙磁感应强度为：

式中：B1—左侧磁轴承气隙磁感应强度；B2—右侧磁轴承气隙磁感应强度；μ0—真空磁导率；N—线圈匝数；I—线圈偏置电流；δ0—平衡位置时磁轴承与推力盘间的气隙长度。

左右磁轴承产生的电磁力为：

式中：As—轴向磁轴承的磁极面积，在无轴向偏移量情况下，左右两侧磁轴承轴向电磁力相等，飞轮储能系统整机处于平衡位置；当在外界扰动变量影响下，推力盘会偏离平衡位置，向左或者向右运动，从而使得推力盘左右两侧气隙长度发生变化。以推力盘向右运动为例，轴向位移偏移量为Δx，控制电流为i，左右磁轴承电磁力分别为：

此时，飞轮储能系统在左右两侧轴向磁轴承电磁力作用下向左运动回到平衡位置，左右轴向磁轴承产生的回复力F 为：

将左右磁轴承电磁力F1、F2进行泰勒展开取其前三阶，忽略高阶小量，飞轮储能系统磁轴承电磁合力为：

3 飞轮储能系统整机动力学模型

飞轮储能系统在无充放电工况下整机系统处于高速平稳运行状态，当存在外界激励扰动时，系统稳定性被破坏，考虑飞轮储能系统在电动机输出端激励作用下绕某一径向轴转动的运动状态，如图1 所示。

图1 绕y 轴转动飞轮受力分析图Fig.1 Force Analysis Diagram of Flywheel Rotating Around Y-Axis

式中：L—上下磁极面的中心距；D—转子内径。

在电动机输入端激励下，飞轮储能系统运动偏移平衡状态，产生轴向偏移量Δx、径向偏移量Δz，为了探究电动机输入端激励与磁悬浮飞轮储能系统的动力学特性的映射关系，将整机系统结构进行简化，等效为二质体机电耦合模型，如图2 所示。建模时做如下简化假设：忽略飞轮、转子质量分布不均匀的影响，其质心为几何中心；系统无充放电作业时，飞轮储能装置整机处于平稳状态，无径向、轴向偏移；磁悬浮轴承气隙磁场对称分布；忽略漏磁影响。

图2 飞轮储能系统动力学简化模型Fig.2 Dynamic Simplified Model of Flywheel Energy Storage System

飞轮储能系统的动能主要由转子、飞轮转动动能与转子、飞轮偏移引起的平动动能两部分组成：

式中：Ta—飞轮储能系统机构平动动能；Tb—飞轮储能系统机构转动动能；Mi—系统各机构质量；vi—系统各机构平动速度；Ji—系统各机构转动惯量；ω—系统各机构转动角速度；下标1—飞轮参数；下标 2—电机转子参数—飞轮储能系统轴向位移偏移速度—飞轮储能系统径向位移偏移速度。

飞轮储能系统的体系势能：

由泰勒级数可知，飞轮储能系统等效时变刚度系数k（t）在平衡位置δ 附近可以表示为：

飞轮储能系统在轴向运动过程中，转子和飞轮的轴向偏移会造成系统体系的能量消耗，其耗散函数为：

式中：cx—飞轮储能系统轴向运动等效阻尼系数；cz—径向运动等效阻尼系数；cm—电磁阻尼系数。

根据Lagrange-Maxwell 方程建立飞轮储能系统非线性动力学方程，假设系统有N 个自由度，则系统的非线性动力学方程为：

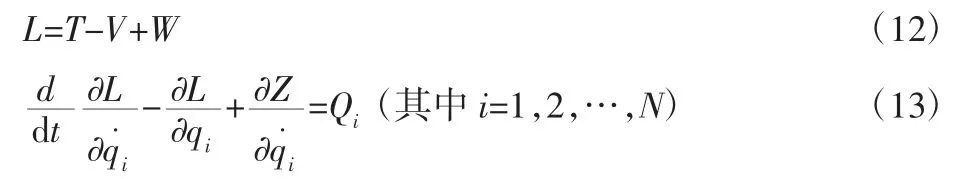
式中：L—Lagrange-Maxwell 函数；T—系统总动能；V—系统总势能；Z—系统的耗散函数；W—电机气隙磁场能；Qi—系统广义坐标的广义力。

将式（7）、式（8）、式（11）带入式（13）求得系统非线性动力学方程：

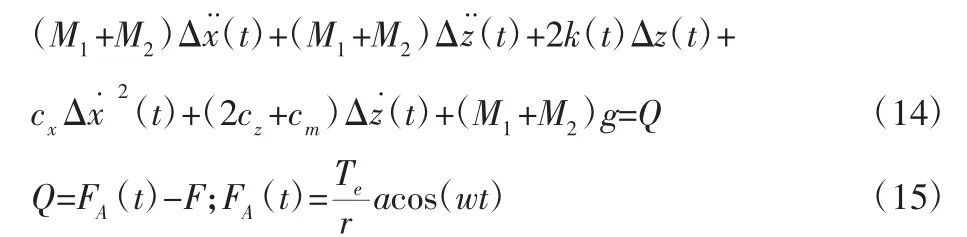
式中：Te—电动机输入扭矩；r—轴径；FA（t）—电动机输入端激励。

将式（15）带入式（14），进行归一化处理，则飞轮储能系统非线性动力学方程可转换为无量纲的形式：

其中，相关参数如下：

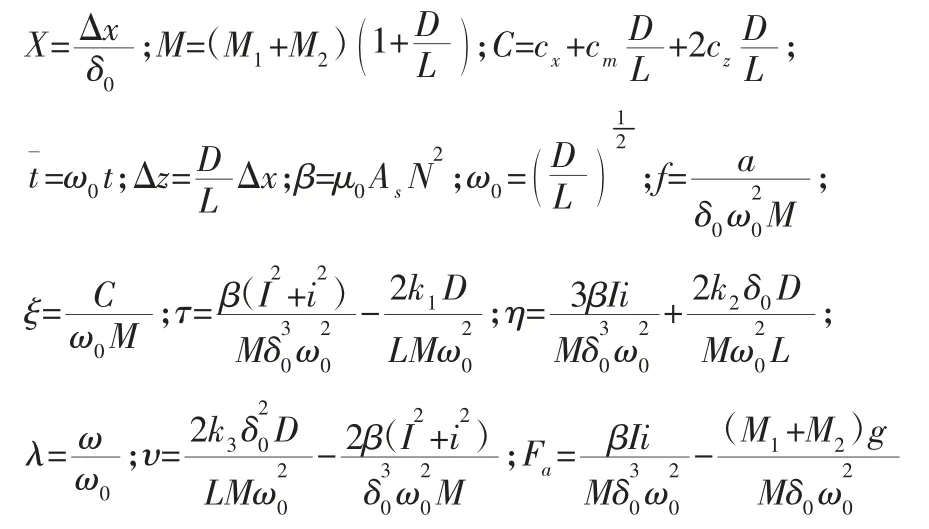
4 数值仿真

为了探究电动机输入端激励对飞轮储能系统机电耦合动力学特征的影响规律，采用Runge-Kutta 法对飞轮储能系统非线性动力学系统进行数值仿真，计算得到时间响应历程曲线、相轨迹图、庞加莱图和幅值谱并进行分析，系统机械和电磁主要参数，如表 1 所示。ξ=0.81，τ=0.3，η=1，ξ=0，υ=0.6，λ=1.2，Fa=0.058，以 f 为控制参数的飞轮储能系统振动系统分岔图，如图3 所示。如图所示，以f 为控制参数时，飞轮储能系统表现出复杂的非线性振动现象，当激励 f 为（0.4～1.11）时，系统为单周期运动；当 f 增大到（1.11～1.1.68）区间，系统运动状态进入两倍周期与四倍周期交替状态；当f 大于1.738 时，系统运动进入混沌运动状态。

表1 系统机械和电磁主要参数表Tab.1 System Mechanical and Electromagnetic Main Parameters Table

图3 控制参数的系统分岔图Fig.3 Bifurcation Diagram Using as Control Paemeter

为了更加直观地分析电动机输入端激励幅值对飞轮储能系统稳定性影响规律，采用三组数值分析系统的运动状态，控制参数分别为f=0.8，f=1.3 和f=1.8，三种不同工况下的时间响应历程曲线、相轨迹图、庞加莱图和幅值谱，如图4～图6 所示。图4 数值计算结果可以看出，当f=0.8 时（激励振幅为78N），其时间历程曲线为简谐运动，系统运动状态为单周期运动；从图5 数值计算结果可以看出，当f=1.3 时（激励振幅为126N），系统运动状态为4周期运动，整机系统发生了倍周期分岔，还未发生混沌运动；从图6 数值计算结果可以看出，当时f=1.8（激励振幅为175N），进入混沌运动区域，时间历程不具备周期性，相轨迹为一系列的交叉环形圈，幅值谱图出现能量集中区域，庞加莱图具有多个孤立点存在，系统进入了混沌运动状态。

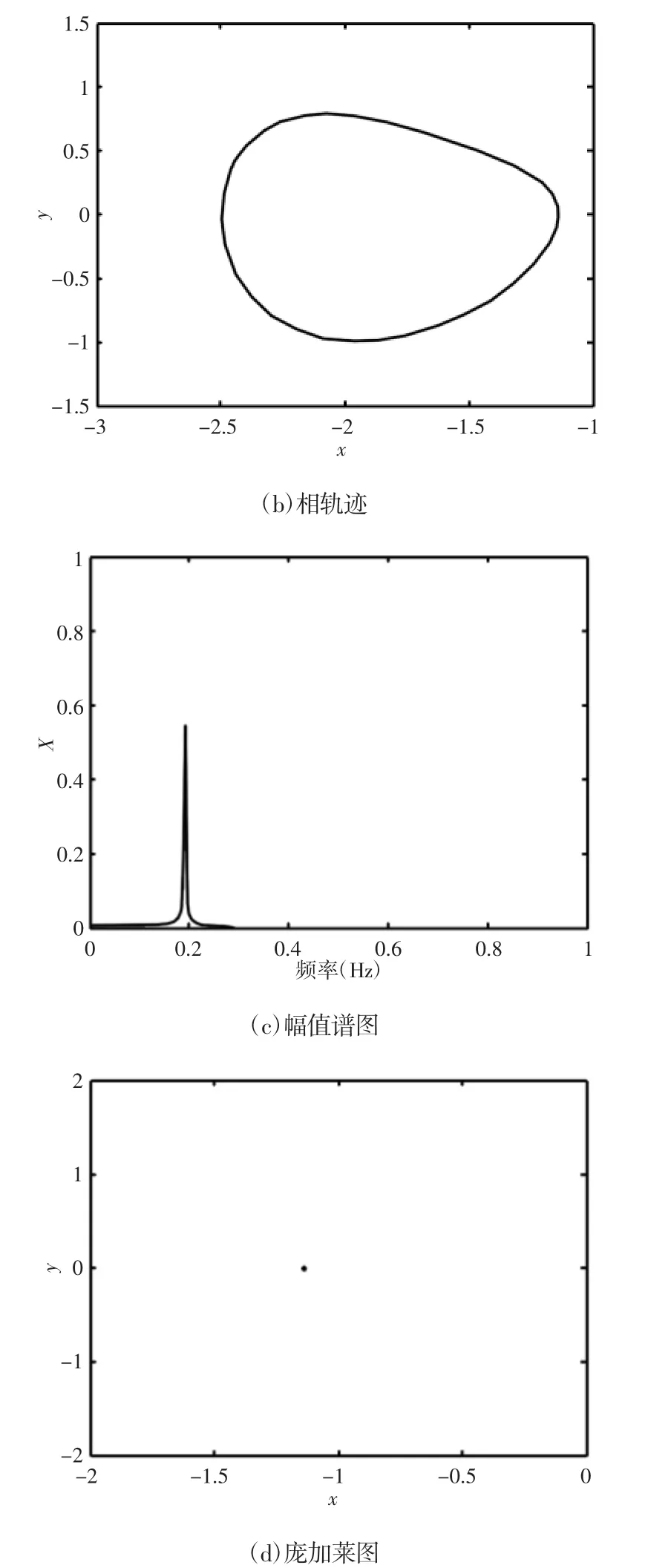
图4 f=0.8 系统混沌运动形态Fig.4 System Chaotic Response for f=0.8

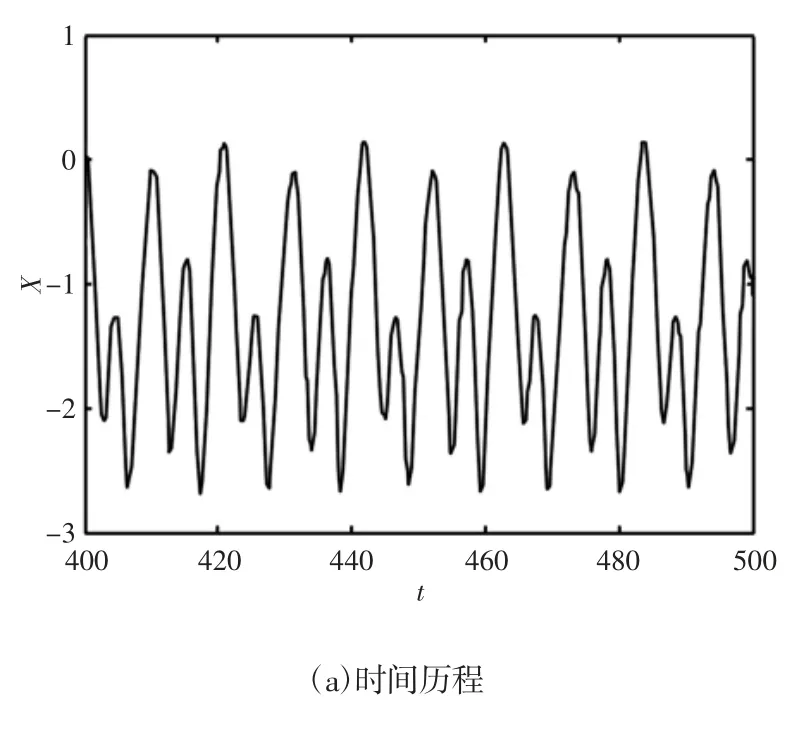
图5 f=1.3 系统混沌运动形态Fig.5 System Chaotic Response for f=1.3

图6 f=1.8 系统混沌运动形态Fig.6 System Chaotic Response for f=1.8

ξ=0.81，τ=0.3，η=1，ξ=0，υ=0.6，f=2，Fa=0.058，以 λ 为控制参数的飞轮储能系统振动系统分岔图，如图7 所示。如图所示，以λ为控制参数时，飞轮储能系统表现出复杂的非线性振动现象，当激励 λ 为（0.4～0.686）时，系统为多周期运动；当 λ 增大到（0.686～1.148）区间，系统为单周期运动状态；当λ 继续增大在（1.148～1.9）区间，系统运动进入混沌和多周期交替状态。同理，为了分析电动机输入端激励频率对飞轮储能系统稳定性影响规律，控制参数分别为λ=1，λ=1.25 和λ=1.7，得到三种不同工况下的时间响应历程曲线、相轨迹图、庞加莱图和幅值谱。当λ=1 时（激励频率为71.8rad/s），其时间历程曲线为简谐运动，系统运动状态为单周期运动，未进入混沌状态，随着激励频率增大，系统开始失去稳定性，可能发生混沌状态；当λ=1.25 时（激励频率为89.75rad/s），系统运动状态从混沌状态进入3 周期运动状态，整机系统发生了倍周期分岔，随着激励频率增大再次进入混沌状态，然后由混沌状态进入2 周期运动状态；当λ=1.7 时（激励频率为122.06rad/s），系统由2 周期运动区域进入混沌运动区域，时间历程不具备周期性，相轨迹为一系列的交叉环形圈，幅值谱图出现能量集中区域，庞加莱图具有多个孤立点存在，系统发生了混沌运动。

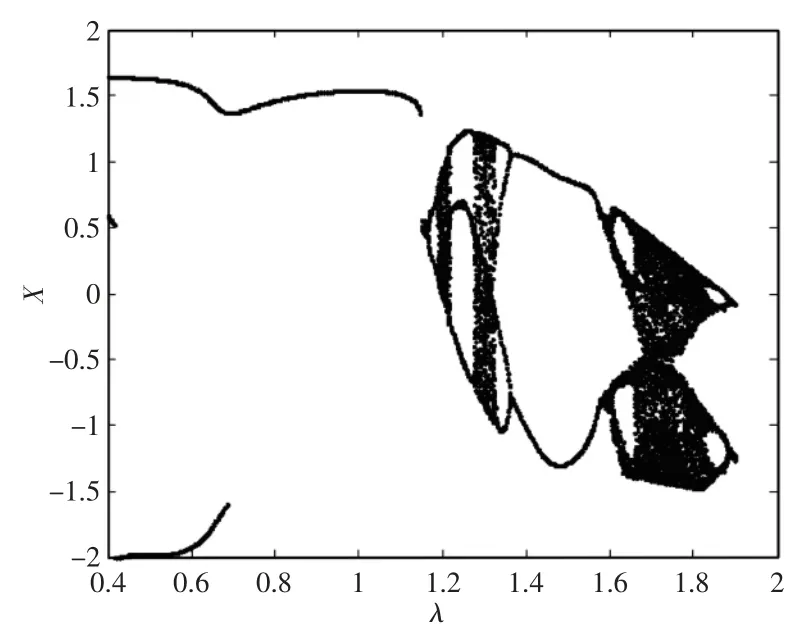
图7 控制参数的系统分岔图Fig.7 Bifurcation Diagram Using as Control Paemeter

5 结论

基于Lagrange-Maxwell 理论建立了飞轮储能系统非线性动力学方程，采用Runge-Kutta 法探究飞轮储能系统在电动机启动瞬间输入端激励作用下的非线性耦合特性，仿真结果表明：（1）磁轴承飞轮储能系统中存在丰富的非线性动力学现象，输入端激励的幅值与频率对系统的运动状态有较大影响，在外部激励作用下，飞轮储能系统运动状态存在单周期运动、倍周期运动以及混沌运动现象，具有明显的非线性特性。（2）当电动机输入端激励幅值较小时，飞轮储能系统为单周期运动，整机运动状态稳定，随着电机输入端幅值的持续增大，飞轮储能系统由单周期运动进入倍周期运动，当幅值大于1.738 时（激励振幅f 大于169.46N），系统开始失去稳定性，进入混沌运动状态。（3）随着电动机输入端激励频率的增大，飞轮储能系统的周期运动（单周期运动和倍周期运动）与混沌运动交替出现，在此范围内，增大或减小激励频率均有可能破坏非线性系统稳定性，造成飞轮储能系统失稳，因此，系统设计参数应尽量避开失稳区域，保证系统稳定性。