旋转机械故障类型识别的神经网络方法研究

2020-11-23孙佳榆杨兆建杨亚东

机械设计与制造 2020年11期

孙佳榆，杨兆建，杨亚东

（1.太原理工大学机械工程学院，山西太原 030024；2.煤矿综采装备山西省重点实验室，山西太原 030024）

1 引言

旋转机械被广泛地应用于各种类型的机械设备中，如提升机、掘进机、风机、蒸汽轮机等等，无论是化工、冶金、矿山、机电等各种工业领域都会应用旋转机械设备[1]。旋转机械设备是否能够安全稳定地运行，对于工业生产显然有着重要的意义。然而，机械设备往往本身构造复杂，故障类型繁多，传统的故障诊断方法已不能满足需求[2]。近年来，故障诊断技术越来越受到重视，各种高新技术被广泛地应用于各种机械设备的故障诊断[3]。人工神经网络以其大规模并行分布式结构，优越的学习能力和泛化能力在机械设备故障诊断中得以广泛应用[4]。

将介绍广义回归神经网络（GRNN）和概率神经网络（PNN）在旋转机械设备故障类型识别方面的研究。同时，将其结果与BP神经网络及RBF 神经网络得到的结果作比较。

2 相关概念与理论

2.1 径向基函数网络

2.1.1 径向基神经元模型

径向基神经元模型，如图1 所示。

其输出表达式为：

式中：radbas—径向基函数，通常为高斯函数：

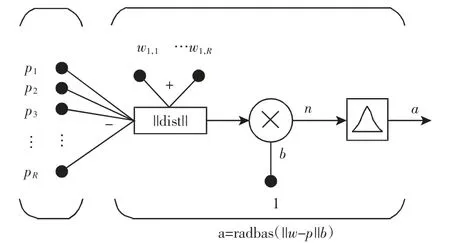
图1 径向基神经元模型Fig.1 Radial Basis Neuron Model

径向基函数的图形和符号，如图2 所示。

径向基传输函数在距离n 为0 时，其输出为1，如图2 所示。在距离n 为0.833 时，输出为0.5。即当输入向量与神经元权值的距离较小时产生的输出值趋于1，从而激活下一层线性神经元的输出[5]。

图2 径向基函数Fig.2 Radial Basis Function

2.1.2 径向基神经网络（RBF）模型

径向基神经网络是一种前向型反向传播网络，它一般有两个网络层：隐含层为径向基层；输出层为线性层，如图3 所示。

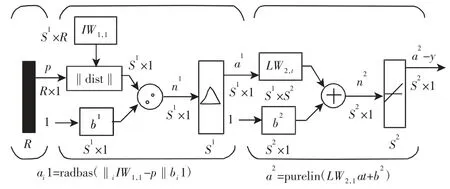
图3 径向基神经网络模型Fig.3 Radial Basis Neural Network Model

网络的输出为：

2.2 广义回归神经网络（GRNN）

广义回归神经网络常常用来实现函数逼近问题。它具有一个有径向基函数的隐含层和一个特殊的线性层。

2.2.1 GRNN 网络结构

GRNN 网络的结构图，如图4 所示。它的隐含层结构与径向基函数网络结构类似，但是输出层的结构不同。

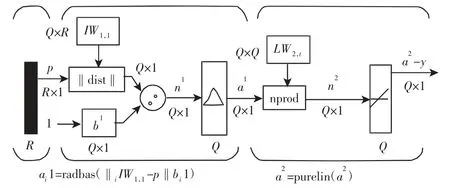
图4 广义回归神经网络模型Fig.4 Generalized Regression Neural Network Model

2.2.2 GRNN 工作原理

GRNN 网络结构中隐含层与径向基函数网络结构基本相同，如图4 所示。输入的样本向量等于其神经元的数目。该神经网络的第一层输入的是输入向量P 和权值向量IW 之间的距离乘以阈值为b1=0.8326/spread 的列向量。Spread 是径向基函数的分布密度。Spread 的大小将极大地影响网络逼近的精度，因此有必要不断调整它的值[5]。

在输出层中，神经元数量同样等于输入的样本向量数，而此时的权重被设置为期望值T。

2.3 概率神经网络（PNN）

概率神经网络结合了径向基函数网络以及经典的概率密度估计原理各自的优点，与传统的前向神经网络相比，更适用于模式分类识别[5]。

2.3.1 PNN 网络结构

PNN 网络的结构图，同样，它的隐含层结构和径向基函数网络结构类似，但是输出层的结构不同，如图5 所示。

图5 概率神经网络模型Fig.5 Probabilistic Neural Network Model

2.3.2 PNN 网络工作原理

概率神经网络的隐含层结构与前两个神经网络的隐含层结构类似，如图5 所示。不同的是，它的输出层通过竞争传递函数（compet）进行选择，将所有类别中概率最大的一类作为输出类别[6]：

3 旋转机械设备故障类型识别

在机械设备的运行环境中，工况条件往往非常复杂，噪声、灰尘等环境因素对振动信号的采集有一定的影响，同时电机电流信号易于采集且受环境影响小。因此，这里选择采用电机电流信号作为故障类型识别的原始信号。

为试验所需电流信号的采集平台，如图6 所示。该平台能够模拟出多种旋转机械常见的故障类型。

图6 旋转机械故障诊断试验平台Fig.6 Rotating Machinery Fault Diagnosis Platform

3.1 数据预处理

在进行故障类型识别前，需要对原始数据进行预处理，提取出故障特征，以便于进行故障类型识别试验。这里采用通过陷波器以及小波包能量提取的方法进行故障特征提取工作[7]。

取正常状态下以及转子碰摩故障、转子角度不对中故障、转子平行不对中三种常见的旋转机械设备故障类别状态下的电机电流信号，进行分段处理。每种类型取50 组，每组2000 个信号点。由于工频信号影响较大，因此对每组信号进行陷波处理，滤去工频信号[8]。再对信号进行4 层小波包分解，提取信号的小波包能量。由于篇幅限制，这里仅展示正常状态下旋转机械电流信号进行陷波处理前后提取的小波包能量图，如图7、图8 所示。

图7 原始信号的小波包能量图Fig.7 Wavelet Packet Energy Map of the Original Signal

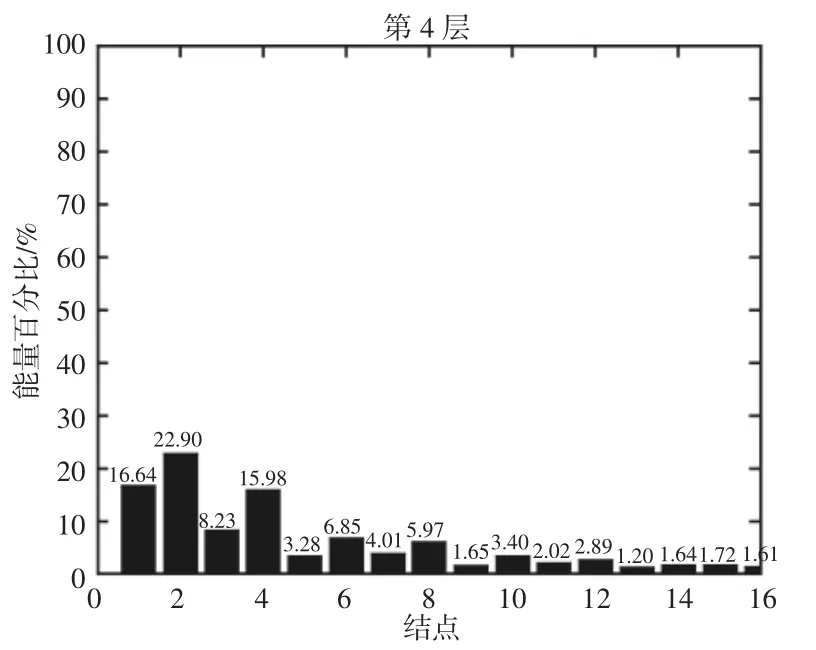
图8 陷波处理后信号的小波包能量图Fig.8 Wavelet Packet Energy Diagram of the Signal After Notch Processing

提取出每组的小波包能量后，得到样本数据的特征向量。部分样本数据的特征向量，如表1 所示。

表1 部分样本数据的特征向量Tab.1 The Feature Vectors of Some Sample Data

其中，类型1 为正常状态数据，类型2 为碰摩故障数据，类型3 为角度不对中故障数据，类型4 为平行不对中故障数据。

3.2 GRNN 神经网络与PNN 神经网络识别

对200 组数据提取小波包能量后，在保证每种故障类型有35 个训练集，15 个测试集的前提下，将得到的数据随机划分测试集与训练集。

建立GRNN 神经网络和PNN 神经网络模型。

循环取遍16 个小波包能量特征的多种组合方式，并建立相应的模型，得到136 个模型后计算每个模型的准确率。

两种神经网络故障类型识别的正确率、运行时间等结果，如图9～图11 所示。

图9 GRNN 神经网络与PNN 神经网络测试结果正确率比较Fig.9 Comparison of Correct Rate Between GRNN Neural Network and PNN Neural Network Test Results

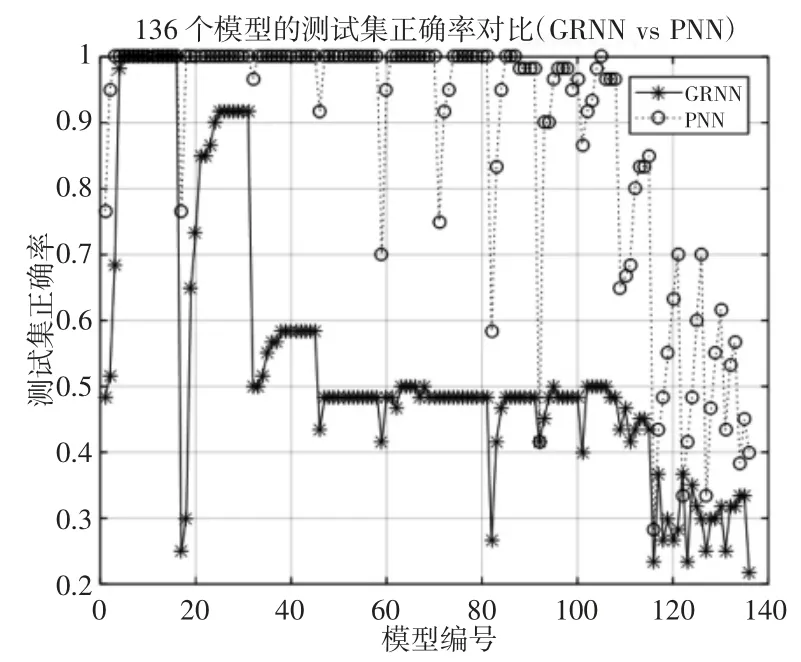
图10 136 个模型的测试集正确率对比Fig.10 Comparison of Test Set Accuracy of 136 Models

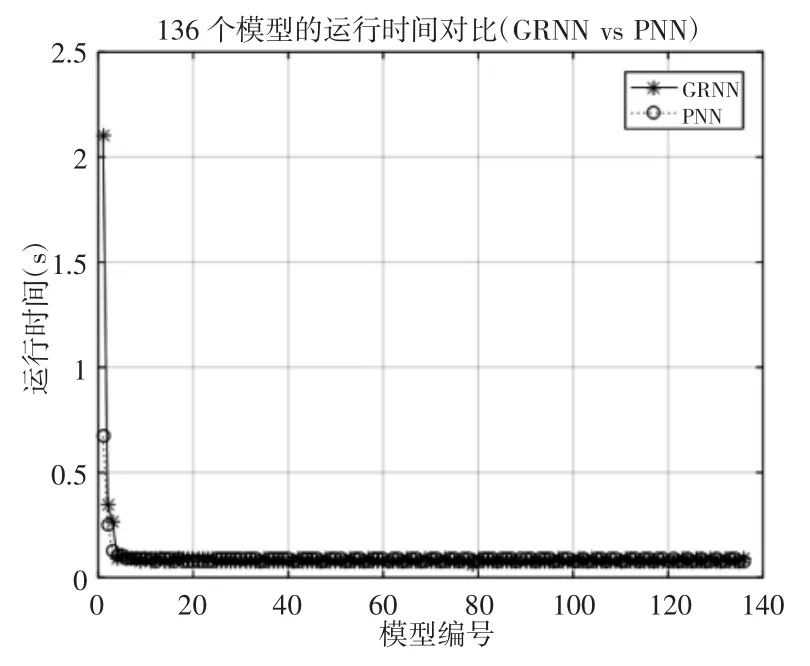
图11 136 个模型的运行时间对比Fig.11 Run Time Comparison of 136 Models

由图9 可见，两者的准确率均为100%，识别效果很好。由图10 可见，在相同的特征组合下，PNN 神经网络的准确率普遍高于GRNN 神经网络，即相对于GRNN 来说，PNN 可以在更少的特征条件下识别出正确的故障类型。由图11 可见，两种神经网络在开始时花费时间差距较大，GRNN 相比PNN 花费了更多时间，在之后的模型中，两者花费的时间几乎相等。

3.3 BP 神经网络与RBF 神经网络识别

在BP 神经网络和RBF 神经网络分类识别中，也应用上述预处理后得到的小波包能量特征数据。对所得数据划分训练集和测试集后，进行归一化处理。

3.3.1 BP 神经网络识别

输入训练样本后，建立BP 网络模型。设置训练参数，最大步数设为1000，训练目标设为1e-3，学习率设为0.01。BP 神经网络训练过程，用7 步就达到了训练目标，如图12 所示。

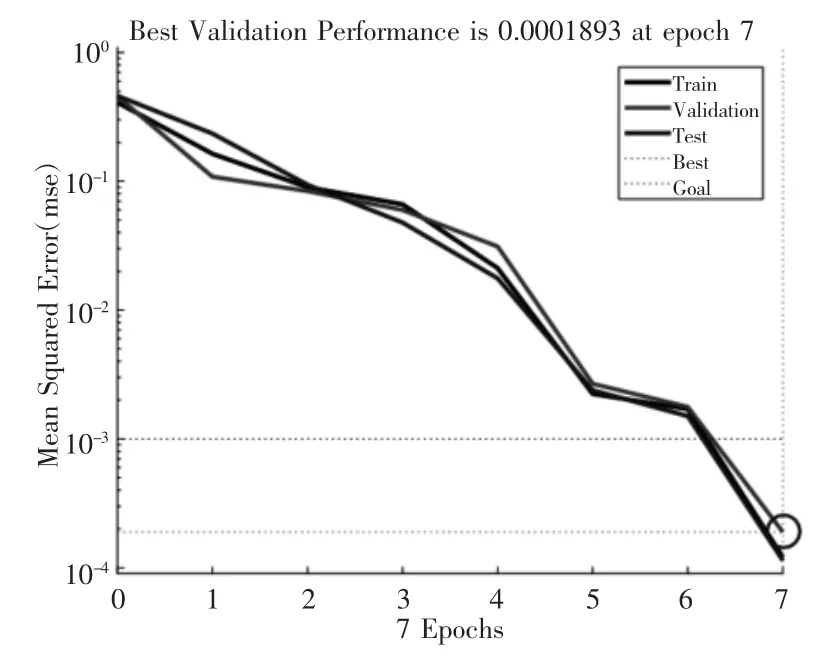
图12 BP 神经网络训练过程Fig.12 BP Neural Network Training Process

对训练好的网络进行仿真测试后，将得到的结果用round 函数取整。由于BP 神经网络不稳定性，这里取5 次预测结果计算其平均值，作为其最终结果。

结果显示，BP 神经网络平均1 组数据识别错误，其余均识别正确，识别准确率为98.33%。

3.3.2 RBF 神经网络识别

RBF 网络是一种前向网络的拓扑结构[9]。参数spread 取30。将数据随机划分测试集与训练集后进行归一化处理，输入RBF神经网络模型中，同样用round 函数取整，取5 次结果计算其平均值。

结果显示，RBF 神经网络平均2 组数据识别错误，其余均正确，识别准确率为96.67%。为其中一次识别时，真实值与预测值识别的结果对比，如图13 所示。

图13 RBF 神经网络故障类型识别结果Fig.13 RBF Neural Network Fault Type Identification Result

4 四种神经网络的比较

综合上述结果，各个神经网络识别的准确率，如表2 所示。可以看到，按照识别准确率以及鲁棒性来看，GRNN 和PNN 神经网络均优于BP 和RBF 神经网络。而在识别时间和特征选择上PNN 又优于GRNN 神经网络。因此，可以得到，在此次旋转机械故障类型识别试验中PNN 神经网络为最佳选择。这与其在模式分类识别上的优势相符。