面向高效的并行拆卸序列优化方法

2020-11-23阚欢迎田晓飞张文胜

机械设计与制造 2020年11期

张雷，阚欢迎，田晓飞，张文胜

（1.合肥工业大学机械工程学院，安徽合肥 230009；2.中国质量认证中心，北京 100000）

1 引言

机械产品在再制造和维修回收过程需要对构件和零件进行拆卸，产品拆卸[1]是在一定规则约束下进行的零部件分离行为。在拆卸过程中记录零部件分离顺序的序列称为拆卸序列，而拆卸序列规划就是在提高产品拆卸效率，降低拆卸成本等各项要求的前提下挑选出的最优序列。在产品拆卸方面，主要包括串行拆卸和并行拆卸[2]。目前，串行拆卸序列规划方法主要包括以图论为基础的紧固件图[3]、AND/OR 图[4]、混合图模型[5]等方法，但随着产品结构的复杂化，激增的零件数量致使传统的拆卸方法无法解决复杂产品拆卸序列规划的问题，因此众多学者选择改进的人工智能算法解决产品复杂化出现的组合爆炸问题，文献[6]构建了拆卸Petri网模型，通过混沌粒子群优化算法解决了拆卸序列规划；文献[7]提出了可行度及自适应算法优化人工蜂群算法，极大提高了拆卸序列收敛的速度及求解质量。

随着产品的复杂程度的增加和企业对拆卸效率的提高，并行拆卸与串行拆卸相比，能提高拆卸效率。文献[8]利用模块设计理论对复杂产品进行并行化分析，并提出五项原则指导选择性并行拆卸规划的求解，但该方法适用面有限，易受产品结构约束。文献[9]提出并行序列染色体编码方法，并加入不可行惩罚因子实现并行拆卸序列的优化，但因其拆卸模型求解效率较低，零件选取顺序随机性太强，导致求解质量一般。文献[10]通过基于模糊等价关系的动态聚类方法实现了拆卸作业的并行化，但聚类模块间的连接零件集合难以求解，增加了并行规划求解的复杂性。

综上所述，为了解决复杂产品在并行拆卸序列规划问题求解时存在求解模型过于冗杂、求解质量较差等问题。应用序列矩阵方法解决并行拆卸序列长度及步长难以描述的问题；根据并行拆卸特点提出了拆卸单元选取原则，建立了并行拆卸最少耗时优化模型，并结合人工蜂群算法，提出了诱导因子算法，实现了并行拆卸序列规划问题的快速、高质量的求解。

2 拆卸混合图的描述

拆卸混合图描述了各个零件之间的约束关系，可被定义为：G=｛V，E，DE｝。其中，V=｛v1，v2，…，vn｝为顶点，表示基本拆卸单元，n 为基本拆卸单元的总数。E=｛E1，E2，…，Eo｝为无向边，代表两个基本拆卸单元之间存在接触连接关系，用实线表示，o 为无向边的条数；DE=｛DE1，DE2，…，DEl｝为有向边，代表两个基本拆卸单元之间存在优先约束关系，用带箭头的实线表示，箭头方向由约束零件指向被约束零件，l 为有向边的条数。某结构示意图，如图1 所示。拆卸混合，如图 2 所示。此时 n=10，o=9，l=10。

图1 结构示意图Fig.1 Schematic Diagram of a Structure

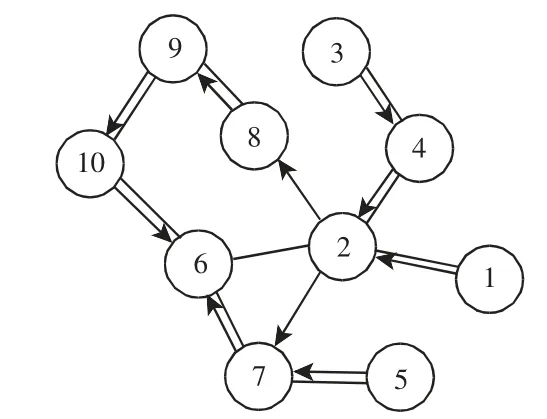
图2 拆卸混合图Fig.2 Disassembly Hybrid Graph

根据拆解单元之间的连接关系与优先关系，连接矩阵Gc和优先约束矩阵Gp可由拆卸混合图G 可以推导出，即：

当 i=j 时，Pij=0

部件4 在拆卸之前必须优先拆卸部件3，两者之前存在优先约束关系，用带箭头的实线表示，由3 指向4，如图1 所示。且两者之间又存在连接关系，用无箭头实线表示。由此可以得出此结构的拆卸混合图，如图2 所示。

3 并行拆卸序列规划的关键问题

并行拆卸是对拆卸任务的进行并行化处理从而缩短拆卸序列串行长度，进而减少拆卸时间。在保证所有拆卸单元可拆性的基础上，在并行拆卸序列过程中为了缩短拆卸序列长度采用多单元同步拆卸方法。为了消除在并行拆卸序列规划中存在的问题，研究了可变序列矩阵的建立方法和并行拆卸单元选取方法。

3.1 可变序列矩阵的建立

一般情况下，产品的基本拆卸单元数量是可知的，根据零件之间的约束关系，可以轻松的计算出串行拆卸序列的步长和长度，并且可以采用单一集合模型对其进行表示。然而，在并行拆卸中不能采用单一集合模型对拆卸步长和序列长度进行表示，主要原因有以下几点：（1）在产品拆卸的过程中受到拆卸环境和拆卸单元约束的影响；（2）拆卸步长不完全一致；（3）拆卸并行度与每个拆卸步骤的拆卸步长可能不一致。

为了解决上述问题，采用可变序列矩阵方法，来描述并行拆卸序列问题。序列X：｛X1，X2…Xg｝表示含有有g 个拆卸基本单元串行拆卸序列，我们可以把该串行序列看作并行度为1，步骤数为g 的并行拆卸序列。以此类推，序列P 为ir 行ic 列的矩阵，表示其包含ir*ic 个拆卸基本单元，步骤数为ir，并行度为ic 的并行拆卸序列，即P 为：

式中：P—并行拆卸过程中可变序列矩阵，并行拆卸的步骤数与矩阵最大行数数值上相同，即mmax，同样地，拆卸并行度和矩阵最大列数相同，即Emax，因此产品的拆卸单元可以表示为P（ir，ic）。

在可变序列矩阵中每个元素代表一个拆卸单元，在每行中各元素为并列关系且属于同一拆卸步骤。当该步骤中拆卸并行度数大于拆卸单元数，将同行中缺少的元素设置为0；矩阵中的一行代表一个拆卸步骤，故行数即为拆卸步骤数。

例如图1 所示结构，若并行拆卸度为2，拆卸步骤总数为7并行拆卸顺序如下：（3，5→1，4→2→7，8→9→10→6）。则可用 7*2的并行拆卸序列矩阵P 表示：

由此可见，并行拆卸序列可以通过并行拆卸序列矩阵进行描述，同时在可变序列矩阵的逐行构建过程中，能解决并行拆卸序列长度与拆卸步长相互影响变化的求解问题。相应的流程如下：

首先为了便于操作，m 表示总单元数，n 表示拆卸序列中第n 个元素，Vn表示第n 个元素所代表的拆卸单元，Emax表示拆卸并行度。Q 为判断变量，Te 表示中间变量。

（1）初始化。

在拆卸开始时，取步骤数k=1，单元数Ek=0，序列矩阵P（k，：）=0，n=1；

（2）可拆卸性检验。

若是，则令 Ek=Ek+1，Te=Dk，序列矩阵 P（k，Te）=Vn，n=n+1；

若否，且Ek=0，则跳转到（5）；

若否，且 Ek＞0，则 Te=Emax；

（3）若n=m+1，则循环结束，转到（5）；否则返回（2）；

（4）若Te=Emax则删除P（k，：）中各单元的约束和连接关系，且 k-k+1，Ek=0；

（5）输出结果。

如果n＜m+1，表明该拆卸序列无法进行并行拆卸，此时Q 为0。n 表示不可拆性单元的序号。如果n=m+1，表明满足并行拆卸，此时Q 为1，k 为拆卸步骤数，拆卸单元记录在P 中，为基本单元数量。Ek如图 1 所示模型，串行拆卸序列可以表示为｛3，5，1，4，2，8，7，9，10，6｝，通过上述算法可得图 1 也可以进行并行拆卸，拆卸并行度为3，且可变序列矩阵P 为：

其中拆卸步骤数 kmax=7，对应步长分别为（3，1，1，2，1，1），并行拆卸顺序为：1，3，5→4→2→7，8→9→10→6 因此，通过可变序列矩阵算法可将串行序列转化为并行拆卸序列。

3.2 并行拆卸单元选取方法

独立存在性是并行拆卸中各拆卸单元拆卸时间显著的特点，在并行拆卸确定拆卸顺序的同时，应满足整体拆卸序列并行程度最大化原则，由于需要考虑多种因素致使拆卸序列的确定变得尤为复杂，大大增加了并行拆卸序列建立的困难程度。

如果在拆卸过程中拆卸并行度大于可拆卸单元数量，要满足步骤数最小化原则进而实现整个并行拆卸序列的并行程度最高。在选取拆卸单元时，采用基本拆卸时间和拆卸约束能力来解可拆卸单元数量大于拆卸并行度的问题，单元拆卸约束能力即：

式中：j—优先约束的单元个数；Z（j）—单元拆卸约束能力。

在进行并行拆卸序列规划时，拆卸单元的被约束关系应最大程度的释放，增加可拆卸单元数量；同时在拆卸过程中应优先对Z（j）值最大的单元进行拆卸。在图1 所示的结构中，若拆卸并行度为 2，单元 1，3，5 都可被拆卸，对应的拆卸约束能力 Z（j）可分别表示为 6，7，2，其中单元 3 的 Z（j）值为 7 应优先被拆除，这样单元4 就可以被释放出来，从而在第二个步骤中就可对单元4进行拆卸，对应的拆卸顺序可表示为：（1，3→4，5），其拆卸步骤数为2；否则拆卸顺序可表示为：（1，5→3→4），其拆卸步骤数为3。

时间相关性是并行拆卸的显著特点，拆卸单元中耗时最长的拆卸单元决定了该步骤的拆卸时间，因此在整个拆卸过程中拆卸工位闲置现象就会出现在那些远小于最大拆卸时长的单元上，违背了提高并行拆卸效率的原则。因此为了避免工位闲置现象，除了遵循可拆性和整体步骤数最小的原则外，还应考虑一种特殊的情况，即当拆卸并行度小于可拆卸单元数时，应优先考虑Z（j）值较大的单元，并选择与其拆卸时长相近的单元优先进行拆卸。

4 拆卸序列优化模型的建立

4.1 拆卸单元的可拆卸性判别

拆卸单元的可拆性是求解并行拆卸序列规划问题的前提条件，即当前拆卸单元没有受到其他单元的优先约束且只含有单一的连接关系。故记：

式中：S（i）—基本拆卸单元i 在被拆卸前需要优先拆卸的单元个数；W（i）—与基本拆卸单元i 存在连接关系的单元个数。所以基本拆卸单元的可拆卸性要同时满足式（2）～式（3）。

4.2 优化目标函数的构建

与串行拆卸不同，在并行拆卸过程中如果若干个单元的同步拆卸为一个步骤，此时该步骤的拆卸时长由此步骤中耗时最长的单元决定。若在并行拆卸中第k 个步骤的拆卸时长记为tk，根据并行拆卸序列的总时长的定义，则有：

式中：T（x）—并行拆卸序列x 的拆卸总时间。因此并行拆卸序列的总时长优化模型为：

5 基于带诱导因子人工蜂群算法的并行拆卸序列规划

为解决多约束组合优化问题的求解，在2005 年土耳其学者文献[11]提出人工蜂群算法（artificial bee colony，ABC），该算法操作简单、精度高和稳定性强的特点被充分体现，目前也在拆卸规划的求解中得到应用[7，10]。为了便于对拆卸序列规划问题进行求解，首先通过前文算法对串行拆解序列并行化处理，然后再对人工蜂群算法进行初始化。为了解决并行拆卸序列的快速收敛的问题，结合并行拆卸序列规划的特点，以前文拆卸序列单元选取的原则为基础，提出了一种带诱导因子的蜂群算法。通常我们把第m 个拆卸步骤中此时拆卸约束能力最强的单元imax（j≠imax）和拆卸单元i 的拆卸时长之差的绝对值，即，称为诱导因子。当t（mimax，j）越小，则表明单元j 比其他的单元拆卸优先级低。并行拆卸序列规划步骤如下：

（1）初始化。随机生成初始拆卸序列Xt（t=1，2，3，…，MP），其中MP 为初始种群数量。每个拆卸序列Xt包含m 个零件。

（2）新序列生成。Xm和Xr分别为引领蜂m 和r 对应的序列（其中r≠m），在两个序列中随机选择两个元素进行交换（其中r≠m），新的拆卸序列由此产生。当Xm的适应度高于新的拆卸序列的适应度时，则保留原值，否则Xm将被替代。同时更新相关数据。适应度根据式（6）计算。

当序列x 可进行并行拆卸时，P=1，此时：

当序列x 无法并行化时，P=0，此时的fitx为0，其值比前者小，因此新生成的序列替代将代替旧拆卸序列。

（3）计算转移概率。根据式（8）计算。

（4）结合诱导因子新序列的生成。当序列确定以后，根据诱导因子算法决定拆卸序列中需要交换的元素，并更新相关数据。

（5）新序列优良性的判断，如果不满足条件，则放弃原序列，转至（1）继续搜寻。

（6）终止条件的判定。若不满足条件，则转至（2）继续进行搜寻；若满足条件，则结束循环。

6 实例分析

采用MATLAB 软件编写并行拆卸算法，选取某型号发动机验证上述算法，发动机模型，如图3 所示。将模型分为32 个拆卸单元，并对拆卸单元进行编号生成拆卸单元信息表，如表1 所示。根据零件和拆卸单元之间的约束关系生成拆卸混合图，如图4 所示。

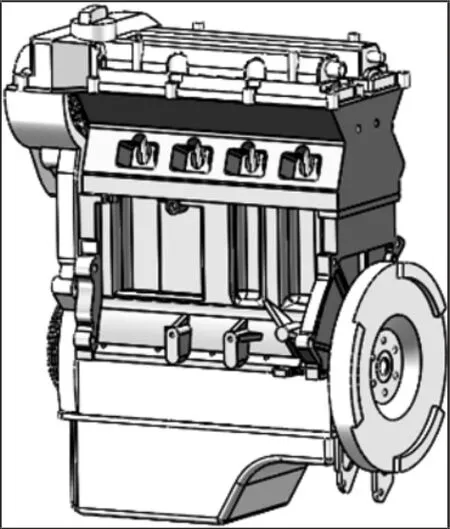
图3 发动机模型Fig.3 The Model of Engine

表1 拆卸单元信息表Tab.1 Information Table of Disassembly Unit

图4 拆卸混合图Fig.4 Disassembly Hybrid Graph

改进的人工蜂群算法的参数设置如下：初始种群数量为100，迭代次数为500，单个寻优目标最大迭代次数为200，当Emax为 2 时，最优并行拆卸序列为：16，20→11，18→12，15→19，6→21，22 →1，17 →24，25 →13，2 →10，5 →9，4 →23，14 →3，8 →26，32→27，31→28，29→30。最大拆卸步骤数 Kmax为 17 步，最短的拆卸时间为1054s。当拆卸并行度Dmax为3 时，其最优并行序列为：16，20，6 →11，18，12 →5，10，19 →13，21，22 →1，9，17 →4，24，25→2，15→14，23→3，8，26→27，32→28，29，31→30→7，最大拆卸步骤数Kmax为13 步，最短的拆卸时间为882s。通过上述分析发现适当提高拆卸并行度，可获得较为优异的拆卸序列，提高拆卸效率。

当选用文献[11]中的算法对发动机模型拆卸序列进行规划师，可以得出最优并行拆卸序列为：1，23→16，20→11，18→12，15→14，17 →19，6 →21，22 →24，25 →13，2 →9，4 →3，8 →26，32 →27，31→28，29→30→7，最大拆卸步骤数 Kmax为 17 步，最短拆卸时间为1067s。两者对比图，如图5 所示。

图5 对比图Fig.5 Comparison Diagram

从对比图来看，这里算法收敛迭代次数比文献算法少，而且曲线的阶梯转变次数明显大于文献算法，因此所用的方法能够更好地处理复杂模型的并行拆卸序列规划问题。根据两种算法的拆卸序列可以看出在1，14，17 等拆卸单元的拆卸序列规划时存在明显的差异，在并行拆卸序列构建的开始阶段，将单元16 和20 作为起始拆卸步骤，而文献算法将单元1 和23 作为并行拆卸系列的第一步。由于提出的算法能释放约束能力较强的拆卸单元，为拆卸单元的选取提供理论支持，缩短了拆卸时间，提高了拆卸效率。