基于嵌入干扰机制的改进人工鱼群算法及其应用

陆凤仪，任 重，徐格宁

（太原科技大学机械工程学院，山西 太原 030024）

1 引言

人工鱼群算法（AFSA）[1-2]作为一种基于动物自治体的寻优模式，具有适应性、自制性、盲目性、突现性、并行性特点，其鲁棒性强、全局收敛性好、对初值要求低，但也存在后期收敛速度慢、寻优精度不高[3]、早熟现象[4]等缺陷。因此，国内外学者针对上述问题相继提出了各种改进人工鱼群算法。其中，文献[5]中提出了基于粒子群算法的人工鱼群算法，改进了聚群和追尾行为中的随机移动算子，提高了求解精度，但在稳定性方面并没有证明是否得到改进；文献[6]提出了基于模拟退火算法改进的人工鱼群算法；将判断准则引入到觅食行为中，通过多峰测试函数与病态单峰测试函数证明提高了求解精度，但人工鱼群算法属于早熟算法，文中所述的提高了后期收敛速度并没有证明；文献[7]提出了采用动态调整人工鱼视野和步长的方法，在局部更新采用阀值选择策略，建立了适用于水库群优化调度的人工鱼群算法，但该改进使用范围有限，不适用于其他行业；文献[8]中提出了PID 控制的参数寻优，应用PSO、GA、SA、自定义初始种群插入人工鱼群算法中，模拟了PID 参数人工设置，提高了算法的运算速率和精度，但在算法稳定性方面未提出改进。

上述改进多数针对某一缺陷，而未涉及算法中参数之间相互关系及早熟现象，为探究AFSA 中视野与步长的相互关系，以参数统计分析为基础，设定步长与视野数值成反比的条件下，构建一种模仿生物视觉特性的步长、视野因子模型。为减缓人工鱼群算法中的早熟现象，使算法在迭代后期仍会朝着目标值无限接近，将差分进化算法中的变异行为作为人工鱼群完成觅食、聚群、追尾行为后的干扰行为，通过测试函数验证其收敛性、计算精度、稳定性。桥式起重机广泛应用于工矿企业中，箱型主梁作为主要承载构件，占桥式起重机总重的60%以上。在传统设计中箱型梁截面尺寸常根据设计人员工作经验或起重机设计手册进行选择[9]，为减小主梁自重，降低生产成本，现多采用智能优化方法设计。为验证这类算法的实用性，将应用于50t/22.5m 桥式起重机主梁金属结构轻量化设计。

2 人工鱼群基本算法

一片水域中的鱼群能够通过侧向反馈机制觅食，鱼生存数目最多处一般为该水域中营养物质最丰富处。人工鱼群算法根据这一现象，通过构造人工鱼来模拟鱼群的觅食、聚群、追尾行为，达到寻优目标。以下为人工鱼群算法的几种典型行为：

（1）觅食行为（AF_prey）：设人工鱼当前状态为 Xi，在其视野范围内随机选择一个状态Xj（即di，j≤Visual），若对应的食物浓度Yi＞Yj（极小值问题），则向该方向前进一步；反之重新选择随机状态Xi，反复试探Tn次后若仍不满足前进条件，则随机前进一步[1]。

可描述为：

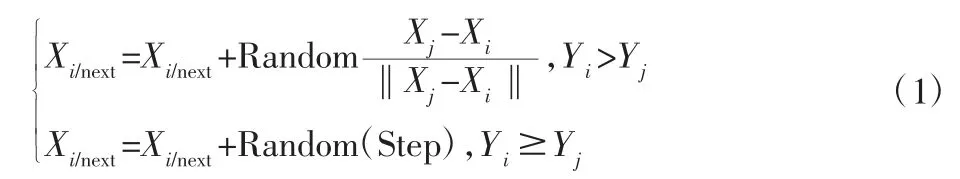
式中：Yj—状态Xi对应的食物浓度；Xi/next—第i 条人工鱼的状态；Random（Step）—［0，Step］间的随机数工鱼个体之间的距离。

（2）聚群行为（AF_swarm）：设人工鱼当前状态为Xi，搜索其临域内（即 di，j≤Visual）的伙伴数目 nf和中心位置 Xc，若对应的食物浓度Yc/nf＞δYi（伙伴中心具有较多食物，且不太拥挤），则向伙伴中心Xc移动一步，否则执行觅食行为[1]。

可描述为：

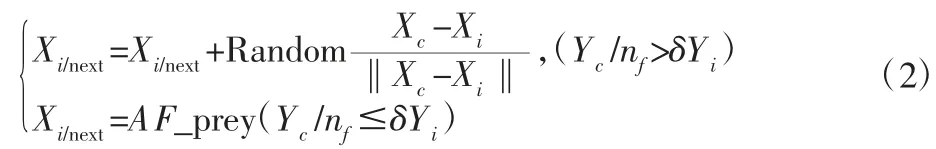
（3）追尾行为（AF_follow）：设当前人工鱼状态为 Xi，搜索其临域内（即 di，j≤Visual）伙伴中 Yj为最大的 Xj，且满足 Yc/nf＞δYi（伙伴Xj具有较多食物，且不太拥挤），Xi临域内伙伴数目nf为则朝伙伴Xj前进一步，否则执行觅食行为[1]。

可描述为：

（4）随机行为（AF_random）：人工鱼在视野范围内随机选择一个状态，然后向其移动，以便更大范围内寻觅食物或伙伴，该行为为觅食行为的缺省行为[1]。

3 算法改进

3.1 对人工鱼群步长与视野的改进

人工鱼群搜索范围的大小与视野有关，收敛速度和寻优精度与步长有关[3]，为研究视野与步长的关系，需获取不同步长对应的最佳视野值，如图1 所示。根据生物视觉的特性，随着移动速度的增加，生物视野水平逐渐变窄，视野度数逐渐减小，因此设定视野与步长成反比，为判断其是否存在相关关系，通过式（4）采用统计方法对参数进行分析。

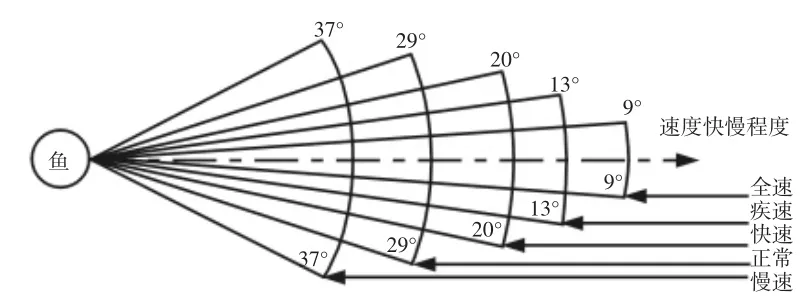
图1 生物视觉特性图Fig.1 Biological Visual Characteristics

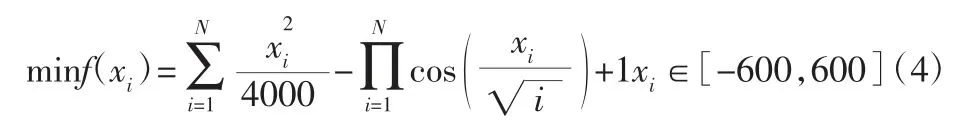
算法在MATLAB 中运行，参数设置：fishnums=100、MAXGEN=500、delta=0.6、try_number=1，Visual 值变化范围（1～9）（步进为1），Step 值变化范围（1～9）（步进为 1）采用排列组合的方式对Visual、Step 值进行组合，分别对式（4）进行 20 次试验，将每组Step 所对应的最优Visual 值记录结果，如表1 所示。当迭代次数为500 次时，最优值表示解决方案，平均值表示20 次试验中平均最优值。

表1 对 Visual、Step 的测试数据Tab.1 Test Data for Visual and Step

通过MATLAB 对表中Visual、Step 值进行拟合，结果如图2所示。

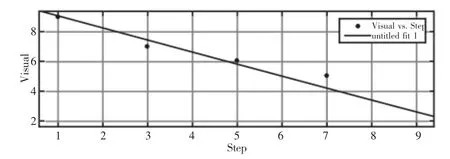
图2 对Step、Visual 测试数据拟合结果Fig.2 Fitting Results of Step and Visual Test Data

根据拟合结果显示，Visual 与Step 成反比关系，可提出关系式为：

其中：p1=-0.8（-1.118，-0.4818）且 p2=9.8（7.972，11.63）。

采用其得出的与值在一定范围内可以提高寻优精度。

3.2 算法行为改进

鱼的社会行为级别不高，无分工和地位的差异。因此当鱼群分散觅食时，若一条鱼发现了目标，鱼群便会产生群体间的依赖性，对周围食物产生漠视，直到将最先发现的食物消灭干净，才会继续寻找其它的食物。这种群体间的行为导致人工鱼群算法陷入局部最优的几率增大，同时在搜索过程中，人工鱼群会出现“早熟收敛”现象[10]，所以在原有行为基础上嵌入基于差分进化算法中的变异过程作为干扰行为，相比于遗传算法中的变异过程，差分进化算法[11]中的变异过程可控性更强，随机性较小，其变异范围限制在不同个体鱼之间，而不是在变量范围内随机生成一个或几个变量。当鱼群完成追尾行为之后对其实施干扰，增加跳出局部最优解的概率，缩短寻找全局最优解的时间，其数学形式为[12]：

DAFSA 结构流程图，如图3 所示。具体步骤如下：

（1）根据给定的变量范围、鱼群大小，选择算法参数，随机生成初始种群；

（2）计算每条人工鱼的目标函数值，执行聚群、追尾（觅食、随机）行为，分别生成新个体；计算新个体的目标函数值，并判断二者大小，选择最小的个体并替换至原种群中对应的位置；

（3）判断新个体是否满足变量条件，如不满足则取相对应变量的上下限替代原有值；

（4）对新生成的个体实施干扰行为，使种群扩大搜索范围；

（5）判断是否满足迭代要求，如不满足则继续执行步骤（2），如满足则跳出循环，输出结果。

图3 改进人工鱼群算法流程图Fig.3 Flow Chart of Improved Artificial Fish Swarm Algorithm

为验证DAFSA 算法是否满足在稳定性、计算精度以及后期迭代是否朝着目标值无限接近的改进要求，从文献[13]中选取5 种不同类型测试函数进行测试，测试函数，如表2 所示。

起重机箱型梁截面尺寸优化方程为非线性复杂函数，部分变量具有较大搜索空间，因约束条件较多，其搜索方向难辨，所以综合考虑选用以上5 种测试函数，如表2 所示。

算法在MATLAB 中运行，参数设置，如表3 所示。

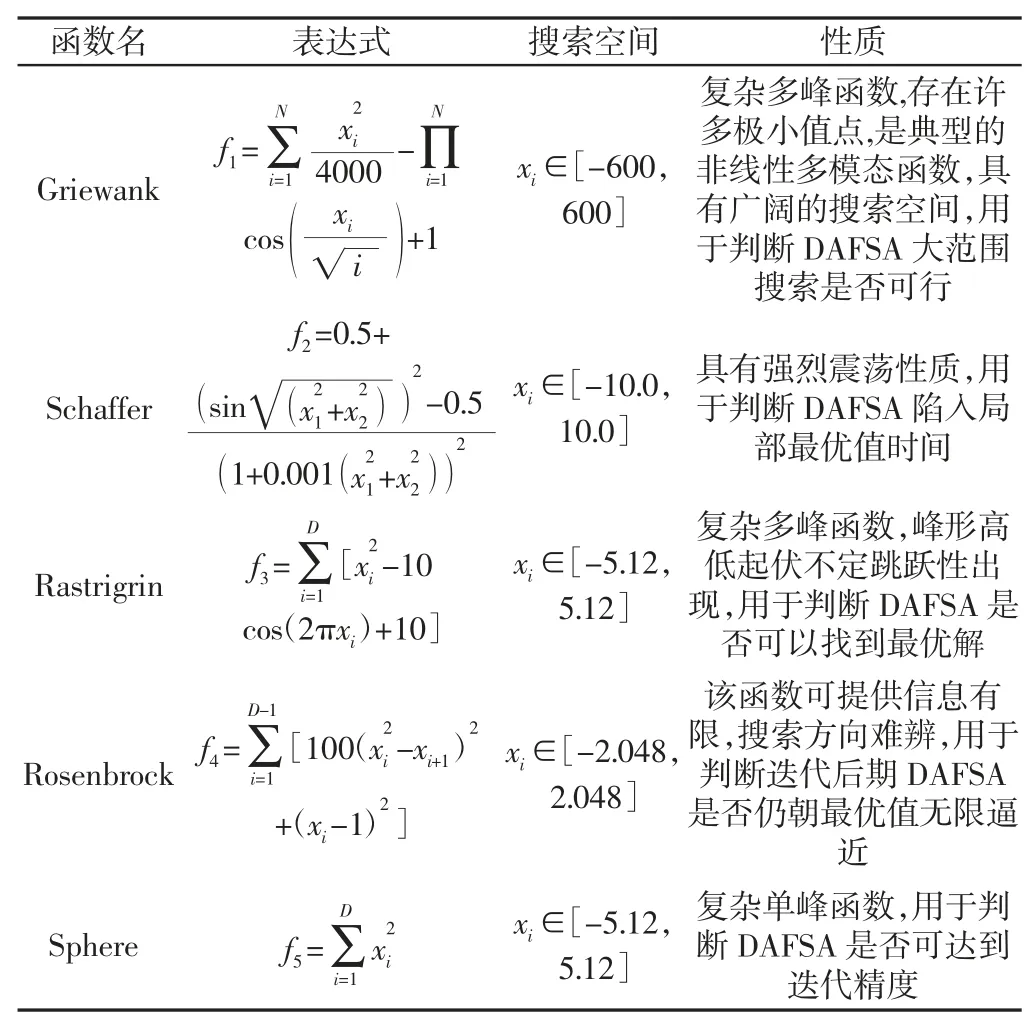
表2 5 种不同类型测试函数Tab.2 5 Different Types of Test Functions

表3 运行参数设置Tab.3 Running Parameter Settings

对每个测试函数按照AFSA、DE、DAFSA 三种不同算法分别运行20 次，结果如表4 所示。其中平均值表示20 次测试中平均最优值，最优值表示解决方案，标准差值表示该算法的稳定性，时间表示该算法获得20 次解所需平均时间。

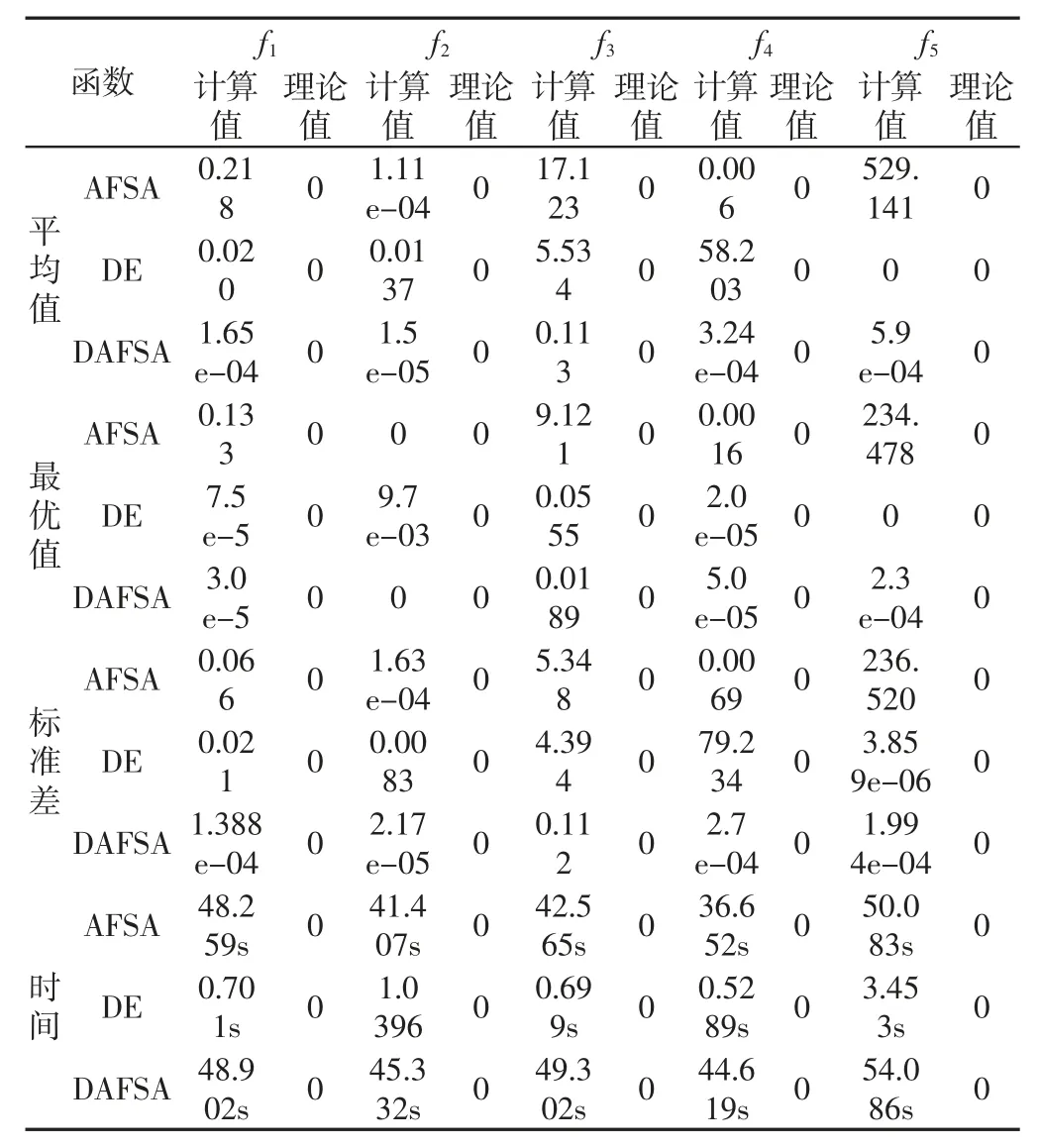
表4 测试结果Tab.4 Test Results

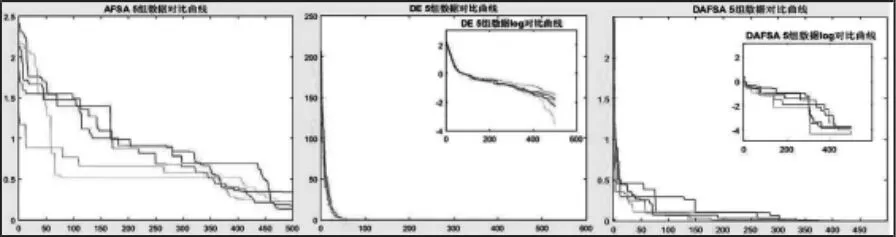
图4 三种算法对测试函数f1 迭代过程对比图Fig.4 Comparison Diagram of Three Algorithms on the Iterative Process of Test Function f1

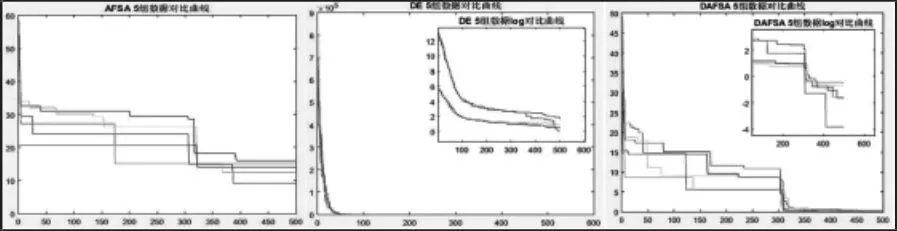
图5 三种算法对测试函数f3 迭代过程对比图Fig.5 Comparison Diagram of Three Algorithms on the Iterative Process of Test Function f3

从表4 中可以发现，处理复杂非线性函数时DAFSA 的计算精度优于AFSA 和DE，但DAFSA 求解时间大于DE。从图4、图5中的迭代对比图可以看出DAFSA 相对于AFSA 陷入局部最优的时间明显缩短，早熟现象得到改善，在迭代后期仍朝着最优解方向前进，且寻优结果明显优于AFSA；DAFSA 结果稳定性明显优于DE，且DE 在后期迭代相对停止。

测试函数f5的结果显示，DE 的精度要高于DAFSA，但其处理其他测试函数时，随机性、不稳定性和精度不足现象比较明显，DAFSA 在处理测试函数时展示出的稳定性要明显优于其他算法，且其精度基本达到0.0001，符合工程使用要求。因此测试结果证实了DAFSA 在计算准确性和稳定性、计算效率方面的优势。

4 工程应用

为验证提出的DAFSA 算法实用性，以50t/22.5m 桥式起重机主梁金属结构为研究对象，对其进行轻量化设计。

箱型桥架作为桥式起重机的主要承载构件，它的设计参数取值优劣决定了整个起重机的设计成败。因其受力情况复杂和篇幅原因，仅考虑其承受自重均布载荷q=ρA（A 为净截面面积）和集中载荷，构建主梁的结构力学模型，如图6 所示。

图6 主梁力学模型简图Fig.6 Schematic Diagram of Mechanical Model of Main Girder

定义结构设计变量为：x1（上下翼缘板厚度），x2（主腹板厚度），x3（副腹板厚度），x4（腹板间距），x5（腹板高度）。

箱型梁截面几何约束条件为：

强度约束条件为：

式中：M—最危险截面承受的弯矩；y—截面形心与危险点的垂直距离；Ix—箱型梁截面惯性矩[14]；［σ］—许用应力，［σ］=235/1.48=158.78MPa。

刚度约束条件为：

式中：Yc—集中载荷在跨中时主梁最大变形[14]；［Y］—结构许用静位移，［Y］=L/500。

优化设计目标为在满足结构强度、刚度约束条件下，结构重量最小，具体表达为截面面积最小，即A 值最小。主梁参数源自文献[15]，如表 5 所示。

表5 箱型梁工作参数Tab.5 Operating Parameters of Box Girder

DAFSA 算法在 MATLAB 中运行，参数设置：fishnums=100；MAXGEN=1000；delta=0.6；try_number=1；Step=7；Visual=5。运行结果（圆整后），如表6 所示。经代入检验，圆整后的结果满足几何约束条件、强度、刚度条件。通过与参考文献[15]中的数据对比，优化后截面面积减小5.2%，由此可得出如下结论：采用DAFSA 算法，在满足几何约束条件及强度、刚度约束的条件下，获得了优化的箱型主梁结构。

表6 箱型梁优化结果Tab.6 Optimization Results of Box Girder

5 结论

（1）算法收敛精度、稳定性以及结果精度在桥式起重机轻量化设计中具有重要作用，而现有算法在参数之间相互关系及早熟现象尚未涉及。针对该问题，提出一种基于嵌入机制的改进人工鱼群算法。（2）基于嵌入机制的改进人工鱼群算法是以参数统计分析为基础，设定步长与视野数值成反比的条件下，构建一种模仿生物视觉特性的步长、视野因子模型，并将差分进化算法中的变异行为作为人工鱼群完成觅食、聚群、追尾行为后的干扰行为。经测试函数分析结果表明DAFSA 在稳定性、计算精度与早熟现象改进方面较AFSA 有明显提升。（3）将上述模型及方法应用在50t/22.5m 桥式起重机主梁金属结构轻量化设计中，结果表明在给定约束条件范围下，对各变量进行合理赋值，最优解的计算精度较高，从而验证了DAFSA 算法的实用性。