径向基神经网络模型的白车身轻量化设计

张功学，牛顾根，王德雨，郭珊珊

（陕西科技大学机电工程学院，陕西 西安 710021）

1 引言

车身作为整车的重要组成部分，其质量影响着整车的制造成本，燃油性能以及制动安全性，对于轿车白车身轻量化研究一直是学术界的热点话题。前人对车身轻量化研究主要采用有限元法和实车试验法对车身结构优化设计[1-3]。通过试验得到的结果准信度高，但花费了大量人力和经费，其效率低下成为新车研发的主要问题，在此种情况下，有限元法和试验法相结合显得尤为重要。在车身优化问题上，文献[4]采用隐式全参化建模，对白车身进行多目标优化；文献[5]运用Radioss 求解器分析白车身刚度的分布情况，改进车身结构件；文献[6]采用灵敏度分析法对白车身实现了降重。

国内外学者[7-9]通过建立近似模型代替工程实际中复杂的多自由度模型，计算效率得到了明显的提升。文献[10]采用一阶响应面模型，以非支配排序遗传算法对白车身进行多目标优化；文献[11]通过研究耐撞性能，改变结构来降低车身质量并分别建立了克里金模型和响应面模型。径向基神经网络模型是以函数逼近理论为基础构造的一类前向局部逼近模型。其优点为函数逼近能力、模式识别能力强，精确度高。但其在汽车领域应用少，考虑到车身结构复杂，分析时间长，为了得到较为准确的优化解，以朗逸230TSI 款轿车白车身为研究对象，采用有限元法建立径向基神经网络模型，对白车身进行了轻量化设计。

2 白车身有限元模型

采用Hypermesh 对白车身进行前处理。考虑到白车身零件数量多，结构复杂，为了高效准确的得到分析结果需要对车身进行合理的简化。在简化过程中，以符合主要力学特性为根本，使每个单元与实际结构保持一致，且单元传递的力学特性与实际一致。通过模型简化，网格划分，得到白车身有限元模型，如图1 所示。全车身共有4778 个焊点，356616 个节点，350259 个壳单元。

图1 白车身有限元模型Fig.1 Body in White Finite Element Model

3 刚度分析

3.1 扭转刚度分析

车身扭转刚度用来衡量车身抵抗扭转变形的能力，假设将白车身视为刚度均匀的杆件，则白车身扭转刚度可表示为：

式中：GJ—扭转刚度（N·m2/deg）；T—扭矩（N·m）；L—轴长（m）；θ—轴间相对扭转角（deg）。

扭转角公式为：

通过约束后悬架支撑点和前防撞梁中间部位X、Y、Z 三方向平动自由度，在左右前悬架支撑点施加等大反向载荷，扭矩为5500N·m，为了防止个别节点承力突增，采用REB3 单元将力均分在周围节点处。为了观察车身各部分受力的变形情况，在车身车门两侧下方对称取了20 个观测点。观测点位置分布，如图2 所示。

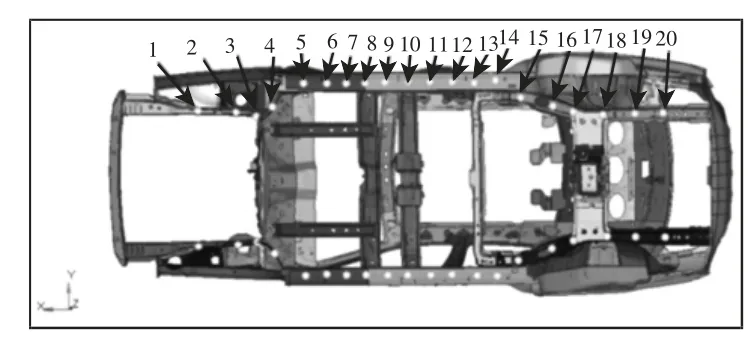
图2 观测点位置分布图Fig.2 Location Map of Observation Points

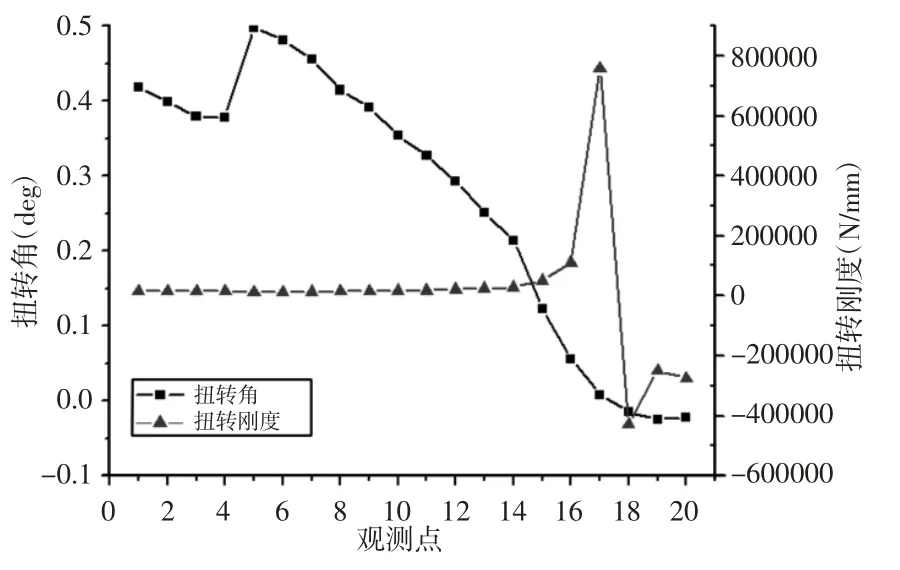
图3 沿车身纵向转角及扭转刚度变化Fig.3 Variations in Longitudinal Angle and Torsional Stiffness Along the Body

为了便于观察车身纵向转角和扭转刚度的变化，绘制了观测点转角及扭转刚度变化，如图3 所示。由图知该车身纵向变形整体上比较平滑，最大变形位置发生在观测点5 处，此处为前围板以及后悬架支撑点附近，出现这种情况与经验发生区域相吻合。对于车身扭转工况下刚度的好坏，主要以扭转刚度进行评价。根据所选车型参数，左右前悬架安装支点间距为1.125m，通过定点测量车前轴两侧位移形变的绝对值分别为5.343mm、6.249mm。将数据带入式（1）、式（2），得到了扭转角为 0.5904deg 和扭转刚度为10480N·m2/deg。该车型扭转刚度允许值为10000N·m2/deg，故该车符合设计要求。

3.2 弯曲刚度分析

车身的弯曲刚度是一个表示车身挠度的量。车身受力复杂，为准确高效描述车身弯曲刚度，通常采用以下公式定义：

式中：Ω—车身弯曲刚度（N/mm）；∑F—车身弯曲的集中载荷（N）；δZmax—门槛或纵梁的最大弯曲挠度（mm）。

通过约束前后支撑点Y、Z 方向及后支撑点X 方向平动自由度。在前后座椅安装处施加左右对称垂直向下的力，大小F=1600N。在Hyperview 后处理软件里，分别测得各个观测点在Z 方向的位移变化量，绘制观测点弯曲挠度变化，如图4 所示。由图知大部分挠度分布比较平滑，说明弯曲刚度分布比较均匀，在观测点15 处挠度变化取得最大值，此处为门槛梁后端，说明此处为弯曲刚度的薄弱位置。

图4 观测点弯曲挠度变化图Fig.4 Observed Point Bending Deflection Change Diagram

在Hyperview 后处理软件中，提取门槛梁后端最大挠度变形值为0.5456mm，带入式（3）得到车身最小弯曲刚度为11730N/mm。该车型弯曲刚度设计值范围为（11000～13000）N/mm，故该车满足设计要求。

4 模态分析

模态反映的是物体的固有动态属性，对车身进行模态分析的最终目的是得到相应的模态参数和振型，为后期车身优化设计做准备，可以避免汽车在使用过程中产生共振，起到降低噪声，提高乘客舒适度的作用。

车身属于连续体，质量和弹性是连续分布的，在进行振动分析时对其进行离散化处理，理论上可以得到无穷多阶模态。因结构的振动特性主要由低阶模态决定，故在EIGRL 卡片中设置频率范围为（0～50）Hz，默认跳过刚体模态，计算在此范围内的所有模态频率和振型。由于结构的固有频率与外力无关，通过释放车身全部载荷和约束，得到了10 阶频率和振型，如表1 所示。

为了进一步验证有限元模型准确性，为后续优化设计做准备，对白车身进行了模态试验。试验采用自由模态方式，用4 根质量小柔性好的皮绳将白车身固定在试验架上，模拟车身自由状态，且整个悬挂系统固有频率不大于2Hz。激振器固定在刚度大的车头位置（车身前横梁处），整车身布置106 个测振点。试验随机信号由汽车振动噪声分析系统产生，并将激励信号和响应信号数据输送给计算机，利用Onosokki DS-3000 数据分析系统处理信号，EDM Modal 软件识别模态参数。模态试验系统，如图5 所示。经数据处理得到模态试验数据，如表1 所示。

图5 模态试验系统图Fig.5 Modal Test System Diagram

表1 有限元仿真与模态试验结果对比 单位：HzTab.1 Comparison of Finite Element Simulation and Modal Test Results

由表1 知，仿真模态与试验模态阶次上一一对应，从振型上看有较好的相关性，仿真值与试验值存在一定误差，一方面车身并非是完全处于自由状态，只是接近自由状态，另一方面是对模型进行前处理上，如倒角，工艺孔和焊点的处理等。误差在10%以内，考虑以上因素，说明仿真结果具有参考价值，有限元模型的准确性得到了验证。该车身一阶频率为21.62Hz，根据文献[12]汽车在150km/h 速度以下行驶，车身受路面不平度的激励在20Hz 以下，因此车身一阶固有频率高于路面激励，避免了与路面激励共振。车身一阶扭转频率（第2 阶模态）为25.45Hz，与发动机怠速运转频率较接近，因此需要优化提高一阶扭转频率，防止其与发动机怠速运转频率发生共振。

5 白车身结构优化

5.1 选取设计变量

车身零件数量较多，如果把所有零件都设计为变量，计算工作量巨大，甚至参数会得不到最优解。Plackett-Burman 试验设计法针对变量数目多，能高效筛选出变量对响应的灵敏程度，因此本次研究采用此方法对车身35 个主要零部件进行了筛选，得到了包括左前纵梁槽型板在内的18 个结构件，并以18 个构件的厚度作为设计变量，部分构件见表3 第1 列。

5.2 建立径向基神经网络模型

径向基神经网络模型是以待测点与样本点之间的欧几里德范数为自变量，以径向函数为基函数，通过线性叠加构造径向基函数模型，具有很强的逼近复杂非线性能力。模型从输入到输出的映射关系为：

式中：x—输入矢量；φ—基函数；w—权系数；ck—第K 个节点的中心；σk—第K 个节点的基宽度参数。

根据式（4）、式（5）的映射关系，采用哈默斯雷设计法对18个构件变量进行样本采集，以设计变量的原始数值的30%作为上下限。以哈默斯雷试验设计选取的样本点为输入矩阵，拟合了白车身的18 个设计变量与7 个响应的近似关系，作为白车身的径向基神经网络模型。响应1～响应7 分别为车身质量、弯曲工况下左门槛最大位移点的Z 向位移、弯曲工况下右门槛最大位移点的Z 向位移、扭转工况前轴左侧测量点的位移值、扭转工况前轴右侧测量点的位移值、第7 阶模态和第8 阶模态。由于篇幅有限，仅给出响应1，响应3 的模型。部分径向基神经网络模型，如图6 所示。

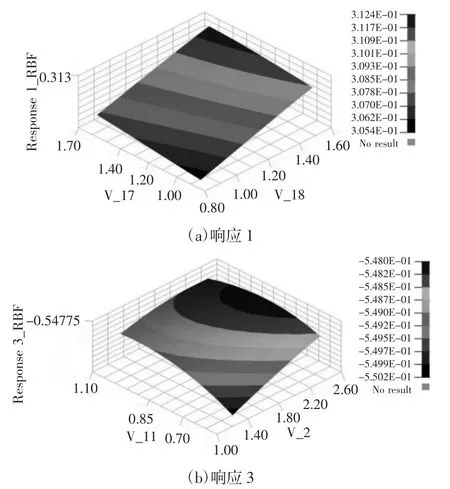
图6 部分径向基神经网络模型Fig.6 Partial Radial Basis Neural Network Model

车身是一个复杂的系统，直接对系统进行优化设计，实现系统之间的数据交换和融合计算量大，时间周期长。通过建立车身的近似模型代替原有限元模型可以对此类问题进行有效的规避，提高工作效率。近似模型准确性是后期优化结果的关键，因此有必要对建立的近似模型进行验证。采用复相关系数R2、平均相对误差RAAE 和均方根差RMSE 来评价模型精度，通过提取检验矩阵样本点得到近似模型检验表，如表2 所示。

表2 检验矩阵样本点相应误差统计Tab.2 Corresponding Error Statistics of Test Matrix Sample Points

根据评定标准R2的值越接近1，RAAE 和RMSE 的值越小，表示拟合的近似模型精度越好，通常认为R2值大于0.9 就表示近似模型与实际模型足够逼近。由表2 知，该模型的R2值均大于0.97，说明径向基神经网络模型足够精确。

5.3 白车身多目标优化

通过对车身扭转刚度、弯曲刚度和模态进行分析知，车身一阶扭转频率接近发动机怠速运转频率，容易发生共振，需要对其进行优化设计，以提高其固有频率。故将车身质量，一阶扭转频率（第2 阶固有频率）作为优化目标，将扭转刚度N、弯曲刚度W 和第1 阶模态频率作为约束条件，在满足不低于刚度设计值的情况下对车身进行多目标优化。优化数学模型建立如下：

式中：ti—设计变量；tia、tib—设计变量的上、下限。

图7 车身质量与一阶扭转频率Pareto 前沿面图Fig.7 Pareto Frontier View of Body Mass and First-Order Torsional Frequency

设置种群大小为174，进化终止代数为（20～50），变异率为0.01，交叉率为0.4 利用多目标遗传算法对拟合的近似模型进行优化设计，经过7800 多次迭代，得到模型的148 组最优解，其Pareto 前沿面，如图6 所示。五角星表示优化的推荐最优解。限于篇幅问题仅列出部分优化后设计变量值，如表3 所示。

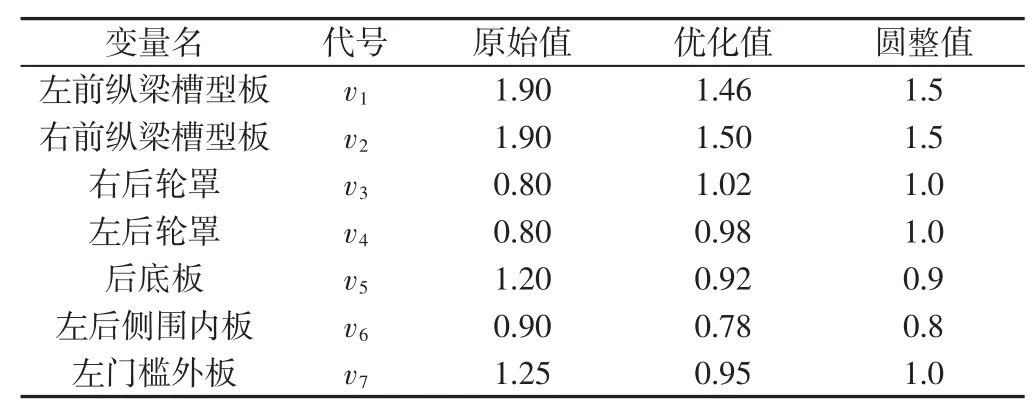
表3 优化后部分变量值 单位：mmTab.3 Optimized Partial Variable Values

5.4 优化结果

通过建立径向基神经网络模型对白车身进行多目标优化，由于是近似模型，需要对优化后结果准确性进行验证。将最优方案圆整后尺寸带入有限元模型，通过比较知，近似模型与有限元模型误差小于等于3.13%，在误差范围内验证了近似模型的准确性，说明优化结果准确。通过优化后结果对比表4 知，优化后的质量减轻了18.3kg，第2 阶固有频率提高了5.24Hz，达到了轻量化目的。

表4 优化后结果对比Tab.4 Comparison of Results After Optimization

6 结论

（1）以朗逸230TSI 款轿车白车身为研究对象，对其进行扭转刚度、弯曲刚度和模态分析。结果表明，车身扭转刚度为10480N·m2/deg，弯曲刚度为11730N/mm 均满足设计要求；但车身一阶扭转频率较低，需对其进行优化。（2）建立径向基神经网络模型，对白车身进行多目标优化，得到最优方案。通过近似模型和优化方案比较验证了径向基神经网络模型的准确性。优化结果显示，在弯曲刚度，扭转刚度，1 阶固有频率不降低的情况下，车身减重18.3kg，一阶扭转频率提升了5.24Hz。径向基神经网络模型的优化方法，准确高效，可推广到汽车其他部件设计。